Secure Computation Lecture 17 18 Arpita Patra Recap

Secure Computation Lecture 17 -18 Arpita Patra

Recap >> i. t (perfect) MPC in malicious Setting >Three orthogonal problems- (n, t)-sharing, reconstruction, multiplication protocol > Verifiable Secret Sharing (VSS) will take care first two problems >> Verifiable Secret Sharing (VSS) > Definition (Secrecy, Correctness, Strong Commitment) > Properties of Bivariate polynomial > Six round construction based on bivariate poly with n > 3 t > Four round construction with minor tweaks > Reconstruction from error correction of RS codes- will be discussed today

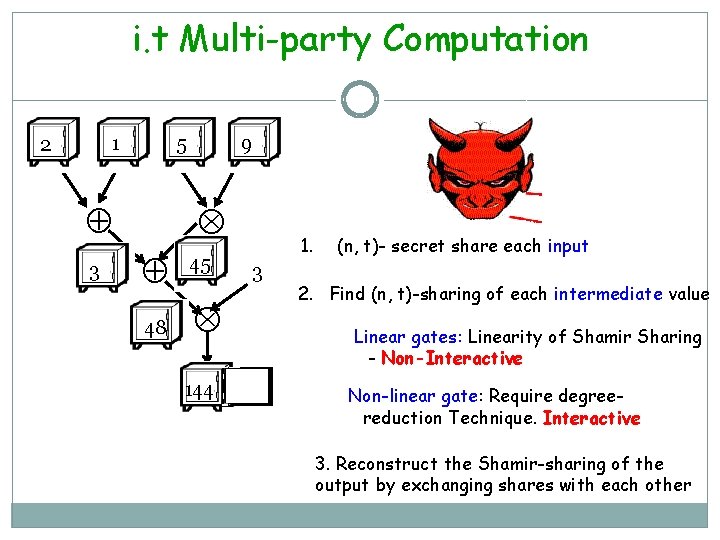
i. t Multi-party Computation [BGW] 1 2 5 3 9 45 48 144 1. 3 (n, t)- secret share each input 2. Find (n, t)-sharing of each intermediate value Linear gates: Linearity of Shamir Sharing - Non-Interactive Non-linear gate: Require degreereduction Technique. Interactive 3. Reconstruct the Shamir-sharing of the output by exchanging shares with each other

Definition of VSS [CGMA 85] Extends Secret Sharing to the case of malicious corruption Secret s Dealer s is committed secure Sharing Phase v 1 v 2 v 3 … vn Reconstruction Phase Secret s

Definition of VSS [CGMA 85] Continued. . q n parties P = {P 1, …, Pn}, dealer D (e. g. , D = P 1) q t corrupted parties (possibly including D) At Secrecy – If D is honest, then At has no information about secret s during the Sharing phase Correctness – If D is honest, then secret s will be correctly reconstructed during reconstruction phase Strong Commitment – Corrupted D commits a unique s* - s* should be uniquely reconstructed

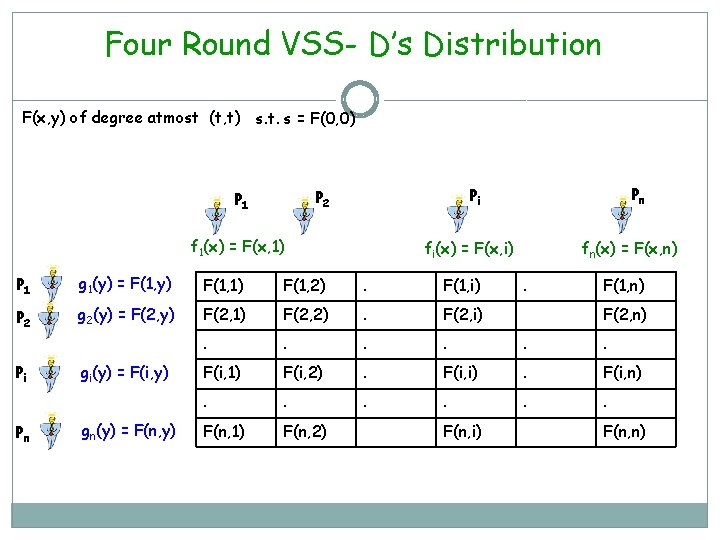
Bivariate Polynomial and its properties F(x, y) of degree atmost (t, t) f 1(x) = F(x, 1) fi(x) = F(x, i) fn(x) = F(x, n) g 1(y) = F(1, y) F(1, 1) F(1, 2) . F(1, i) g 2(y) = F(2, y) F(2, 1) F(2, 2) . F(2, i) . . . F(i, 1) F(i, 2) . F(i, i) . F(i, n) . . . F(n, 1) F(n, 2) gi(y) = F(i, y) gn(y) = F(n, y) F(n, i) Claim 1: t F(x, i)’s and t F(i, y)’s will leak NO info about F(0, 0). Claim 2: (t+1) F(x, i)’s or (t+1) F(i, y)’s completely determine F(x, y). Claim 3: gi(j) = fj(i) = F(i, j) and gj(i) = fi(j) = F(j, i) . F(1, n) F(2, n) F(n, n)

Four Round VSS- D’s Distribution F(x, y) of degree atmost (t, t) s. t. s = F(0, 0) Pn Pi P 2 P 1 f 1(x) = F(x, 1) fi(x) = F(x, i) fn(x) = F(x, n) P 1 g 1(y) = F(1, y) F(1, 1) F(1, 2) . F(1, i) P 2 g 2(y) = F(2, y) F(2, 1) F(2, 2) . F(2, i) . . . F(i, 1) F(i, 2) . F(i, i) . F(i, n) . . . F(n, 1) F(n, 2) Pi Pn gi(y) = F(i, y) gn(y) = F(n, y) F(n, i) . F(1, n) F(2, n) F(n, n)

Four Round VSS- Verification, Complaint & Resolution Pj Pi fj(x) = F(x, j) gj(y) = F(j, y) fi(x) = F(x, i) gi(y) = F(i, y) fi(j) = g j(i) = F(j, i) gi(j) = fj(i) = F(i, j) Every pair of honest parties’ polynomials are pairwise consistent

Four Round VSS- Output share Note: D can choose the polynomial with which it wants to (n, t)-share its secret as f(x) and then choose F(x, y) such that F(x, 0) = f(x) and then do VSS using F(x, y) f 0(0) = F(0, 0) = s f 0(x) = F(x, 0) P 1 g 1(0) = F(1, 0) gi(1) P 2 g 2(0) = F(2, 0) gi(2) = f 2(i) Pi gi(0) = F(i, 0) gi(i) = fi(i) Pn gn(0) = F(n, 0) gi(n) = fn(i) = f 1(i) Two level sharing- each Shamir share is also Shamir-shared

Reconstruction Phase (Error Correction of Reed-Solomon Codes) P 1 f(1) (n, t+1)-RS code (over field F, |F| > n): P 2 f(2) Encoding: Given a message block of t+1 field elements, m 0, m 1, …mt , define f(x) = m 0 + m 0 x + ……+ mt xt C = (f(1), f(2), …. , f(n)) Pi f(i) Distance d of (n, t+1)-RS code is: n-t Theorem: (n, t+1) RS code can correct x errors if d > 2 x Pn f(n) With n > =3 t+1, d > 2 t, so we can correct t errors

Berlekamp-Welch Error Correction Algorithm for RS Codes P 1 f(1) r(x): Polynomial defined by the broadcasted points (degree at most 3 t) P 2 f(2) f(x): Actual Polynomial (degree at most t). Goal is to find this poly e(x): Error polynomial (x-e 1)(x-e 2)…. (x-et) : e 1 , e 2, … et from {1, . . , n} (degree t) f(x)e(x) = r(x)e(x) at x = 1, 2…. . n Pi f(i) Let f(x)e(x) = q(x) (degree 2 t) q(x) = r(x)e(x) at x = 1, 2…. . n Find f(x) = Find e(x) Pn f(n) Not claiming the LHS and RHS polynomials are same. They are same at x= 1, 2…. . n q(x) and e(x) are unknown How to find e(x)? - Solving system of linear equations Unknowns: Coefficients of q(x) and e(x) 3 t+1 Equations: 3 t+1 solving system of linear equations reduces to (publicly known) matrix multiplication

Distributed Error Correction of RS Codes P 1 f(1) P 2 f(2) f(1) Pi f(2) f(i) linear operations Co-eff of e(x) Pn f(n)

i. t Multi-party Computation 1 2 5 3 9 45 48 144 1. 3 (n, t)- secret share each input 2. Find (n, t)-sharing of each intermediate value Linear gates: Linearity of Shamir Sharing - Non-Interactive Non-linear gate: Require degreereduction Technique. Interactive 3. Reconstruct the Shamir-sharing of the output by exchanging shares with each other

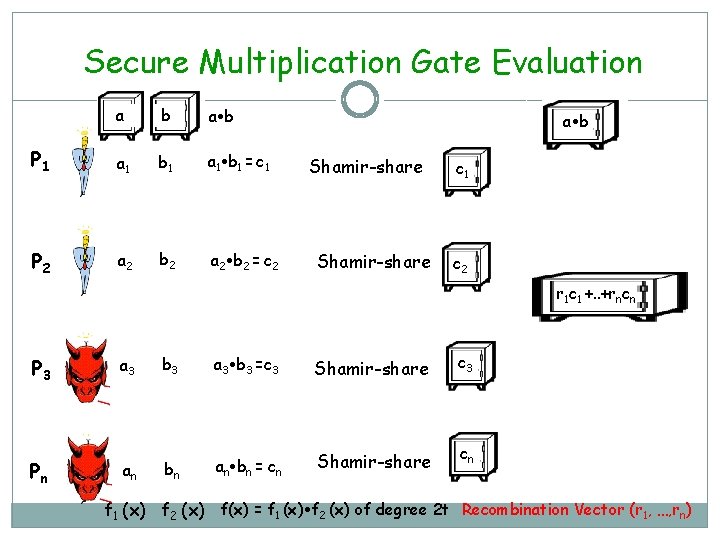
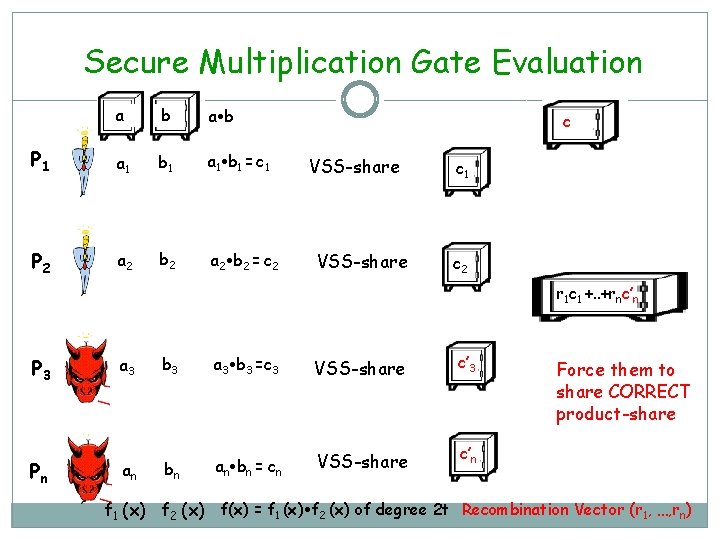
Secure Multiplication Gate Evaluation a b P 1 a 1 b 1 = c 1 P 2 a 2 b 2 = c 2 where Recombination Vector (r 1, …, rn) P 3 a 3 b 3 =c 3 Pn an bn = cn f 1 (x) f 2 (x) f(x) = f 1 (x) f 2 (x) of degree 2 t

Secure Multiplication Gate Evaluation a b P 1 a 1 b 1 = c 1 P 2 a 2 b 2 = c 2 a b Shamir-share c 1 c 2 r 1 c 1 +. . +rncn P 3 Pn a 3 an b 3 a 3 b 3 =c 3 Shamir-share c 3 bn an bn = cn Shamir-share cn f 1 (x) f 2 (x) f(x) = f 1 (x) f 2 (x) of degree 2 t Recombination Vector (r 1, …, rn)

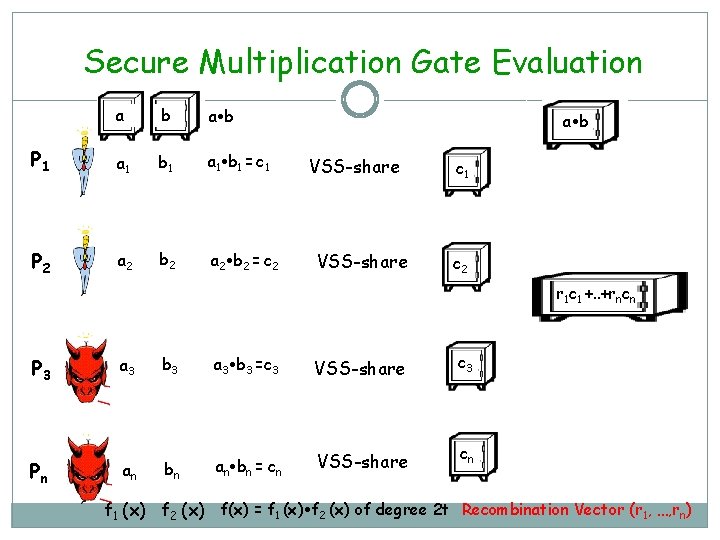
Secure Multiplication Gate Evaluation a b P 1 a 1 b 1 = c 1 P 2 a 2 b 2 = c 2 a b VSS-share c 1 c 2 r 1 c 1 +. . +rncn P 3 Pn a 3 an b 3 a 3 b 3 =c 3 VSS-share c 3 bn an bn = cn VSS-share cn f 1 (x) f 2 (x) f(x) = f 1 (x) f 2 (x) of degree 2 t Recombination Vector (r 1, …, rn)

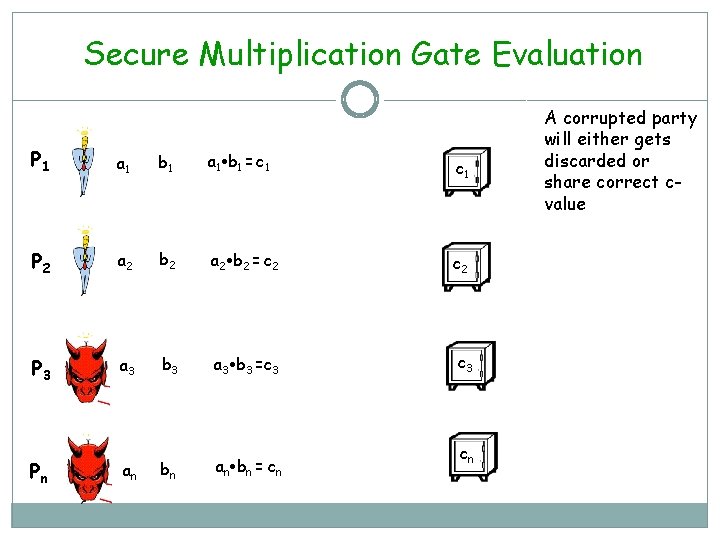
Secure Multiplication Gate Evaluation a b P 1 a 1 b 1 = c 1 P 2 a 2 b 2 = c 2 c VSS-share c 1 c 2 r 1 c 1 +. . +rnc’n P 3 Pn a 3 an b 3 a 3 b 3 =c 3 VSS-share c’ 3 bn an bn = cn VSS-share c’n Force them to share CORRECT product-share f 1 (x) f 2 (x) f(x) = f 1 (x) f 2 (x) of degree 2 t Recombination Vector (r 1, …, rn)

Secure Multiplication Gate Evaluation P 1 a 1 b 1 = c 1 P 2 a 2 b 2 = c 2 P 3 a 3 b 3 =c 3 bn an bn = cn Pn an cn A corrupted party will either gets discarded or share correct cvalue

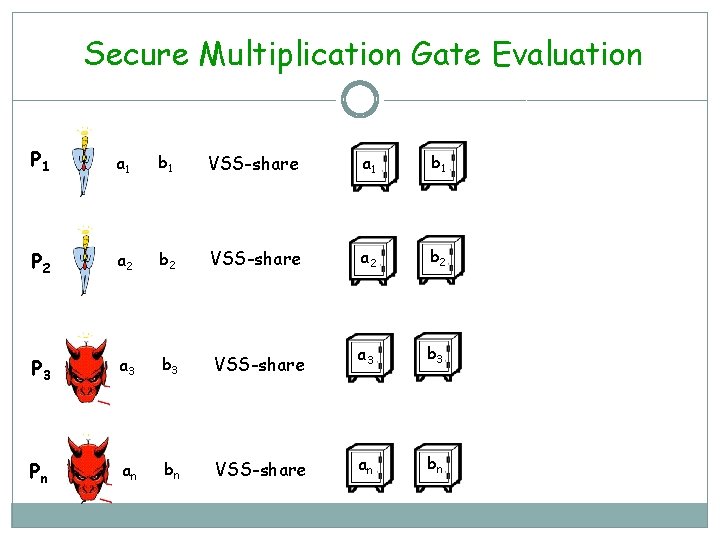
Secure Multiplication Gate Evaluation P 1 a 1 b 1 VSS-share a 1 b 1 P 2 a 2 b 2 VSS-share a 2 b 2 P 3 a 3 b 3 VSS-share a 3 b 3 Pn an bn VSS-share an bn

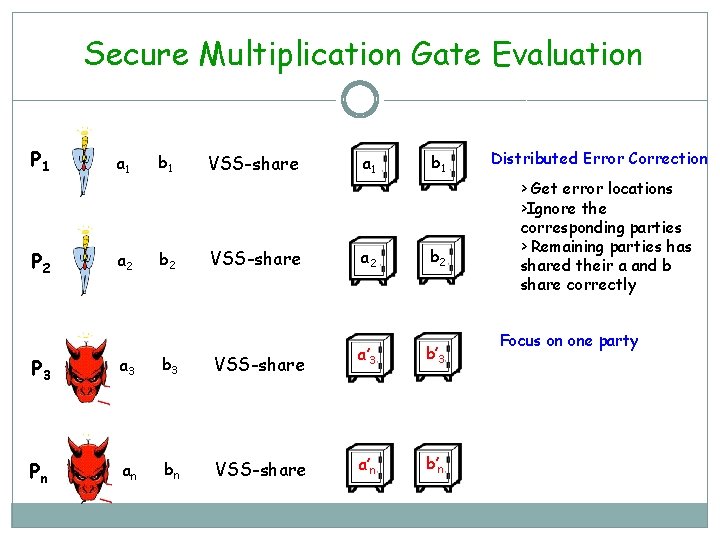
Secure Multiplication Gate Evaluation P 1 P 2 a 1 a 2 b 1 b 2 VSS-share P 3 a 3 b 3 VSS-share Pn an bn VSS-share a 1 b 1 a 2 b 2 a’ 3 b’ 3 a’n b’n Distributed Error Correction > Get error locations >Ignore the corresponding parties > Remaining parties has shared their a and b share correctly Focus on one party

Secure Multiplication Gate Evaluation (abusing notation) P a b A(x) B(x) a 1 b 1 C(x) = A(x)B(x) - 2 t-degree - Non-random How to reduce the degree and randomize the polynomial? Choose t random polynomials D 1(x), …, Dt(x) s. t. the following polynomial is random and at most degree-t poly with constant term c = ab a 2 b 2 D(x) = C(x) - x. D 1(x) -…. -xt Dt(x) C(x) = c + c 1 x + ……ct xt + ct+1 xt+1 +………. + c 2 t-1 x 2 t-1 + c 2 t x 2 t Dt(x) = a 3 b 3 an bn rt, 1 + rt, 2 x + ………+ rt, t-1 xt-1 + c 2 t xt c

Secure Multiplication Gate Evaluation P a b A(x) B(x) a 1 b 1 C(x) = A(x)B(x) - 2 t-degree - Non-random How to reduce the degree and randomize the polynomial? Choose t random polynomials D 1(x), …, Dt(x) s. t. the following polynomial is random and at most degree-t poly with constant term c = ab a 2 b 2 D(x) = C(x) - x. D 1(x) -…. -xt Dt(x) C(x) = c + c 1 x + ……ct xt + ct+1 xt+1 +………. + c 2 t-1 x 2 t-1 + c 2 t xt Dt(x) = a 3 b 3 an bn Dt-1(x) = rt, 1 xt + rt, 2 xt+1 + ………+ rt, t-1 xt-1 + c 2 t x 2 t rt-1, 1 + rt-1, 2 x + ……… + (c 2 t-1 – rt, t-1)xt c

Secure Multiplication Gate Evaluation P a b A(x) B(x) a 1 b 1 C(x) = A(x)B(x) - 2 t-degree - Non-random How to reduce the degree and randomize the polynomial? Choose t random polynomials D 1(x), …, Dt(x) s. t. the following polynomial is random and at most degree-t poly with constant term c = ab a 2 b 2 D(x) = C(x) - x. D 1(x) -…. -xt Dt(x) C(x) = c + c 1 x + ……ct xt + ct+1 xt+1 +………. + c 2 t-1 x 2 t-1 + c 2 t xt Dt(x) = a 3 b 3 an bn xt-1 Dt-1(x)= rt, 1 xt + rt, 2 xt+1 + ………+ rt, t-1 xt-1 + c 2 t x 2 t rt-1, 1 xt-1 + rt-1, 2 xt + ……… + (c 2 t-1 – rt, t-1) xt-1 c

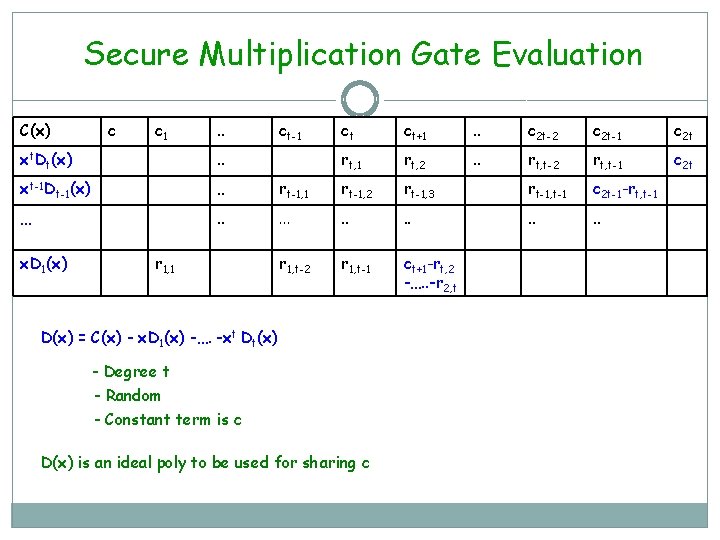
Secure Multiplication Gate Evaluation C(x) c c 1 . . ct-1 ct ct+1 . . c 2 t-2 c 2 t-1 c 2 t rt, 1 rt, 2 . . rt, t-2 rt, t-1 c 2 t xt. Dt(x) . . xt-1 Dt-1(x) . . rt-1, 1 rt-1, 2 rt-1, 3 rt-1, t-1 c 2 t-1 -rt, t-1 … . . r 1, t-2 r 1, t-1 ct+1 -rt, 2 -…. . -r 2, t x. D 1(x) r 1, 1 D(x) = C(x) - x. D 1(x) -…. -xt Dt(x) - Degree t - Random - Constant term is c D(x) is an ideal poly to be used for sharing c

Secure Multiplication Gate Evaluation P a (using VSS; and setting F(x, 0)) b A(x) B(x) D 1(x) D 2(x) Dt(x) C(x) D(x) ? = C(x) - x. D 1(x) -…. -xt Dt(x) a 1 b 1 d 11 d 21 dt 1 a 1 b 1 d 1 ? = a 1 b 1 – 1. d 11 - …. - 1 t dt 1 a 2 b 2 d 12 d 22 dt 2 a 2 b 2 d 2 ? = a 2 b 2 – 2. d 12 - …. -2 t dt 2 a 3 b 3 d 13 d 23 dt 3 a 3 b 3 d 3 ? = a 3 b 3 – 3. d 13 - …. -3 t dt 3 an bn dn d 1 n d 2 n dtn anbn dn ? = anbn – n. d 1 n - …. - nt dtn If P is honest we are done, since D(x) is at most degree-t poly and random

Secure Multiplication Gate Evaluation P P 3 complains, check if complaint is correct, if so discard P, else ignore the complaint. a b A(x) B(x) D 1(x) D 2(x) D(x) is degree t but RHS may not be may not share c. degree t but shares c Dt(x) C(x) D(x) ? = C(x) - x. D 1(x) -…. -xt Dt(x) a 1 b 1 d 11 d 21 dt 1 a 1 b 1 d 1 ? = a 1 b 1 – 1. d 11 - …. - 1 t dt 1 a 2 b 2 d 12 d 22 dt 2 a 2 b 2 d 2 ? = a 2 b 2 – 2. d 12 - …. -2 t dt 2 a 3 b 3 d 13 d 23 dt 3 a 3 b 3 d 3 ? = a 3 b 3 – 3. d 13 - …. -3 t dt 3 an bn dn d 1 n d 2 n dtn anbn dn ? = anbn – n. d 1 n - …. - nt dtn If all honest parties find the relation true, then D(x) shares c. But we do not know who is honest/corrupted

Chalk & Talks CT 4 [LR 15]: Blazing Fast 2 PC in the Offline/Online Setting with Security for Malicious Adversaries. https: //eprint. iacr. org/2015/987. pdf CT 5 [AMPR 15]: Non-Interactive Secure Computation Based on Cut-and. Choose. http: //eprint. iacr. org/2015/282 CT 6 [IOZ 15]: Secure Multi-Party Computation with Identifiable Abort; http: //eprint. iacr. org/2015/325 CT 7 [LPSY 15]: Efficient Constant Round Multi-party Computation Combining BMR and SPDZ. https: //eprint. iacr. org/2015/523 CT 8 [HR 14]: Multi-Valued Byzantine Broadcast: the t < n Case http: //eprint. iacr. org/2013/553