Scheduling under Uncertainty Frank Werner Faculty of Mathematics

Scheduling under Uncertainty Frank Werner Faculty of Mathematics

Outline of the talk 1. 2. 3. 4. 5. 6. Introduction Stochastic approach Fuzzy approach Robust approach Stability approach Selection of a suitable approach PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 2

1. Introduction Notations PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 3

• Deterministic models: all data are deterministically given in advance • Stochastic models: data include random variables In real-life scheduling: many types of uncertainty (e. g. processing times not exactly known, machine breakdowns, additionally ariving jobs with high priorities, rounding errors, etc. ) Uncertain (interval) processing times: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 4

Relationship between stochastic and uncertain problems: Distribution function Density function PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 5

Approaches for problems with inaccurate data: • Stochastic approach: use of random variables with known probability distributions • Fuzzy approach: fuzzy numbers as data • Robust approach: determination of a schedule hedging against the worst-case scenario • Stability approach: combination of a stability analysis, a multi-stage decision framework and the concept of a minimal dominant set of semi-active schedules → There is no unique method for all types of uncertainties. PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 6

Two-phase decision-making procedure 1) Off-line (proactive) phase construction of a set of potentially optimal solutions before the realization of the activities (static scheduling environment, schedule planning phase) 2) On-line (reactive) phase selection of a solution from when more information is available and/or a part of the schedule has already been realized → use of fast algorithms (dynamic scheduling environment, schedule execution phase) PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 7

General literature (surveys) Pinedo: Scheduling, Theory, Algorithms and Systems, Prentice Hall, 1995, 2002, 2008, 2012 • Slowinski and Hapke: Scheduling under Fuzziness, Physica, 1999 • Kasperski: Discrete Optimization with Interval Data, Springer, 2008 • Sotskov, Sotskova, Lai and Werner: Scheduling under Uncertainty; Theory and Algorithms, Belarusian Science, 2010 • For the RCPSP under uncertainty, see e. g. • Herroelen and Leus, Int. J. Prod. Res. . 2004 • Herroelen and Leus, EJOR, 2005 • Demeulemeester and Herroelen, Special Issue, J. Scheduling, 2007 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 8

2. Stochastic approach • Distribution of random variables (e. g. processing times, release dates, due dates) known in advance • Often: minimization of expectation values (of makespan, total completion time, etc. ) Classes of policies (see Pinedo 1995) • Non-preemptive static list policy (NSL) • Preemptive static list policy (PSL) • Non-preemptive dynamic policy (ND) • Preemptive dynamic policy (PD) PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 9

Some results for single-stage problems (see Pinedo 1995) Single machine problems (a) Problem WSEPT rule: order the jobs according to non-increasing ratios Theorem 1: The WSEPT rule determines an optimal solution in the class of NSL as well as ND policies. (b) Problem Theorem 2: The EDD rule determines an optimal solution in the class of NSL, ND and PD policies. PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 10

(c) Problem Theorem 3: The WSEPT rule determines an optimal solution in the class of NSL, ND and PD policies. Remark: The same result holds for geometrically distributed Parallel machine problems (a) Problem Theorem 4: The LEPT rule determines an optimal solution in the class of NSL policies. PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 11

(b) Problem Theorem 5: The non-preemptive LEPT policy determines an optimal solution in the class of PD policies. (c) Problem Theorem 6: The non-preemptive SEPT policy determines an optimal solution in the class of PD policies. PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 12

Selected references (1) • • • • Pinedo and Weiss, Nav. Res. Log. Quart. , 1979 Glazebrook, J. Appl. Prob. , 1979 Weiss and Pinedo, J. Appl. Prob. , 1980 Weber, J. Appl. Prob. , 1982 Pinedo, Oper. Res. , 1982; 1983 Pinedo, EJOR, 1984 Pinedo and Weiss, Oper. Res. , 1984 Möhring, Radermacher and Weiss, ZOR, 1984; 1985 Pinedo, Management Sci. , 1985 Wie and Pinedo, Math. Oper. Res. , 1986 Weber, Varaiya and Walrand, J. Appl. Prob. , 1986 Righter, System and Control Letters, 1988 Weiss, Ann. Oper. Res. , 1990 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 13

Selected references (2) • • • • Weiss, Math. Oper. Res. , 1992 Righter, Stochastic Orders, 1994 Cai and Tu, Nav. Res. Log. , 1996 Cai and Zhou, Oper. Res. , 1999 Möhring, Schulz and Uetz, J. ACM, 1999 Nino-Mora, Encyclop. Optimiz. , 2001 Cai, Sun and Zhou, Prob. Eng. Inform. Sci. , 2003 Ebben, Hans and Olde Weghuis, OR Spectrum, 2005 Ivanescu, Fransoo and Bertrand, OR Spectrum, 2005 Cai, Wu and Zhou, IEEE Transactions Autom. Sci. Eng. , 2007 Cai, Wu and Zhou, J. Scheduling, 2007; 2011 Cai, Wu and Zhou, Oper. Res. , 2009 Tam, Ehrgott, Ryan and Zakeri, OR Spectrum, 2011 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 14

3. Fuzzy approach Fuzzy scheduling techniques either fuzzify existing scheduling rules or solve mathematical programming problems • Often: fuzzy processing times , fuzzy due dates • Examples • triangular fuzzy processing times PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 trapezoidal fuzzy processing times 15

Often: possibilistic approach (Dubois and Prade 1988) Chanas and Kasperski (2001) Problem Objective: Assumption: → adaption of Lawler‘s algorithm for problem PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 16

Special cases: a) b) c) d) Alternative goal approach - fuzzy goal, Objective: Chanas and Kasperski (2003) Problem Objective: → adaption of Lawler‘s algorithm for problem PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 17

Selected references (1) • • • Dumitru and Luban, Fuzzy Sets and Systems, 1982 Tada, Ishii and Nishida, APORS, 1990 Ishii, Tada and Masuda, Fuzzy Sets and Systems, 1992 Grabot and Geneste, Int. J. Prod. Res. , 1994 Han, Ishii and Fuji, EJOR, 1994 Ishii and Tada, EJOR, 1995 Stanfield, King and Joines, EJOR, 1996 Kuroda and Wang, Int. J. Prod. Econ. , 1996 Özelkan and Duckstein, EJOR, 1999 Sakawa and Kubota, EJOR, 2000 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 18

Selected references (2) • • Chanas and Kasperski, Eng. Appl. Artif. Intell. , 2001 Chanas and Kasperski, EJOR, 2003 Chanas and Kasperski, Fuzzy Sets and Systems, 2004 Itoh and Ishii, Fuzzy Optim. and Dec. Mak. , 2005 Kasperski, Fuzzy Sets and Systems, 2005 Inuiguchi, LNCS, 2007 Petrovic, Fayad, Petrovic, Burke and Kendall, Ann. Oper. Res. , 2008 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 19

4. Robust approach Objective: Find a solution, which minimizes the „worst-case“ performance over all scenarios. Notations (single machine problems) maximal regret of Minmax regret problem (MRP): Find a sequence PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 such that 20

Some polynomially solvable MRP (Kasperski 2005) (Volgenant and Duin 2010) (Averbakh 2006) (Kasperski 2008) Some NP-hard MRP (Lebedev and Averbakh 2006) (for a 2 -approximation algorithm, see Kasperski and Zielinski 2008) (Kasperski, Kurpisz and Zielinski 2012) PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 21

Kasperski and Zielinski (2011) Consideration of MRP‘s using fuzzy intervals Deviation interval Known: deviation Application of possibility theory (Dubois and Prade 1988) possibly optimal if necessarily optimal if PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 22

Fuzzy problem or equivalently where is a fuzzy interval and with membership function is the complement of The fuzzy problem can be efficiently solved if a polynomial algorithm for the corresponding MRP exists. PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 23

Solution approaches a) Binary search method - repeated exact solution of the MRP - applications: : binary search subroutine in B&B algorithm PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 24

b) Mixed integer programming formulation - use of a MIP solver - application: c) Parametric approach - solution of a parametric version of a MRP (often time-consuming) - application: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 25

Selected references (1) • • • Daniels and Kouvelis, Management Sci. , 1995 Kouvelis and Yu, Kluwer, 1997 Kouvelis, Daniels and Vairaktarakis, IEEE Transactions, 2000 Averbakh, OR Letters, 2001 Yang and Yu, J. Comb. Optimiz. , 2002 Kasperski, OR Letters, 2005 Kasperski and Zielinski, Inf. Proc. Letters, 2006 Lebedev and Averbakh, DAM, 2006 Averbakh, EJOR, 2006 Montemanni, JMMA, 2007 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 26

Selected references (2) • • • Kasperski and Zielinski, OR Letters, 2008 Sabuncuoglu and Goren, Int. J. Comp. Integr. Manufact. , 2009 Aissi, Bazgan and Vanderpooten, EJOR, 2009 Volgenant and Duin, COR, 2010 Kasperski and Zielinski, FUZZ-IEEE, 2011 Kasperski, Kurpisz and Zielinski, EJOR, 2012 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 27

5. Stability approach 5. 1. Foundations 5. 2. General shop problem 5. 3. Two-machine flow and job shop problems 5. 4. Problem 28

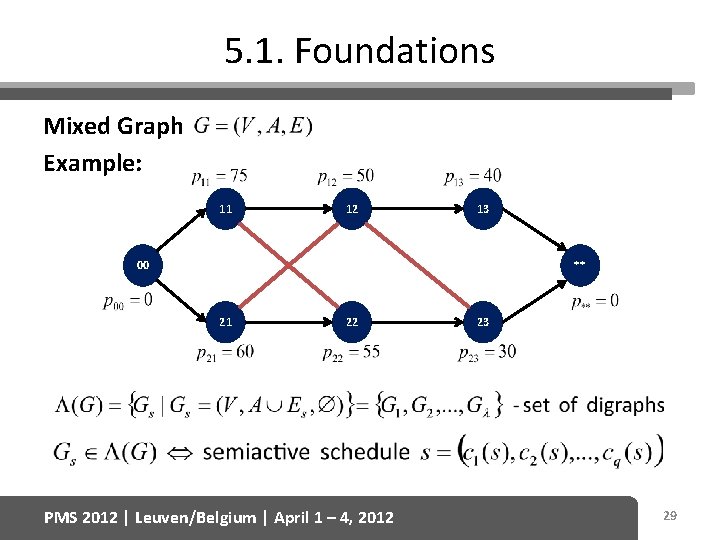
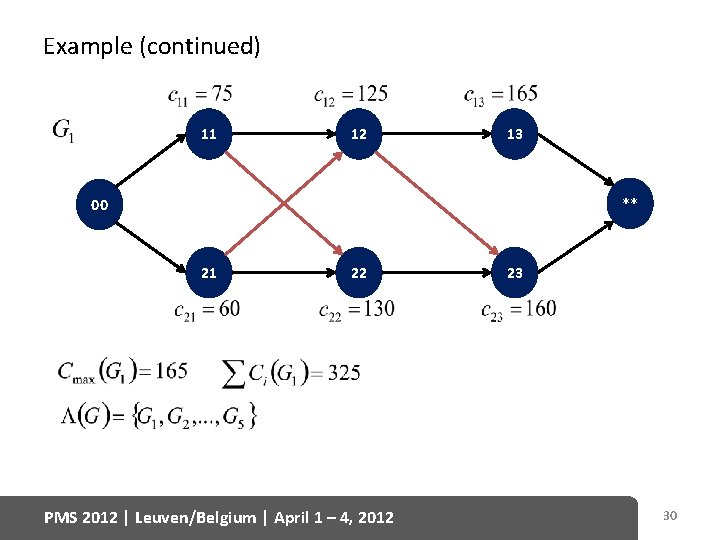
5. 1. Foundations Mixed Graph Example: 11 12 13 00 ** 21 22 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 23 29

Example (continued) 11 12 13 ** 00 21 22 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 23 30

Stability analysis of an optimal digraph Definition 1 The closed ball stability ball of if for any remains optimal. The maximal value is called a is called the stability radius of digraph Known: • Characterization of the extreme values of • Formulas for calculating • Computational results for job shop problems with (see Sotskov, Sotskova and Werner, Omega, 1997) PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 31

5. 2. General shop problem Definition 2 is called a G-solution for problem if for any fixed contains an optimal digraph. If any is not a G-solution, is called a minimal G-solution denoted as Introduction of the relative stability radius: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 32

Definition 3 Let be such that for any The maximal value of of such a stability ball called the relative stability radius is Known: • Dominance relations among paths and sets of paths • Characterization of the extreme values of PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 33

Characterization of a G-solution for problem Definition 4 (strongly) dominates in → dominance relation Theorem 7: is a G-solution. There exists a finite covering of polytope by closed convex sets with such that for any and any there exists a for which Corollary: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 34

Theorem 8: Let be a G-solution with Then: is a minimal G-solution. For any there exists a vector such that Algorithms for problem PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 35

Several 3 -phase schemes: • B&B: implicit (or explicit) enumeration scheme for generating a G-solution • SOL: reduction of different • by generating a sequence with the same and MINSOL: generation of a minimal G-solution a repeated application of algorithm SOL PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 by 36

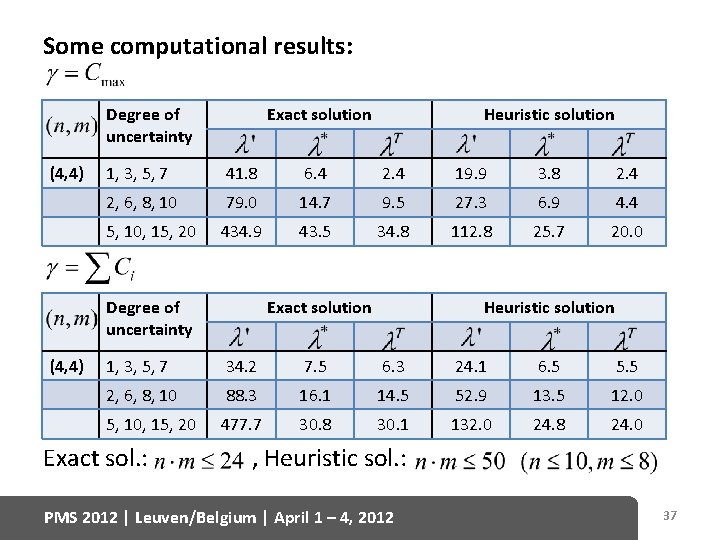
Some computational results: Degree of uncertainty (4, 4) Exact solution 1, 3, 5, 7 41. 8 6. 4 2. 4 19. 9 3. 8 2. 4 2, 6, 8, 10 79. 0 14. 7 9. 5 27. 3 6. 9 4. 4 5, 10, 15, 20 434. 9 43. 5 34. 8 112. 8 25. 7 20. 0 Degree of uncertainty (4, 4) Heuristic solution Exact solution Heuristic solution 1, 3, 5, 7 34. 2 7. 5 6. 3 24. 1 6. 5 5. 5 2, 6, 8, 10 88. 3 16. 1 14. 5 52. 9 13. 5 12. 0 5, 10, 15, 20 477. 7 30. 8 30. 1 132. 0 24. 8 24. 0 Exact sol. : , Heuristic sol. : PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 37

5. 3. Two-machine problems with interval processing times a) Problem Johnson permutation: Partition of the job set PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 38

Theorem 9: (1) for any either (2) ) and if satisfies – – – PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 39

Theorem 10: If then Percentage of instances with , where 5 10 15 20 25 30 1 99. 2 95. 2 91. 2 86. 1 79. 2 72. 8 2 97. 2 89. 8 77. 6 63. 5 51. 0 39. 6 3 95. 0 80. 9 66. 4 47. 6 32. 8 20. 6 4 91. 8 78. 6 56. 0 39. 2 20. 3 10. 7 5 91. 0 69. 4 44. 9 28. 9 14. 6 6. 0 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 40

General case of problem Theorem 11: There exists an Theorem 12: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 41

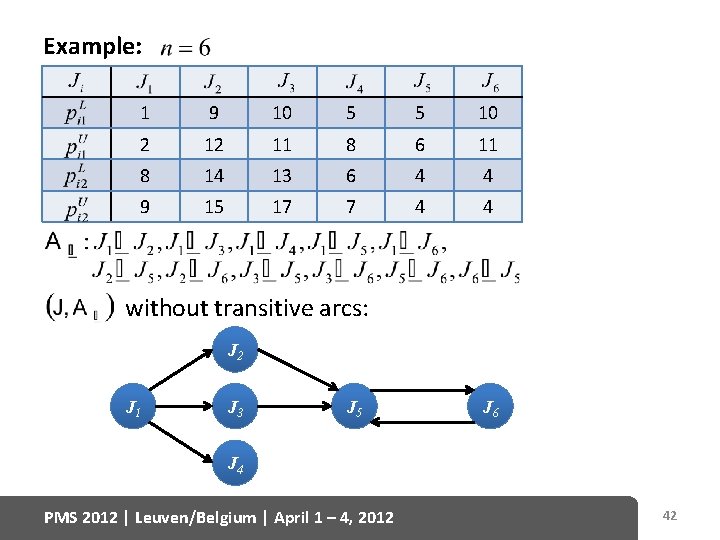
Example: 1 9 10 5 5 10 2 12 11 8 6 11 8 14 13 6 4 4 9 15 17 7 4 4 without transitive arcs: J 2 J 1 J 3 J 5 J 6 J 4 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 42

Properties of in the case of see Matsveichuk, Sotskov and Werner, Optimization, 2011 Schedule execution phase: see Sotskov, Sotskova, Lai and Werner, Scheduling under uncertainty, 2010 (Section 3. 5) Computational results for and for b) Problem → Reduction to two problems: see Sotskov, Sotskova, Lai and Werner, Scheduling under uncertainty, 2010 (Section 3. 6) PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 43

5. 4. Problem Notations: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 44

Definition of the stability box: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 45

Definition 5 The maximal closed rectangular box is a stability box of permutation , if permutation being optimal for instance with a scenario remains optimal for the instance with a scenario for each If there does not exist a scenario such that permutation is optimal for instance , then Remark: The stability box is a subset of the stability region. However, the stability box is used since it can easily be computed. PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 46

Theorem 13: For the problem , job if and only if the following inequality holds: Lower (upper) bound on the range of optimality of : PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 dominates preserving the 47

Theorem 14: If there is no job , in permutation such that inequality holds for at least one job , then the stability box is calculated as follows: otherwise PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 48

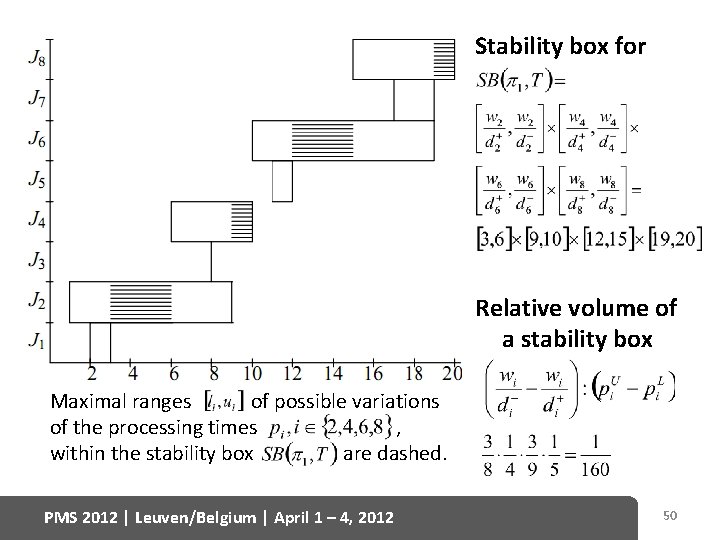
Example: Data for calculating PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 49

Stability box for Relative volume of a stability box Maximal ranges of possible variations of the processing times , within the stability box are dashed. PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 50

Sotskov, Egorova, Lai and Werner (2011) Derivation of properties of a stability box that allow to derive an algorithm MAX-STABOX for finding a permutation with • the largest dimension and • the largest volume of a stability box PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 51

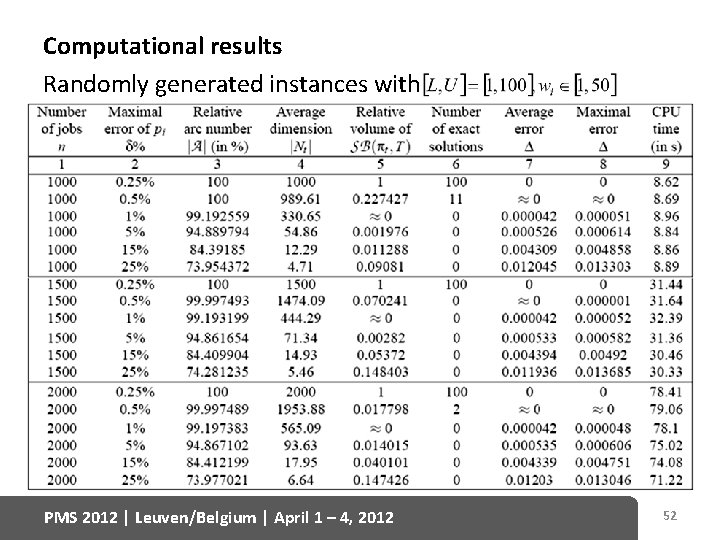
Computational results Randomly generated instances with PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 52

Selected references • • Lai, Sotskova and Werner, Math. Comp. Model. , vol. 26, 1997 Sotskov, Wagelmans and Werner, Ann. Oper. Res. , vol. 38, 1998 Lai, Sotskova and Werner, Eur. J. Oper. Res. , vol. 159, 2004 Sotskov, Egorova and Lai, Math. Comp. Model. , vol. 50, 2009 Sotskov, Egorova and Werner, Aut. Rem. Control, vol. 71, 2010 Sotskov, Egorova, Lai and Werner, Proceedings SIMULTECH, 2011 Sotskov and Lai, Comp. Oper. Res. , vol. 39, 2012 Sotskov, Lai and Werner, Manuscript, 2012 PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 53

6. Selection of a suitable approach Problem Cardinality of Theorem 15: PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 54

Theorem 16: Assume that there is no Then: Theorem 17: not uniquely determined Construct an equivalent instance with less jobs for which is uniquely determined Assumption: uniquely determined. - instance with the set of scenarios PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 55

Uncertainty measures Dominance graph Recommendations: use a stability approach use a robust approach use a fuzzy or stochastic approach PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 56

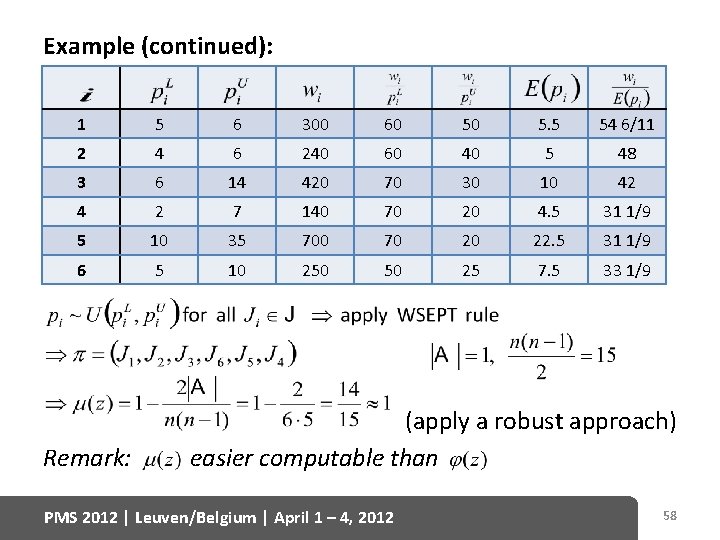
Example: 1 5 6 300 60 50 2 4 6 240 60 40 3 6 14 420 70 30 4 2 7 140 70 20 5 10 35 700 70 20 6 5 10 250 50 25 Dominance conditions: apply a stochastic or a fuzzy approach PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 57

Example (continued): 1 5 6 300 60 50 5. 5 54 6/11 2 4 6 240 60 40 5 48 3 6 14 420 70 30 10 42 4 2 7 140 70 20 4. 5 31 1/9 5 10 35 700 70 20 22. 5 31 1/9 6 5 10 250 50 25 7. 5 33 1/9 Remark: (apply a robust approach) easier computable than PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 58

Announcement of a book Sequencing and Scheduling with Inaccurate Data Editors: To appear at: Completion: Yuri N. Sotskov and Frank Werner Nova Science Publishers Summer 2013 4 parts: Each part contains a survey and 2 -4 further chapters. Part 1: Part 2: Part 3: Part 4: Stochastic approach Fuzzy approach Robust approach Stability approach Contact address: survey: Cai et al. survey: Sakawa et al. survey: Kasperski and Zielinski survey: Sotskov and Werner frank. werner@ovgu. de PMS 2012 | Leuven/Belgium | April 1 – 4, 2012 59