Razonamiento Cuantitativo GEMA 1000 Dr Edwin Alfonso Unidad

Razonamiento Cuantitativo GEMA 1000 Dr. Edwin Alfonso Unidad 1

Primera Unidad: Números Reales Capitulo 6 n Subconjuntos de los números Reales n Propiedades de los números Reales n Orden de operaciones y valor absoluto de un numero real. n Aplicaciones

Capacitantes n Reconocer los subconjuntos del sistema de los números reales. n Clasificar un numero dentro del sistema de números reales. n Efectuar las operaciones de adición, sustracción, multiplicación y división en los números reales. n Determinar valor absoluto, potencia y raíz enésima de un numero real.

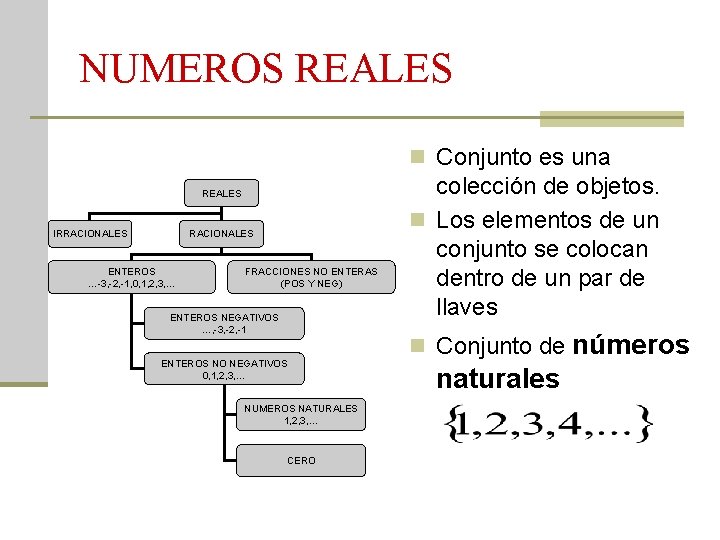
NUMEROS REALES n Conjunto es una REALES IRRACIONALES ENTEROS …-3, -2, -1, 0, 1, 2, 3, … FRACCIONES NO ENTERAS (POS Y NEG) ENTEROS NEGATIVOS …, -3, -2, -1 ENTEROS NO NEGATIVOS 0, 1, 2, 3, … NUMEROS NATURALES 1, 2, 3, … CERO colección de objetos. n Los elementos de un conjunto se colocan dentro de un par de llaves n Conjunto de naturales números

Conjunto: Enteros no negativos (números cardinales) n Los enteros positivos y el cero conforman el conjunto de los números enteros no negativos. n El cero no tiene signo: no es positivo y no es negativo. Números enteros no negativos 0 1 2 3

Conjunto: Enteros negativos n Los enteros negativos son necesarios para describir situaciones como: Temperatura bajo cero: -10˚ n Déficit en una cuenta de banco: -$40 n Física: dirección de una fuerza F = -10 N n n -1 es mayor que el -3

Conjunto Enteros Recta numérica (recta de los números reales) muestra a el conjunto de los enteros origen Números enteros negativos -3 -2 -1 Números enteros no negativos 0 1 2 3

Conjunto: Números Racionales n {Enteros} → {Enteros negativos; enteros no negativos} n Para las siguientes situaciones tenemos que incluir fracciones Trabajo: 8 ½ horas n Me perdí la mitad (1/2) de la película n Costo de un articulo: $1. 25 = $ 1 ¼ n n {Racionales} → {Enteros; fracciones no enteras}

Posición de los números racionales Recta numérica (recta de los números reales) ejemplo de números racionales. origen 1/2 -3 -2 -1 0 1 2 3

Def. Numero Racional n A un numero real se le llama racional si puede escribirse como el cociente p / q de dos enteros, donde q ≠ 0 (q distinto de cero). n Ejemplos

Def. Numero Irracional n Los números reales que no pueden escribirse como cocientes de dos enteros se denominan irracionales. n Ejemplos n La representación de un numero irracional no termina ni se repite. n Ejemplos: solo se aproxima

Ejercicio: n Determine los números naturales, enteros, racionales e irracionales del siguiente conjunto.

Ejercicio: n Determine los números naturales, enteros, racionales e irracionales del siguiente conjunto.

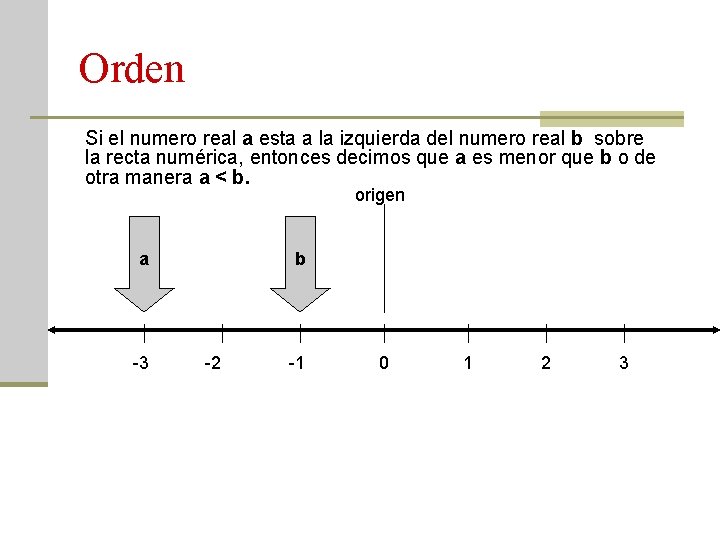
Orden Si el numero real a esta a la izquierda del numero real b sobre la recta numérica, entonces decimos que a es menor que b o de otra manera a < b. origen a -3 b -2 -1 0 1 2 3

Distancia Si a o b son dos números reales tales que a ≤ b, entonces la distancia entre a y b es: (distancia entre a y b)= b - a a -3 origen b -2 -1 0 Ex: Determine la distancia entre -3 y -1 Distancia entre -3 y -1 = -1 -(-3)=-1+3=2 determine la distancia entre 0 y 3 Distancia entre 0 y 3 = 3 - 0= 3 1 2 3

Ejercicios n Ej. 5: Dibuje el siguiente conjunto en una recta numérica. n {-1/2, 3/4, 5/3, 7/2} origen -1/2 -3 -2 -1 3/4 0 1 5/3 2 7/2 3 4

Tarea n Pág. 261 n Ejercicios sección 6. 1 n 1, 3, 5, 7, 9, 13, 15, 17, 19, 27, 45, 47, 49, 51, 61 -68

Ejercicios n Diga si es verdadero o falso Cierto. -2 esta a la izquierda de -1 n -2 < -1 Falso. -15 esta a la derecha de -20 n -15 ≤ -20 Cierto. -8 ≤ 4 n -8 ≤ -(-4); Cierto 6 > 2 n 6 > -(-2) F n Todo numero racional es un entero. n Todo numero entero es un numero racional. C n Algunos números racionales son irracionales. C n Algunos números racionales son enteros. F

Valor absoluto n A la distancia entre un numero real a y 0 (el origen) se le llama valor absoluto de a. Un par de barras verticales sirven para indicar el valor absoluto. Ex: |a| n El valor absoluto de un numero real a se define como la distancia entre a y 0 sobre la recta numérica. n Regla Si a ≥ 0 entonces |a|=a. ex: |3|=3 n Si a ≤ 0 entonces |a|=-a. ex: |-2|= -(-2)=2 n

Simplifique: Ejercicios 61, 63, 65, 67 Pág. 262 n |3|= 3 n -|7|= -7 n |7 -4|= 3 n -|-(5 -1)|= - | -4 |= -4

Propiedades de la adición: signos iguales n Suma de números reales n n Primer caso: signos iguales. Para sumar dos números con el mismo signo, deben sumarse sus valores absolutos. El signo de la suma (+ o -) es el mismo que el signo de los dos números. Ej. Para sumar -12 y -8, necesitamos sus valores absolutos n |-12|=12 ; |-8|=8 n Como ambos tienen signo negativo, usamos la regla anterior. Por lo tanto sumamos los valores absolutos: 12+8=20. Luego dé a la suma el signo de los dos números. Como ambos números son negativos la suma es negativa. n -12 + (-8) = -20

Propiedades de la adición: signos diferentes n Suma de números reales n n segundo caso: signos diferentes. Para sumar dos números con signo diferente debe restarse el valor absoluto mas pequeño del mas grande. La suma es positiva si el numero positivo tiene el valor absoluto mas grande. La suma es negativa si el numero negativo posee el valor absoluto mas grande. Ej. Para sumar -17 +11, necesitamos sus valores absolutos n |-17|=17 ; |11|=11 n Restando 17 -11=6 n De al resultado el signo del numero con mayor valor absoluto. Por lo tanto, será -6. n Conclusión: -17+11= -6

Ejemplos n (-6)+(-3)= - (6+3)=-9 n (-12)+(-4)= -(12+4)=-16 n 4+(-1)=3 n -9+16=7 n -16+12=-4

Sustracción o diferencia de números reales n Definición. n Para todos los números reales a y b, a - b = a + (-b) O sea cambie el signo del segundo numero y sume. 6 – 8 = 6 + (-8) = -2 Cambie a suma y cambia el signo del segundo numero. Cambie a suma y busque el inverso aditivo.

Ejemplos n -12 – 4 = -12 + (- 4) = -16 Cambia a suma Signo cambiado (inverso aditivo) -10 – (-7) = -10 + 7= - 3 Cuando se resuelve un problema con sumas y restas, las sumas y las restas se realizan en orden de izquierda a derecha. 15 – (-3) – 5 – 12 = 15 + 3 + (-5) + (-12) = = (15 + 3) + (-5) + (-12) = 18 + (-5) + (-12) = = (18 + (-5) ) + (-12) = = 13 + (-12) = 1

Multiplicación de números reales n Razonamiento Inductivo 4 • 5 = 20 4 • 4 = 16 4 • 3 = 12 4 • 2=8 4 • 1=4 4 • 0=0 = -4 4 • (-1) = ?

Multiplicación de números reales n Razonamiento Inductivo 4 • (-1) = -4 4 • (-2) = -8 4 • (-3) = -12 4 • (-4) = -16 n De la misma manera -4 • 2 = -8 -4 • 3 = -12 -4 • 4 = -16

Multiplicación de números reales n Caso 1: signos iguales. Para multiplicar dos números con el mismo signo, multiplique sus valores absolutos. El producto es positivo. n Caso 2 : signos diferentes. Para multiplicar dos números con signos diferentes, multiplique sus valores absolutos. El producto es negativo. n Ejemplos n n n - 9 • 7= -63 -14 • (-5) = 70 -8 • (-4) = 32

División de números reales n El resultado que se consigue al dividir dos números reales se conoce con el nombre de cociente. Para números reales a, b y c, donde b ≠ 0, a/b= c significa que a=b • c. Para ilustrar esto, considere.

División de números reales n Signos iguales. Para dividir dos números con el mismo signo, deben dividirse sus valores absolutos. El cociente es positivo. n Signos diferentes. Para dividir dos números con signos diferentes, hay que dividir sus valores absolutos. El cociente es negativo.

DI VI S IO N EN TR E 0 N O ES T numero diferente de cero, el cociente es 0. n Siempre que se realiza una división, queremos obtener un solo cociente. n ¿Que numero multiplicado por cero resulta en 7? n ¿Que numero multiplicado por cero resulta en 0? A n Si 0 se divide entre un DE FIN ID A División con cero NINGUNO NUMERO INFINITO DE RESPUESTAS

Exponentes enteros positivos n un entero positivo y a un numero real. Entonces el producto de n factores de a esta n Sea dado por Exponente an= a • a … • a. BASE

Ejemplo: Calculo de expresiones exponenciales n Cuidado (-a )n ≠ -an n (-3)4=(-3)(-3) = 81 n -34= - (3)(3) = - 81 n - (-3)4= - (-3)(-3) = - 81

Orden de las operaciones n Si hay paréntesis o corchetes: n Paso 1: Resuelva arriba y debajo de las rayas de fracciones por separado. n Paso 2: Utilice las reglas siguientes dentro de cada conjunto de paréntesis o corchetes. Inicie con el conjunto mas interno y trabaje hacia fuera. n Si no hay paréntesis o corchetes n Paso 1: aplique todos los exponentes n Paso 2: Haga las multiplicaciones o divisiones en el orden en que aparezcan, trabajando de izquierda a derecha. n Paso 3: Haga las sumas y restas en el orden en que aparezcan, trabajando de izquierda a derecha.

Tarea n Ejercicios. Pag 271 n 7, 9, 11, 13, 15, 17, 19, 21, 25, 29, 31, 33, 35, 39

Propiedades de la suma y la multiplicación de números reales n Para los números reales, a, b y c, se cumplen las siguientes propiedades. n Propiedades de cierre n Si a y b son números reales, entonces a + b y ab son números reales.

Propiedades de la suma y la multiplicación de números reales n. Propiedades conmutativas a+b=b+a n. Ej. ab = ba 4 + (3 + 9) = 4 + (9 + 3) 4 + 12 = 4 + 12 16 = 16 4(5)=5(4)=20

Propiedades de la suma y la multiplicación de números reales n. Propiedades asociativas (a + b) + c = a + (b + c) (ab)c = a(bc) Ej. 5 + (6 + 8) = (5 + 6) + 8 (5 • 2)3 = 5(2 • 3)=30

Propiedades de la suma y la multiplicación de números reales n. Propiedades distributiva de la multiplicación con respecto a la suma a(b+c) = ab + ac (b+c)a = ba + ca n. Ej. n 5(x + y) = 5 x + 5 y

Propiedades de la suma y la multiplicación de números reales n Propiedades de la identidad n Existe un numero real 0 tal que na + 0 = a y 0 + a = a n Existe un numero real 1, tal que n a • 1= a y 1 • a = a n Ej. 8+0=8

Propiedades de la suma y la multiplicación de números reales n Propiedad del inverso aditivo: La suma de un numero real y su opuesto es cero. a + (-a) =0 n Ej. 5 + (-5) =0 n n Propiedad del inverso multiplicativo: El producto de un numero real diferente de cero y su reciproco es 1. n a • 1/a = 1, a ≠ 0

Ejercicios n Identifique la propiedad ilustrada en cada una de las siguientes proposiciones. n 6 + 9 = 9 + 6 Conmutativa de la suma n 7 + (2 + 5) = (7 + 2 ) + 5 n 9 • 6 + 9 • 8 = 9 (6 + 8) Asociativa de la suma distributiva

Ejercicio b + 2 = 6 Ecuación dada (b + 2) + (-2) = 6 + (-2) Propiedad aditiva de Igualdad b + [2 + (-2)] =4 Propiedad asociativa de la suma b + 0 = 4 Propiedad del inverso aditivo b=4 Propiedad de identidad aditiva

Tarea n Ejercicios, Pág. 271 n 41, 43, 45, 47, 49, 52

Aplicaciones n El record de temperatura mas alta , de 134˚F, en Estados Unidos fue registrado en el Valle de la Muerte, California, en 1913. El record de temperatura mas baja fue de – 80 ˚F en Prospect Creek, Alaska, en 1971. ¿Cual es la diferencia entre la temperatura mas alta y la mas baja? n 134 – (-80) = 134 + 80 = 214 n La diferencia es 214 ˚F

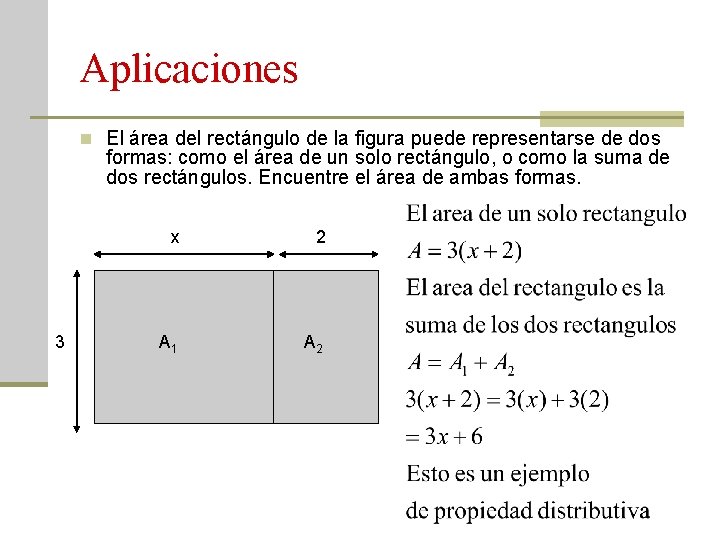
Aplicaciones n El área del rectángulo de la figura puede representarse de dos formas: como el área de un solo rectángulo, o como la suma de dos rectángulos. Encuentre el área de ambas formas. 3 x 2 A 1 A 2

Aplicaciones Ejercicio 73 Pág. 273 En 1990, los ingresos netos de instituciones de ahorro (en millones de dólares) para los estados del noroeste de los Estados Unidos fueron los siguientes. n ¿Cual fue el total de los ingresos netos? n n Estado Ingresos netos (millones de dólares) Maine 0 New Hampshire -24 Vermont 2 Massachusett s -212 Rhode Island -13 Connecticut -149

Tarea n Pág. 273 -274 Sección 6. 2 n Ejercicio 76, 85, 87.