Quantum Unertainty Relations and Some Applications Archan S

Quantum Unertainty Relations and Some Applications Archan S. Majumdar S. N. Bose National Centre for Basic Sciences, Kolkata

Plan: • Various forms of uncertainty relations: Heisenberg Robertson-Schrodinger Entropic Fine-grained …… Error-disturbance …………… • Applications: Purity & mixedness EPR paradox and steering Nonlocality (bipartite, tripartite & biased games) Quantum memory (Information theoretic task: quantum memory as a tool for reducing uncertainty) Key generation (lower limit of key extraction rate)

Uncertainty Principle: Uncertainty in observable A: Consider two self-adjoint operators Now, Minimizing l. h. s w. r. t , thus Hence, one gets or For canonically conjugate pairs of observables, e. g. , (Heisenberg Uncertainty Relation)

Heisenberg uncertainty relation: Scope for improvement: State dependence of r. h. s. ? higher order correlations not captured by variance ? Effects for mixed states ? Various tighter relations, e. g. , Robertson-Schrodinger:

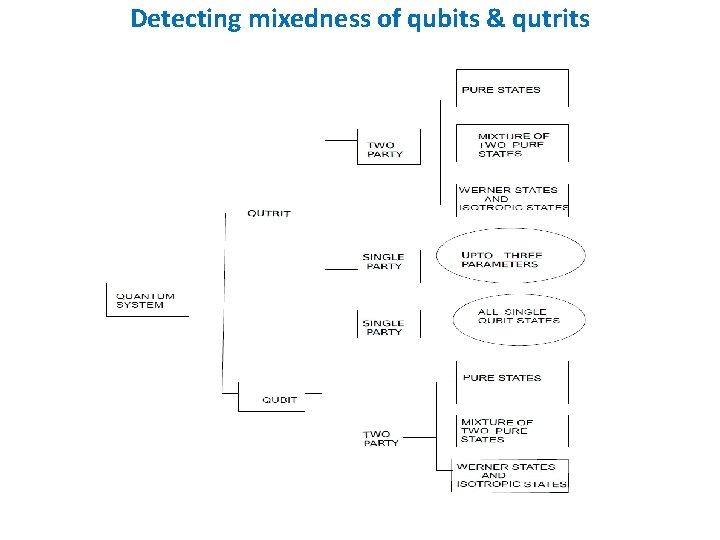
Application of RS uncertainty relation: detecting purity and mixedness S. Mal, T. Pramanik, A. S. Majumdar, Phys. Rev. A 87, 012105 (2013) Problem: Set of all pure states not convex. Approach: Consider generalized Robertson-Schrodinger uncertainty relation Choose operators A and B such that For pure states: For mixed states: [Linear Entropy]

Qubits: Choose, . , Generalized uncertainty as measure of mixedness (linear entropy) For pure states: For mixed states: gives Results extendable to n-qubits and single and bipartite qutrits

Examples: 2 -qubits: (Observables) Linear entropy: Qutrits: Isotropic states: Observables: Linear entropy:

Detecting mixedness of qubits & qutrits

Entropic uncertainty relations:

Application of HUR & EUR Demonstration of EPR Paradox & Steering

EPR Paradox [Einstein, Podolsky, Rosen, PRA 47, 777 (1935)] Assumptions: (i) Spatial separability & locality: no action at a distance (ii) reality: “if without in any way disturbing the system, we can predict with certainty the value of a physical quantity, then there exists an element of physical reality corresponding to this quantity. ” EPR considered two spatially separated particles with maximum correlations in their positions and momenta Measurement of position of 1 implies with certainty the position of 2 (definite predetermined value of position of 2 without disturbing it) Similarly, measurement of momentum of 1 implies momentum of 2 (again, definite predetermined value of momentum of 2 without disturbing it) Hence, particle 2 in a state of definite position and momentum. Since no state in QM has this property, EPR conclude that QM gives an incomplete description of the state of a particle.

EPR Paradox & Steering Einstein’s later focus on separability and locality versus completeness Consider nonfactorizable state of two systems: If Alice measures in she instantaneously projects Bob’s system into one of the states and similarly, for the other basis. Since the two systems no longer interact, no real change can take place in Bob’s system due to Alice’s measurement. However, the ensemble of is different from the ensemble of EPR: nonlocality is an artefact of the incompleteness of QM. Schrodinger: Steering: Alice’s ability to affect Bob’s state through her choice of measurement basis.

Steering: [Schrodinger, Proc. Camb. Phil. Soc. 31, 555 (1935) Alice can steer Bob’s state into either upon her choice of measurement or depending “It is rather discomforting that theory should allow a system to be steered …… into one or the other type of state at the experimenter’s mercy in spite of having no access to it. ” (Shrodinger: Steering not possible experimentally, hence QM not correct for delocalized (entangled) systems)

EPR Paradox: a testable formulation [M. Reid, Phys. Rev. A 40, 913 (1989)] [Application of Uncertainty Relation] Analogous to position and momentum, consider quadratures of two correlated and spatially separated light fields. Correlations : (with some error) Estimated amplitudes:

EPR paradox (Reid formulation…. ) [Tara & Agarwal, PRA (1994)] Average errors of inferences: chosen for highest possible accuracy Uncertainty principle: > 1 EPR paradox occurs if above inequality is violated due to correlations. (c. f. , experimental violation with light modes, Ou et al. PRL (1992))

Steering: a modern perspective [Wiseman et al. , PRL (2007)] Steering as an information theoretic task. Leads to a mathematical formulation Steering inequalities, in the manner of Bell inequalities

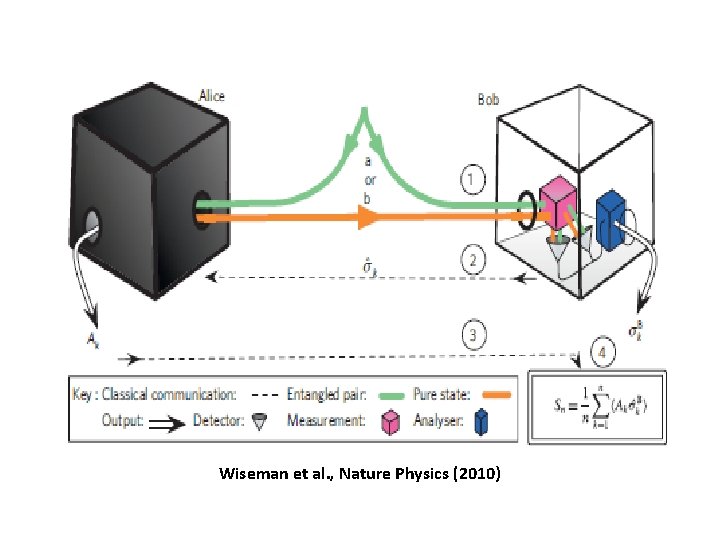
Steering as a task [Wiseman, Jones, Doherty, PRL 98, 140402 (2007); PRA (2007)] (Asymmetric task) Local Hidden State (LHS): Bob’s system has a definite state, even if it is unknown to him Experimental demonstration: Using mixed entangled states [Saunders et al. Nature Phys. 6, 845 (2010)]

Steering task: (inherently asymmetric) Alice prepares a bipartite quantum state and sends one part to Bob (Repeated as many times) Alice and Bob measure their respective parts and communicate classically Alice’s taks: To convince Bob that the state is entangled (If correlations between Bob’s measurement results and Alice’s declared results can be explained by LHS model for Bob, he is not convinced. – Alice could have drawn a pure state at random from some ensemble and sent it to Bob, and then chosen her result based on her knowledge of this LHS). Conversely, if the correlations cannot be so explained, then the state must be entangled. Alice will be successful in her task of steering if she can create genuinely different ensembles for Bob by steering Bob’s state.

Wiseman et al. , Nature Physics (2010)

Steering inequalities: [Motivations] Demonstration of EPR paradox (Reid inequalities) based on correlations up to second order Several CV states do not violate Reid inequality Correlations may be hidden in higher order moments of observables Similarly, Heisenberg uncertainty relation based on variances Extension to higher orders: Entropic uncertainty relation

Entropic steering inequality [Walborn et al. , PRL (2011)] Condition for non-steerability: (1) Now, the conditional probability (2) (follows from (1) – LHS for Bob, and rule for conditional probabilities: Hence, for (3) [(2), (3) are non-steering conditions equivalent to (1)]

Entropic steering inequality [Walborn et al. , PRL (2011)] (some definitions): Relative entropy: H(p(X)||q(X)) = Conditional entropy: H(X|Y) = Now, using: H(X|Y) = (can be negative for entangled states) H(X|Y) = H(XY) - H(Y) Shannon Entropy (or, von-Neuman, for quantum case)

Entropic inequality Consider relative entropy between the probability distributions: Positivity of relative entropy: (variables are and given )

Entropic steering inequality Use non-steering condition (2): It follows that: Hence,

Entropic steering inequality … Averaging over all Now, consider conjugate variable pairs: Similarly, Hence, (5)

Entropic steering relations Entropic uncertainty relation for conjugate variables R and S: (Bialynicki-Birula & Mycielski, Commun. Math. Phys. (1975)) (6) LHS model for Bob: [(6) holds for each state marked by ]: Averaged over all hidden variables: Hence, using (5), ESR:

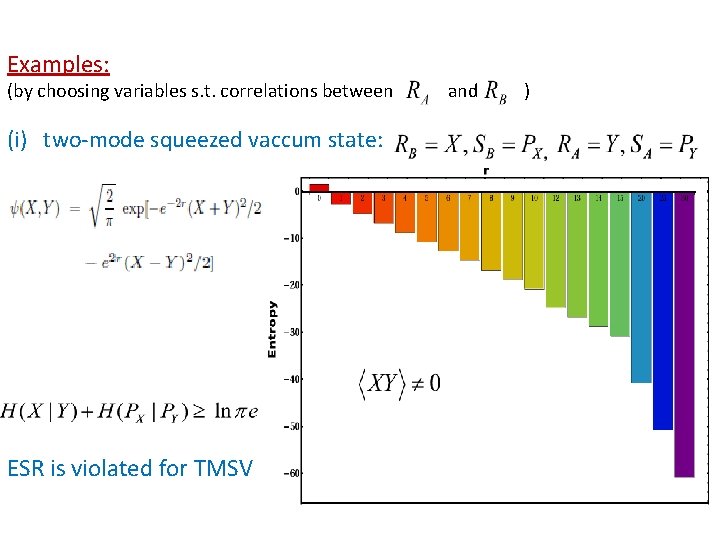
Examples: (by choosing variables s. t. correlations between (i) two-mode squeezed vaccum state: ESR is violated for TMSV and )

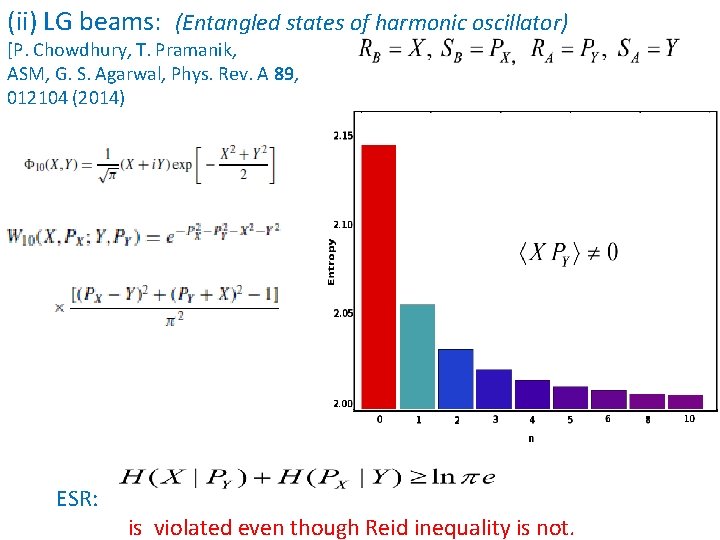
(ii) LG beams: (Entangled states of harmonic oscillator) [P. Chowdhury, T. Pramanik, ASM, G. S. Agarwal, Phys. Rev. A 89, 012104 (2014) ESR: is violated even though Reid inequality is not.

Uncertainty Relations Heisenberg uncertainty relation (HUR) : For any two non-commuting observables, the bounds on the uncertainty of the precision of measurement outcome is given by Robertson-Schrodinger uncertainty relation: For any two arbitrary observables, the bounds on the uncertainty of the precision of measurement outcome is given by Applications : ➢ Entanglement detection. ➢ Witness for mixedness. (PRA 78, 052317 (2008). ) (PRA 87, 012105 (2013). ) Drawbacks : (1) The lower bound is state dependent. (2) Captures correlations only up to 2 nd order (variances)

Entropic uncertainty relation (EUR) : Where denotes the Shannon entropy of the probability distribution of the measurement outcomes of the observable Applications : ➢ Used to detect steering. [PRL 106, 130402 (2011); PRA 89 (2014). ] ➢ Reduction of uncertainty using quantum memory [Nature Phys. 2010] Drawback : ➢ Unable to capture the non-local strength of quantum physics.

Coarse-grained uncertainty relation In both HUR and EUR we calculate the average uncertainty where average is taken over all measurement outcomes Fine-grained uncertainty relation ➢ In fine-grained uncertainty relation, the uncertainty of a particular measurement outcome or any combination of outcomes is considered. ➢Uncertainty for the measurement of i-th outcome is given by Advantage ➢ FUR is able to discriminate different no-signaling theories on the basis of the non-local strength permitted by the respective theory. J. Oppenheim and S. Wehner, Science 330, 1072 (2010)

Fine-grained uncertainty relation [Oppenheim and Weiner, Science 330, 1072 (2010)] (Entropic uncertainty relations provide a coarse way of measuring uncertainty: they do not distinguish the uncertainty inherent in obtaining any combination of outcomes for different measurements) Measure of uncertainty: If or , then the measurement is certain corresponds to uncertainty in the measurement FUR game: Alice & Bob receive binary questions and (projective spin measurements along two different directions at each side), with answers `a’ and `b’. Winning Probability: : set of measurement settings : measurement of observable A is some function determining the winning condition of the game

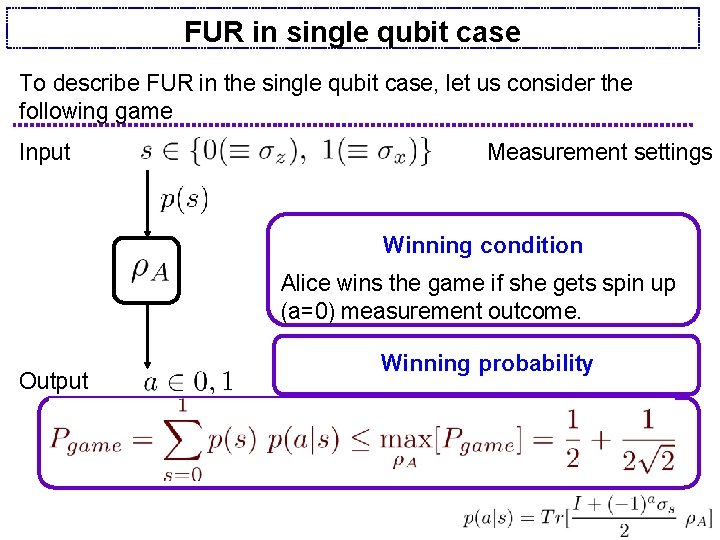
FUR in single qubit case To describe FUR in the single qubit case, let us consider the following game Input Measurement settings Winning condition Alice wins the game if she gets spin up (a=0) measurement outcome. Output Winning probability

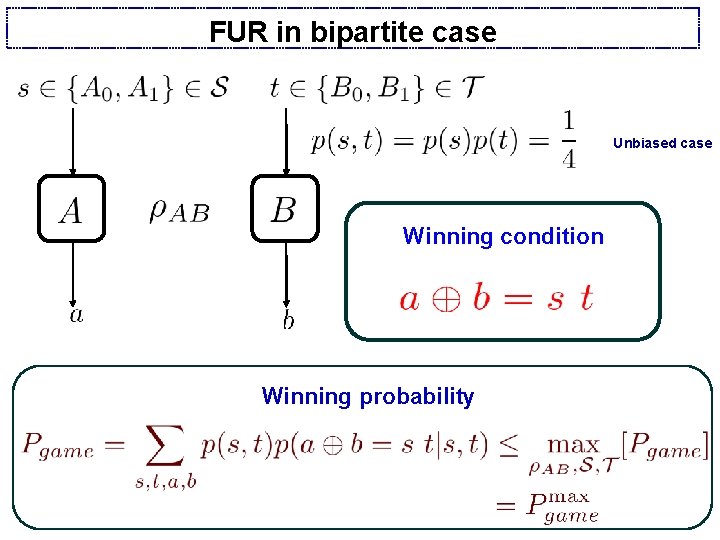
FUR in bipartite case Unbiased case Winning condition Winning probability

FUR for two-qubit CHSH game Connecting uncertainty with nonlocality Classification of physical theory with respect to maximum winning probability

Application of fine-grained uncertainty relation Fine-grained uncertainty relation and nonlocality of tripartite systems: [T. Pramanik & ASM, Phys. Rev. A 85, 024103 (2012)] FUR determines nonlocality of tripartite systems as manifested by the Svetlichny inequality, discriminating between classical physics, quantum physics and superquantum (nosignalling) correlations. [Tripartite case: ambiguity in defining correlations; e. g. , Mermin, Svetlichny types]

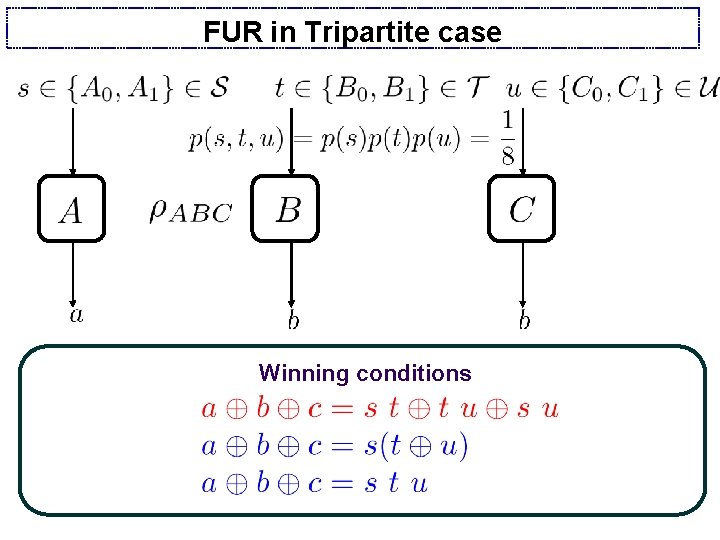
FUR in Tripartite case Winning conditions

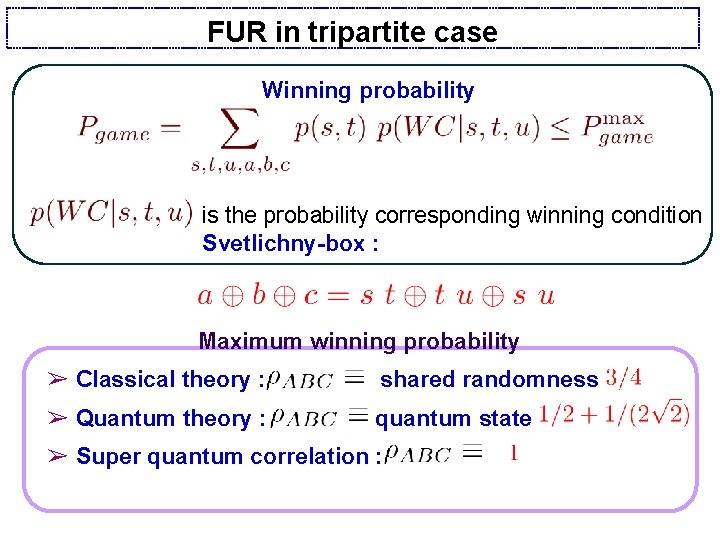
FUR in tripartite case Winning probability is the probability corresponding winning condition Svetlichny-box : Maximum winning probability ➢ Classical theory : shared randomness : ➢ Quantum theory : quantum state : ➢ Super quantum correlation :

Nonlocality in biased games For both bipartite and tripartite cases the different nosignaling theories are discriminated when the players receive the questions without bias. Now the question is that if each player receives questions with some bias then what will be the winning probability for different no-signaling theories

Fine-grained uncertainty relations and biased nonlocal games: [A. Dey, T. Pramanik & ASM, Phys. Rev. A 87, 012120 (2013)] FUR discriminates between the degree of nonlocal correlations in classical, quantum and superquantum theories for a range [not all] of biasing parameters.

FUR in biased bipartite case Consider the case where Maximum winning probability ➢ Classical theory : ➢ Quantum theory : i. For ii. For ➢ Super quantum correlation : Note that the result for the case where , , is same as above

FUR in Biased Tripartite case Winning condition To get the winning probability, we consider a trick called bi-partition model where Alice and Bob play a bipartite game with probability r and another unitarily equivalent game with probability (1 -r). At the end they calculate the average winning probability where average is taken over probability r. PRL 106, 020405 (2011). A. Dey, T. Pramanik, and A. S. Majumdar, PRA 87, 012120 (2013)

FUR in Biased Tripartite case Consider the case where Maximum average winning probability of the game ➢ Classical theory : ➢ Quantum theory : i. For , ii. For ➢ Super quantum correlation : Note that the result for the case where , is same as above A. Dey, T. Pramanik, and A. S. Majumdar, PRA 87, 012120 (2013)

Uncertainty in the presence of correlations [Berta et al. , Nature Physics 6, 659 (2010)]

Reduction of uncertainty: a memory game [Berta et al. , Nature Physics 6, 659 (2010)] Bob prepares a bipartite state and sends one particle to Alice performs a measurement and communicates to Bob her choice of the observable P or Q, but not the outcome By performing a measurement on his particle (memory) Bob’s task is to reduce his uncertainty about Alice’s measurement outcome The amount of entanglement reduces Bob’s uncertainty Example: Shared singlet state: Alice measures spin along, e. g. , x- or z- direction. Bob perfectly successful; no uncertainty.

Experimental reduction of uncertainty

Tighter lower bound of uncertainty: [Pati et al. , Phys. Rev. A 86, 042105 (2012)] Role of more general quantum correlations, viz. , discord in memory Discord: Mutual information: Classical information:

Optimal lower bound of entropic uncertainty using FUR [T. Pramanik, P. Chowdhury, ASM, Phys. Rev. Lett. 110, 020402 (2013)] Derivation: Consider EUR for two observables P and Q: Fix FUR: (without loss of generality) and minimize entropy w. r. t Q

Examples: [TP, PC, ASM, PRL 110, 020402 (2013)] Singlet state: (Uncertainty reduces to zero) Werner state: Fine-grained lower limit: Lower limit using EUR (Berta et al. ):

Examples: ……. [TP, PC, ASM, PRL 110, 020402 (2013)] State with maximally mixed marginals: Fine-grained lower bound: EUR lower bound (Berta et al. ): Optimal lower limit achieveble in any real experiment not attained in practice

Application: Security of key distribution protocols: Uncertainty principle bounds secret key extraction per state Rate of key extraction per state: [Ekert, PRL (1991); Devetak & Winter, PROLA (2005); Renes & Boileau, PRL (2009); Berta et al. , Nat. Phys. (2010)] Rate of key extraction using fine-graining: [TP, PC, ASM, PRL (2013)] FUR: Optimal lower bound on rate of key extraction:

Explanation of optimal lower limit in terms of physical resources: [T. Pramanik, S. Mal, ASM, ar. Xiv: 1304. 4506] In any operational situation, fine-graining provides the bound to which uncertainty may be reduced maximally. Q: What are the physical resources that are responsible for this bound ? ------ not just entanglement ---- Is it discord ? [c. f. , Pati et al. ] : However, FUR optimal lower bound is not always same, e. g. , for A: Requires derivation of a new uncertainty relation

The memory game: Bob prepares a bipartite state and sends one particle to Alice performs a measurement on one of two observables R and S, and communicates her choice [not the outcome] to Bob’s task is to infer the outcome of Alice’s measurement by performing some operation on his particle (memory). Q: What information can Bob extract about Alice’s measurement outcome ? Classical information contains information about Alice’s outcome when she measures alsong a particular direction that maximizes In the absence of correlations, Bob’s uncertainty about Alice’s outcome is When Bob measure the observable R, the reduced uncertainty is where

Derivation of a new uncertainty relation (memory game): [TP, SM, ASM, ar. Xiv: 1304. 4506] When Alice and Bob measure the same observable R, the reduced uncertainty given by the conditional entropy becomes Extractable classical information: Similarly, for S: Apply to EUR: New uncertainty relation:

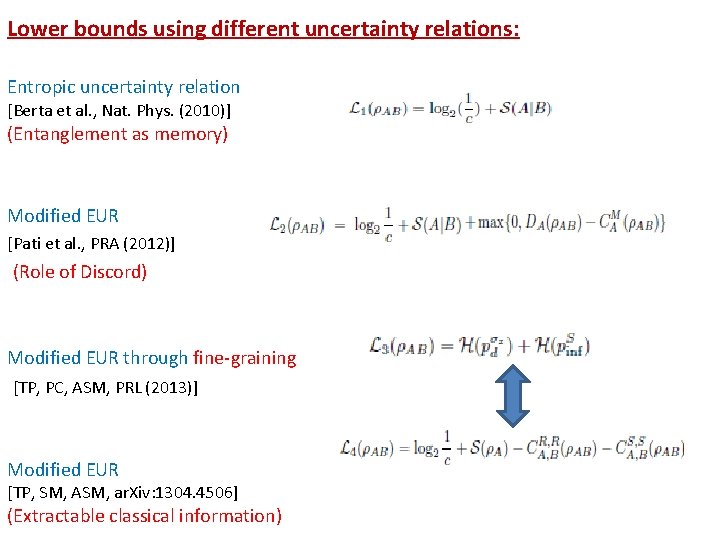
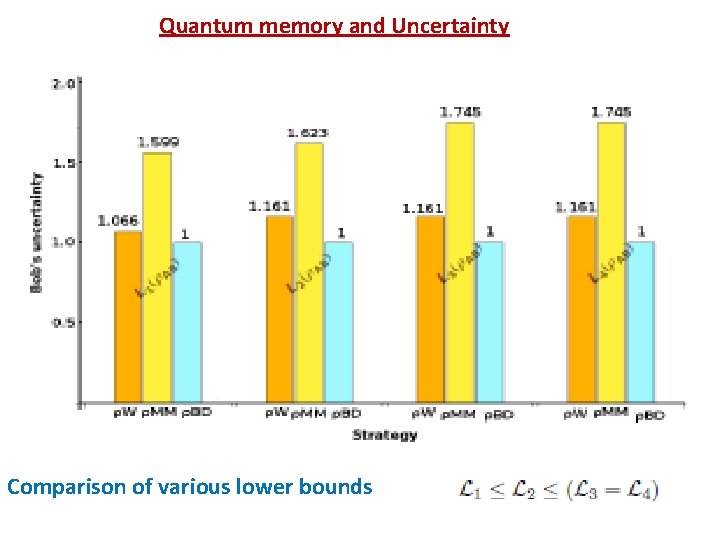
Lower bounds using different uncertainty relations: Entropic uncertainty relation [Berta et al. , Nat. Phys. (2010)] (Entanglement as memory) Modified EUR [Pati et al. , PRA (2012)] (Role of Discord) Modified EUR through fine-graining [TP, PC, ASM, PRL (2013)] Modified EUR [TP, SM, ASM, ar. Xiv: 1304. 4506] (Extractable classical information)

Quantum memory and Uncertainty L Comparison of various lower bounds

Summary • Various forms of uncertainty relations: Heisenberg, Robertson-Schrodinger, Entropic, Fine-grained, etc… Physical content of uncertainty relations (state (in)dependent bounds, correlations, relation with nonlocality, etc. • Applications: determination of purity/mixedness [TP, SM , ASM, PRA (2013)] • Demonstration of EPR paradox and steering [PC, ASM, GSA, PRA (2014)] • Reduction of uncertainty using quantum memory [Berta et al, Nat. Phys. (2010); Pati et al. , PRA (2012)] • Linking uncertainty with nonlocality; bipartite, tripartite systems, biased games [Oppenheim & Wehner, Science (2010); TP & ASM, PRA (2012); AD, TP, ASM, PRA (2013)] • Fine-graining leads to optimal lower bound of uncertainty in the presence of quantum memory [TP, PC, ASM, PRL (2013)]; Application in privacy of quantum key distribution