Quantum Walks Quantum Gates and Quantum Computers Andrew

Quantum Walks, Quantum Gates, and Quantum Computers Andrew Hines P. C. E. Stamp [Palm Beach, Gold Coast, Australia]

Motivation • Algorithms • Implementations • Decoherence and error-correction Bell’s Beach, Torquay, Australia]

Overview I. Background • Quantum Walks – simple & composite • Universality & Quantum Circuits II. Mappings • Quantum walks, qubit representations & implementations • Quantum Walks $ qubit Hamiltonians $ quantum circuits III. Decoherence • Decoherence models: implementation dependent • Example – quantum walk on hypercube [Duranbah, Gold Coast, Australia] Spin, Charge and Topology, Banff, August 2005

Background Quantum Walks [Great Barrier Reef, Cairns]

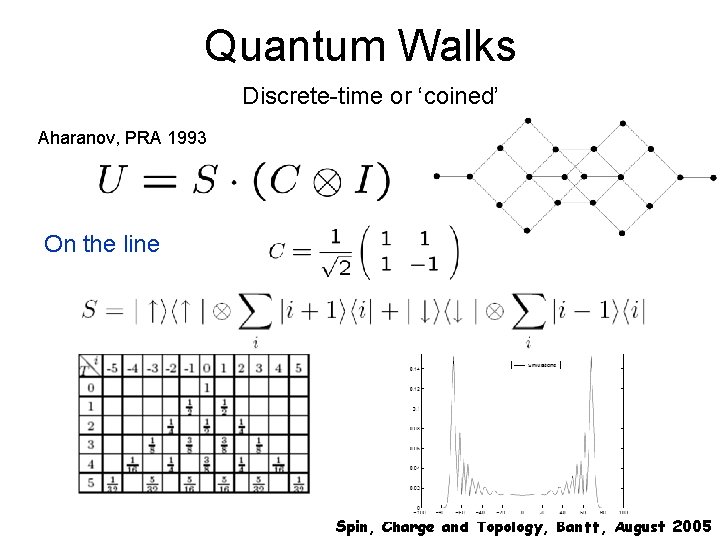
Quantum Walks Discrete-time or ‘coined’ Aharanov, PRA 1993 On the line Spin, Charge and Topology, Banff, August 2005

Quantum Walks Continuous-time Fahri & Guttman, PRA 1998 Childs et al. Hamiltonian is essentially the adjacency matrix for the corresponding graph, each node corresponding to an orthonormal basis state. Spin, Charge and Topology, Banff, August 2005

Quantum Walks Generalised 1. Simple quantum walk 2. Composite quantum walk Spin, Charge and Topology, Banff, August 2005

Background Quantum Circuits [The 12 Apostles, Great Ocean Road, Victoria

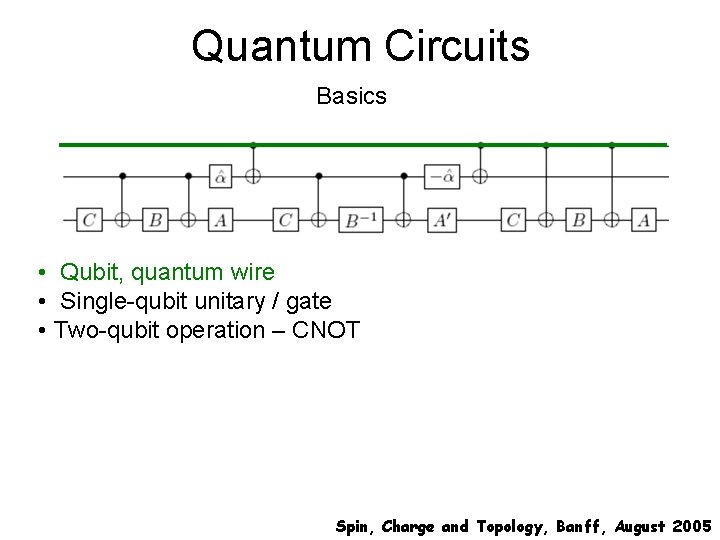
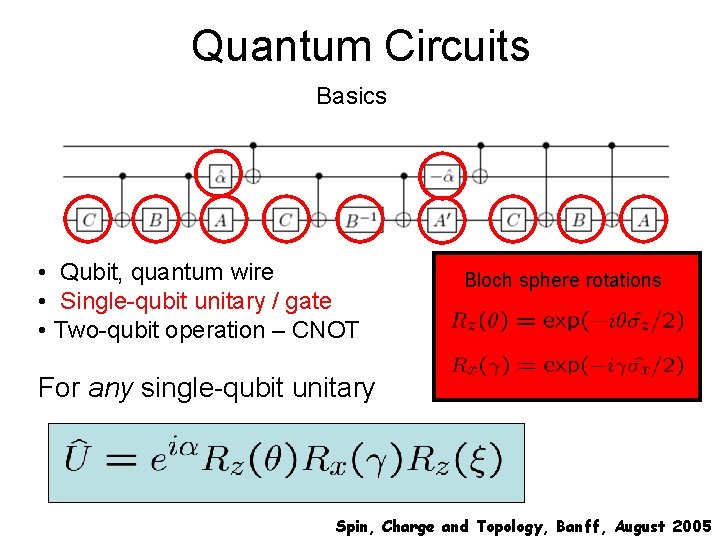
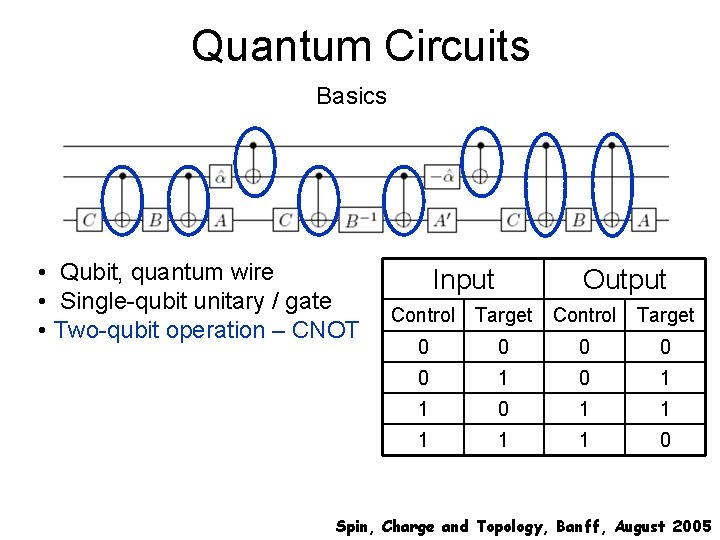
Quantum Circuits Basics • Qubit, quantum wire • Single-qubit unitary / gate • Two-qubit operation – CNOT Spin, Charge and Topology, Banff, August 2005

Quantum Circuits Basics • Qubit, quantum wire • Single-qubit unitary / gate • Two-qubit operation – CNOT Bloch sphere rotations For any single-qubit unitary Spin, Charge and Topology, Banff, August 2005

Quantum Circuits Basics • Qubit, quantum wire • Single-qubit unitary / gate • Two-qubit operation – CNOT Input Output Control Target 0 0 0 1 1 1 0 Spin, Charge and Topology, Banff, August 2005

Mappings Quantum Walks to Quantum circuits [Broadbeach, Queensland]

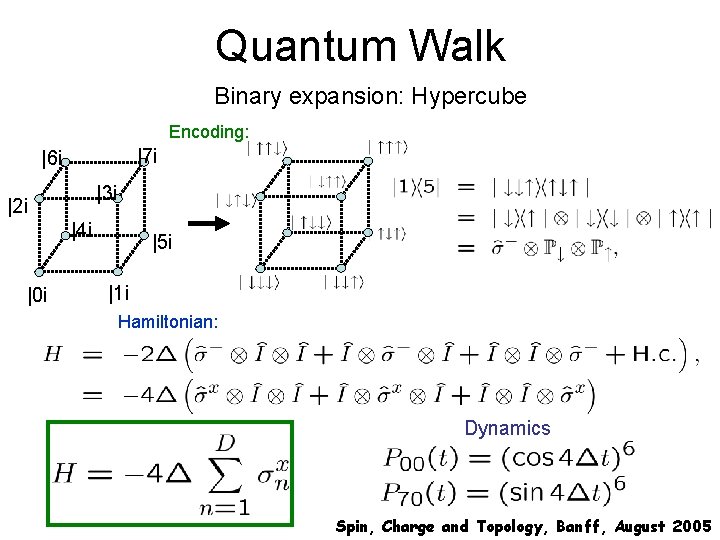
Quantum Walk Encoding QW in multi-qubit states 1) Single-excitation encoding • • jth spin N qubits = N nodes Hamiltonian operators: Walk in physical space not an efficient encoding, but may be easier to implement operations 2) Binary-expansion encoding { • N qubits = 2 N nodes • Walk in information space • efficient encoding, but dynamics can be more difficult to implement Spin, Charge and Topology, Banff, August 2005

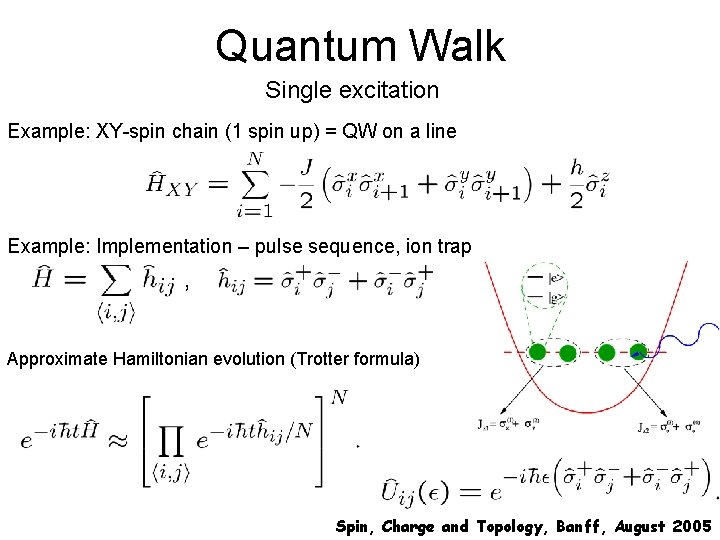
Quantum Walk Single excitation Example: XY-spin chain (1 spin up) = QW on a line Example: Implementation – pulse sequence, ion trap , Approximate Hamiltonian evolution (Trotter formula) Spin, Charge and Topology, Banff, August 2005

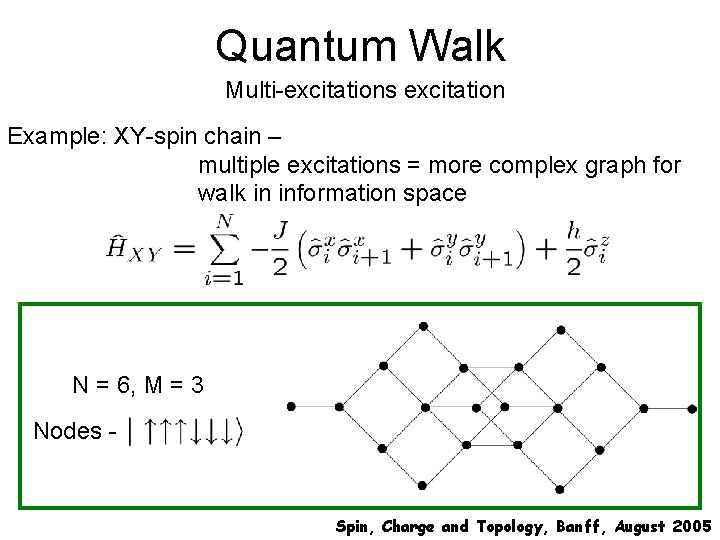
Quantum Walk Multi-excitations excitation Example: XY-spin chain – multiple excitations = more complex graph for walk in information space N = 6, M = 3 Nodes - Spin, Charge and Topology, Banff, August 2005

Quantum Walk Binary expansion: Hypercube Encoding: |7 i |6 i |3 i |2 i |4 i |0 i |5 i |1 i Hamiltonian: Dynamics Spin, Charge and Topology, Banff, August 2005

QW to gates Examples: The line Encoding: Hamiltonian: Simulation of evolution: Quantum circuit: Spin, Charge and Topology, Banff, August 2005

QW to gates Examples: The line Components Generalise to a hyperlattice, where each line represents a dimension. It turns out that `lines’ do not interact, so can simulate QW on arbitrary dimensional hyperlattice Spin, Charge and Topology, Banff, August 2005

Mappings Quantum circuits to Quantum Walks [Banff]

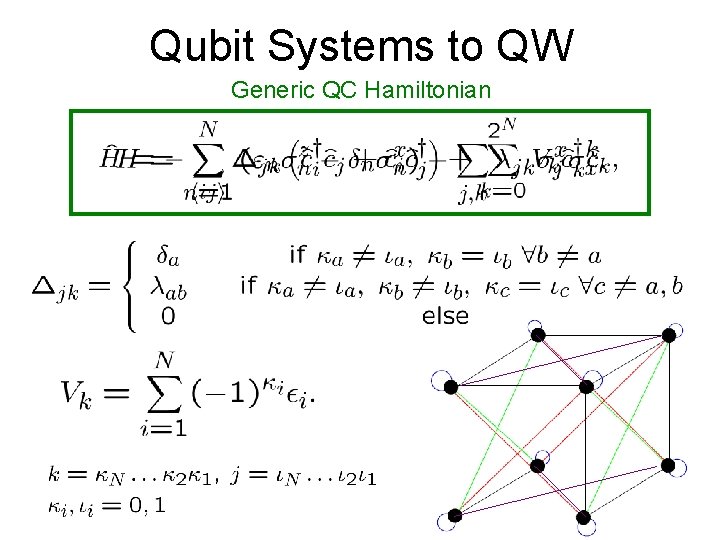
Qubit Systems to QW Generic QC Hamiltonian

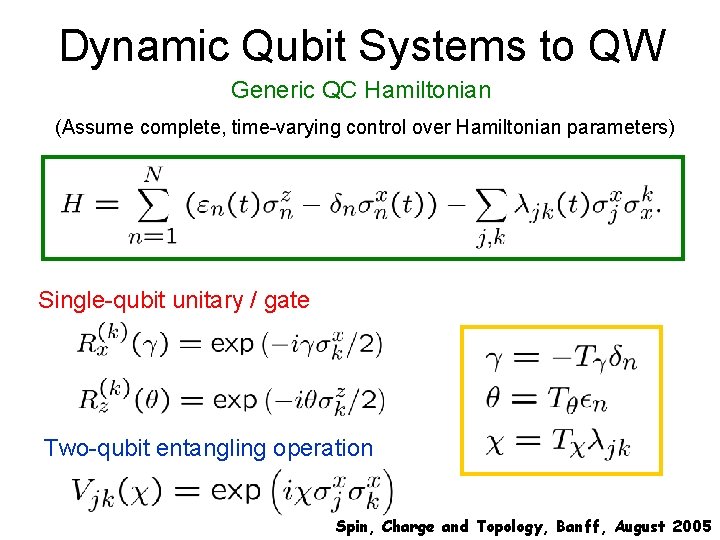
Dynamic Qubit Systems to QW Generic QC Hamiltonian (Assume complete, time-varying control over Hamiltonian parameters) Single-qubit unitary / gate Two-qubit entangling operation Spin, Charge and Topology, Banff, August 2005

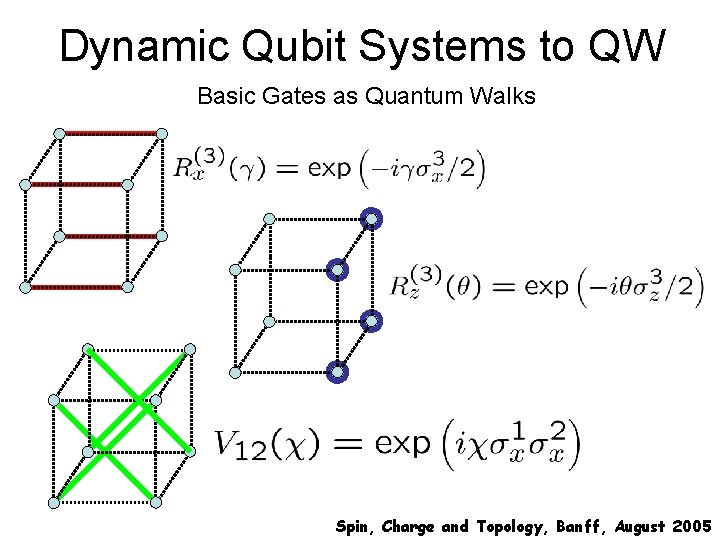
Dynamic Qubit Systems to QW Basic Gates as Quantum Walks Spin, Charge and Topology, Banff, August 2005

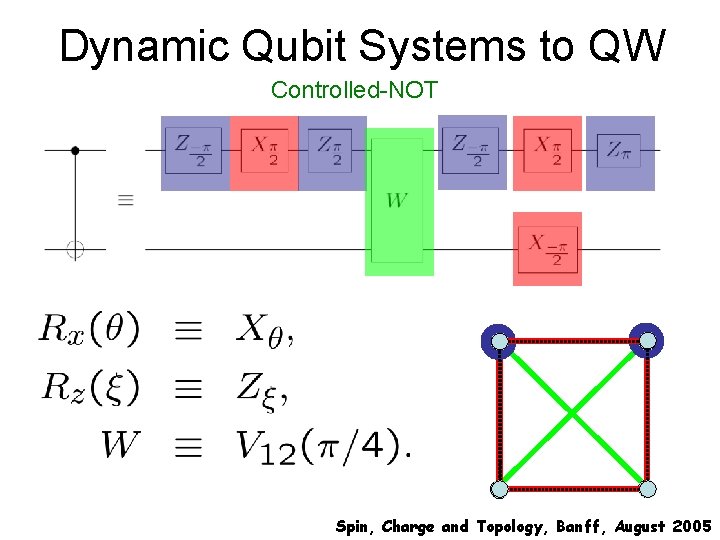
Dynamic Qubit Systems to QW Controlled-NOT Spin, Charge and Topology, Banff, August 2005

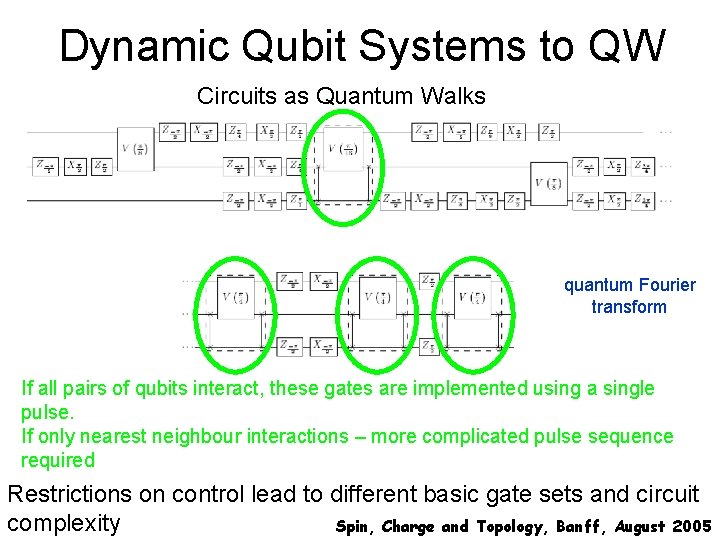
Dynamic Qubit Systems to QW Circuits as Quantum Walks quantum Fourier transform If all pairs of qubits interact, these gates are implemented using a single pulse. If only nearest neighbour interactions – more complicated pulse sequence required Restrictions on control lead to different basic gate sets and circuit complexity Spin, Charge and Topology, Banff, August 2005

Decoherence Models & a simple example [Wreck Beach, Vancouver]

Decoherence Error Models Local, independent error model (Pauli errors), dissipation & dephasing (master equation) Environments Oscillator bath Spin bath Specific form of errors/environmental couplings must depend upon what physical system the walk Hamiltonian is implemented with or describing. Spin, Charge and Topology, Banff, August 2005

Decoherence Quantum Walk on Hypercube Alagic & Russell, PRA 2006 |7 i |6 i |3 i |2 i |4 i |0 i Discrete-time model |5 i |1 i (Kendon & Tregenna, PRA 2004) POVM: Spin, Charge and Topology, Banff, August 2005

Decoherence Quantum Walk on Hypercube |7 i |6 i |3 i |2 i |4 i Continuous-time limit: |0 i Time-step ! 0 probability p ! 0 |5 i |1 i Rate p/ ! (constant) Spin, Charge and Topology, Banff, August 2005

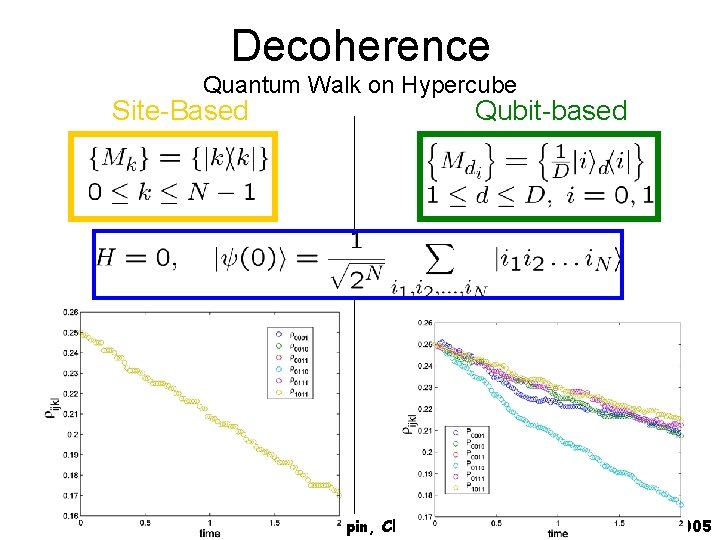
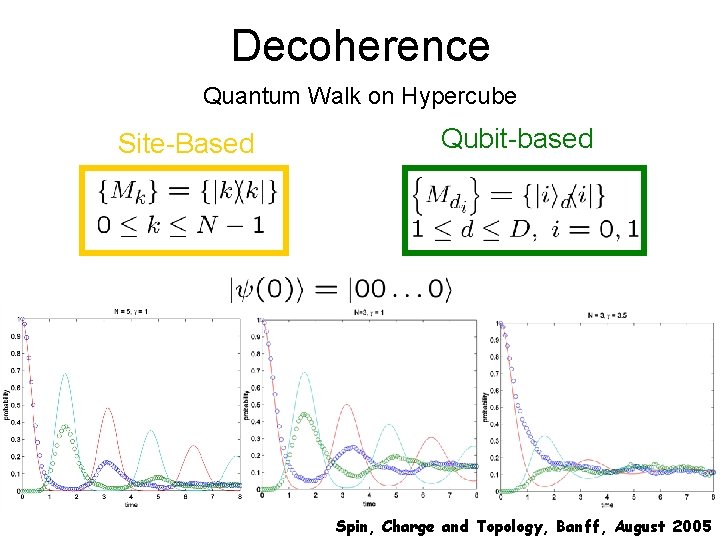
Decoherence Quantum Walk on Hypercube Site-Based Qubit-based Spin, Charge and Topology, Banff, August 2005

Decoherence Quantum Walk on Hypercube Site-Based Qubit-based Spin, Charge and Topology, Banff, August 2005

Thank you (Australian wildlife, being eaten by Dusty the cattle dog)