Quantum walks Definition and applications Ashley Montanaro Talk

Quantum walks: Definition and applications Ashley Montanaro

Talk structure n Introduction to quantum walks n Defining a quantum walk ¨. . . on the line ¨. . . on undirected graphs NEW ¨. . . on directed graphs n Applications of quantum walks

What are quantum walks? n A random walk is the simulation of the random movement of a particle around a graph n A quantum walk is the same – but with a quantum particle ¨ n not the same as running a normal random walk algorithm on a quantum computer Random walks are a useful model for developing classical algorithms; quantum walks provide a new way of developing quantum algorithms ¨ which is particularly important because producing new quantum algorithms is so hard

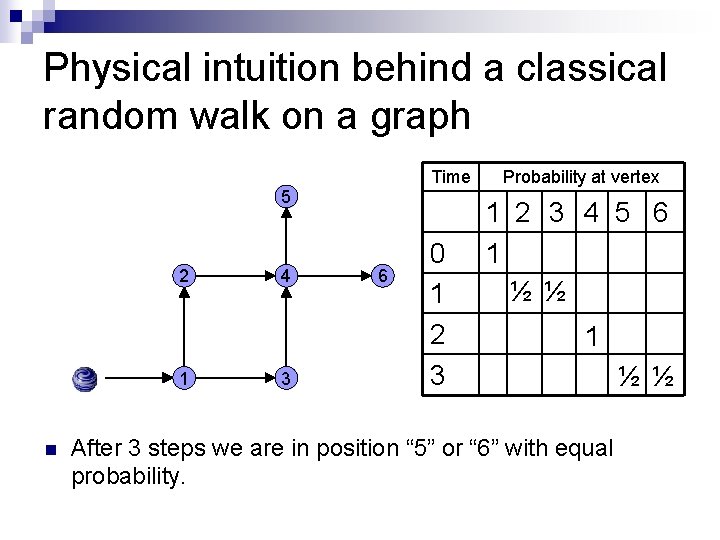
Physical intuition behind a classical random walk on a graph Time 5 2 1 n 4 3 6 0 1 2 3 Probability at vertex 1 2 3 4 5 6 1 ½½ 1 After 3 steps we are in position “ 5” or “ 6” with equal probability. ½½

Physical intuition behind a quantum walk on a graph Light detectors Mirror 5 2 6 4 1 3 Half-silvered mirror

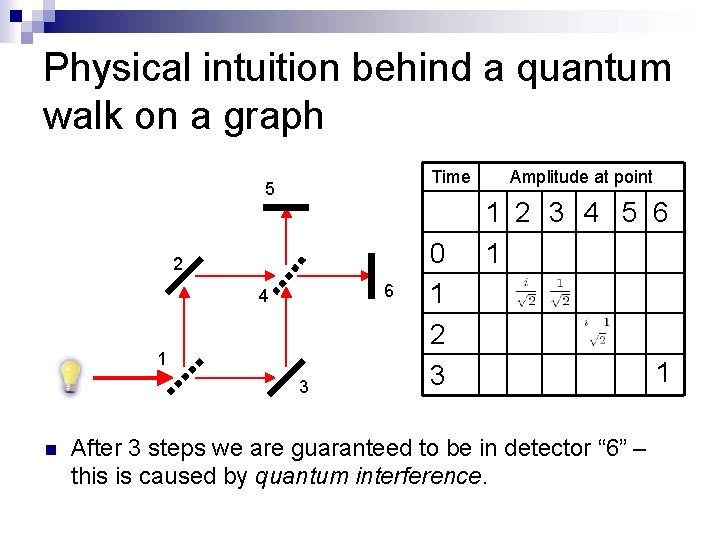
Physical intuition behind a quantum walk on a graph Time 5 2 6 4 1 3 n 0 1 2 3 Amplitude at point 1 2 3 4 5 6 1 After 3 steps we are guaranteed to be in detector “ 6” – this is caused by quantum interference. 1

Mathematical definition of a random walk n Express a classical random walk as a matrix W of transition probabilities ¨ n 2 4 1 3 where the entries in each column sum to 1 Express a position as a column vector v n Performing a step of the walk corresponds to pre-multiplying v by W n Performing n steps of the walk corresponds to pre-multiplying v by Wn =

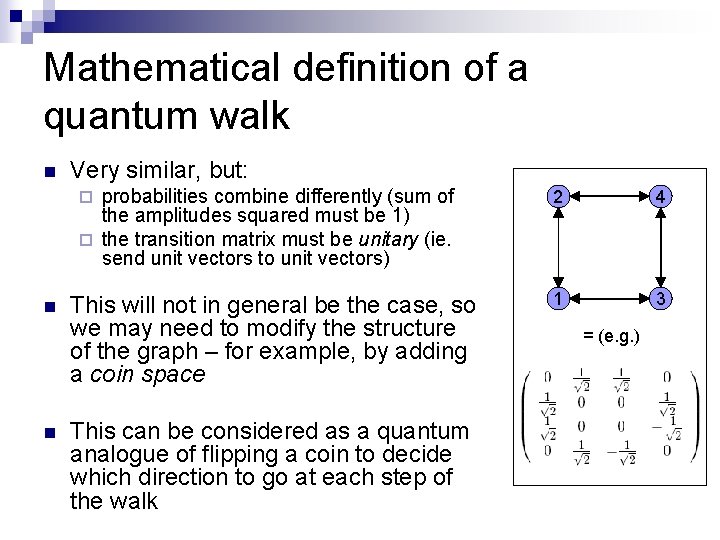
Mathematical definition of a quantum walk n Very similar, but: probabilities combine differently (sum of the amplitudes squared must be 1) ¨ the transition matrix must be unitary (ie. send unit vectors to unit vectors) ¨ n n This will not in general be the case, so we may need to modify the structure of the graph – for example, by adding a coin space This can be considered as a quantum analogue of flipping a coin to decide which direction to go at each step of the walk 2 4 1 3 = (e. g. )

Classical random walk on the line n Consider a walk on the following simple infinite graph: n Versions of this walk are useful models for many random processes n When the walker has equal probability to move left or right, it’s well-known that the average distance from the start position after time n is sqrt(n) n But we can define a quantum walk on the same graph with different behaviour: an average distance of n

Quantum walk on the line n We have two quantum registers: a coin register holding |L or |R , and a position register |p n Our walk operation is a coin flip followed by a shift n ¨ coin flip: send ¨ shift: send |L + i|R , |R i|L + |R |L |p-1 |R |p+1 These are both unitary operations, and hence their combination is too so, together, they provide a way of defining a quantum walk on the line ¨ there are other ways – e. g. the continuous-time formulation of quantum walks ¨

A few iterations of the walk on the line 1. start |R |0 2. coin (i|L + |R )|0 shift i|L |-1 + |R |1 3. coin (i|L - |R )|-1 + (i|L + |R )|1 shift i|L |-2 - |R |0 + i|L |0 + |R |2 4. coin (i|L - |R )|-2 + (i|L + |R )|2 shift i|L |-3 - |R |-1 + i|L |1 + |R |3 Equal probability to be at |-3 , |-1 , |1 or |3 - whereas classical random walk favours |-1 , |1

Classical vs. quantum walk on the line Running a classical walk on the line results in a probability distribution like: position Whereas running this quantum walk for the same number of steps gives: The peaks and troughs in this graph are caused by quantum interference.

Quantum walks on undirected graphs n Consider a d-regular graph G (each vertex has d arcs leaving it) n We can label each arc and choose between them using a d-dimensional “coin” ¨ A variety of coin operators can be used: we usually pick one to mix between all arcs equally n As before, one step of the walk consists of a coin flip followed by a shift n An irregular graph can be handled using a different coin for each vertex of a different degree ¨ or other methods. . .

Behaviour of quantum walks on undirected graphs n We can define quantum equivalents of the mixing time and hitting time of a walk n The mixing time of a random walk is the time it takes to converge to a limiting distribution ¨ n Quantum walks have quadratically faster mixing time for any undirected graph The hitting time is the time it takes to reach a given vertex On certain graphs, quantum walks have exponentially faster hitting time ¨ Open question: for which graphs is this true? ¨

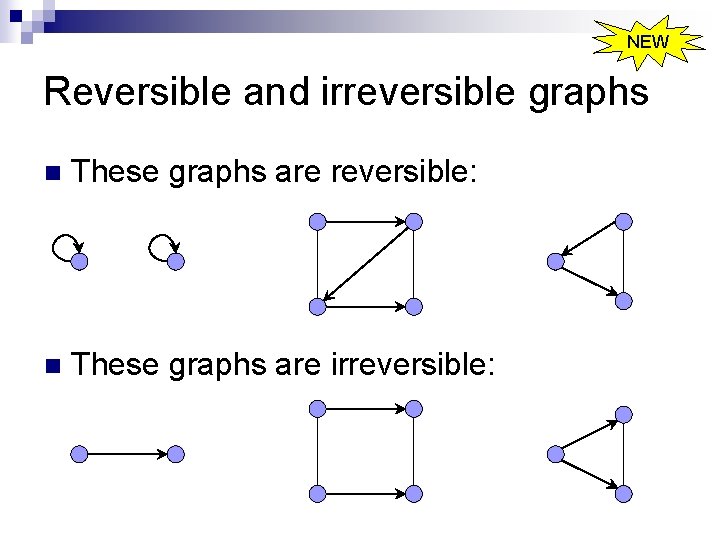
NEW Quantum walks on directed graphs n A quantum walk can be defined on any undirected graph, with the use of a suitable coin n But it turns out that not all directed graphs support the idea of a quantum walk: only reversible ones do a reversible graph is a graph where, if you can get from a to b, you can get from b to a ¨ each component of such graphs is strongly connected ¨ compare the idea that quantum computers have to be reversible ¨ n Quantum walks defined on irreversible graphs will not respect the structure of the graph: there will be some possibility to traverse arcs in the “wrong direction”

NEW Reversible and irreversible graphs n These graphs are reversible: n These graphs are irreversible:

Implications for translation of classical algorithms n NEW Many classical algorithms can be represented as a random walk on a directed graphs with sinks – the idea is to find a sink, which represents a solution to a problem ¨ e. g. Schöning’s random walk algorithm for SAT n A quantum walk cannot be defined on these graphs; this suggests that there is no easy translation of these algorithms into a quantum walk form n However, it is possible to produce a quantum walk which is “like” the original random walk in the sense that, after a long period of time, it has a high probability of ending up in a sink

Applications of quantum walks n Quantum network routing ¨ n Quantum walk search algorithm ¨ n Shenvi, Kempe, Whaley, 2002 Element distinctness ¨ n Kempe, 2002 Ambainis, 2004 Applications of element distinctness Magniez, Santha, Szegedy, 2003 ¨ Buhrmann, Spalek, 2004 ¨

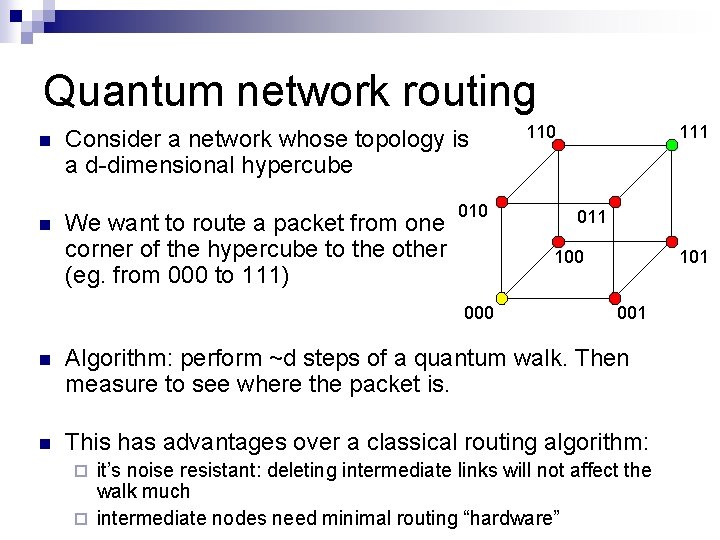
Quantum network routing n Consider a network whose topology is a d-dimensional hypercube n We want to route a packet from one corner of the hypercube to the other (eg. from 000 to 111) 010 111 011 100 000 101 001 n Algorithm: perform ~d steps of a quantum walk. Then measure to see where the packet is. n This has advantages over a classical routing algorithm: it’s noise resistant: deleting intermediate links will not affect the walk much ¨ intermediate nodes need minimal routing “hardware” ¨

Quantum walk search algorithm n Consider the unstructured search problem: given a function f(x) = { 1 if x = a, 0 otherwise } find the “marked” element a, where 0 a 2 n-1. n Grover’s algorithm can solve this in O(2 n/2) queries on a quantum computer, whereas a classical computer needs at least W(2 n) queries n Can we produce a quantum walk algorithm that requires the same (optimal) number of queries? ¨ this may be easier to implement, or provide a better model for searching a “real” database

Quantum walk search algorithm (2) n We perform a quantum walk on the hypercube of dimension n each vertex, labelled by an n-bit string, corresponds to a possible input to the oracle ¨ each vertex has n neighbours ¨ n Our walk consists of a combination of a coin flip and a shift, as before ¨ n Identify each of the n coin states with each neighbour of a vertex Use a “marking” coin operator ¨ ¨ When at an unmarked vertex, pick a coin state randomly When at the marked vertex, stay in the same coin state

Quantum walk search algorithm (3) n Start with a superposition over all vertices n If we run the walk for O(2 n/2) steps, can prove that there is a high probability it will “home in” on the marked vertex ¨ in fact, there’s a general result stating that “perturbed” walks like this will always find one of the marked elements n We then simply measure the position and we’ve found the marked item

Element distinctness n Problem: does a (multi-)set S of N elements contain any duplicate elements? n Call reading an element from the set a query n Clearly, classically we need N queries to answer the question with certainty n It turns out that a quantum walk algorithm can solve the problem in O(N 2/3) queries ¨ which has been proven to be optimal

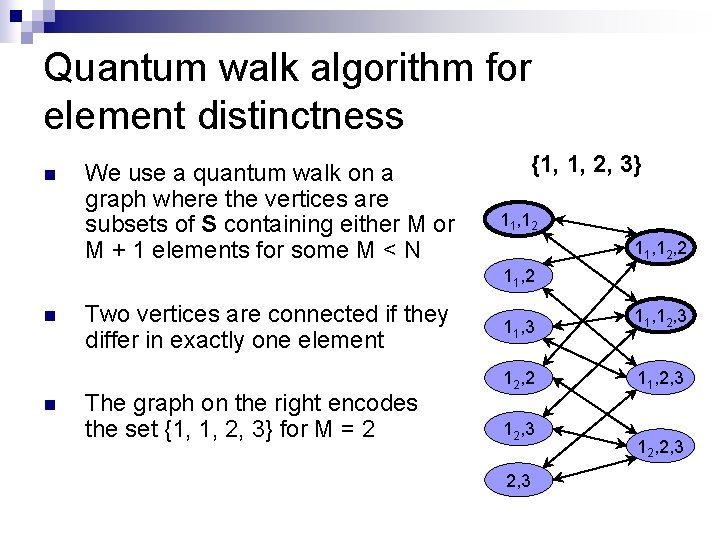
Quantum walk algorithm for element distinctness n We use a quantum walk on a graph where the vertices are subsets of S containing either M or M + 1 elements for some M < N {1, 1, 2, 3} 11, 12, 2 11, 2 n n Two vertices are connected if they differ in exactly one element The graph on the right encodes the set {1, 1, 2, 3} for M = 2 11, 3 12, 2 12, 3 11, 2, 3 12, 2, 3

Quantum walk algorithm for element distinctness (2) n Basic walk algorithm: start with some subset S’ S (where |S’| = M) 2. check whether S’ contains any duplicates (needs O(M) queries) 3. if not, change to a different subset S’’ that differs in exactly one element 4. check S’’ for duplicates (needs 1 query) 5. repeat steps 3 and 4 until a duplicate is found 1. n Because this is a quantum walk, we can start with a superposition of all M-subsets

Analysis of quantum walk n In total, we need (M + r) queries, where M is the number of elements in the initial subset ¨ r is the number of steps of the quantum walk ¨ n It turns out that if we pick M = N 2/3, then a solution can be found with high probability in r = N 1/3 steps of the walk resulting in O(N 2/3) queries in total ¨ it also turns out that the number of non-query operations required is small, so the query complexity is a good measure of the time complexity ¨ n Note that this algorithm requires a significant amount of space – enough to store O(N 2/3) elements

Applications of element distinctness n Using element distinctness as a subroutine, quantum walk algorithms have been developed to solve other problems: ¨ finding a triangle in a graph with n vertices in time O(n 1. 3) ¨ verifying matrix multiplication (testing if A*B = C for some n*n matrices A, B, C) in time O(n 1. 67) n The algorithm has also been generalised to solve the problem of finding any subset that has a given property find (a, b) such that (f(a), f(b)) P, where P is some property ¨ i. e. :

Conclusions and further reading n Quantum walks can be defined on any undirected graph, and on reversible directed graphs. n Quantum walks are a way to develop quantum algorithms that outperform their classical counterparts. n Further reading (on www. arxiv. org): “Quantum walks and their algorithmic applications”, A. Ambainis, quant-ph/0311001 ¨ “Quantum random walks – an introductory overview”, J. Kempe, quant-ph/0303081 ¨ “Quantum walks on directed graphs”, A. Montanaro, quantph/0504116 ¨