Prrequis la statistique 2014 1 Echauffement l Compltez

Prérequis à la statistique 2014 1

Echauffement : l Complétez avec la bonne unité 1. Une plaquette de beurre a une masse de 250 U. 2. Cette bouteille de vin contient 75 U. 3. La distance entre Calais et Marseille est d'environ 1000 U. 4. Cette petite ampoule de médicament contient environ 1 U. 5. Ce camion transporte 38 U de marchandises. 6. Dans ce comprimé, il y a 100 U de produit actif. 7. Cette voiture a une masse de 1450 U. 8. Donnez-moi 100 U de bonbons. 9. Trace un cercle de 5 U de rayon. Son aire vaudra πR² U. 10. Ma cuve à mazout a un volume de 1 U. 2

Echauffement : l Comparez ces mesures(<, >, =) a) 2. 5 km ? 1854 m b) 0. 125 km ? 99 m c) 1 g ? 743 mg d) 34250 m² ? 0. 3425 km² e) 18 cm³ ? 12500 mm³ f) 6. 25 kg/m³ ? 185 g/L g) 0. 7 hm² ? 700 m² h) 6 x 10 -2 cm³ ? 600 mg d’eau i) 3. 5 x 109 cm³ ? 2 dam³ j) 2. 6 x 100 hl ? 130 dm³ 3

Solutions l Complétez avec la bonne unité 1. Une plaquette de beurre a une masse de 250 g. 2. Cette bouteille de vin contient 75 cl. 3. La distance entre Calais et Marseille est d'environ 1000 km. 4. Cette petite ampoule de médicament contient environ 1 ml (= 1 cm³). 5. Ce camion transporte 38 t de marchandises. 6. Dans ce comprimé, il y a 100 mg de produit actif. 7. Cette voiture a une masse de 1450 kg. 8. Donnez-moi 100 g de bonbons. 9. Trace un cercle de 5 cm de rayon. Son aire vaudra πR² cm². 10. Ma cuve à mazout a un volume de 1 m³. 4

Solutions l Comparez ces mesures(<, >, =) a) 2. 5 km > 1854 m b) 0. 125 km > 99 m c) 1 g > 743 mg d) 34250 m² < 0. 3425 km² e) 18 cm³ > 12500 mm³ f) 6. 25 kg/m³ < 185 g/L g) 0. 7 hm² > 700 m² h) 6 x 10 -2 cm³ < 600 mg d’eau i) 3. 5 x 109 cm³ > 2 dam³ j) 2. 6 x 100 hl > 130 dm³ 5

Fractions l Fractions ordinaires – Comparaison de fractions l l – Simplification l l – – l l Règles de priorité de calcul Ne jamais diviser par zéro Fractions généralisées Conversions de fractions en nombres décimaux – 6 Changements apportés à une fraction Simplification des fractions Réduction au même dénominateur Opérations sur les fractions l l Avec l'unité Entre elles Pourcentage

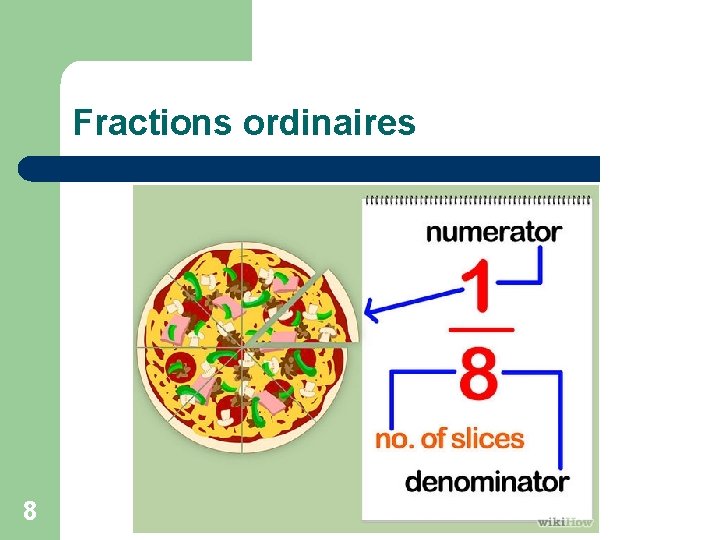
Fractions ordinaires l Prendre les ¾ d’une grandeur 2 opérations 1. Diviser la grandeur en 4 parties égales et 2. Multiplier la grandeur par 3. l Résultat = partie d'une grandeur = fraction = l l 7 Nombre qui indique en combien de parties égales on a divisé l'unité = le dénominateur (4) Nombre qui indique combien on a pris de ces parties = le numérateur (3).

Fractions ordinaires 8

Fractions ordinaires 9

Fractions ordinaires 10

Fractiooooons ! 11

Fractions ordinaires : comparaison l 12 Comparaison de fractions par rapport à l’unité – < 1 quand numérateur < dénominateur – > 1 quand numérateur > dénominateur

Fractions ordinaires : comparaison l 13 Comparaison de fractions entre elles – Si dénominateurs égaux, la > est celle qui a le > numérateur – Si numérateurs égaux, la > est celle qui a le < dénominateur – Si numérateurs et dénominateurs différents réduire au même dénominateur

Fractions ordinaires : simplifications l Convertir n'importe quel nombre en fraction de dénominateur donné : – 14 multiplier numérateur par nombre choisi comme dénominateur :

Fractions ordinaires : simplifications l Comment simplifie-t-on une fraction ? – diviser les deux termes par un même nombre, si possible – Fraction irréductible si on divise les 2 termes par leur PGCD l 15 (ci-dessus, PGCD = 10 x 6 = 60)

Fractions ordinaires : réduction au même dénominateur l Pourquoi réduire au même dénominateur ? – l 16 Quelle différence y a-t-il entre 3/4 et 4/5 de mètre ? l 3/4 m = 75 cm et 4/5 m = 80 cm 5 cm l 3/4 m = 75/100 m et 4/5 m = 80/100 m 5/100 m Réduire plusieurs fractions au même dénominateur = transformer ces fractions en d'autres, respectivement égales, qui ont toutes le même dénominateur.

Fractions ordinaires : réduction au même dénominateur l Règle : Pour réduire plusieurs fractions au plus petit dénominateur commun : – – – 17 1. on les rend irréductibles ; 2. PPCM des dénominateurs = plus petit dénominateur recherché ; 3. multiplier les deux termes de chacune des fractions par le nombre de fois que son dénominateur est contenu dans le PPCM.

Fractions ordinaires : réduction au même dénominateur l Règle : Pour réduire plusieurs fractions au plus petit dénominateur commun : – – – 18 1. on les rend irréductibles ; 2. PPCM des dénominateurs = plus petit dénominateur recherché ; 3. multiplier les deux termes de chacune des fractions par le nombre de fois que son dénominateur est contenu dans le PPCM.

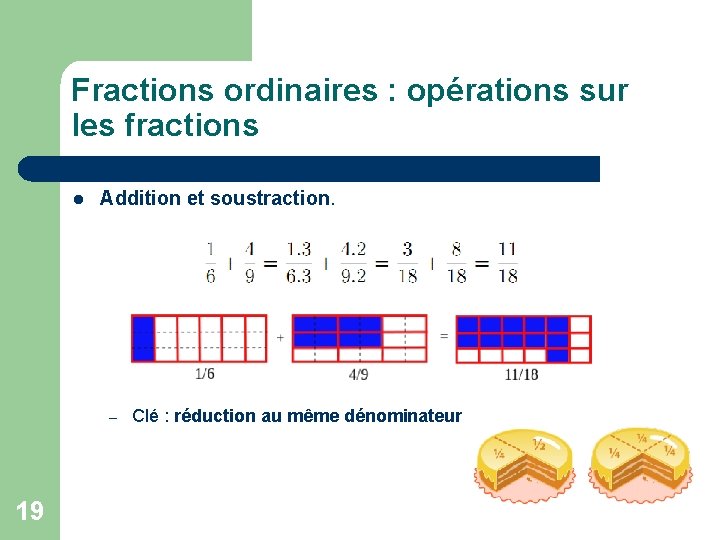
Fractions ordinaires : opérations sur les fractions l Addition et soustraction. – 19 Clé : réduction au même dénominateur

Fractions ordinaires : opérations sur les fractions l Multiplication : – Clé : multiplier l l – 20 numérateurs entre eux et dénominateurs entre eux. Marche à tous les coups :

Fractions ordinaires : opérations sur les fractions l Division d’une fraction par un nombre : – Clé : l l 21 diviser numérateur par le nombre ou multiplier dénominateur par le nombre

Fractions ordinaires : opérations sur les fractions l 22 Division d’une fraction par une fraction : – Clé : multiplier dividende par inverse diviseur – Remarque :

Fractions ordinaires : opérations sur les fractions l Puissances et racines : – 23 Remarque, racine vue comme puissance :

Fractions ordinaires : opérations sur les fractions 24 l Priorités de calcul l 1. calculs entre parenthèses (ou crochets) prioritaires sur calculs situés en dehors de ces parenthèses ; barre de fraction ou racine = parenthèse ; l 2. exposants prioritaires sur multiplications, divisions, additions et soustractions ; l 3. multiplications et divisions prioritaires sur additions et soustractions.

Fractions ordinaires : opérations sur les fractions l Division par zéro – plus les morceaux d'une tarte sont petits, plus ils sont nombreux plus les morceaux sont petits, plus il y en aura. ne JAMAIS diviser par zéro. – Remarque : l 25 l ± ? infini ( ) n’est pas le nombre le plus grand car, s'il est un nombre, on peut lui ajouter 1 et ce n’est donc plus le plus grand ( + 1 > ? ).

Fractions l Fractions ordinaires – Comparaison de fractions l l – Simplification l l – – l l Règles de priorité de calcul Ne jamais diviser par zéro Fractions généralisées Conversions de fractions en nombres décimaux – 26 Changements apportés à une fraction Simplification des fractions Réduction au même dénominateur Opérations sur les fractions l l Avec l'unité Entre elles Pourcentage

Fractions généralisées 27 l Exemples : l obéissent aux mêmes lois que les fractions ordinaires

Fractions généralisées l Fractions égyptiennes : l Pourquoi faire simple ? – N'importe quelle fraction était écrite par les anciens Égyptiens comme une l l 28 somme de fractions unitaires sans que deux de ces dénominateurs soient les mêmes.

Fractions l Fractions ordinaires – Comparaison de fractions l l – Simplification l l – – l l Règles de priorité de calcul Ne jamais diviser par zéro Fractions généralisées Conversions de fractions en nombres décimaux – 29 Changements apportés à une fraction Simplification des fractions Réduction au même dénominateur Opérations sur les fractions l l Avec l'unité Entre elles Pourcentage

Conversion de fractions en nombres décimaux l 30 on divise le numérateur par le dénominateur – condition pour qu'une fraction irréductible puisse être convertie en nombre décimal limité : son dénominateur ne contienne pas d'autres facteurs premiers que 2 et 5 – Au fait, c’est quoi un facteur premier ?

Conversion de fractions en nombres décimaux l facteur premier ? – factorisation en nombres premiers = écrire un entier naturel non nul sous forme d'un produit de nombres premiers – Exemple: Décomposition du nombre 240 en produit de facteurs premiers: l l l 31 240 = 2× 120 (2 = plus petit nombre premier qui divise 240) 120 = 2× 60 (2 = plus petit nombre premier qui divise 120) 60 = 2× 30 (2 = plus petit nombre premier qui divise 60) 30 = 2× 15 (2 = plus petit nombre premier qui divise 30) 15 = 3× 5 (3 = plus petit nombre premier qui divise 15) 5 = 5× 1 (5 = nombre premier décomposition terminée) 240 = 2 × 2 × 3 × 5 = 23 × 31 × 51

Conversion de fractions en nombres décimaux l 32 fraction non convertible en nombre décimal limité nombre décimal périodique. – nombre décimal mixte : – Cas particulier :

Fractiooooons ! 33