La statistique Non Cest facile La statistique est

La statistique ? ? Non ! C’est facile

La statistique est un outil qui permet : d’organiser, de décrire, d’estimer, de comparer, de prédire et de trouver des liens de causalité.

La variabilité Qu’est ce que la variabilité ? >2 000 de pages Web « la variabilité du temps et du climat » , « la variabilité cardiaque au cours des cycles de sommeil chez l‘homme » , « la variabilité génétique » , « la variabilité des forces de réaction au sol » , « Modèles de la variabilité » , … D’où vient la variabilité ? Analytique, biologique, échantillonnage, … Qu’est ce qui est variable ? Une mesure, une variable aléatoire …

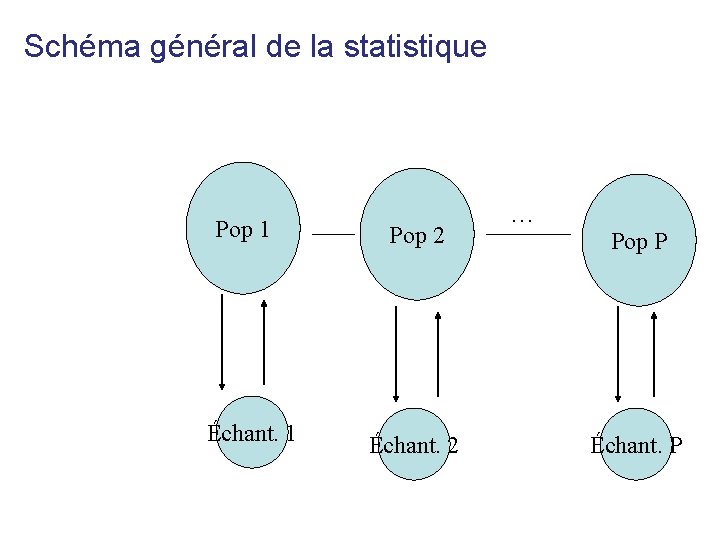
Schéma général de la statistique Pop 1 Échant. 1 Pop 2 Échant. 2 … Pop P Échant. P

Définitions et principes généraux des tests statistiques (1) Présentation générale Un test d’hypothèse est une règle de décision. La décision est un pari et comporte toujours des risques d’erreur. A partir des données d’un échantillon (observations), on doit rejeter ou non une hypothèse statistique faite sur une ou des populations, c’est à dire une hypothèse portant sur la nature d’une ou plusieurs distributions, ou sur les paramètres qui leur sont attachés.

Définitions et principes généraux des tests statistiques (2) Quelles hypothèses ? La démarche débute par l’établissement d’une hypothèse de travail. C’est cette hypothèse qui sera mise à l’épreuve, testée. Cette hypothèse s’appelle l’hypothèse nulle notée H 0. Le choix de H 0 est particulier : il est fonction de ce que l’on souhaite invalider (rejeter). On supposera que H 0 est vraie et qu’une valeur observée peu probable sous H 0 contredit H 0. Il y a une analogie avec le raisonnement par l’absurde en mathématiques.

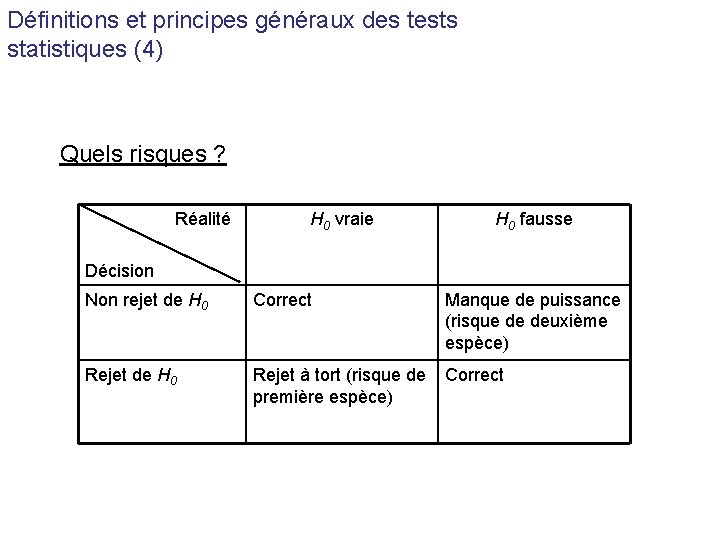
Définitions et principes généraux des tests statistiques (4) Quels risques ? Réalité H 0 vraie H 0 fausse Décision Non rejet de H 0 Correct Manque de puissance (risque de deuxième espèce) Rejet de H 0 Rejet à tort (risque de Correct première espèce)

Définitions et principes généraux des tests statistiques (5) Quels risques ? Le risque de première espèce est noté . Son interprétation est la suivante: une conclusion de rejet de l’hypothèse nulle étant un pari, le risque l’on prend en formulant ce pari doit être inférieur ou égal à , sinon, on ne le prend pas et on ne rejette pas l’hypothèse nulle. Le risque de deuxième espèce est noté . La puissance est définie comme = 1 -. On ne peut pas maîtriser simultanément les deux risques. Le premier est généralement considéré comme le plus lourd de conséquence et c’est ce risque de rejet à tort qui sera pris comme critère de la décision à l’issue de la procédure de test.

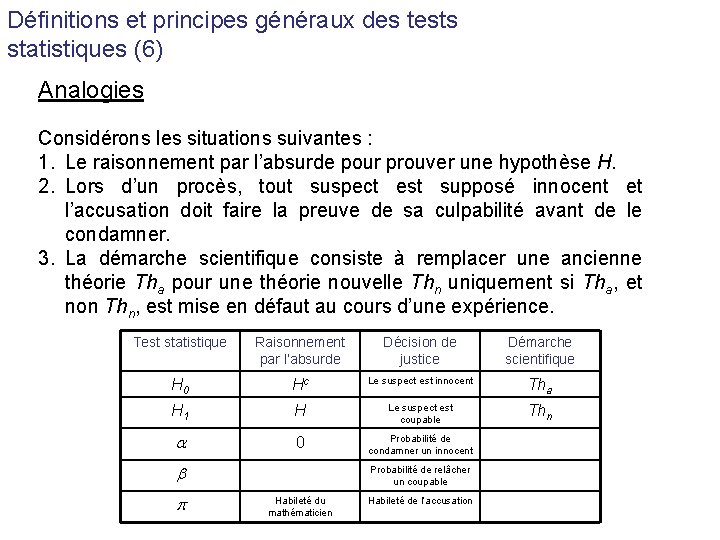
Définitions et principes généraux des tests statistiques (6) Analogies Considérons les situations suivantes : 1. Le raisonnement par l’absurde pour prouver une hypothèse H. 2. Lors d’un procès, tout suspect est supposé innocent et l’accusation doit faire la preuve de sa culpabilité avant de le condamner. 3. La démarche scientifique consiste à remplacer une ancienne théorie Tha pour une théorie nouvelle Thn uniquement si Tha, et non Thn, est mise en défaut au cours d’une expérience. Test statistique Raisonnement par l’absurde Décision de justice Démarche scientifique H 0 Hc Le suspect est innocent Tha H 1 H Le suspect est coupable Thn 0 Probabilité de condamner un innocent Probabilité de relâcher un coupable Habileté du mathématicien Habileté de l’accusation

Définitions et principes généraux des tests statistiques (7) Méthodologie générale Le principe est le suivant : on se place dans un espace « mathématique » abstrait (adapté au problème étudié) et on représente par deux points dans cet espace, d’une part l’hypothèse H 0 (faite sur une ou des populations), d’autre part l’échantillon observé. On définit un « écart » entre ces deux points, tobs, et on fixe un risque d’erreur . A ce risque correspond un écart critique t. Si tobs > t , on rejette l’hypothèse H 0, sinon, on ne la rejette pas. Zone de rejet (région critique) Zone de non rejet L’exécution d’un test codifié en trois étapes. H 0 t tobs

Définitions et principes généraux des tests statistiques (8) Première étape Devant une situation expérimentale et les données recueillies, on doit choisir : • Une hypothèse nulle H 0, • Un type de test statistique, • Un risque de première espèce . Le choix du type de test statistique implique le choix de la statistique de test T (qui est une variable aléatoire) et de la loi de cette variable aléatoire sous H 0. Il est donc nécessaire de connaître (même approximativement) la loi de probabilité de la statistique de test T lorsque l’hypothèse H 0 est vraie. PACES

Définitions et principes généraux des tests statistiques (9) Deuxième étape Il faut déterminer les valeurs dont la comparaison guidera la conclusion: • tobs est obtenu à partir des valeurs observées sur l’échantillon suivant une formule propre au test choisi : tobs est la valeur de la statistique de test T calculée sur l’échantillon observé, • t est lu dans une table statistique spécifique au test choisi.

Définitions et principes généraux des tests statistiques (10) Troisième étape Conclure : • si tobs est inférieur à t : on ne rejette pas H 0 • si tobs est supérieur à t : on rejette H 0. Zone de rejet (région critique) Zone de non rejet H 0 t tobs

Tests paramétriques pour variables quantitatives (1) Comparaison d’une moyenne observée à une valeur de référence Le test de Student On considère une population, sur laquelle est défini un caractère numérique distribué selon une loi normale . On dispose d’un échantillon de taille n, sur lequel on estime l’espérance µ par la moyenne observée et l’écart-type par S. L’hypothèse nulle H 0 à tester est H 0 : = 0, 0 étant une valeur donnée. La statistique , suit sous H 0 une loi de Student t est lu dans la table de la loi de Student à n-1 degrés de liberté.

Tests paramétriques pour variables quantitatives (2) Comparaison d’une moyenne observée à une valeur de référence Le test de l’écart réduit Pour n grand (n 30), il est raisonnable de considérer comme égal à la valeur estimée S. Dans ce cas (ou quand la variance est connue), on peut utiliser comme statistique de test : qui suit, sous H 0 une loi normale centrée réduite t est alors lu dans la table de la loi Rem : la loi de Student converge vers la loi normale centrée réduite lorsque n tend vers l’infini. Ce test n’est valable que si la variable aléatoire observée est de loi normale. On peut néanmoins l’utiliser pour une loi quelconque si n 30.

Tests paramétriques pour variables quantitatives (3) Exemple (test de Student ou de l’écart réduit) Données – Échantillon: 100 individus obèses (IMC>30) – Critère de jugement: glycémie = 1, 4 g/l, S = 0, 8 g/l – Question: ces individus présentent ils une glycémie normale (1 g/l) ? Problématique: Comparaison d’une moyenne à une valeur donnée Test: – Hypothèses • H 0: = 1 g/l • H 1: 1 g/l – Sous H 0, calcul de tobs = 5, – n 30 => t =1. 96 – On lit dans table => p-value<0, 001 Conclusion statistique: rejet de H 0 Conclusion clinique: l’échantillon présente une glycémie anormalement élevée

Tests paramétriques pour variables quantitatives (5) Comparaison de deux moyennes observées sur des échantillons indépendants Test de Student Deux populations de même variance 2 et de moyenne µ 1 et µ 2. La distribution de la variable, dans chacune des populations, suit une loi normale. L’hypothèse nulle H 0 à tester est H 0 : µ 1 = µ 2. On note m 1 et m 2 les estimations des moyennes µ 1 et µ 2, S 12 et S 22 celles des variances dans les deux échantillons. , où t est lu dans la table de la loi de Student à n 1+n 2 -2 degrés de liberté.

Tests paramétriques pour variables quantitatives (6) Exemple (test de Student) Données – 2 groupes de patients présentant un diabète de type 2: n 1=n 2=25 –Facteur étudié: hypoglycémiant (groupe 1) versus placebo (groupe 2) –Critères de jugement: glycémie m 1=1, 2 g/l , S 1=0, 5 g/l et m 2=1, 4 g/l, S 2=0, 8 g/l –Question: Le traitement hypoglycémiant est-il efficace? Problématique: comparaison de 2 moyennes observées sur 2 échantillons indépendants H 0: 1= 2 versus H 1: 1 2 Sous H 0, on suppose les variances statistiquement égales et que la glycémie suit une loi normale, tobs=1. 06 On lit t dans table de Student à 48 ddl , p-value>0, 05. Conclusion statistique: non rejet de H 0 Conclusion clinique: on ne met pas en évidence d’efficacité du traitement

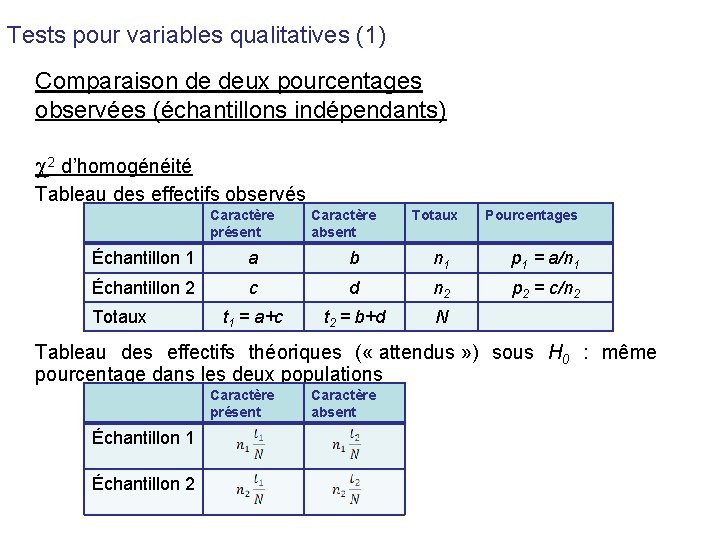
Tests pour variables qualitatives (1) Comparaison de deux pourcentages observées (échantillons indépendants) 2 d’homogénéité Tableau des effectifs observés Caractère présent Caractère absent Totaux Pourcentages Échantillon 1 a b n 1 p 1 = a/n 1 Échantillon 2 c d n 2 p 2 = c/n 2 t 1 = a+c t 2 = b+d N Totaux Tableau des effectifs théoriques ( « attendus » ) sous H 0 : même pourcentage dans les deux populations Caractère présent Échantillon 1 Échantillon 2 Caractère absent

Tests pour variables qualitatives (2) Comparaison de deux pourcentages observées (échantillons indépendants) 2 d’homogénéité La statistique de test une distance entre les deux tableaux. Oij est le nombre observé dans la case ij Eij est le nombre attendu sous H 0 de la case ij tobs = 2 obs = Sous H 0, 2 obs suit asymptotiquement une loi du 2 à 1 ddl. Quand 2 obs est grand, on rejette l’hypothèse nulle. L’utilisation de ce test impose que le nombre minimal des sujets dans le tableau théorique soit supérieur ou égal à 5.

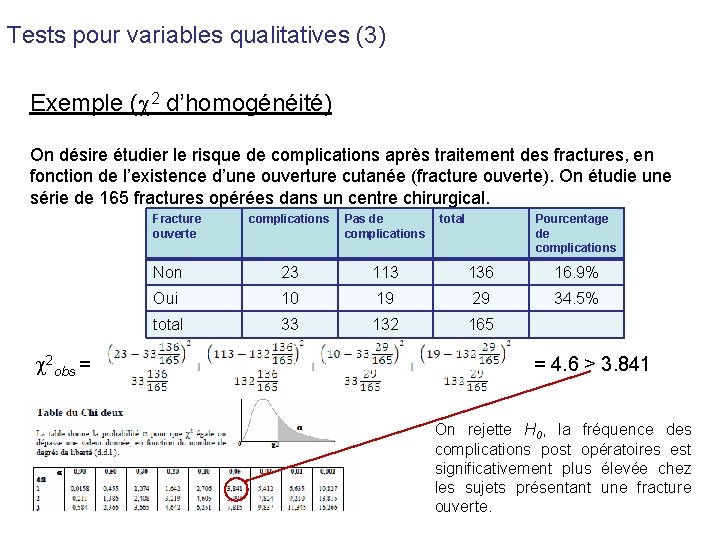
Tests pour variables qualitatives (3) Exemple ( 2 d’homogénéité) On désire étudier le risque de complications après traitement des fractures, en fonction de l’existence d’une ouverture cutanée (fracture ouverte). On étudie une série de 165 fractures opérées dans un centre chirurgical. Fracture ouverte 2 obs = complications Pas de complications total Pourcentage de complications Non 23 113 136 16. 9% Oui 10 19 29 34. 5% total 33 132 165 = 4. 6 > 3. 841 On rejette H 0, la fréquence des complications post opératoires est significativement plus élevée chez les sujets présentant une fracture ouverte.

Tests non paramétriques (3) Les rangs Sous l’hypothèse H 0, les individus devraient être rangés de façon aléatoire, les valeurs d’une série alternant avec celles de l’autre. Sous H 1, si les valeurs d’une séries à comparer sont en moyenne plus élevées, leurs rangs après classement sont en moyenne plus élevés. 1 2 3 4 5 6 7 8 8 10 11 12 Sous H 0 1 Sous H 1 2 5 6 7 8 9 10 11 12

Tests non paramétriques (4) Exemple introductif On veut comparer la distribution de deux échantillons (groupe 1 : 2, 1, 4 et groupe 2 : 5, 6). Le joueur Y a-t-il plus de chance que le joueur X ? Valeur : 1 2 4 5 6 Rang : 1 2 3 4 5 Groupe : 1 1 1 2 2 La somme des rangs pour l’échantillon du groupe 2 est Srg 2 = 4+5 = 9. 1 2 3 4 5 3 4 5 Srg. Y 6 6 5 Il y a =10 façons de choisir 2 nombres parmi 5. 7 8 9 L’hypothèse H 0 n’est pas rejetée au risque = 0. 05.

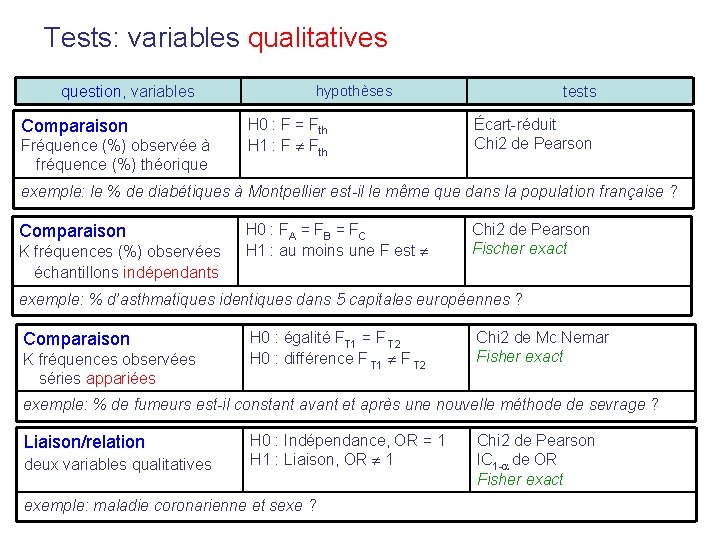
Tests: variables qualitatives question, variables Comparaison Fréquence (%) observée à fréquence (%) théorique hypothèses H 0 : F = Fth H 1 : F Fth tests Écart-réduit Chi 2 de Pearson exemple: le % de diabétiques à Montpellier est-il le même que dans la population française ? Comparaison K fréquences (%) observées échantillons indépendants H 0 : FA = FB = FC H 1 : au moins une F est Chi 2 de Pearson Fischer exact exemple: % d’asthmatiques identiques dans 5 capitales européennes ? Comparaison K fréquences observées séries appariées H 0 : égalité FT 1 = F T 2 H 0 : différence F T 1 F T 2 Chi 2 de Mc Nemar Fisher exact exemple: % de fumeurs est-il constant avant et après une nouvelle méthode de sevrage ? Liaison/relation deux variables qualitatives H 0 : Indépendance, OR = 1 H 1 : Liaison, OR 1 exemple: maladie coronarienne et sexe ? Chi 2 de Pearson IC 1 - de OR Fisher exact

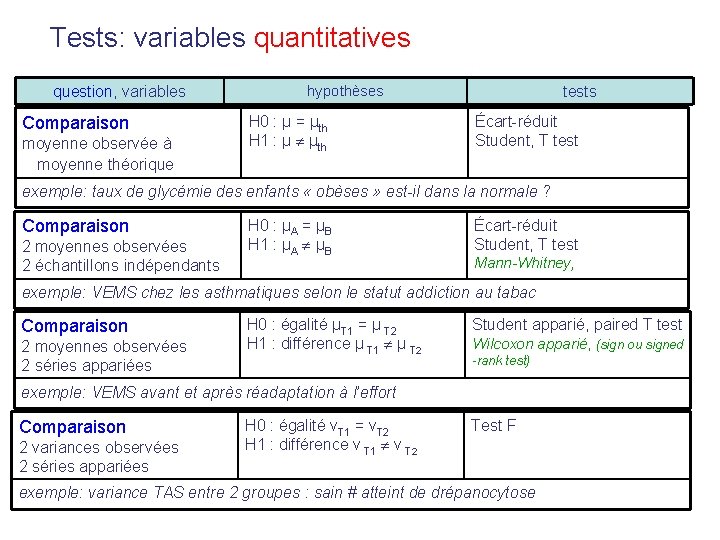
Tests: variables quantitatives question, variables Comparaison moyenne observée à moyenne théorique hypothèses H 0 : µ = µth H 1 : µ µth tests Écart-réduit Student, T test exemple: taux de glycémie des enfants « obèses » est-il dans la normale ? Comparaison 2 moyennes observées 2 échantillons indépendants H 0 : µA = µB H 1 : µA µB Écart-réduit Student, T test Mann-Whitney, exemple: VEMS chez les asthmatiques selon le statut addiction au tabac Comparaison 2 moyennes observées 2 séries appariées H 0 : égalité µT 1 = µ T 2 H 1 : différence µ T 1 µ T 2 Student apparié, paired T test Wilcoxon apparié, (sign ou signed -rank test) exemple: VEMS avant et après réadaptation à l’effort Comparaison 2 variances observées 2 séries appariées H 0 : égalité v. T 1 = v. T 2 H 1 : différence v T 1 v T 2 Test F exemple: variance TAS entre 2 groupes : sain # atteint de drépanocytose

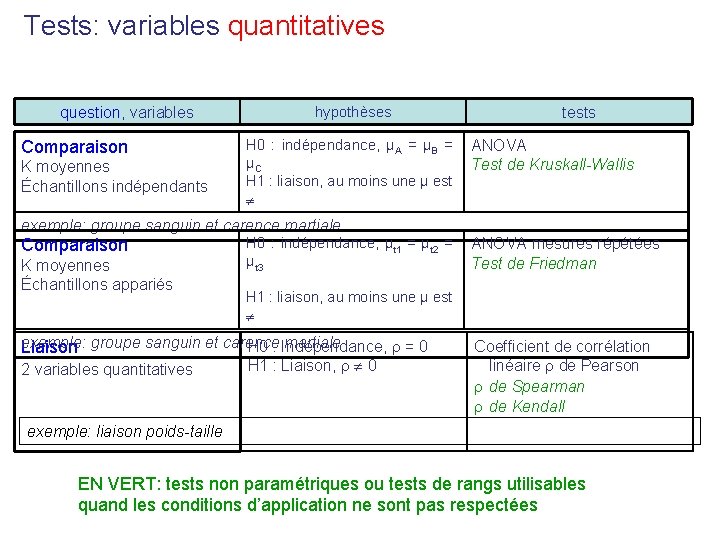
Tests: variables quantitatives question, variables Comparaison K moyennes Échantillons indépendants hypothèses tests H 0 : indépendance, µA = µB = ANOVA µC Test de Kruskall-Wallis H 1 : liaison, au moins une µ est exemple: groupe sanguin et carence martiale Comparaison K moyennes Échantillons appariés H 0 : indépendance, µt 1 = µt 2 = ANOVA mesures répétées µt 3 Test de Friedman H 1 : liaison, au moins une µ est exemple: groupe sanguin et carence martiale H 0 : Indépendance, = 0 Liaison H 1 : Liaison, 0 2 variables quantitatives Coefficient de corrélation linéaire de Pearson de Spearman de Kendall exemple: liaison poids-taille EN VERT: tests non paramétriques ou tests de rangs utilisables quand les conditions d’application ne sont pas respectées

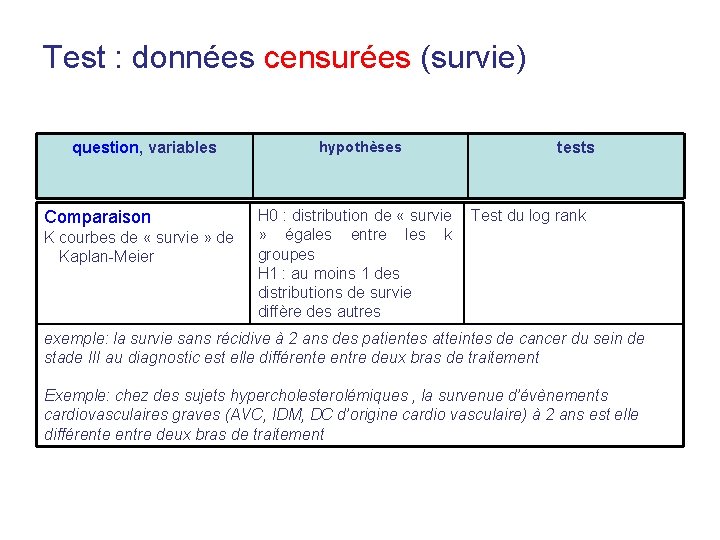
Test : données censurées (survie) question, variables Comparaison K courbes de « survie » de Kaplan-Meier hypothèses tests H 0 : distribution de « survie Test du log rank » égales entre les k groupes H 1 : au moins 1 des distributions de survie diffère des autres exemple: la survie sans récidive à 2 ans des patientes atteintes de cancer du sein de stade III au diagnostic est elle différente entre deux bras de traitement Exemple: chez des sujets hypercholesterolémiques , la survenue d’évènements cardiovasculaires graves (AVC, IDM, DC d’origine cardio vasculaire) à 2 ans est elle différente entre deux bras de traitement

Tests statistiques : Conclusion Les noms des tests sont variables selon les auteurs et les références. D’autres tests existent … Beaucoup d’autres tests… Le principe général reste le même ! Vers l’épidémiologie : Les tests statistiques permettent une conclusion statistique. Pour faire une conclusion clinique, il convient de prendre des précautions: recherche de biais, intérêt clinique… Causalité et association ne sont pas équivalentes !