La Statistique Descriptive Professeur TALEB Mahir mahir taleb

La Statistique Descriptive Professeur TALEB Mahir mahir, taleb 2020@gmail. com

Buts • Ensembles de méthodes dont le but est de présenter les données pour que l'on puisse en prendre connaissance facilement. • Cela peut concerner : – une variable à la fois : statistique à une dimension, – deux variables à la fois : statistique à deux dimensions, – plus de deux variables à la fois : statistique multidimensionnelle.

Statistique descriptive • Ces méthodes comportent : – Les tableaux : distributions de fréquences. – Les diagrammes : graphiques. – Les paramètres statistiques : • Réduction des données à quelques valeurs numériques caractéristiques.

Rappel • 3 Types de données : – Qualitatives (présence ou absence d’une caractéristique) • Binaires, • Nominales. – Quantitatives (compte ou mesure) • Discontinues, • Continues. – Ordinales (rang)

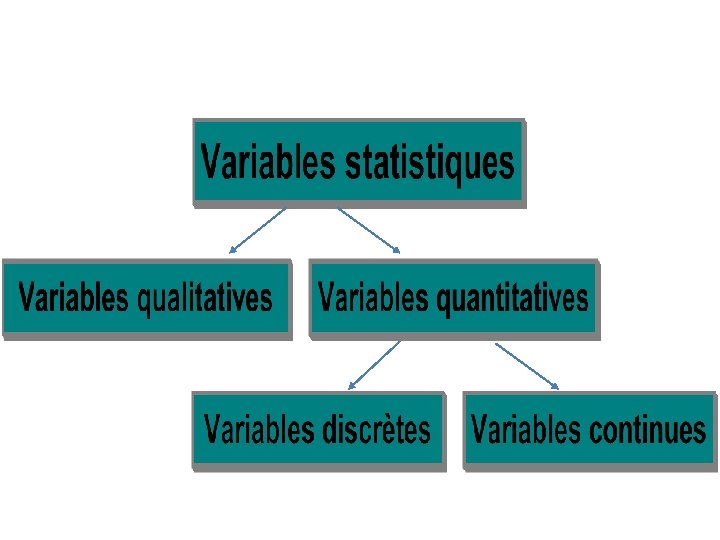
Distributions de fréquences • Concernent les 3 types de données avec des points communs et des points spécifiques à chacun des types. • Séries statistiques (tout type de données) : – Enumération des résultats : • Exemples : – Couleurs des cheveux : blond, brun, blond, noir…. – Nombre d’enfants dans les familles : 1, 2, 1, 4, 0 …. – Séries statistiques ordonnées : • Ne concernent que les données quantitatives et ordinales • Enumération du plus petit au plus grand – Exemple : Nombre d’enfants : 0, 1, 1, 2, 4 …. • Le nombre total d’observations est l’effectif. Il est noté n (certain le note N).

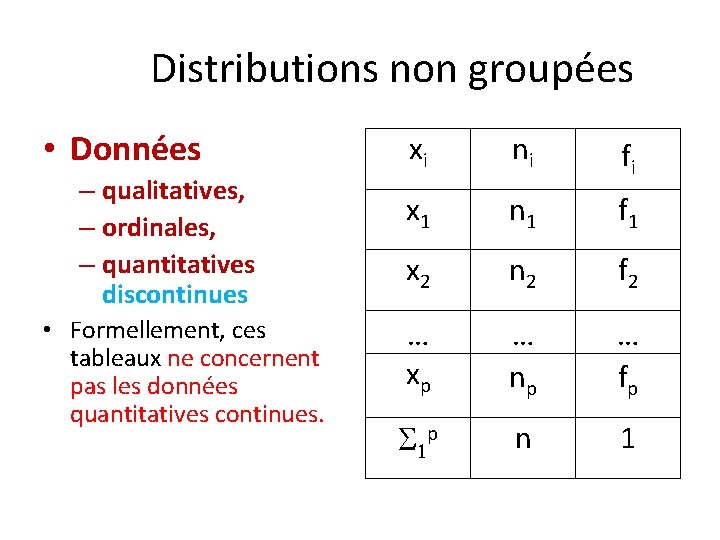
Distributions non groupées • Données – qualitatives, – ordinales, – quantitatives discontinues • Formellement, ces tableaux ne concernent pas les données quantitatives continues. xi ni fi x 1 n 1 f 1 x 2 n 2 f 2 … xp … np … fp S 1 p n 1

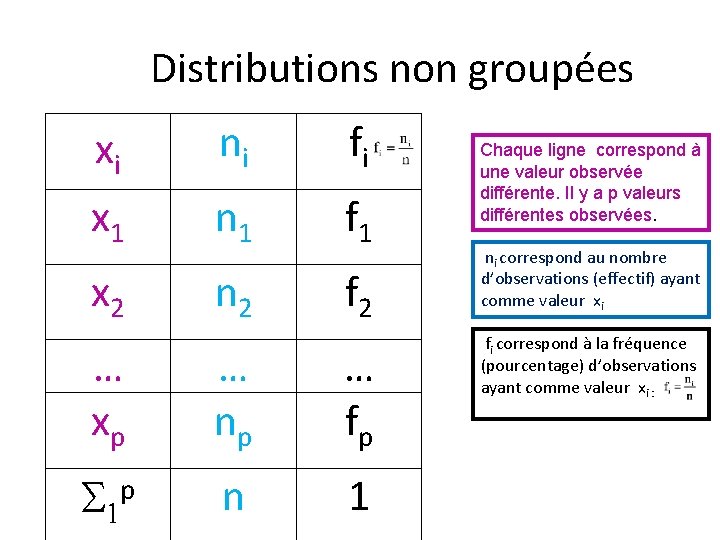
Distributions non groupées xi ni fi x 1 n 1 f 1 x 2 n 2 f 2 … xp … np … fp p S 1 n 1 Chaque ligne correspond à une valeur observée différente. Il y a p valeurs différentes observées. ni correspond au nombre d’observations (effectif) ayant comme valeur xi fi correspond à la fréquence (pourcentage) d’observations ayant comme valeur xi :

Notations sur les séries statistiques {. . . } = collection d'éléments {xi}1≤i≤n est un raccourci pour {x 1, x 2, . . . , xi, . . . , xn} Je le noterai parfois simplement {xi}n ou {xi} Les notations où interviennent des majuscules se réfèrent à des recensements (directement sur toute la population). Ainsi : {Xi}N

Distributions non groupées • Données ordinales et quantitatives discontinues. • x 1 est la plus petite valeur, xp la plus grande des valeurs observées. • Effectifs cumulés. – N 2 = n 2+n 1 • Fréquences cumulées. – F 2 = f 2+f 1 xi ni fi Ni Fi x 1 n 1 f 1 N 1 F 1 x 2 n 2 f 2 N 2 F 2 … … xp n p … …. … fp N p F p S 1 p n 1

Distributions non groupées xi ni fi Ni Fi x 1 n 1 f 1 N 1 F 1 x 2 n 2 f 2 N 2 F 2 … … xp n p … …. … fp N p F p S 1 p n 1 Ni est l’effectif cumulé c’est dire le nombre d’observations ayant des valeurs inférieures ou égales à xi : Fi est la fréquence cumulée c’est à dire la fréquence des observations ayant des valeurs inférieures ou égales à xi :

Distributions groupées • Les valeurs sont mises en classes. • Toutes les distributions relatives à des variables continues doivent être considérées comme des distributions groupées, puisque l'infinité de valeurs admissibles est condensée en un nombre fini de mesures en fonction de la précision de la méthode de mesure utilisée.

A propos des classes • Leurs valeurs extrêmes sont appelées bornes des classes. • Les classes sont mutuellement exclusives. • L'amplitude de la classe ou intervalle ou module de classe : D= borne supérieure - la borne inférieure. • Le point central ou encore point médian est situé à mi chemin entre les bornes. – Ci = Binfi +Di/2 • Dans certains cas la limite inférieure de la première classe ou supérieure de la dernière classe n'est pas précisée. On parle de classes ouvertes. A éviter !. . .

A propos des classes • L'intervalle de classe est généralement constant, toutefois, on utilise parfois une amplitude variable notamment pour les classes des valeurs extrêmes. • En cas de classes d'amplitudes différentes, la densité de fréquence ni/ Di permet de comparer les effectifs ou les fréquences d'une classe à l'autre. • la densité de fréquence est utilisée pour tracer l’histogramme.

Données quantitatives continues • Remarques : – Si l’on mesure le poids d’un nouveau né avec une précision de 1 g, l’enfant qui pèse 3500 g a en fait un poids compris entre [3499, 5 g et 3500, 5 g[. 3500 g représente le centre de la classe. – Si l’on mesure l’âge en années pleines des individus, une personne de 20 ans a un âge compris entre [20 ans (inclus) et 21 ans[ (exclu). 20 ans représente la borne inférieure de la classe.

Distribution groupée • On remplace la colonne xi par une colonne qui comprend soit les bornes de classes, soit le centre de classe ou la borne inférieure de la classe (données temporelles comme l’âge en années pleines).

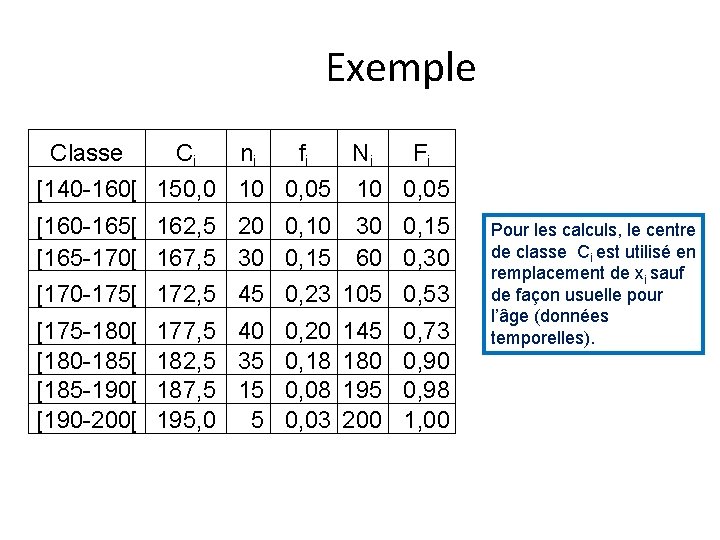
Exemple Classe Ci ni fi Ni F i [140 -160[ 150, 0 10 0, 05 [160 -165[ 162, 5 20 0, 10 30 0, 15 [165 -170[ 167, 5 30 0, 15 60 0, 30 [170 -175[ 172, 5 45 0, 23 105 0, 53 [175 -180[ [180 -185[ [185 -190[ [190 -200[ 177, 5 40 0, 20 145 0, 73 182, 5 35 0, 18 180 0, 90 187, 5 15 0, 08 195 0, 98 195, 0 5 0, 03 200 1, 00 Pour les calculs, le centre de classe Ci est utilisé en remplacement de xi sauf de façon usuelle pour l’âge (données temporelles).

Formules p = nombre de valeurs différentes observées

En pratique • Pour les calculs des paramètres statistiques usuels des données quantitatives et uniquement de ce type de données. • On complète la distribution par : – Une colonne ni * xi pour calculer le total, – Une colonne ni * xi 2 pour calculer le total des carrés.

Les graphiques représentent les distributions • Distributions non cumulées – Distributions non groupées • Données qualitatives : – Diagramme sectoriel § Angle au centre proportionnel à ni (ou fi). • Données quantitatives discrètes – Diagramme en bâtons § On trace parallèlement à l'axe des ordonnées, en regard des xi qui sont portés en abscisse, un segment de longueur proportionnel à ni – Polygone des fréquences § Ligne brisée joignant les bâtons. § Fréquences absolues / fréquences relatives.

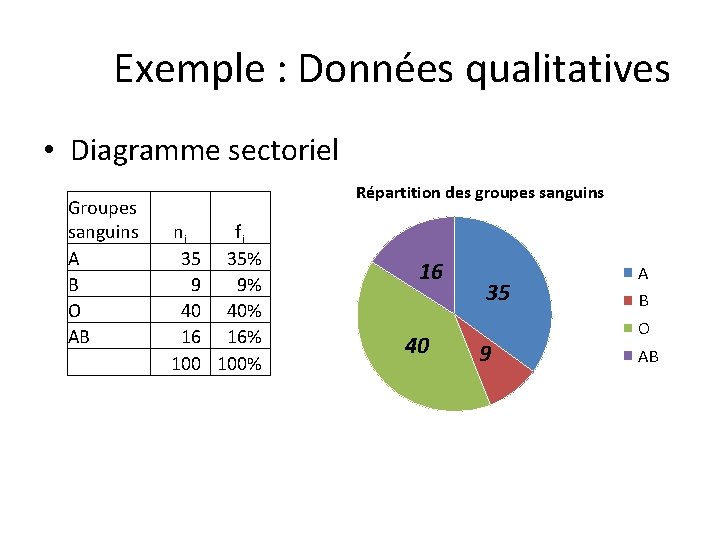
Exemple : Données qualitatives • Diagramme sectoriel Groupes sanguins A B O AB Répartition des groupes sanguins ni fi 35 35% 9 9% 40 40% 16 16% 100% 16 40 35 9 A B O AB

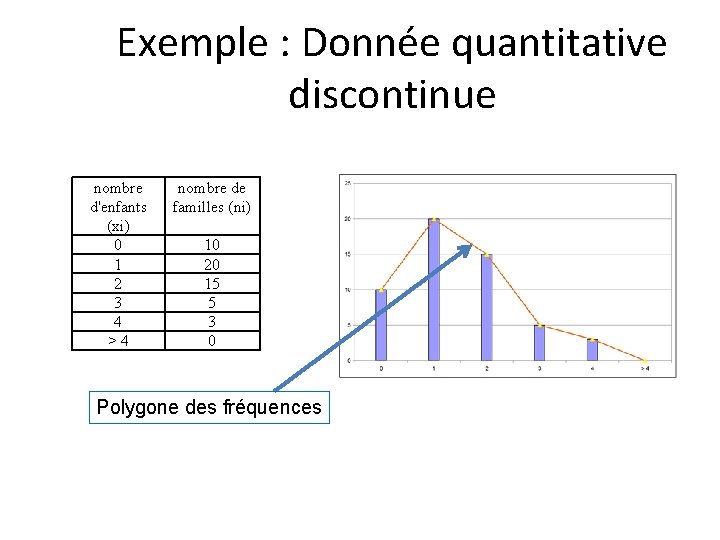
Exemple : Donnée quantitative discontinue nombre d'enfants (xi) 0 1 2 3 4 >4 nombre de familles (ni) 10 20 15 5 3 0 Polygone des fréquences

Les graphiques représentent les distributions • Distributions non cumulées – Distributions groupées • Données quantitatives – Histogramme : § Composé de rectangles ayant comme base l'intervalle de classe et comme hauteur la densité de fréquence (ni/Di). § La surface est proportionnelle à ni.

Les graphiques représentent les distributions • Distributions cumulées – Uniquement pour des données quantitatives • Polygone des fréquences : – Distributions non groupées = escalier. – Distributions groupées = ligne brisée. • Histogrammes.

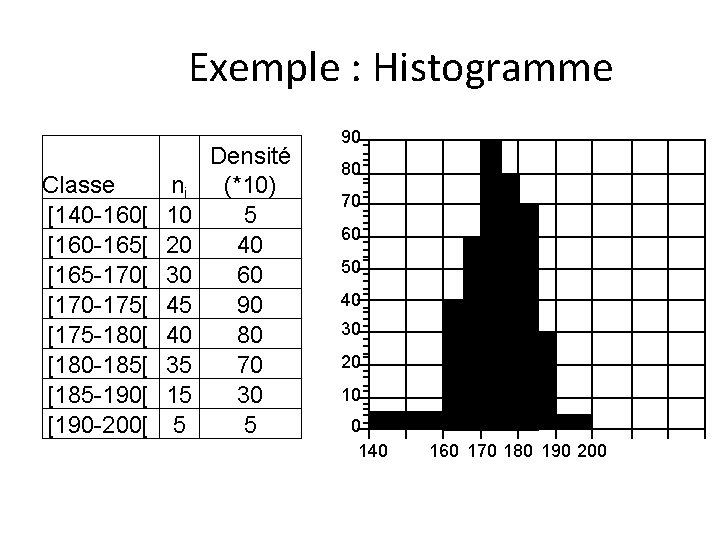
Exemple : Histogramme Classe [140 -160[ [160 -165[ [165 -170[ [170 -175[ [175 -180[ [180 -185[ [185 -190[ [190 -200[ n i 10 20 30 45 40 35 15 5 Densité (*10) 5 40 60 90 80 70 30 5 90 80 70 60 50 40 30 20 10 0 140 160 170 180 190 200

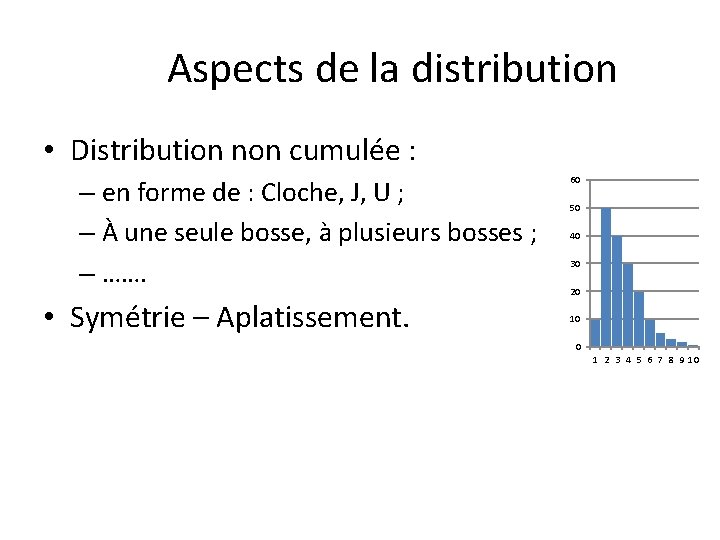
Aspects de la distribution • Distribution non cumulée : – en forme de : Cloche, J, U ; – À une seule bosse, à plusieurs bosses ; – ……. • Symétrie – Aplatissement. 60 50 40 30 20 10 0 1 2 3 4 5 6 7 8 9 10

Remarques • Autres représentations : – Diagramme de Pareto et courbe ABC ; – Boite à moustache (Box-plot). • Attention : – Les tableurs comme Excel ou Calc ne permettent pas facilement de faire des histogrammes.

Diagramme de Pareto • Dans le domaine de la qualité, on étudie les causes de dysfonctionnement d'un système. • Quand il s'agit de variables qualitatives binaires, on présente les résultats sous forme de diagramme de Pareto et de courbe ABC. • Objectif : Visualiser les causes les plus fréquentes de défaut de qualité.

Exemple • La tenue des dossiers médicaux fait l'objet de textes règlementaires contraignants. • l'évaluation de la qualité des dossiers fait partie du processus de certification. • Un dossiers peut avoir plusieurs anomalies. • On a étudié les anomalies rencontrées sur 200 dossiers.

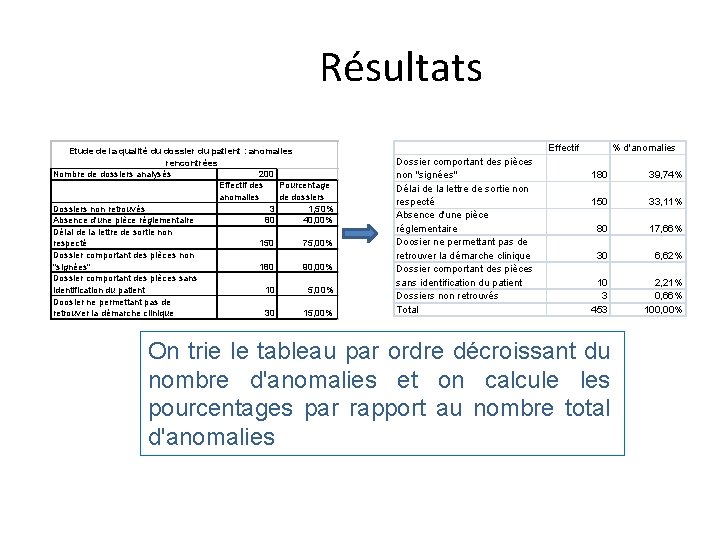
Résultats Etude de la qualité du dossier du patient : anomalies rencontrées Nombre de dossiers analysés 200 Effectif des Pourcentage anomalies de dossiers Dossiers non retrouvés 3 1, 50% Absence d'une pièce réglementaire 80 40, 00% Délai de la lettre de sortie non respecté 150 75, 00% Dossier comportant des pièces non "signées" 180 90, 00% Dossier comportant des pièces sans identification du patient 10 5, 00% Doosier ne permettant pas de retrouver la démarche clinique 30 15, 00% Effectif Dossier comportant des pièces non "signées" Délai de la lettre de sortie non respecté Absence d'une pièce réglementaire Doosier ne permettant pas de retrouver la démarche clinique Dossier comportant des pièces sans identification du patient Dossiers non retrouvés Total % d'anomalies 180 39, 74% 150 33, 11% 80 17, 66% 30 6, 62% 10 3 453 2, 21% 0, 66% 100, 00% On trie le tableau par ordre décroissant du nombre d'anomalies et on calcule les pourcentages par rapport au nombre total d'anomalies

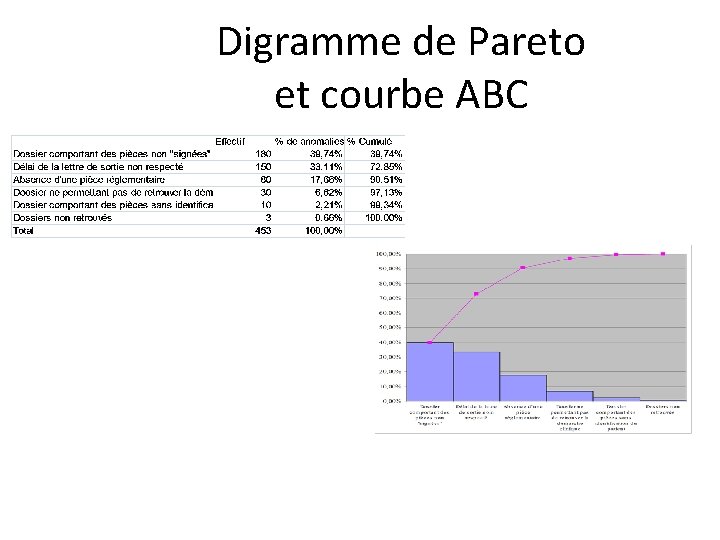
Digramme de Pareto et courbe ABC

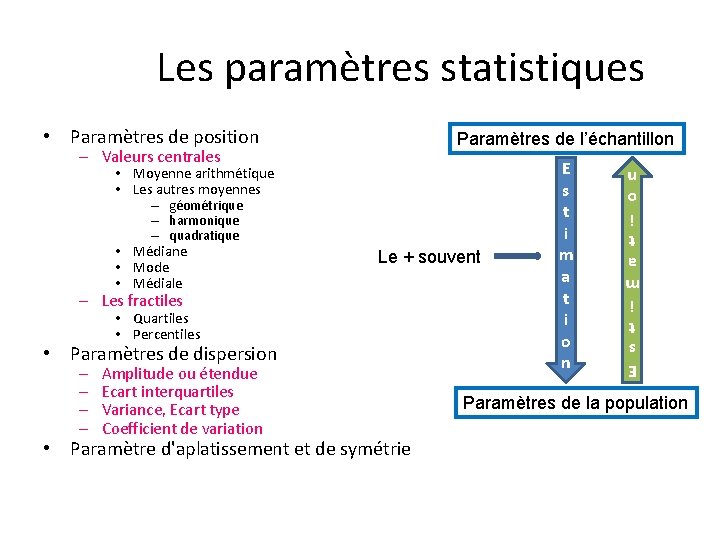
Les paramètres statistiques • Paramètres de position Paramètres de l’échantillon • Moyenne arithmétique • Les autres moyennes – géométrique – harmonique – quadratique • Médiane • Mode • Médiale Le + souvent – Les fractiles • Quartiles • Percentiles • Paramètres de dispersion – – Amplitude ou étendue Ecart interquartiles Variance, Ecart type Coefficient de variation • Paramètre d'aplatissement et de symétrie E s t i m a t i o n – Valeurs centrales Paramètres de la population

Moyenne Arithmétique Population m (mean) Echantillon x (average) • Appelée moyenne notée – Paramètre central qui concerne bien évidemment uniquement des variables quantitatives. – Dans l’unité de la variable. – Calculable quelque soit la loi qui régit la distribution. – Somme des valeurs (T) divisée par le nombre de mesures (n). – Suivant la forme de présentation des observations, différentes formules de calcul peuvent être employées.

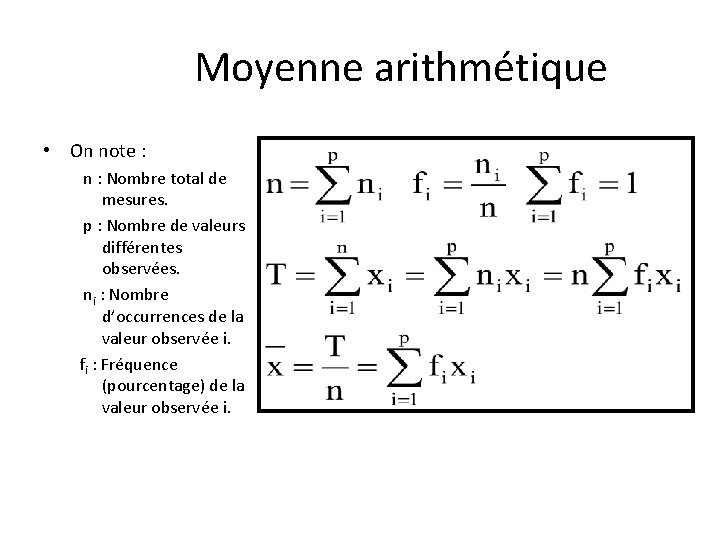
Moyenne arithmétique • On note : n : Nombre total de mesures. p : Nombre de valeurs différentes observées. ni : Nombre d’occurrences de la valeur observée i. fi : Fréquence (pourcentage) de la valeur observée i.

Moyenne arithmétique • Propriétés : – Centre de gravité de la distribution. – La somme des écarts à la moyenne est nulle. – Affectée par les changements de variable. • Si y = ax + b; on a : y = ax + b – La moyenne contrairement à la médiane est très sensible aux valeurs extrêmes. – La moyenne d'un groupe résultant de la fusion d'autres groupes n'est égale à la moyenne des moyennes que si tous les groupes ont le même effectif. – Dans une distribution en cloche, unimodale et symétrique, moyenne, mode et médiane sont confondus.

Distribution des moyennes de plusieurs échantillons • La moyenne de l'échantillon est le meilleur estimateur de la moyenne de la population. • La distribution des moyennes de petits échantillons (n<30) indépendants tirés de la même population suit une loi normale si la distribution de la variable est normale. • Au-delà de 30, la distribution des moyennes suit une loi normale sans condition sur la distribution de la variable.

Exemple • Soit la série correspondant aux tailles en cm de 6 étudiants : 160, 170, 180, 190, 200. n = 6; T = 160+170+180+190+200 = 1080

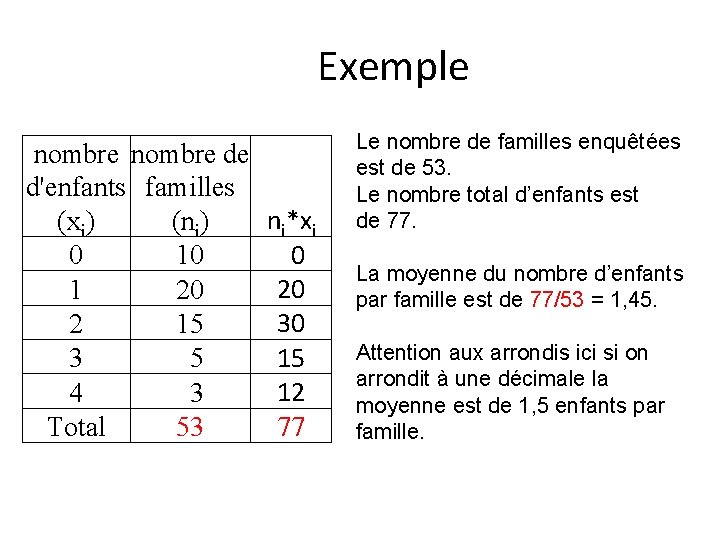
Exemple nombre de d'enfants familles (xi) (ni) 0 10 1 20 2 15 3 5 4 3 Total 53 ni*xi 0 20 30 15 12 77 Le nombre de familles enquêtées est de 53. Le nombre total d’enfants est de 77. La moyenne du nombre d’enfants par famille est de 77/53 = 1, 45. Attention aux arrondis ici si on arrondit à une décimale la moyenne est de 1, 5 enfants par famille.

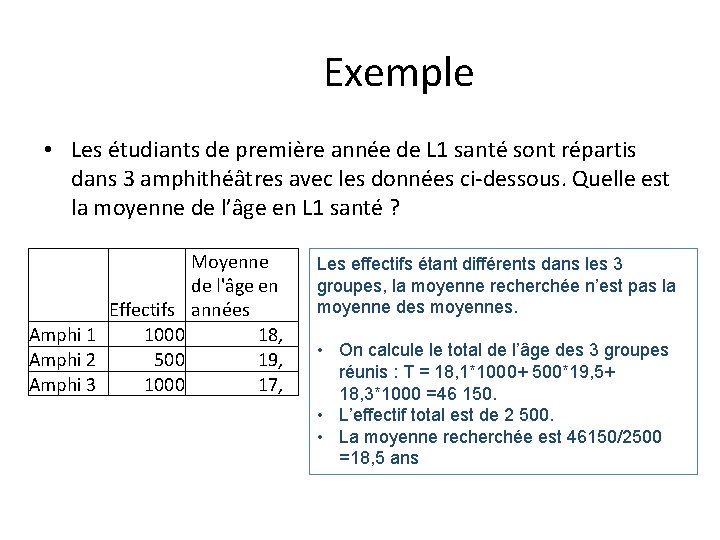
Exemple • Les étudiants de première année de L 1 santé sont répartis dans 3 amphithéâtres avec les données ci-dessous. Quelle est la moyenne de l’âge en L 1 santé ? Effectifs Amphi 1 1000 Amphi 2 500 Amphi 3 1000 Moyenne de l'âge en années 18, 19, 17, Les effectifs étant différents dans les 3 groupes, la moyenne recherchée n’est pas la moyenne des moyennes. • On calcule le total de l’âge des 3 groupes réunis : T = 18, 1*1000+ 500*19, 5+ 18, 3*1000 =46 150. • L’effectif total est de 2 500. • La moyenne recherchée est 46150/2500 =18, 5 ans

Les autres moyennes • Moyenne géométrique d'une série de valeurs positives est la racine nième du produit des n valeurs. Elle est toujours inférieure ou égale à la moyenne arithmétique. • Moyenne harmonique d'une série de valeurs positives est égale à l'inverse de la moyenne des inverses. • Moyenne quadratique est la racine carré de la moyenne arithmétique des carrés.

La médiane • La médiane notée x (tilde) est telle que la moitié des observations lui sont inférieure (ou égale) et la moitié supérieure (ou égale) : xi tel que Fi = 0, 5. – Sur les distributions symétriques unimodales en cloche (normales par exemple) la médiane est égale à la moyenne et au mode. – Paramètre peu sensible aux valeurs extrêmes. – Peut être utilisée pour des données ordinales.

La médiane : calcul • Sur une distribution non groupée : – Si n impair, la médiane est l'observation de rang (N+1)/2 – Si n est pair, tout nombre entre x. N/2 et x. N/2+1 convient. On prend la moyenne (pondérée en cas d'ex-aequo) entre ces deux valeurs. • Sur une distribution groupée, la classe médiane est celle qui contient la médiane. – Détermination graphique. – En admettant que les observations soient réparties uniformément dans cette classe, on réalise une approximation linéaire.

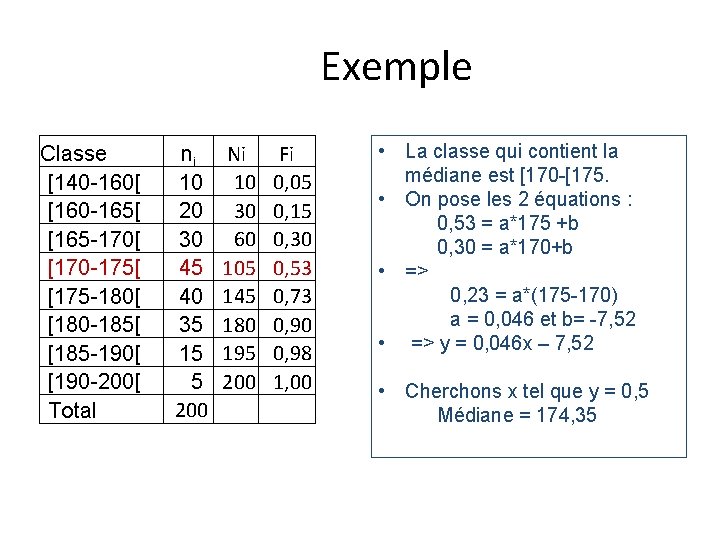
Exemple Classe [140 -160[ [160 -165[ [165 -170[ [170 -175[ [175 -180[ [180 -185[ [185 -190[ [190 -200[ Total n i 10 20 30 45 40 35 15 5 200 Ni 10 30 60 105 145 180 195 200 Fi 0, 05 0, 15 0, 30 0, 53 0, 73 0, 90 0, 98 1, 00 • La classe qui contient la médiane est [170 -[175. • On pose les 2 équations : 0, 53 = a*175 +b 0, 30 = a*170+b • => 0, 23 = a*(175 -170) a = 0, 046 et b= -7, 52 • => y = 0, 046 x – 7, 52 • Cherchons x tel que y = 0, 5 Médiane = 174, 35

Mode • Mode encore appelé valeur dominante : – Correspond à la valeur la plus fréquente. xi correspondant au ni (ou fi)maximum. – Il peut y avoir un ou plusieurs modes. • Rappel : – Dans les distributions en cloche, unimodales symétriques, mode, médiane et moyenne sont confondus.

Fractiles • Quartiles – Q 1: xi tel que Fi = 0, 25 => 1/4 des valeurs lui sont inférieures, 3/4 lui sont supérieures. – Q 2 = Médiane. – Q 3 : xi tel que Fi = 0, 75 => 3/4 des valeurs lui sont inférieures, 1/4 lui sont supérieures. • Détermination graphique. • Interpolation linéaire (cf médiane). • Percentiles – 10 ième percentile : xi tel que Fi = 0, 10

Remarques • On a : – 50% des individus qui ont des valeurs en dehors de l’intervalle Q 1 -Q 3 et 50% à l’intérieur. – 25% des individus qui ont des valeurs comprises entre Q 1 et médiane. – 25% des individus qui ont des valeurs comprises entre médiane et Q 3. – 25% des individus qui ont des valeurs inférieure à Q 1 – 25% des individus qui ont des valeurs supérieures à Q 3 – Ceci permet rapidement de se rendre compte si la distribution est symétrique ou non.

Paramètres de dispersion • • Amplitude ou étendue. Ecart interquartiles. Variance et écart type. Coefficient de variation.

Amplitude ou étendue • Ecart entre la valeur de l'observation maximale et celle de l'observation minimale. • Non définie pour les distributions groupées (tolérance pour les variables quantitatives continues de la précision de la mesure). • On montre que l'écart type est toujours inférieur ou égal à la moitié de l'amplitude. • Dans les distributions unimodales en cloche l'écart type est égal : – – au tiers de l'amplitude pour n de l'ordre de 10, au quart de l'amplitude pour n entre 15 et 50, au cinquième pour des effectifs de 50 à 200, au sixième pour des effectifs de 200 à 1000.

Ecart interquartiles (EIQ) • EIQ = Q 3 -Q 1. • Englobe 50% des observations. • On utilise parfois l'écart semi-interquartile (Q 3 -Q 1)/2.

Variance et écart type • La variance (variance) d'une série ou d'une distribution de fréquences est la moyenne arithmétique des carrés des écarts à la moyenne • C'est par rapport à la moyenne que la somme des carrés des écarts est la plus faible. • La variance de l'échantillon est souvent notée S 2. • Ce n'est pas un bon estimateur de la variance de la population souvent notée s 2. ^ 2. • L’estimation de la variance est notée s

Variance et écart type • Le numérateur de la variance est appelé somme des carrés des écarts et noté SCE. • L'écart type est la racine carré de la variance. On l'appelle également déviation standard (standard deviation). Il est dans l'unité de la variable. • Variance et écart type sont indépendants des translations (changement d ’origine) mais pas des multiplications (changement d'unité). – Si y = a * x + b, on a Sy = |a| * Sx • Pour les distributions en cloche, la variance calculée à partir des classes est surestimée, certain réalise la correction de Sheppard.

Formules

Ecart type de la moyenne • Si l’on considère plusieurs échantillons indépendants, issus d’une population, on obtient plusieurs moyennes. • La distribution des moyennes a un écart type appelé écart type de la moyenne ou erreur standard de la moyenne (ESM) (standard deviation of the mean – SDM).

Représentation en Box Plot • Résume la distribution en terme de paramètres de position et de dispersion.

Coefficient de variation • CV est le rapport écart type divisé par la moyenne. • CV est un nombre pur, sans unités. • CV est totalement indépendant des unités. • Le CV permet de comparer la variabilité de distributions de variables qui ne sont pas dans les mêmes unités.

Moments centrés d’ordre k. Symétrie et aplatissement • Moments centrés d'ordre k – moyenne arithmétique des écarts à la moyenne élevée à la puissance k. – si k pair => paramètre de dispersion. – si k impair => paramètre de symétrie. • Coefficient de Pearson et de Fisher – b 1 pour caractériser la symétrie de la courbe; b 2 pour caractériser l'aplatissement. – b 1 = M 32 / M 23 : est voisin de 0 si la distribution est symétrique. – b 2 = M 4 / M 22 : est voisin de 3 si la distribution suit une loi normale (plus aplatie qu'elle si b 2 < 3). – cf Loi Normale.

Statistique descriptive à 2 dimensions • Objectif : mettre en évidence les relations qui existent entre deux séries d'observations. – Nature des variables : les deux variables peuvent être quantitatives, qualitatives ou l'une quantitative et l'autre qualitative. – Deux variables mesurées chez le même individu par exemple poids et taille; poids et couleur des yeux, présence d’un cancer et éthylisme. . . • Situations : – Séries appariées : même variable mesurée dans deux circonstances : • Avant - Après traitement. • Cas - Témoins on apparie un témoin dépourvu de la maladie que l'on veut étudier sur différents points que l'on sait lier au phénomène étudié (par exemple pour une étude de la mortalité on apparie sur âge, sexe, . . . – Séries non appariées : • Même variable mesurée dans des groupes différents.

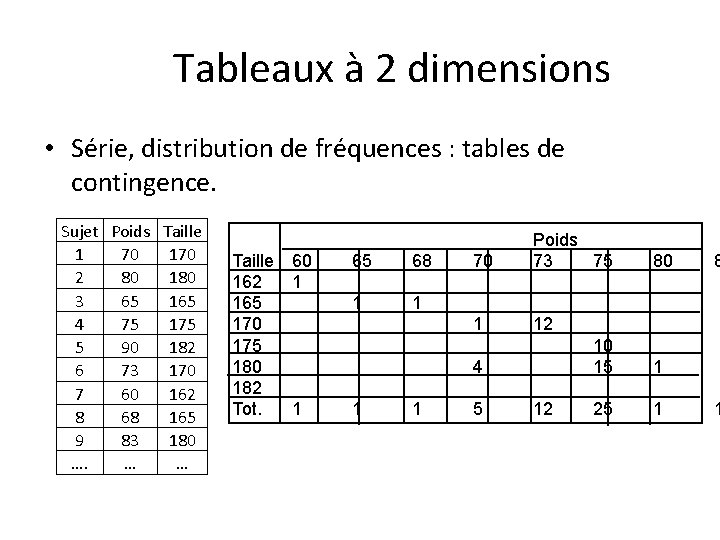
Tableaux à 2 dimensions • Série, distribution de fréquences : tables de contingence. Sujet Poids Taille 1 70 170 2 80 180 3 65 165 4 75 175 5 90 182 6 73 170 7 60 162 8 68 165 9 83 180 …. … … Taille 60 162 1 165 170 175 180 182 Tot. 1 65 68 1 1 70 Poids 73 75 1 12 4 1 1 5 12 80 10 15 1 25 1 8 1

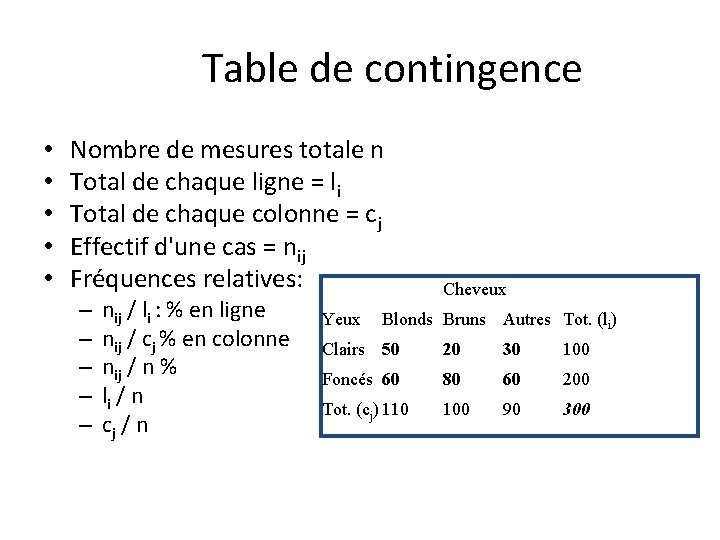
Table de contingence • • • Nombre de mesures totale n Total de chaque ligne = li Total de chaque colonne = cj Effectif d'une cas = nij Fréquences relatives: – – – nij / li : % en ligne nij / cj % en colonne nij / n % li / n cj / n Yeux Cheveux Blonds Bruns Autres Tot. (li) Clairs 50 20 30 100 Foncés 60 80 60 200 Tot. (cj) 110 100 90 300

Attention Cheveux Yeux 300 = Nombre total de mesures. Blonds Bruns Autres Tot. (li) Clairs 50 20 30 100 Foncés 60 80 60 200 Tot. (cj) 110 100 90 300 100 = Nombre d'individus ayant les yeux clairs. 110 = Nombre d'individus ayant les cheveux blonds. 50 / 300 = % d'individus ayant les cheveux blonds et les yeux clairs. 50 / 110 = % d'individus parmi les blonds ayant les yeux clairs. 50 / 100 = % d'individus parmi les yeux clairs ayant les cheveux blonds.

Représentation graphique 2 variables quantitatives • Nuage de points 90 85 80 75 70 65 60 55 160 165 170 175 180 185

Covariance •

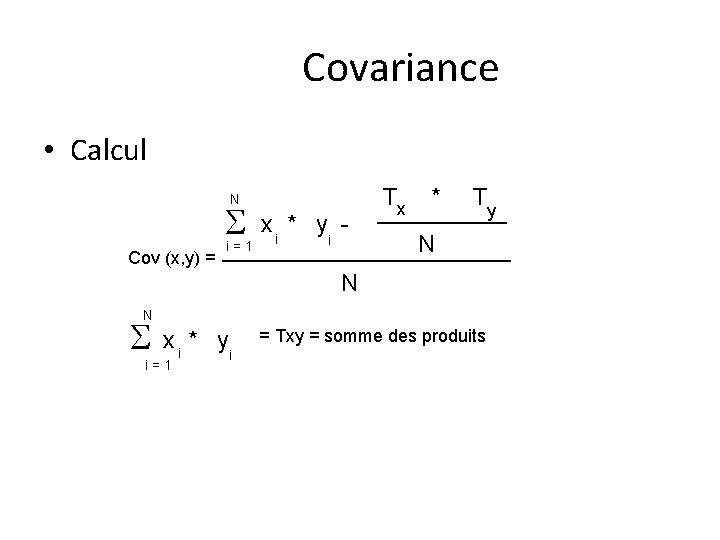
Covariance • Calcul N S Cov (x, y) = i = 1 x * y i i T * T x y N N N S x * y i i = 1 i = Txy = somme des produits

Table de contingence de 2 caractères binaires • Très utilisées en santé : – Recherche de facteur de risque : exemple enquêtes exposés/non exposés. – Evaluation d’un test diagnostic.

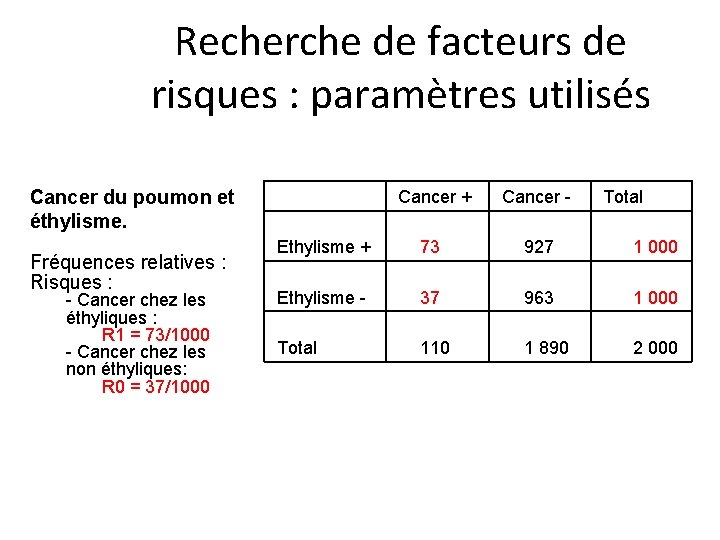
Recherche de facteurs de risques : paramètres utilisés Cancer du poumon et éthylisme. Fréquences relatives : Risques : - Cancer chez les éthyliques : R 1 = 73/1000 - Cancer chez les non éthyliques: R 0 = 37/1000 Cancer + Cancer - Total Ethylisme + 73 927 1 000 Ethylisme - 37 963 1 000 Total 110 1 890 2 000

Risque relatif et odds ratio • RR est le rapport du risque chez les exposés (R 1) sur le risque des non exposés (R 0). – RR = R 1/R 0 = 0, 073/0, 037 =1, 97 • Cote (Odds) (cf course de chevaux). – Chez les éthyliques R 1/(1 -R 1) = 0, 79 – Chez les non éthyliques R 0/(1 -R 0) = 0, 038 • Odds ratio (OR) ou rapport de cotes. – OR = 0, 79/0, 038 = 2, 05 • L’OR est souvent utilisé en épidémiologie. Si la fréquence de la maladie est faible, les valeurs de OR et de RR sont très proches.

Recherche de facteurs de confusion • On a montré que l’on avait 1, 97 fois plus de chance de faire un cancer du poumon si l’on boit que si l’on ne boit pas… Mais ? • Un facteur de confusion est simultanément facteur de risque pour la maladie et est une variable associée à l'exposition. – Les facteurs de confusion potentiels sont le tabagisme et le sexe. • La première variable à considérer est le « tabagisme » .

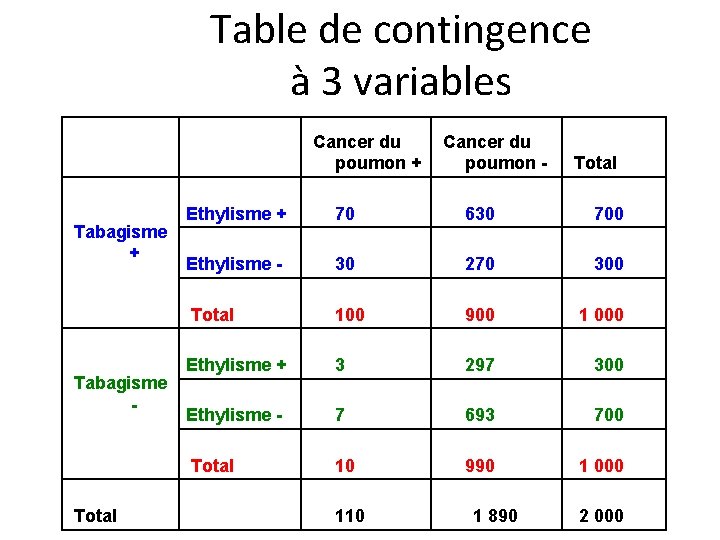
Table de contingence à 3 variables Cancer du poumon + poumon - Total Ethylisme + 70 630 700 Tabagisme + Ethylisme - Total 30 270 300 100 900 1 000 Ethylisme + 3 297 300 Tabagisme - Ethylisme - Total 7 693 700 Total 10 990 1 000 110 1 890 2 000

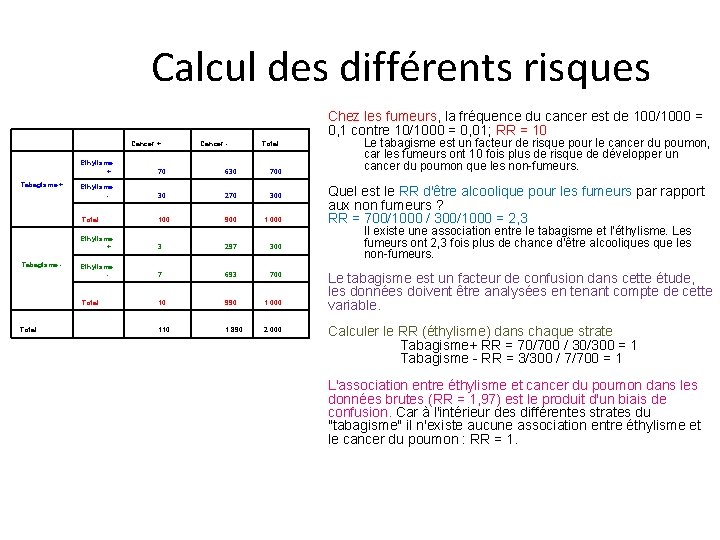
Calcul des différents risques Chez les fumeurs, la fréquence du cancer est de 100/1000 = 0, 1 contre 10/1000 = 0, 01; RR = 10 Tabagisme + Tabagisme - Total Cancer + Cancer - Total Ethylisme + 70 630 700 Ethylisme - 30 270 300 Total 100 900 1 000 Ethylisme + 3 297 300 Ethylisme - 7 693 700 Total 10 990 1 000 110 1 890 2 000 Le tabagisme est un facteur de risque pour le cancer du poumon, car les fumeurs ont 10 fois plus de risque de développer un cancer du poumon que les non-fumeurs. Quel est le RR d'être alcoolique pour les fumeurs par rapport aux non fumeurs ? RR = 700/1000 / 300/1000 = 2, 3 Il existe une association entre le tabagisme et l'éthylisme. Les fumeurs ont 2, 3 fois plus de chance d'être alcooliques que les non-fumeurs. Le tabagisme est un facteur de confusion dans cette étude, les données doivent être analysées en tenant compte de cette variable. Calculer le RR (éthylisme) dans chaque strate Tabagisme+ RR = 70/700 / 30/300 = 1 Tabagisme - RR = 3/300 / 7/700 = 1 L'association entre éthylisme et cancer du poumon dans les données brutes (RR = 1, 97) est le produit d'un biais de confusion. Car à l'intérieur des différentes strates du "tabagisme" il n'existe aucune association entre éthylisme et le cancer du poumon : RR = 1.

Quelques indicateurs utilisés en statistiques hospitalières Lits. Entrées et Sorties. Durée moyenne de séjour : DMS. Coefficient (taux d’occupation) des lits, Lits occupés. • Effectifs et équivalents temps pleins. • •

Lits • Comment compter les lits dans un hôpital ? – Lits Installés au 1 er janvier. – Lits disponibles pendant un période : • Comment comptabiliser l’indisponibilité ? – – Fermeture pour désinfection, Fermeture par manque d’effectifs soignants, Fermeture par manque de malades, …. .

Entrées, sorties, malades présents • On parle d’entrées ou de sorties pendant une période donnée. Date de début 2 4 3 1 1 Date de fin 10 4 4 3 30 4 Chaque trait représente un malade. - 3 entrées - 4 sorties - 6 présents Et pour les journées ? - 21 j (entrants) - 23 J (sortants) - 52 J (présents)

Durée moyenne de séjours : • Durée de séjour PMSI = DS-DE + 1 si décès. • DMS :

Taux d’occupation des lits et lits occupés

Effectifs, Equivalents temps plein • Les effectifs correspondent au nombre de personnes employées par la structure. • Les équivalents temps plein (ETP) représentent la force de travail. Une personne travaillant à temps partiel est comptabilisée en fonction de son temps de travail. • Par exemple un hospitalo-universitaire compte pour 0, 5 ETP.

Ph. D TALEB Mahir