Programa do Curso 1 O portal Genes Viso

Programa do Curso 1. O portal Genes – Visão Geral 1. Histórico 2. Caracterização 3. Aplicações 2. Inteligência Computacional 1. Redes Neurais 2. Lógica Fuzzy 3. Mapa de Kohonen

REDES NEURAIS Considerações Iniciais Inteligência Computacional Área da ciência que estuda a teoria e a aplicação de técnicas inspiradas na Natureza, como Redes Neurais, Lógica Nebulosa e Computação Evolucionária. Redes Neurais são modelos computacionais não lineares, inspirados na estrutura e operação do cérebro humano, que procuram reproduzir características humanas, tais como: aprendizado, associação, generalização e abstração. Devido à sua estrutura, as Redes Neurais são bastante efetivas no aprendizado de padrões a partir de dados não-linares, incompletos, com ruído e até compostos de exemplos contraditórios.

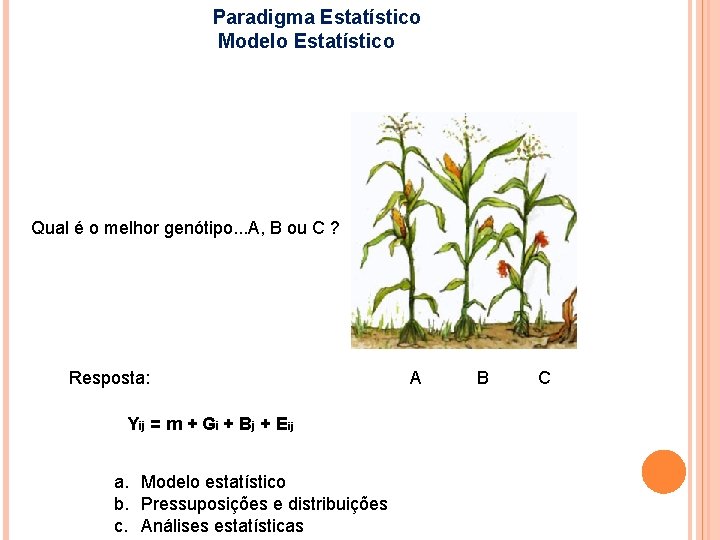
Paradigma Estatístico Modelo Estatístico Qual é o melhor genótipo. . . A, B ou C ? Resposta: Yij = m + Gi + Bj + Eij a. Modelo estatístico b. Pressuposições e distribuições c. Análises estatísticas A B C

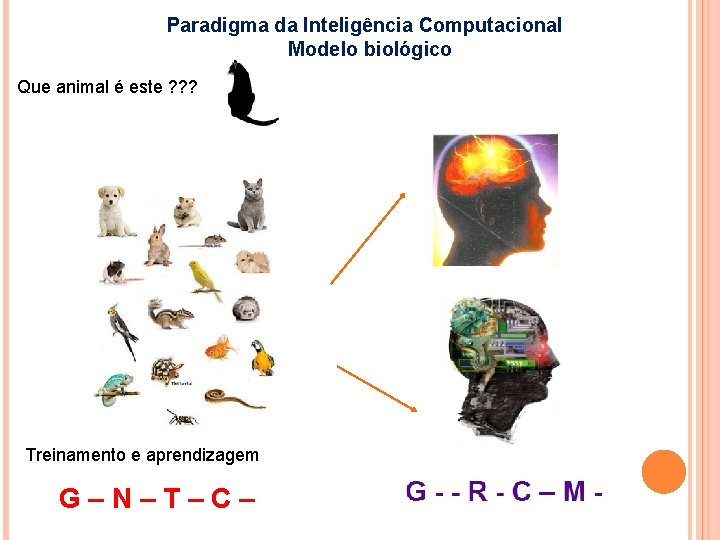
Paradigma da Inteligência Computacional Modelo biológico Que animal é este ? ? ? Treinamento e aprendizagem G–N–T–C–

Por que devemos estudar temas relativos a RNA?

Melhoramento Genético Passarei hoje por todo o teu rebanho, separando dele todos os salpicados e malhados, e todos os morenos entre os cordeiros, e os malhados e salpicados entre as cabras; e isto será o meu salário. Gênesis 30: 32 1866: Gregor Mendel, monge Austríaco, publicou as leis da hereditariedade baseado nos resultados de seus experimentos, iniciados em 1857, com ervilhas.

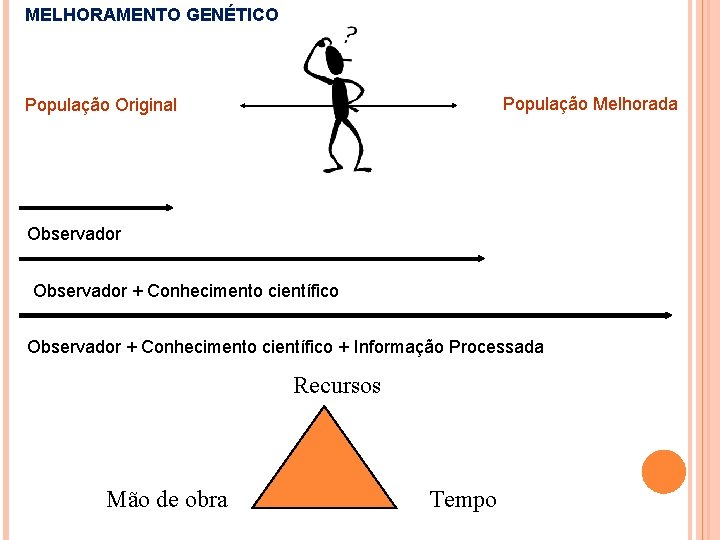
MELHORAMENTO GENÉTICO População Melhorada População Original Observador + Conhecimento científico + Informação Processada Recursos Mão de obra Tempo

IDENTIFICAÇÃO DE GENÓTIPOS SUPERIORES Ampla variabilidade A B C 10 9. 8 4. 2 Predição Classificação Pouca variabilidade

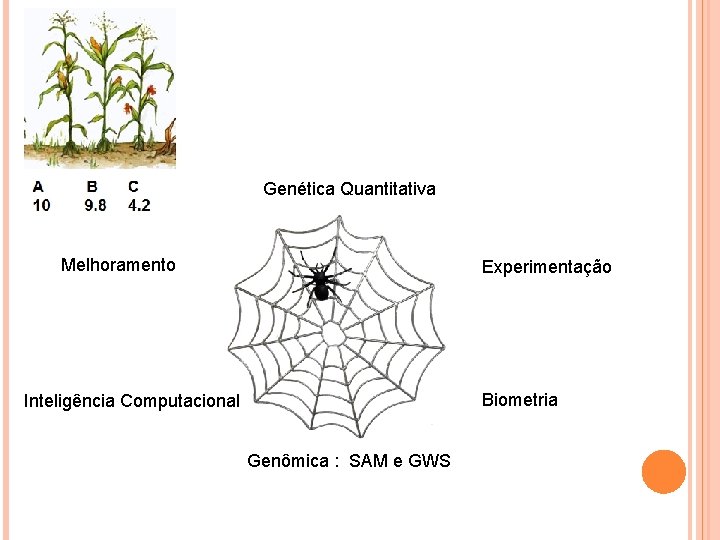
Genética Quantitativa Melhoramento Experimentação Biometria Inteligência Computacional Genômica : SAM e GWS

REDES NEURAIS: FUNDAMENTOS

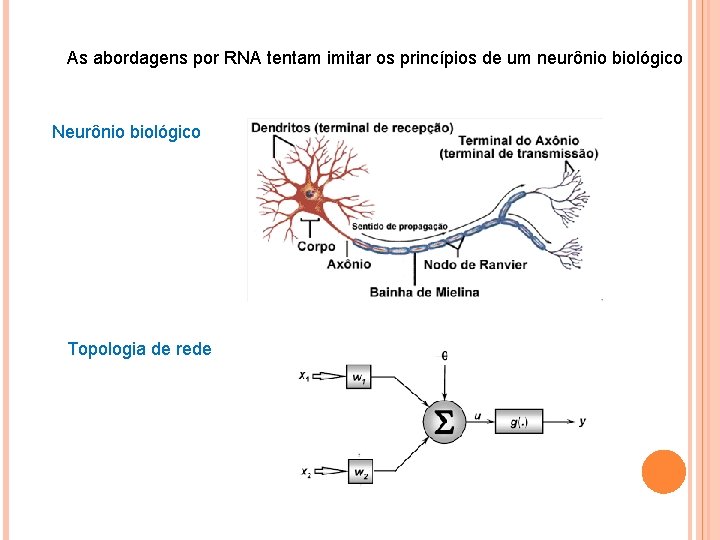
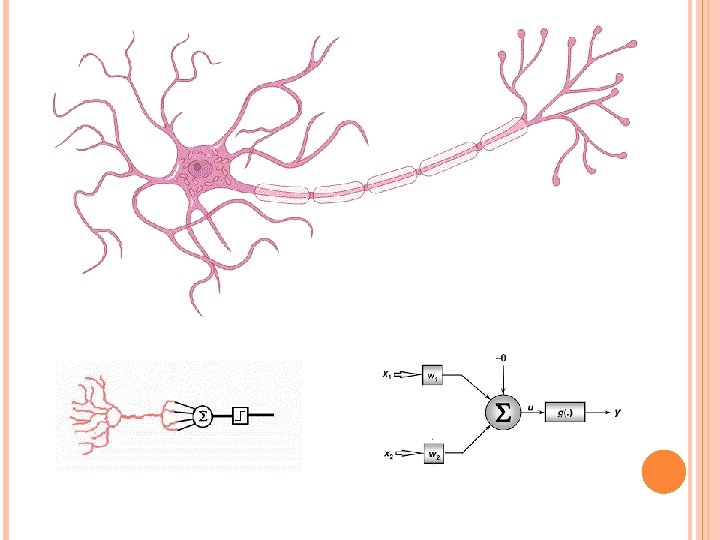
As abordagens por RNA tentam imitar os princípios de um neurônio biológico Neurônio biológico Topologia de rede

MODELO 1 - Mc. Culloch e Pitts Mc. Culloch era um psiquiatra e um neuroanatomista e Pitts era um matemático que foi trabalhar com Mc. Culloch na Universidade de Chicago, ambos fazendo parte de um dos primeiros grupos do mundo dedicado ao estudo da Biofísica Teórica, criado por Nicolas Rashevsky. Em 1943, o conhecimento sobre os neurônios biológicos era muito limitado. As bases iônicas e elétricas da atividade neuronal eram ainda incertas, porém já se sabia da existência de potenciais de ação e da sua natureza “tudo-ou-nada”. Mc. Culloch e Pitts propuseram um modelo de sistema neural em que as unidades básicas, os neurônios, são bastante simples no seu funcionamento.

1. Hipótese do modelo de MCP 1. A atividade de um neurônio é binária, ou seja, a cada instante o neurônio, ou está disparando (atividade = 1) ou não está disparando (atividade = 0); 2. A rede neural é constituída por linhas direcionadas, com pesos ajustáveis, ligando os neurônios. Essas linhas (inspiradas nas sinapses) podem ser excitatórias ou inibitórias (positivas ou negativas); 3. Cada neurônio tem um limiar fixo Ɵ, de maneira que ele só dispara se a entrada total chegando a ele, num dado instante, for maior ou igual a Ɵ, ; 4. A chegada de uma única sinapse inibitória num dado instante evita o disparo do neurônio, independentemente do número de sinapses excitatórias que estejam chegando conjuntamente com a sinapse inibitória; Uma restrição existente no modelo criado é que as redes desenvolvidas só conseguem implementar funções linearmente separáveis, ou seja, aquelas que se podem separar os padrões por meio de uma reta.

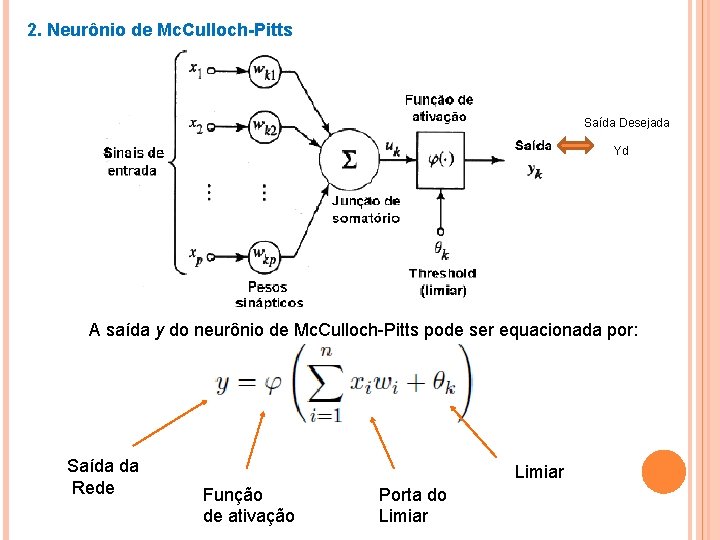
2. Neurônio de Mc. Culloch-Pitts Saída Desejada Yd A saída y do neurônio de Mc. Culloch-Pitts pode ser equacionada por: Saída da Rede Limiar Função de ativação Porta do Limiar

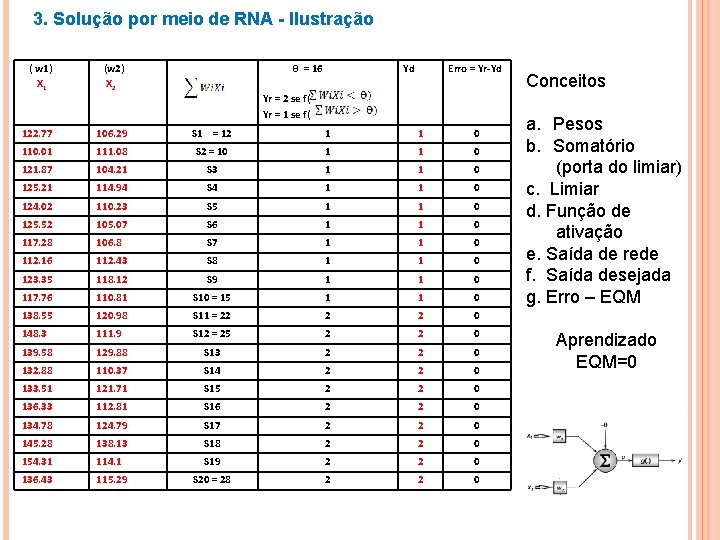
3. Solução por meio de RNA - Ilustração ( w 1) X 1 (w 2) X 2 θ = 16 Yd Erro = Yr-Yd Yr = 2 se f( Yr = 1 se f( 122. 77 106. 29 S 1 = 12 1 1 0 110. 01 111. 08 S 2 = 10 1 1 0 121. 87 104. 21 S 3 1 1 0 125. 21 114. 94 S 4 1 1 0 124. 02 110. 23 S 5 1 1 0 125. 52 105. 07 S 6 1 1 0 117. 28 106. 8 S 7 1 1 0 112. 16 112. 43 S 8 1 1 0 123. 35 118. 12 S 9 1 1 0 117. 76 110. 81 S 10 = 15 1 1 0 138. 55 120. 98 S 11 = 22 2 2 0 148. 3 111. 9 S 12 = 25 2 2 0 139. 58 129. 88 S 13 2 2 0 132. 88 110. 37 S 14 2 2 0 133. 51 121. 71 S 15 2 2 0 136. 33 112. 81 S 16 2 2 0 134. 78 124. 79 S 17 2 2 0 145. 28 138. 13 S 18 2 2 0 154. 31 114. 1 S 19 2 2 0 136. 43 115. 29 S 20 = 28 2 2 0 Conceitos a. Pesos b. Somatório (porta do limiar) c. Limiar d. Função de ativação e. Saída de rede f. Saída desejada g. Erro – EQM Aprendizado EQM=0

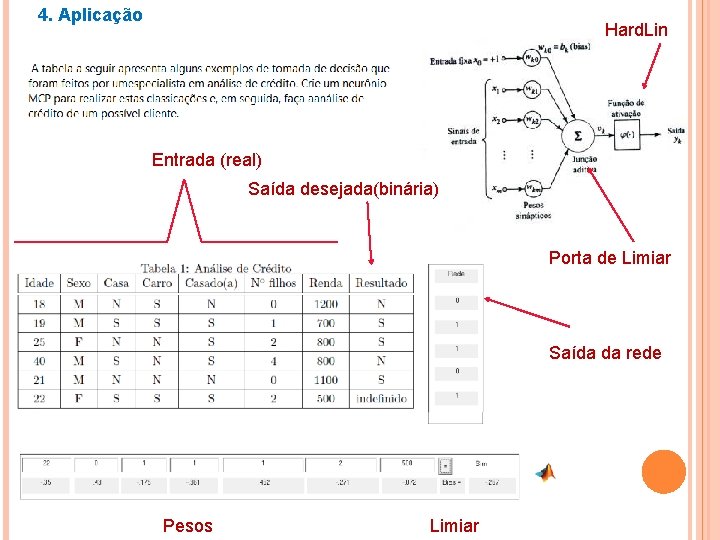
4. Aplicação Hard. Lin Entrada (real) Saída desejada(binária) Porta de Limiar Saída da rede Pesos Limiar

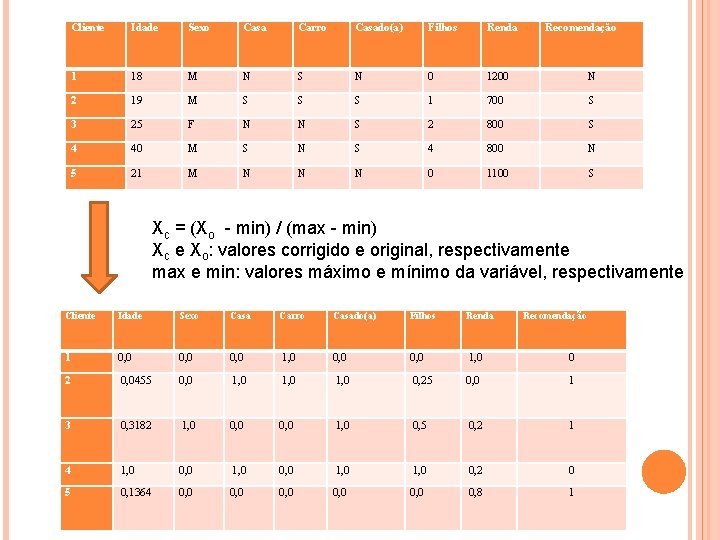
Cliente Idade Sexo Casa Carro Casado(a) Filhos Renda Recomendação 1 18 M N S N 0 1200 N 2 19 M S S S 1 700 S 3 25 F N N S 2 800 S 4 40 M S N S 4 800 N 5 21 M N N N 0 1100 S Xc = (Xo - min) / (max - min) Xc e Xo: valores corrigido e original, respectivamente max e min: valores máximo e mínimo da variável, respectivamente Cliente Idade Sexo Casa Carro Casado(a) Filhos Renda Recomendação 1 0, 0 1, 0 0, 0 1, 0 0 2 0, 0455 0, 0 1, 0 0, 25 0, 0 1 3 0, 3182 1, 0 0, 0 1, 0 0, 5 0, 2 1 4 1, 0 0, 0 1, 0 0, 2 0 5 0, 1364 0, 0 0, 0 0, 8 1

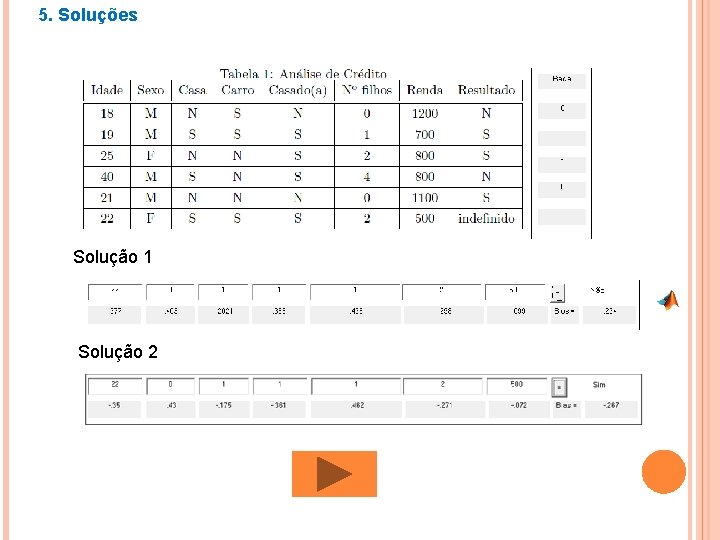
5. Soluções Solução 1 Solução 2

MODELO 2. Perceptron No final da década de 1950, Rosenblatt na Universidade de Cornell, criou uma genuína rede de múltiplos neurônios do tipo discriminadores lineares e chamou esta rede de perceptron. Perceptron pode ser visto como o tipo mais simples de rede neural feedforward: um classificador linear.

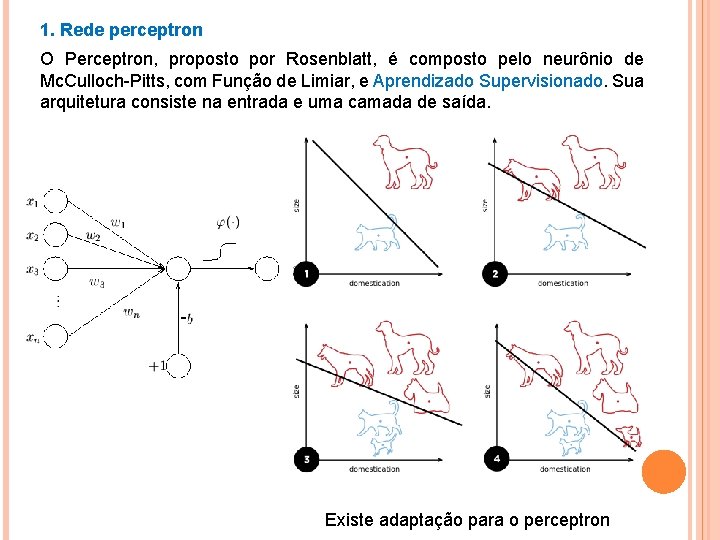
1. Rede perceptron O Perceptron, proposto por Rosenblatt, é composto pelo neurônio de Mc. Culloch-Pitts, com Função de Limiar, e Aprendizado Supervisionado. Sua arquitetura consiste na entrada e uma camada de saída. - Existe adaptação para o perceptron

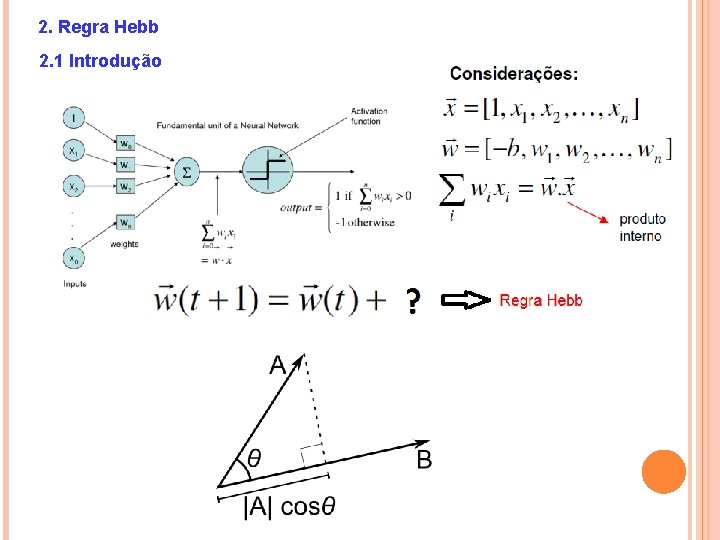
2. Regra Hebb 2. 1 Introdução

2. 3 Princípio da aprendizagem: Vetores de um grupo de treinamento são apresentados para a rede um após o outro. Se a saída da rede está correta, nenhuma mudança é feita. Por outro lado, os pesos e as inclinações são atualizados usando as regras de aprendizado do perceptron. Uma passagem inteira de treinamento de entrada de um vetor é chamada época.

2. 4 Correções nos Pesos - Aprendizagem Caso 1: Yd = 1 e Yr = 0, ou seja e = 1

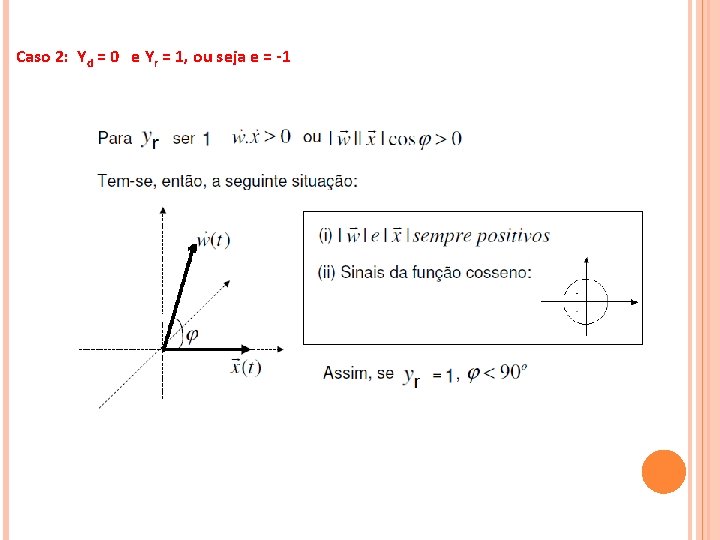
Caso 2: Yd = 0 e Yr = 1, ou seja e = -1

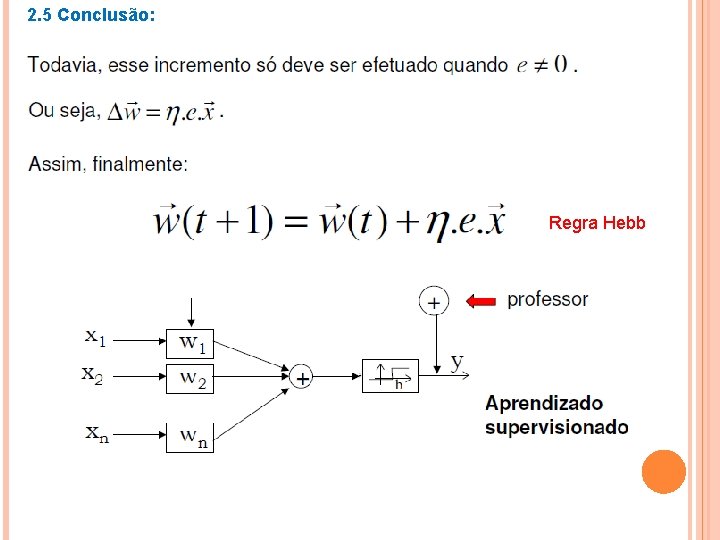
2. 5 Conclusão: Regra Hebb

3. Algoritmo • 1º Passo: inicializar pesos (Wi) e threshold(limiar – W 0). • 2º Passo: calcular (para cada j) a soma do limiar ( Wi. Xij). Aplicar a função de ativação e obter a saída de rede (Yrj). • 3º Passo: estimar o erro dado pela diferença entra a saída desejada (Ydj) e a saída de rede (Yrj). j = Ydj - Yrj • 4º Passo: atualizar o peso (Regra de aprendizagem). Esta atualização é feita através da fórmula: Wi( t + 1 ) = Wi ( t ) + j Xij, i = 0, 1, . . . v (v = número de entradas) j = 1, 2, . . . n (n = número de observações) t = 1, 2, . . . ep (ep = número de épocas) Ydj = +1 se entrada for da classe A e 0 se entrada for da classe B. Yrj = +1 se Wi. Xij >0 e 0 Wi. Xij <= 0. é uma fração menor que 1 (taxa de aprendizado) Critérios de parada: ep(t) : atingir o número máximo de épocas TEA(t): for inferior a taxa de erro mínima previamente estabelecida

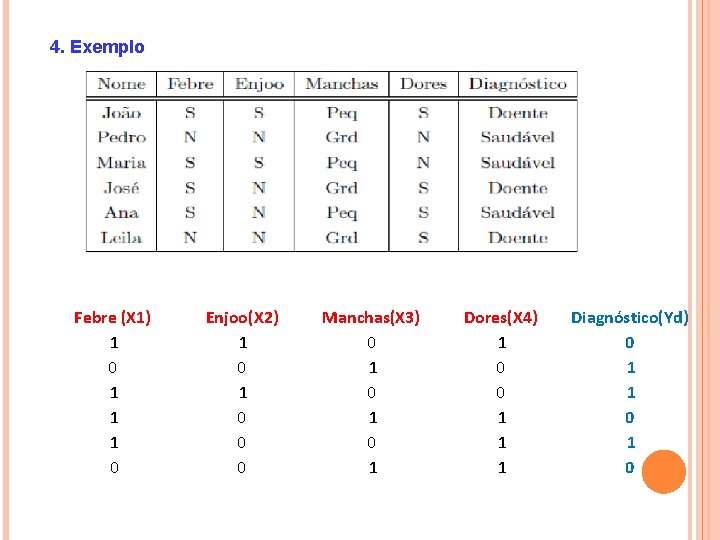
4. Exemplo Febre (X 1) 1 0 1 1 1 0 Enjoo(X 2) 1 0 0 0 Manchas(X 3) 0 1 0 1 Dores(X 4) 1 0 0 1 1 1 Diagnóstico(Yd) 0 1 1 0

Entradas Ind 1 2 3 4 5 6 ----------------------------------------X 0 -1 -1 -1 X 1 0 1 1 0 X 2 1 0 0 X 3 0 1 X 4 1 0 1 1 ----------------------------------------Saída Desejada ----------------------------------------Yd 0 1 0 ----------------------------------------Época : 1 Taxa de aprendizado: = 0. 1 Pesos: W 0 =. 324 W 1 = -. 238 W 2 =. 183 W 3 = -. 345 W 4 = -. 231 Yd 0 1 0 wixi -. 61 -. 669 -. 379 -1. 138 -. 793 -. 9 Yrede 0 0 0 Erro 0 1 0 ex: D 0 = -. 3 D 1 =. 2 D 2 =. 1 D 3 =. 1 D 4 =. 1

Época : 2 Pesos: W 0 =. 024 W 1 = -. 038 W 2 =. 283 W 3 = -. 245 W 4 = -. 131 Yd 0 1 1 0 1 0 wixi . 09 -. 269 . 221 -. 438 -. 193 -. 4 Yrede 1 0 0 Erro -1 1 0 0 1 0 ex: D 0 = -. 1 D 1 =. 0 D 2 = -. 1 D 3 =. 1 D 4 =. 0 Época : 3 Pesos: W 0 = -. 076 W 1 = -. 038 W 2 =. 183 W 3 = -. 145 W 4 = -. 131 Yd 0 1 0 wixi . 09 -. 069 . 221 -. 238 -. 093 -. 2 Yrede 1 0 0 Erro -1 1 0 0 1 0 ex: D 0 = -. 1 D 1 =. 0 D 2 = -. 1 D 3 =. 1 D 4 =. 0 Época : 4 Pesos: W 0 = -. 176 W 1 = -. 038 W 2 =. 083 W 3 = -. 045 W 4 = -. 131 Yd 0 1 1 0 1 0 wixi . 09 . 131 . 221 -. 038 . 007 . 0 Yrede 1 1 0 1 0 Erro -1 0 0 ex: D 0 =. 1 D 1 = -. 1 D 2 = -. 1 D 3 =. 0 D 4 = -. 1

Época : 5 Pesos: W 0 = -. 076 W 1 = -. 138 W 2 = -. 017 W 3 = -. 045 W 4 = -. 231 Yd 0 1 1 0 1 0 wixi -. 31 . 031 -. 079 -. 338 -. 293 -. 2 Yrede 0 1 0 0 0 Erro 0 1 0 ex: D 0 = -. 2 D 1 =. 2 D 2 =. 1 D 3 =. 0 D 4 =. 1 Época : 6 Pesos: W 0 = -. 276 W 1 =. 062 W 2 =. 083 W 3 = -. 045 W 4 = -. 131 Yd 0 1 1 0 1 0 wixi . 29 . 231 . 421 . 162 . 207 . 1 Yrede 1 1 1 Erro -1 0 0 -1 0 -1 ex: D 0 =. 3 D 1 = -. 2 D 2 = -. 1 D 3 = -. 2 D 4 = -. 3 Época : 7 Pesos: W 0 =. 024 W 1 = -. 138 W 2 = -. 017 W 3 = -. 245 W 4 = -. 431 Yd 0 1 1 0 wixi -. 61 -. 269 -. 179 -. 838 -. 593 -. 7 Yrede 0 0 0 Erro 0 1 1 0 ex: D 0 = -. 3 D 1 =. 2 D 2 =. 1 D 3 =. 1 D 4 =. 1

Época : 8 Pesos: W 0 = -. 276 W 1 =. 062 W 2 =. 083 W 3 = -. 145 W 4 = -. 331 Yd 0 1 0 wixi . 09 . 131 . 421 -. 138 . 007 -. 2 Yrede 1 1 0 Erro -1 0 0 0 ex: D 0 =. 1 D 1 = -. 1 D 2 = -. 1 D 3 =. 0 D 4 = -. 1 Época : 9 Pesos: W 0 = -. 176 W 1 = -. 038 W 2 = -. 017 W 3 = -. 145 W 4 = -. 431 Yd 0 1 0 1 0 wixi -. 31 . 031 . 121 -. 438 -. 293 -. 4 Yrede 0 1 0 0 0 Erro 0 0 1 0 ex: D 0 = -. 1 D 1 =. 1 D 2 =. 0 D 3 =. 0 D 4 =. 1 Época : 10 Pesos: W 0 = -. 276 W 1 =. 062 W 2 = -. 017 W 3 = -. 145 W 4 = -. 331 Yd 0 1 0 wixi -. 01 . 131 . 321 -. 138 . 007 -. 2 Yrede 0 1 0 Erro 0 0 0 0 ex: D 0 =. 0 D 1 =. 0 D 2 =. 0 D 3 =. 0 D 4 =. 0

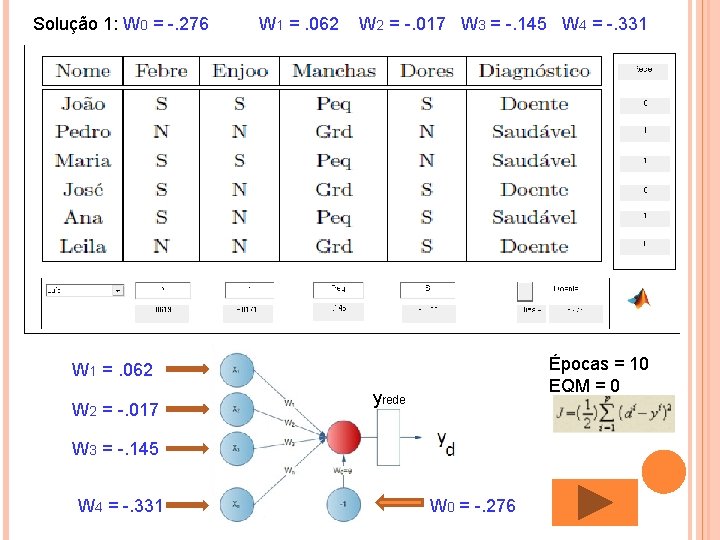
Solução 1: W 0 = -. 276 W 1 =. 062 W 2 = -. 017 W 3 = -. 145 W 4 = -. 331 Épocas = 10 EQM = 0 W 1 =. 062 W 2 = -. 017 yrede W 3 = -. 145 W 4 = -. 331 W 0 = -. 276

Solução 2: W 0 = -. 276 W 1 =. 062 W 2 = -. 017 W 3 = -. 145 W 4 = -. 331

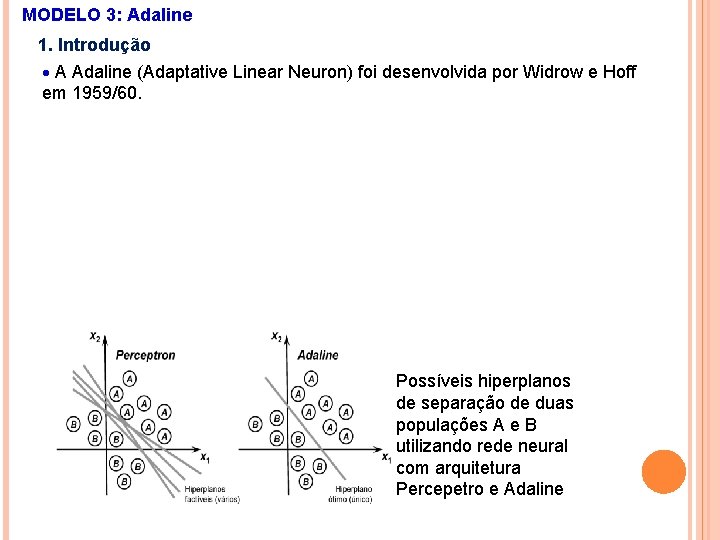
MODELO 3: Adaline 1. Introdução A Adaline (Adaptative Linear Neuron) foi desenvolvida por Widrow e Hoff em 1959/60. Possíveis hiperplanos de separação de duas populações A e B utilizando rede neural com arquitetura Percepetro e Adaline

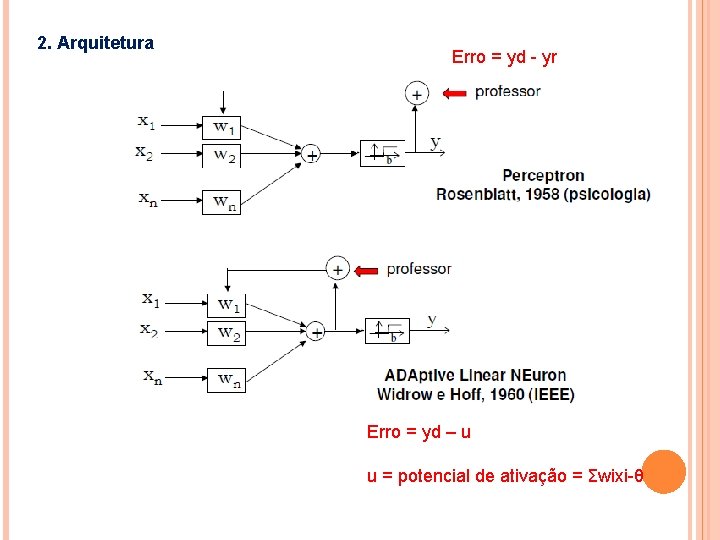
2. Arquitetura Erro = yd - yr Erro = yd – u u = potencial de ativação = Σwixi-θ

3. Princípios do método do gradiente descendente t x 0 1 2 3 4 5 5 2, 6 2, 12 2, 024 2, 0048 2, 00096 -2. 4 -0, 48 -0, 096 -0. 0192 -0, 00384 -0, 000768

4. Regra de Aprendizagem Função de custo Derivada Regra de aprendizagem wi( t + 1) = wi(t) + j xij

5. Algoritmo

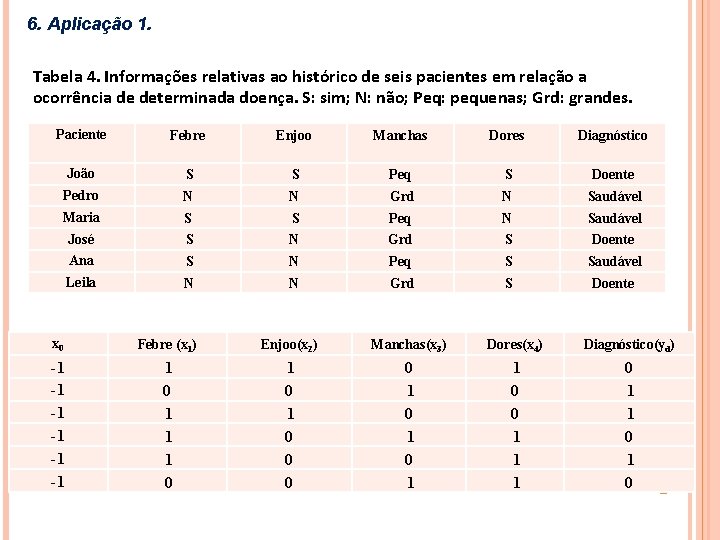
6. Aplicação 1. Tabela 4. Informações relativas ao histórico de seis pacientes em relação a ocorrência de determinada doença. S: sim; N: não; Peq: pequenas; Grd: grandes. Paciente Febre Enjoo Manchas Dores Diagnóstico João S S Peq S Doente Pedro N N Grd N Saudável Maria S S Peq N Saudável José S N Grd S Doente Ana S N Peq S Saudável Leila N N Grd S Doente x 0 Febre (x 1) Enjoo(x 2) Manchas(x 3) Dores(x 4) Diagnóstico(yd) -1 -1 -1 1 0 1 1 1 0 0 0 0 1 1 0 0 1 1 1 0 1 0

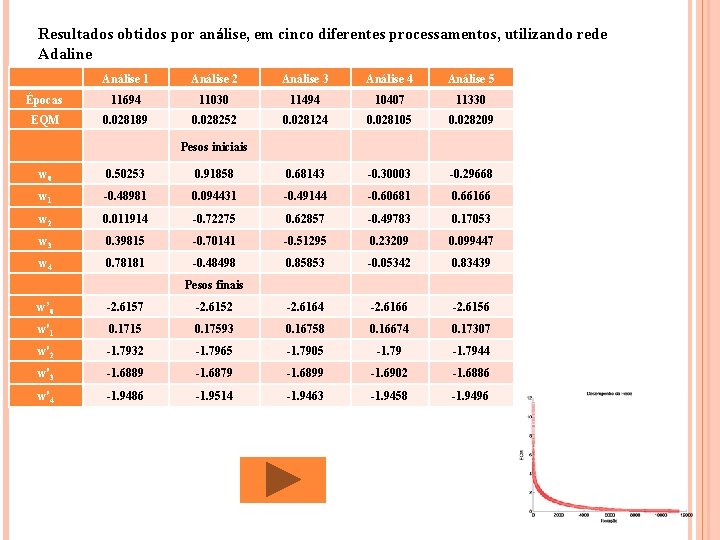
Resultados obtidos por análise, em cinco diferentes processamentos, utilizando rede Adaline Análise 1 Análise 2 Análise 3 Análise 4 Análise 5 Épocas 11694 11030 11494 10407 11330 EQM 0. 028189 0. 028252 0. 028124 0. 028105 0. 028209 Pesos iniciais w 0 0. 50253 0. 91858 0. 68143 -0. 30003 -0. 29668 w 1 -0. 48981 0. 094431 -0. 49144 -0. 60681 0. 66166 w 2 0. 011914 -0. 72275 0. 62857 -0. 49783 0. 17053 w 3 0. 39815 -0. 70141 -0. 51295 0. 23209 0. 099447 w 4 0. 78181 -0. 48498 0. 85853 -0. 05342 0. 83439 Pesos finais w’ 0 -2. 6157 -2. 6152 -2. 6164 -2. 6166 -2. 6156 w'1 0. 1715 0. 17593 0. 16758 0. 16674 0. 17307 w'2 -1. 7932 -1. 7965 -1. 7905 -1. 7944 w'3 -1. 6889 -1. 6879 -1. 6899 -1. 6902 -1. 6886 w'4 -1. 9486 -1. 9514 -1. 9463 -1. 9458 -1. 9496

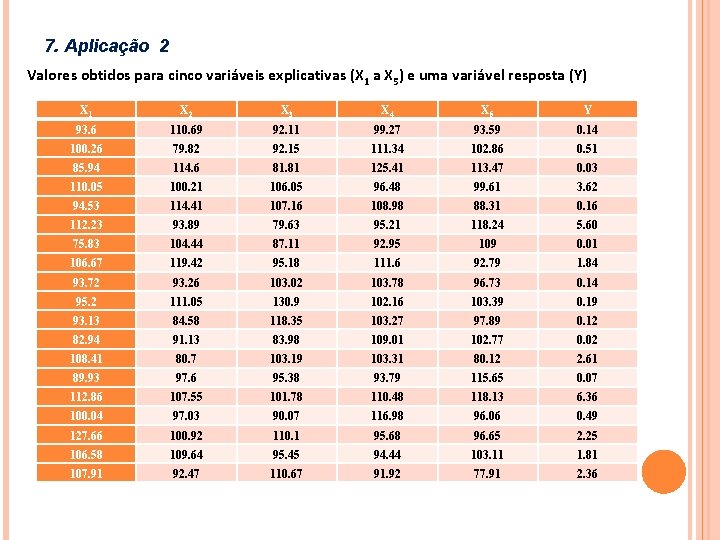
7. Aplicação 2 Valores obtidos para cinco variáveis explicativas (X 1 a X 5) e uma variável resposta (Y) X 1 X 2 X 3 X 4 X 5 Y 93. 6 110. 69 92. 11 99. 27 93. 59 0. 14 100. 26 79. 82 92. 15 111. 34 102. 86 0. 51 85. 94 114. 6 81. 81 125. 41 113. 47 0. 03 110. 05 100. 21 106. 05 96. 48 99. 61 3. 62 94. 53 114. 41 107. 16 108. 98 88. 31 0. 16 112. 23 93. 89 79. 63 95. 21 118. 24 5. 60 75. 83 104. 44 87. 11 92. 95 109 0. 01 106. 67 119. 42 95. 18 111. 6 92. 79 1. 84 93. 72 93. 26 103. 02 103. 78 96. 73 0. 14 95. 2 111. 05 130. 9 102. 16 103. 39 0. 19 93. 13 84. 58 118. 35 103. 27 97. 89 0. 12 82. 94 91. 13 83. 98 109. 01 102. 77 0. 02 108. 41 80. 7 103. 19 103. 31 80. 12 2. 61 89. 93 97. 6 95. 38 93. 79 115. 65 0. 07 112. 86 107. 55 101. 78 110. 48 118. 13 6. 36 100. 04 97. 03 90. 07 116. 98 96. 06 0. 49 127. 66 100. 92 110. 1 95. 68 96. 65 2. 25 106. 58 109. 64 95. 45 94. 44 103. 11 1. 81 107. 91 92. 47 110. 67 91. 92 77. 91 2. 36

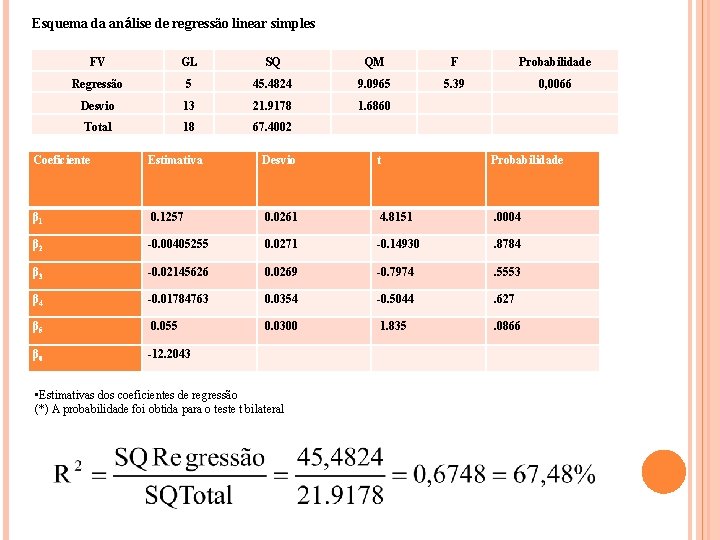
Esquema da análise de regressão linear simples FV GL SQ QM F Probabilidade Regressão 5 45. 4824 9. 0965 5. 39 0, 0066 Desvio 13 21. 9178 1. 6860 Total 18 67. 4002 Coeficiente Estimativa Desvio t Probabilidade β 1 0. 1257 0. 0261 4. 8151 . 0004 β 2 -0. 00405255 0. 0271 -0. 14930 . 8784 β 3 -0. 02145626 0. 0269 -0. 7974 . 5553 β 4 -0. 01784763 0. 0354 -0. 5044 . 627 β 5 0. 055 0. 0300 1. 835 . 0866 β 0 -12. 2043 • Estimativas dos coeficientes de regressão (*) A probabilidade foi obtida para o teste t bilateral

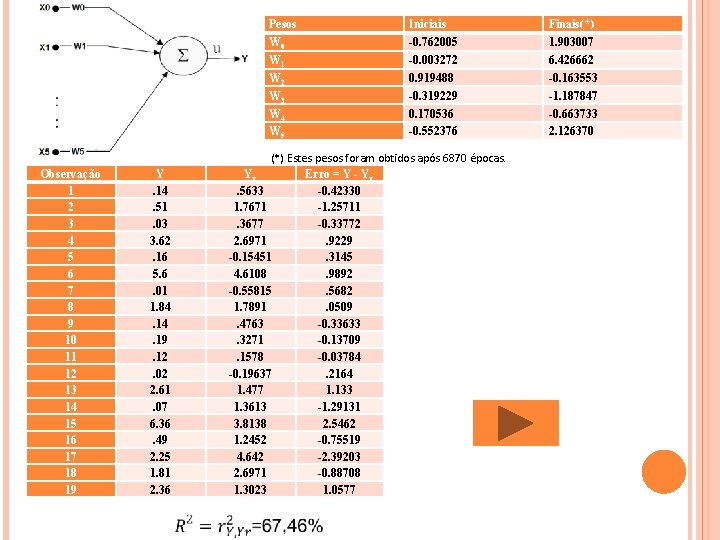
Pesos W 0 W 1 W 2 W 3 W 4 W 5 Observação 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 Y. 14. 51. 03 3. 62. 16 5. 6. 01 1. 84. 19. 12. 02 2. 61. 07 6. 36. 49 2. 25 1. 81 2. 36 Iniciais -0. 762005 -0. 003272 0. 919488 -0. 319229 0. 170536 -0. 552376 (*) Estes pesos foram obtidos após 6870 épocas. Yr Erro = Y - Yr. 5633 -0. 42330 1. 7671 -1. 25711. 3677 -0. 33772 2. 6971. 9229 -0. 15451. 3145 4. 6108. 9892 -0. 55815. 5682 1. 7891. 0509. 4763 -0. 33633. 3271 -0. 13709. 1578 -0. 03784 -0. 19637. 2164 1. 477 1. 133 1. 3613 -1. 29131 3. 8138 2. 5462 1. 2452 -0. 75519 4. 642 -2. 39203 2. 6971 -0. 88708 1. 3023 1. 0577 Finais(*) 1. 903007 6. 426662 -0. 163553 -1. 187847 -0. 663733 2. 126370

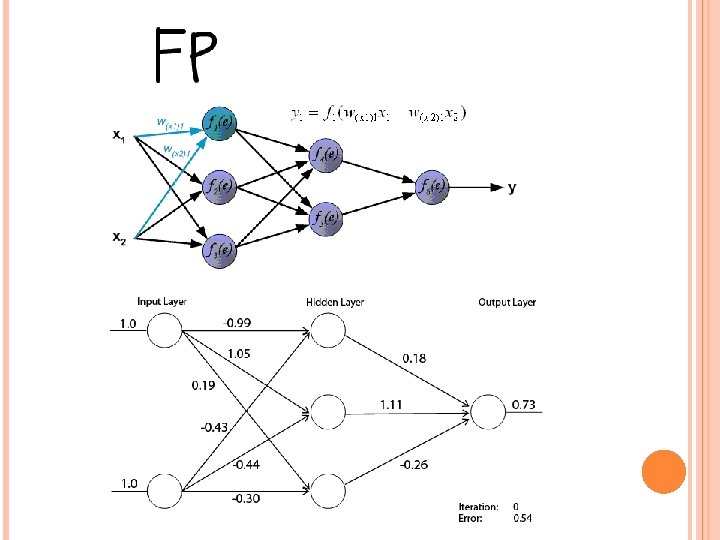
MODELO 4: Perceptron Multicamadas (MLP) 1 Histórico -Fundamentou-se no desenvolvimento do algoritmo de treinamento backpropagation. -Foi formulado por Rumelhart, Hinton e Williams em 1986, RUMELHART et. al. (1986), precedido por propostas semelhantes ocorridas nos anos 70 e 80, WERBOS (1974); PARKER (1985) - Mostrou que é possível treinar eficientemente Redes Neurais com camadas intermediárias

MINSKY & PAPERT (1969) analisaram matematicamente o Perceptron e demostraram que redes de uma camada não são capazes de solucionar problemas que não sejam linearmente separáveis. Como não acreditavam na possibilidade de se construir um método de treinamento para redes com mais de uma camada, eles concluíram que as Redes Neurais seriam sempre suscetíveis a essa limitação.

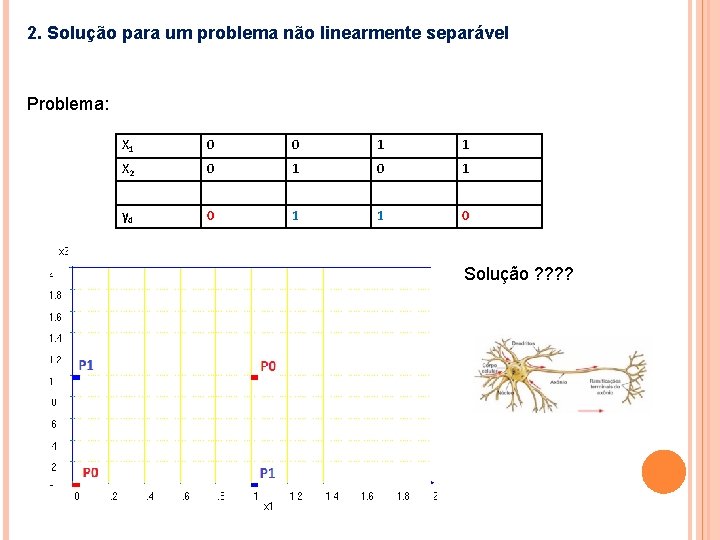
2. Solução para um problema não linearmente separável Problema: X 1 0 0 1 1 X 2 0 1 yd 0 1 1 0 Solução ? ?

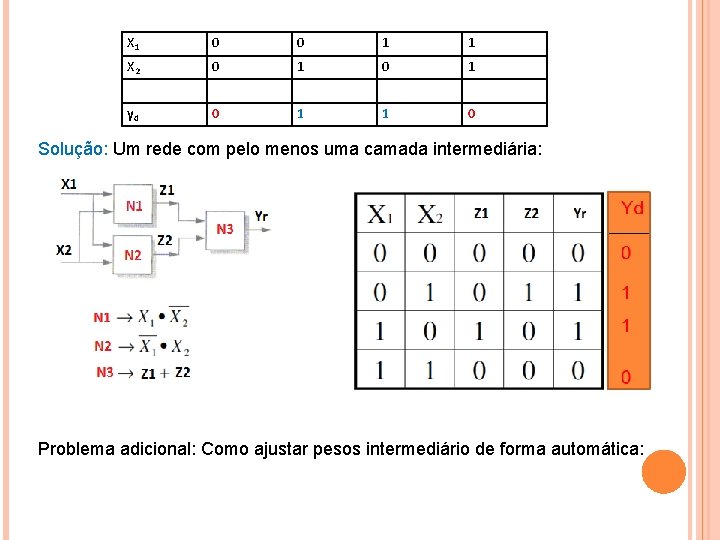
X 1 0 0 1 1 X 2 0 1 yd 0 1 1 0 Solução: Um rede com pelo menos uma camada intermediária: Problema adicional: Como ajustar pesos intermediário de forma automática:

3. Estrutura de rede do MLP • Cada camada recebe dados da camada imediatamente inferior e envia para a camada subseqüente. • Não existem conexões entre elementos da mesma camada. • Cada camada tem uma função específica. • A camada de saída recebe os estímulos das camadas intermediárias e constrói o padrão que será a resposta. • As camadas intermediárias funcionam como extratoras de características, seus pesos são uma codificação de características apresentadas nos padrões de entrada e permitem que a rede crie sua própria representação, mais rica e complexa, do problema.

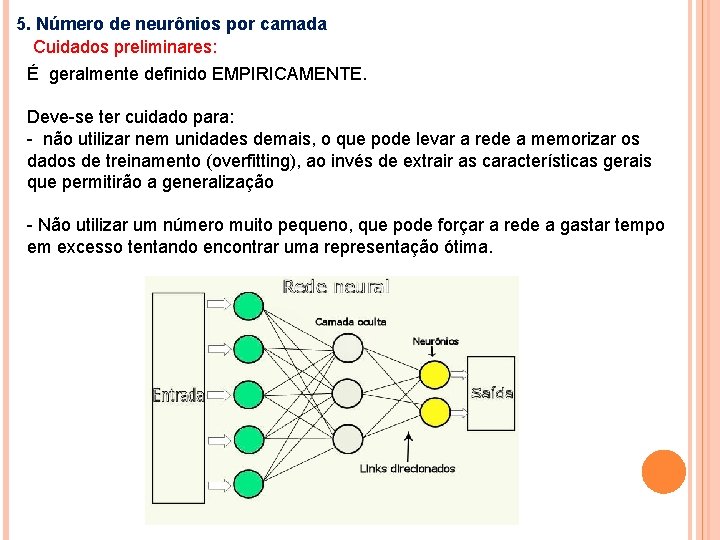
4. Número de camadas intermediárias (ocultas) • Apenas uma camada intermediária é suficiente para aproximar qualquer função contínua - CYBENKO (1989). • Para a resolução de problemas de classificação uma rede neural com uma camada escondida é mais que suficiente. • CYBENKO (1988) provou, a partir de extensões do Teorema de Kolmogoroff, que são necessárias no máximo duas camadas intermediárias, com um número suficiente de unidades (neurônios) por camada, para se produzirem quaisquer mapeamentos (ajuste). • Para problemas muito complexos a utilização de três camadas intermediárias pode facilitar o treinamento ou melhorar a capacidade de generalização das redes MLP.

5. Número de neurônios por camada Cuidados preliminares: É geralmente definido EMPIRICAMENTE. Deve-se ter cuidado para: - não utilizar nem unidades demais, o que pode levar a rede a memorizar os dados de treinamento (overfitting), ao invés de extrair as características gerais que permitirão a generalização - Não utilizar um número muito pequeno, que pode forçar a rede a gastar tempo em excesso tentando encontrar uma representação ótima.

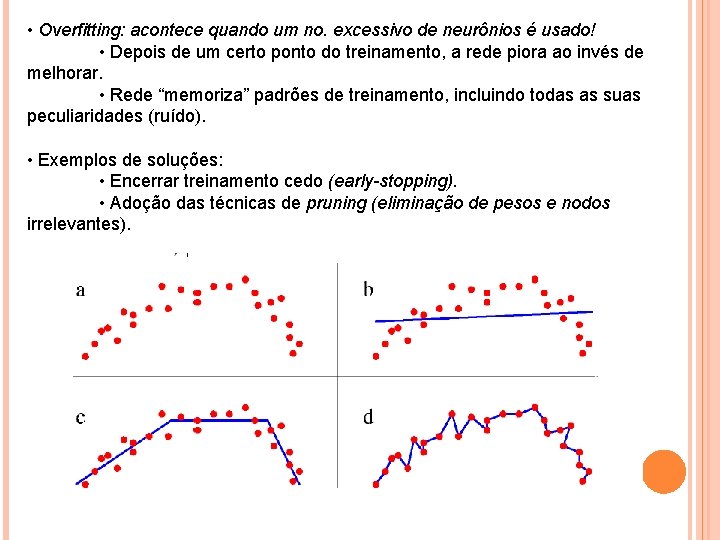
• Overfitting: acontece quando um no. excessivo de neurônios é usado! • Depois de um certo ponto do treinamento, a rede piora ao invés de melhorar. • Rede “memoriza” padrões de treinamento, incluindo todas as suas peculiaridades (ruído). • Exemplos de soluções: • Encerrar treinamento cedo (early-stopping). • Adoção das técnicas de pruning (eliminação de pesos e nodos irrelevantes).

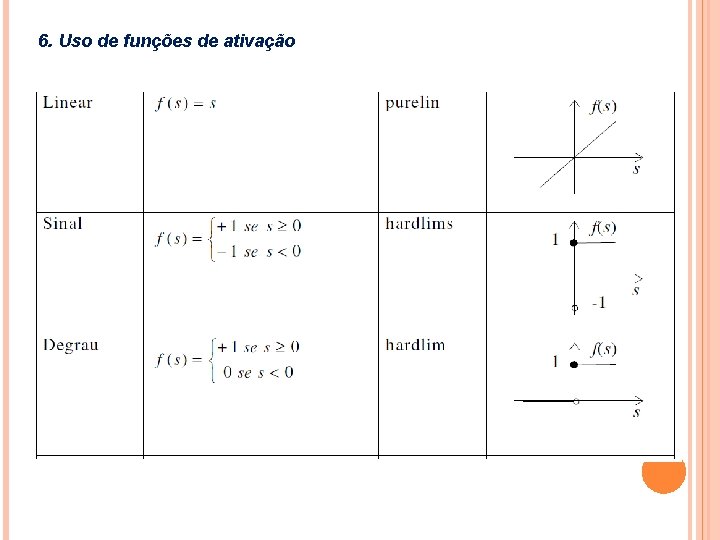
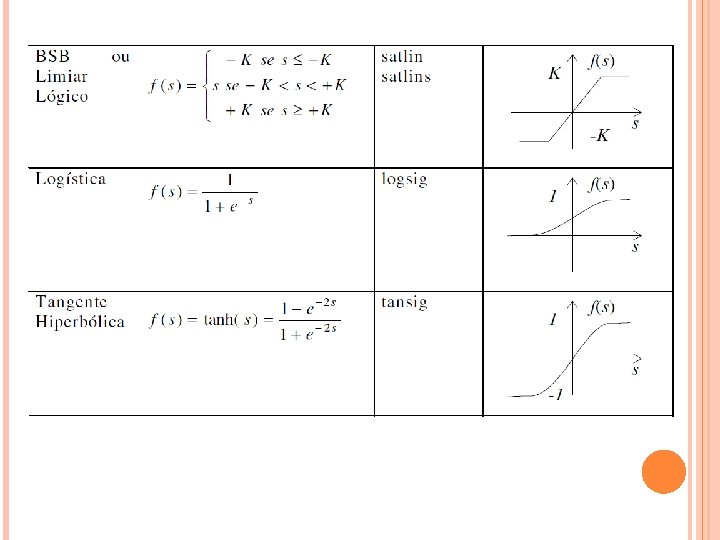
6. Uso de funções de ativação

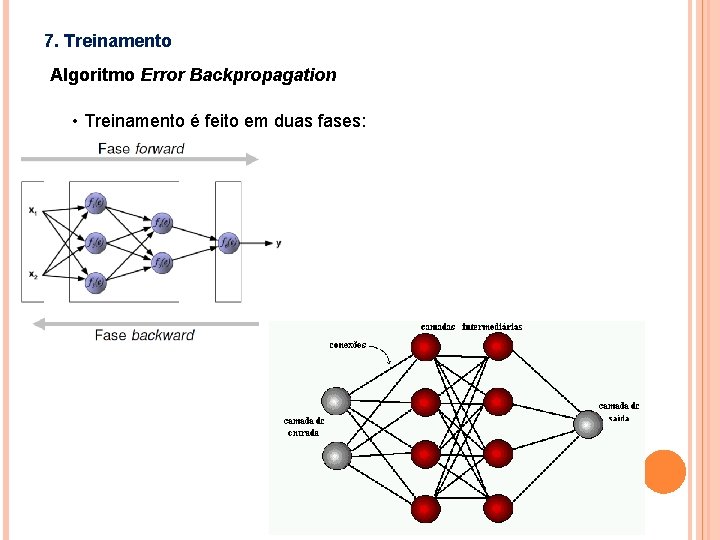
7. Treinamento Algoritmo Error Backpropagation • Treinamento é feito em duas fases:

Considerações finais: Fases do projeto de MLPs • Estudo do problema • Construção de um conjunto de treinamento • Conjunto de dados para validação • Conjunto de dados para teste • Escolha de uma arquitetura – Número de camadas ocultas – Número de neurônios por camada - Funções de ativação • Escolha de um algoritmo de aprendizado • Parâmetros a se ajustar - Número de épocas - Erro quadrático médio - Critério de otimização A seleção dos parâmetros da rede é um processo tão pouco compreendido que é muitas vezes chamado de “magia negra”. Pequenas diferenças nestes parâmetros podem levar a grandes diferenças tanto no tempo de treinamento como na generalização obtida.