Priority Queues 2014 Goodrich Tamassia Goldwasser Priority Queues

Priority Queues © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 1

Priority Queue ADT q q q A priority queue stores a collection of entries Each entry is a pair (key, value) Main methods of the Priority Queue ADT n n insert(k, v) inserts an entry with key k and value v remove. Min() removes and returns the entry with smallest key, or null if the priority queue is empty © 2014 Goodrich, Tamassia, Goldwasser q Additional methods n n q Priority Queues min() returns, but does not remove, an entry with smallest key, or null if the priority queue is empty size(), is. Empty() Applications: n n n Standby flyers Auctions Stock market 2

Example q A sequence of priority queue methods: © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 3

Entry ADT q q q An entry in a priority queue is simply a keyvalue pair Priority queues store entries to allow for efficient insertion and removal based on keys Methods: n n get. Key: returns the key for this entry get. Value: returns the value associated with this entry © 2014 Goodrich, Tamassia, Goldwasser q As a Java interface: /** * Interface for a key-value * pair entry **/ public interface Entry<K, V> { K get. Key(); V get. Value(); } Priority Queues 4

Total Order Relations q q Keys in a priority queue can be arbitrary objects on which an order is defined Two distinct entries in a priority queue can have the same key © 2014 Goodrich, Tamassia, Goldwasser q Mathematical concept of total order relation n n n Comparability property: either x y or y x Antisymmetric property: x y and y x x = y Transitive property: x y and y z x z Priority Queues 5

Comparator ADT q q A comparator encapsulates the action of comparing two objects according to a given total order relation A generic priority queue uses an auxiliary comparator The comparator is external to the keys being compared When the priority queue needs to compare two keys, it uses its comparator © 2014 Goodrich, Tamassia, Goldwasser q q Primary method of the Comparator ADT compare(a, b): returns an integer i such that n n Priority Queues i < 0 if a < b, i = 0 if a = b i > 0 if a > b An error occurs if a and b cannot be compared. 6

Example Comparator q Lexicographic comparison of 2 -D points: /** Comparator for 2 D points under the standard lexicographic order. */ public class Lexicographic implements Comparator { int xa, ya, xb, yb; public int compare(Object a, Object b) throws Class. Cast. Exception { xa = ((Point 2 D) a). get. X(); ya = ((Point 2 D) a). get. Y(); xb = ((Point 2 D) b). get. X(); yb = ((Point 2 D) b). get. Y(); if (xa != xb) return (xb - xa); else return (yb - ya); } } © 2014 Goodrich, Tamassia, Goldwasser q Point objects: /** Class representing a point in the plane with integer coordinates */ public class Point 2 D { protected int xc, yc; // coordinates public Point 2 D(int x, int y) { xc = x; yc = y; } public int get. X() { return xc; } public int get. Y() { return yc; } } Priority Queues 7

Sequence-based Priority Queue q Implementation with an unsorted list 4 q 5 2 3 1 Performance: n n q 1 q insert takes O(1) time since we can insert the item at the beginning or end of the sequence remove. Min and min take O(n) time since we have to traverse the entire sequence to find the smallest key © 2014 Goodrich, Tamassia, Goldwasser Implementation with a sorted list Priority Queues 2 3 4 5 Performance: n n insert takes O(n) time since we have to find the place where to insert the item remove. Min and min take O(1) time, since the smallest key is at the beginning 8

Unsorted List Implementation © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 9

Unsorted List Implementation, 2 © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 10

Sorted List Implementation © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 11

Sorted List Implementation, 2 © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 12

Priority Queue Sorting q q We can use a priority queue Algorithm PQ-Sort(S, C) Input list S, comparator C for the to sort a list of comparable elements of S elements Output list S sorted in increasing 1. Insert the elements order according to C one by one with a series of insert operations P priority queue with comparator C 2. Remove the elements in sorted order with a series while S. is. Empty () of remove. Min operations e S. remove(S. first ()) The running time of this P. insert (e, ) sorting method depends on while P. is. Empty() the priority queue e P. remove. Min(). get. Key() implementation S. add. Last(e) © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 13

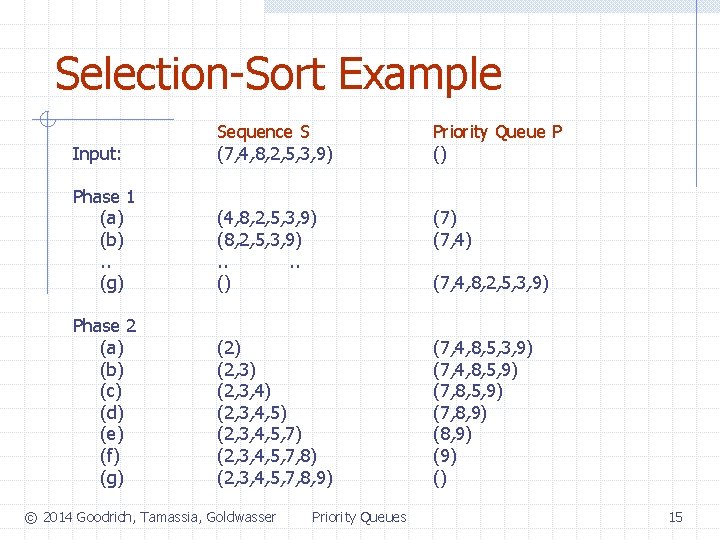
Selection-Sort q q Selection-sort is the variation of PQ-sort where the priority queue is implemented with an unsorted sequence Running time of Selection-sort: 1. Inserting the elements into the priority queue with n insert operations takes O(n) time 2. Removing the elements in sorted order from the priority queue with n remove. Min operations takes time proportional to q 1 + 2 + …+ n Selection-sort runs in O(n 2) time © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 14

Selection-Sort Example Input: Sequence S (7, 4, 8, 2, 5, 3, 9) Priority Queue P () Phase 1 (a) (b). . (g) (4, 8, 2, 5, 3, 9) (8, 2, 5, 3, 9). . () (7, 4) Phase 2 (a) (b) (c) (d) (e) (f) (g) (2, 3) (2, 3, 4, 5) (2, 3, 4, 5, 7, 8) (2, 3, 4, 5, 7, 8, 9) (7, 4, 8, 5, 3, 9) (7, 4, 8, 5, 9) (7, 8, 9) (9) () © 2014 Goodrich, Tamassia, Goldwasser Priority Queues (7, 4, 8, 2, 5, 3, 9) 15

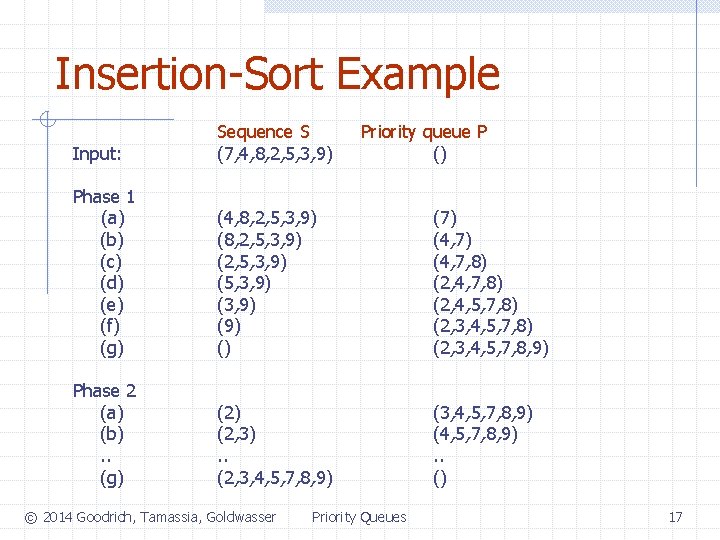
Insertion-Sort q q Insertion-sort is the variation of PQ-sort where the priority queue is implemented with a sorted sequence Running time of Insertion-sort: 1. Inserting the elements into the priority queue with n insert operations takes time proportional to 1 + 2 + …+ n 2. q Removing the elements in sorted order from the priority queue with a series of n remove. Min operations takes O(n) time Insertion-sort runs in O(n 2) time © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 16

Insertion-Sort Example Input: Sequence S (7, 4, 8, 2, 5, 3, 9) Phase 1 (a) (b) (c) (d) (e) (f) (g) (4, 8, 2, 5, 3, 9) (2, 5, 3, 9) (3, 9) () (7) (4, 7, 8) (2, 4, 5, 7, 8) (2, 3, 4, 5, 7, 8, 9) Phase 2 (a) (b). . (g) (2, 3). . (2, 3, 4, 5, 7, 8, 9) (4, 5, 7, 8, 9). . () © 2014 Goodrich, Tamassia, Goldwasser Priority queue P () Priority Queues 17

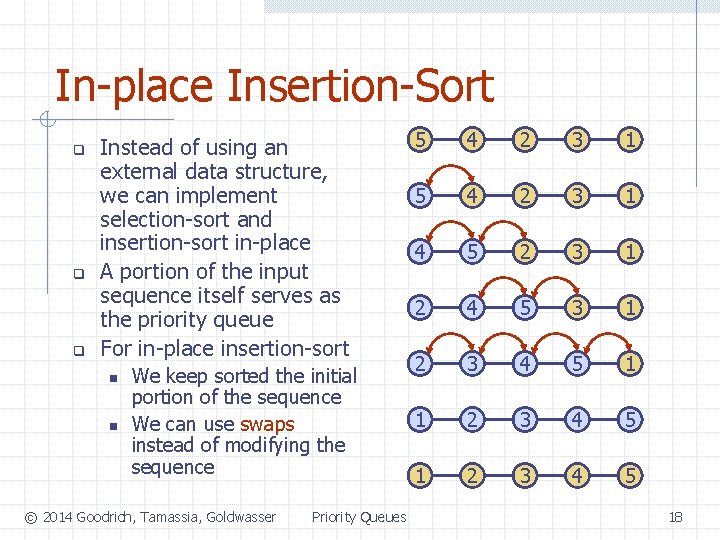
In-place Insertion-Sort q q q Instead of using an external data structure, we can implement selection-sort and insertion-sort in-place A portion of the input sequence itself serves as the priority queue For in-place insertion-sort n n We keep sorted the initial portion of the sequence We can use swaps instead of modifying the sequence © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 5 4 2 3 1 4 5 2 3 1 2 4 5 3 1 2 3 4 5 18

Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Heaps 2 5 9 © 2014 Goodrich, Tamassia, Goldwasser 6 7 Heaps 19

Recall Priority Queue ADT q q q A priority queue stores a collection of entries Each entry is a pair (key, value) Main methods of the Priority Queue ADT n n q insert(k, v) inserts an entry with key k and value v remove. Min() removes and returns the entry with smallest key © 2014 Goodrich, Tamassia, Goldwasser Additional methods Applications: n n n 20 min() returns, but does not remove, an entry with smallest key size(), is. Empty() Standby flyers Auctions Stock market Heaps

Recall PQ Sorting q We use a priority queue n Insert the elements with a series of insert operations n Remove the elements in sorted order with a series of remove. Min operations q The running time depends on the priority queue implementation: n n q Unsorted sequence gives selection-sort: O(n 2) time Sorted sequence gives insertion-sort: O(n 2) time Can we do better? © 2014 Goodrich, Tamassia, Goldwasser Algorithm PQ-Sort(S, C) Input sequence S, comparator C for the elements of S Output sequence S sorted in increasing order according to C P priority queue with comparator C while S. is. Empty () e S. remove (S. first ()) P. insert (e, e) while P. is. Empty() e P. remove. Min(). get. Key() S. add. Last(e) 21 Heaps

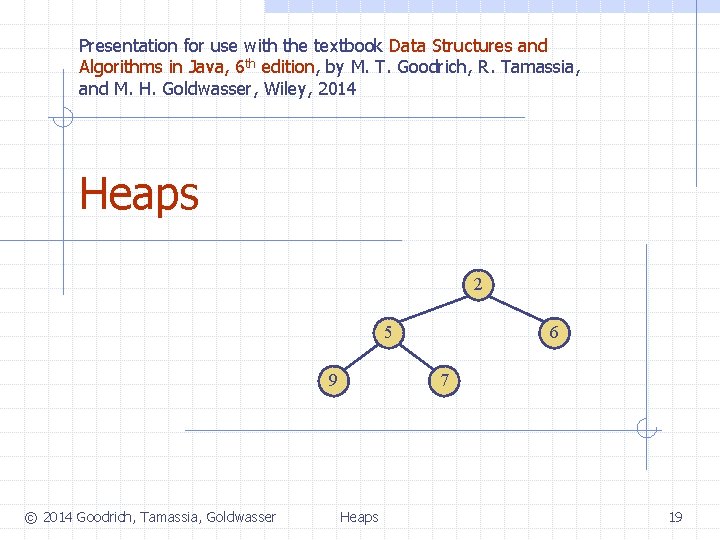
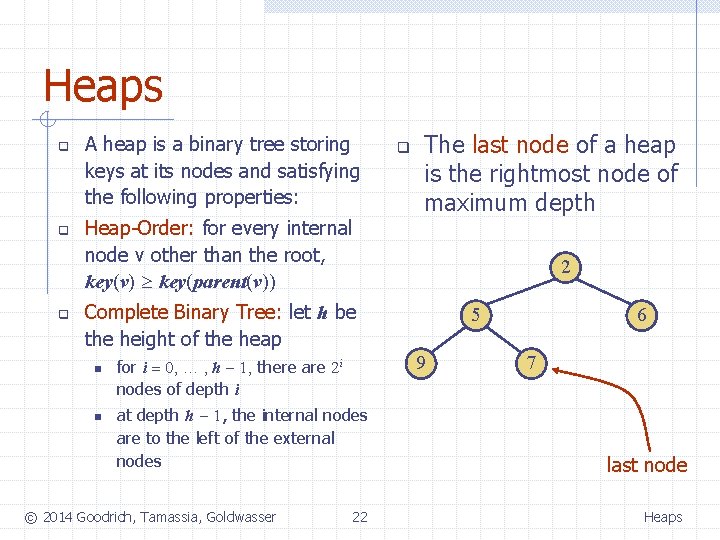
Heaps q q q A heap is a binary tree storing keys at its nodes and satisfying the following properties: Heap-Order: for every internal node v other than the root, key(v) key(parent(v)) q The last node of a heap is the rightmost node of maximum depth 2 Complete Binary Tree: let h be the height of the heap n n 9 for i = 0, … , h - 1, there are 2 i nodes of depth i at depth h - 1, the internal nodes are to the left of the external nodes © 2014 Goodrich, Tamassia, Goldwasser 5 22 6 7 last node Heaps

Height of a Heap q Theorem: A heap storing n keys has height O(log n) Proof: (we apply the complete binary tree property) Let h be the height of a heap storing n keys Since there are 2 i keys at depth i = 0, … , h - 1 and at least one key at depth h, we have n 1 + 2 + 4 + … + 2 h-1 + 1 Thus, n 2 h , i. e. , h log n n depth keys 0 1 1 2 h-1 2 h-1 h 1 © 2014 Goodrich, Tamassia, Goldwasser 23 Heaps

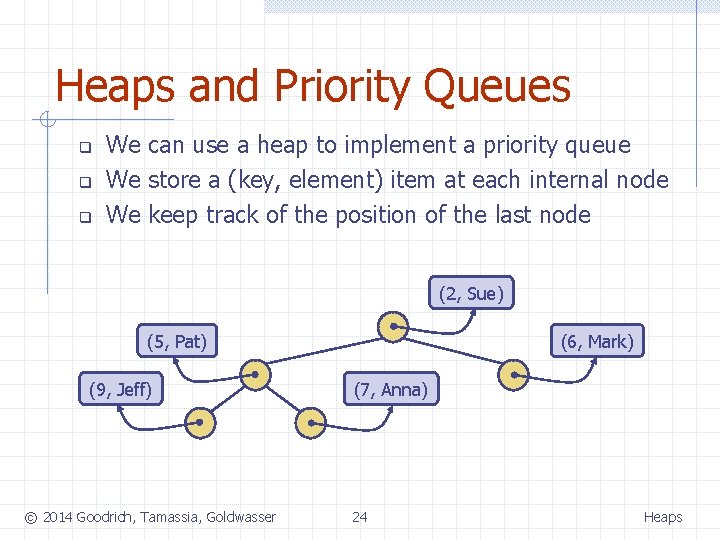
Heaps and Priority Queues q q q We can use a heap to implement a priority queue We store a (key, element) item at each internal node We keep track of the position of the last node (2, Sue) (5, Pat) (9, Jeff) © 2014 Goodrich, Tamassia, Goldwasser (6, Mark) (7, Anna) 24 Heaps

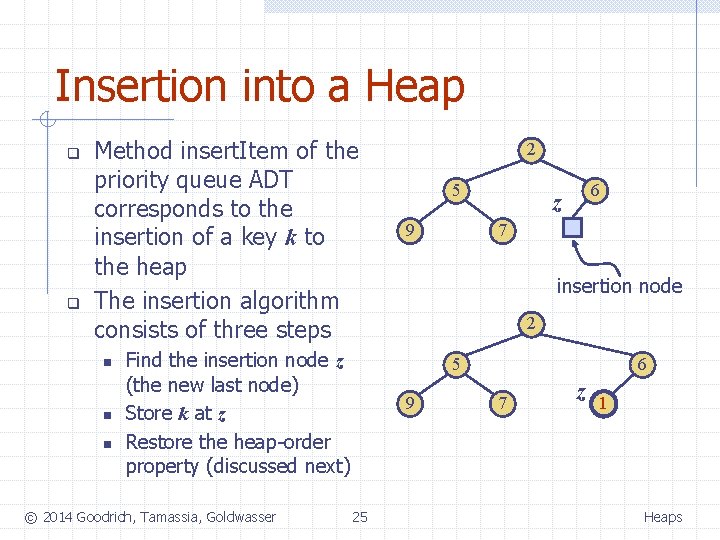
Insertion into a Heap q q Method insert. Item of the priority queue ADT corresponds to the insertion of a key k to the heap The insertion algorithm consists of three steps n n n Find the insertion node z (the new last node) Store k at z Restore the heap-order property (discussed next) © 2014 Goodrich, Tamassia, Goldwasser 2 5 9 6 z 7 insertion node 2 5 9 25 6 7 z 1 Heaps

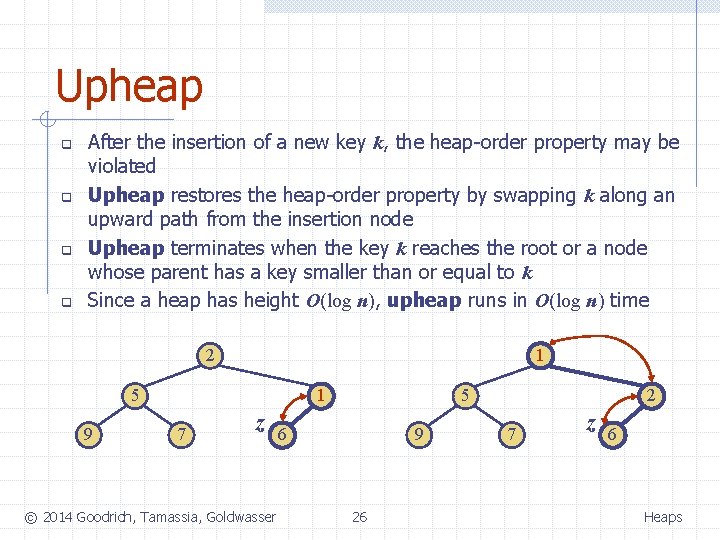
Upheap q q After the insertion of a new key k, the heap-order property may be violated Upheap restores the heap-order property by swapping k along an upward path from the insertion node Upheap terminates when the key k reaches the root or a node whose parent has a key smaller than or equal to k Since a heap has height O(log n), upheap runs in O(log n) time 2 1 5 9 1 7 z © 2014 Goodrich, Tamassia, Goldwasser 5 6 9 26 2 7 z 6 Heaps

Removal from a Heap q q Method remove. Min of the priority queue ADT corresponds to the removal of the root key from the heap The removal algorithm consists of three steps n n n 2 5 9 7 w last node 7 Replace the root key with the key of the last node w Remove w Restore the heap-order property (discussed next) © 2014 Goodrich, Tamassia, Goldwasser 6 5 w 6 9 new last node 27 Heaps

Downheap q q After replacing the root key with the key k of the last node, the heap-order property may be violated Downheap restores the heap-order property by swapping key k along a downward path from the root Downheap terminates when key k reaches a leaf or a node whose children have keys greater than or equal to k Since a heap has height O(log n), downheap runs in O(log n) time 7 5 w 5 6 7 9 © 2014 Goodrich, Tamassia, Goldwasser w 6 9 28 Heaps

Updating the Last Node q The insertion node can be found by traversing a path of O(log n) nodes n n n q Go up until a left child or the root is reached If a left child is reached, go to the right child Go down left until a leaf is reached Similar algorithm for updating the last node after a removal © 2014 Goodrich, Tamassia, Goldwasser 29 Heaps

Heap-Sort q Consider a priority queue with n items implemented by means of a heap n n n q the space used is O(n) methods insert and remove. Min take O(log n) time methods size, is. Empty, and min take time O(1) time © 2014 Goodrich, Tamassia, Goldwasser q q 30 Using a heap-based priority queue, we can sort a sequence of n elements in O(n log n) time The resulting algorithm is called heap-sort Heap-sort is much faster than quadratic sorting algorithms, such as insertion-sort and selection-sort Heaps

Array-based Heap Implementation q q We can represent a heap with n keys by means of an array of length n For the node at rank i n n q q the left child is at rank 2 i + 1 the right child is at rank 2 i + 2 Links between nodes are not explicitly stored Operation add corresponds to inserting at rank n + 1 Operation remove_min corresponds to removing at rank n Yields in-place heap-sort © 2014 Goodrich, Tamassia, Goldwasser 31 2 5 6 9 7 0 1 2 3 4 Heaps

Java Implementation © 2014 Goodrich, Tamassia, Goldwasser 32 Heaps

Java Implementation, 2 © 2014 Goodrich, Tamassia, Goldwasser 33 Heaps

Java Implementation, 3 © 2014 Goodrich, Tamassia, Goldwasser 34 Heaps

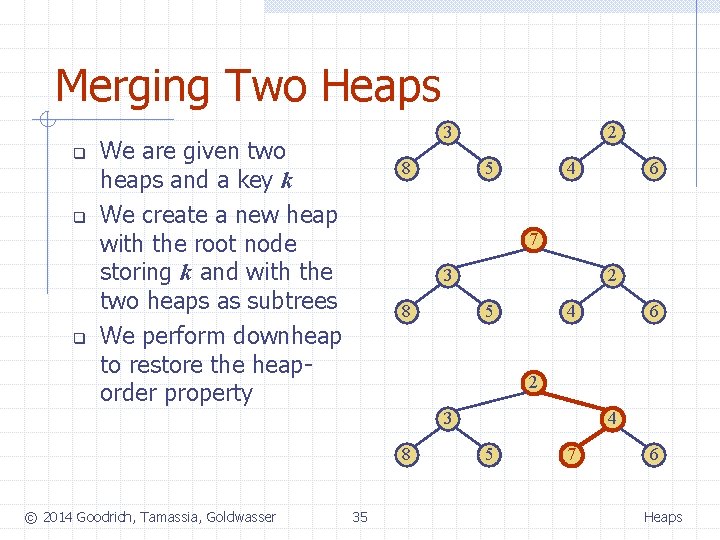
Merging Two Heaps q q q 3 We are given two heaps and a key k We create a new heap with the root node storing k and with the two heaps as subtrees We perform downheap to restore the heaporder property 8 2 5 4 7 3 8 2 5 4 6 2 3 8 © 2014 Goodrich, Tamassia, Goldwasser 6 35 4 5 7 6 Heaps

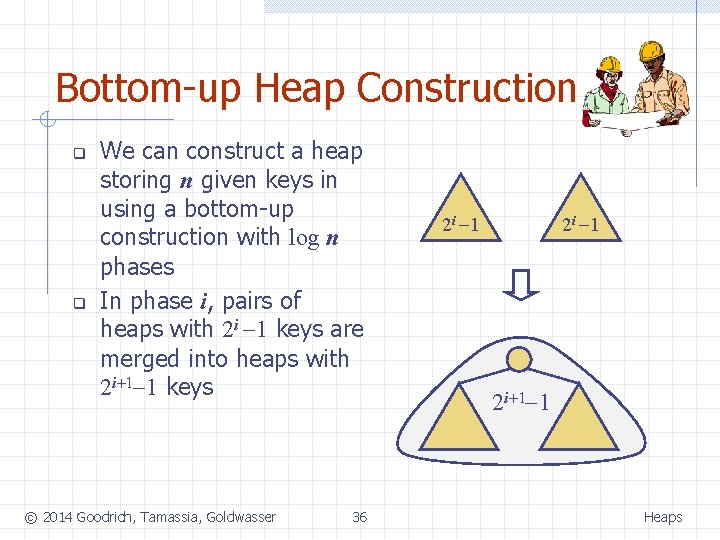
Bottom-up Heap Construction q q We can construct a heap storing n given keys in using a bottom-up construction with log n phases In phase i, pairs of heaps with 2 i -1 keys are merged into heaps with 2 i+1 -1 keys © 2014 Goodrich, Tamassia, Goldwasser 36 2 i -1 2 i+1 -1 Heaps

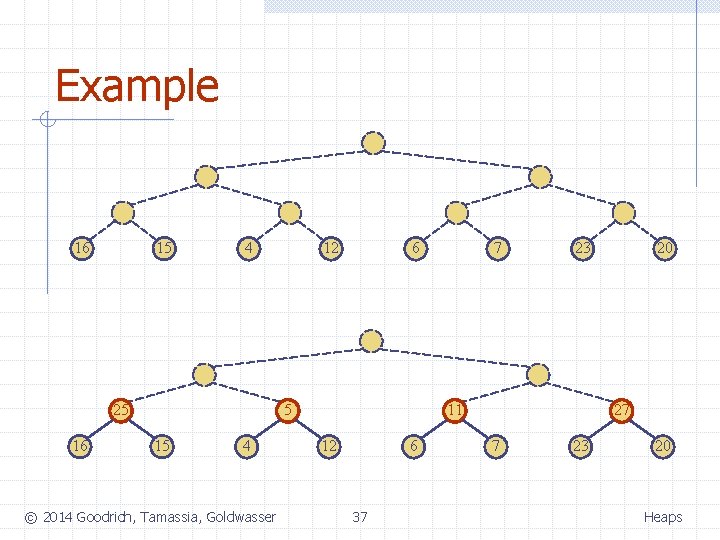
Example 16 15 4 25 16 12 6 5 15 4 © 2014 Goodrich, Tamassia, Goldwasser 7 23 11 12 6 37 20 27 7 23 20 Heaps

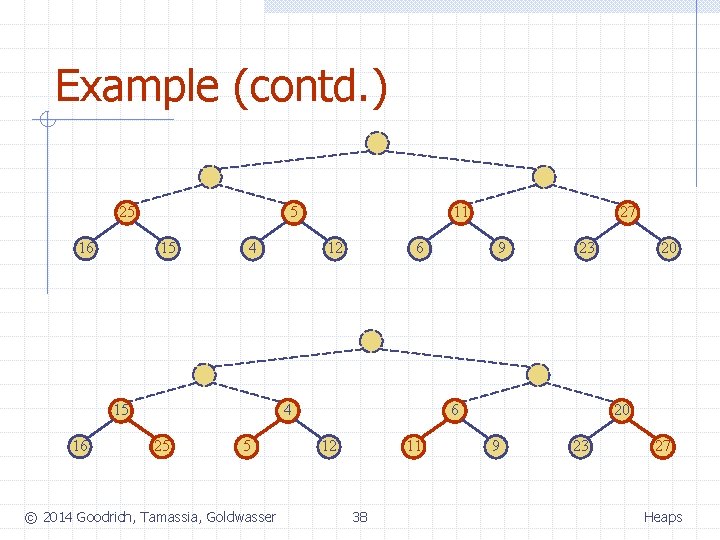
Example (contd. ) 25 16 5 15 4 15 16 11 12 6 4 25 5 © 2014 Goodrich, Tamassia, Goldwasser 27 9 23 6 12 11 38 20 20 9 23 27 Heaps

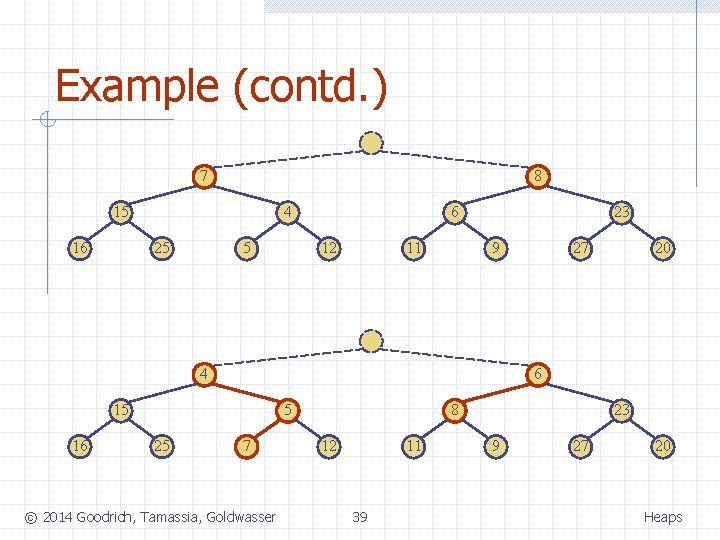
Example (contd. ) 7 8 15 16 4 25 5 6 12 11 23 9 4 5 25 20 6 15 16 27 7 © 2014 Goodrich, Tamassia, Goldwasser 8 12 11 39 23 9 27 20 Heaps

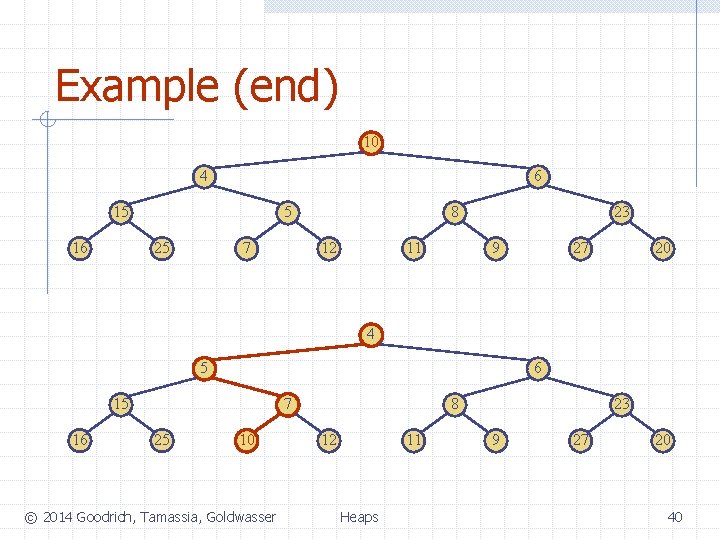
Example (end) 10 4 6 15 16 5 25 7 8 12 11 23 9 27 20 4 5 6 15 16 7 25 10 © 2014 Goodrich, Tamassia, Goldwasser 8 12 11 Heaps 23 9 27 20 40

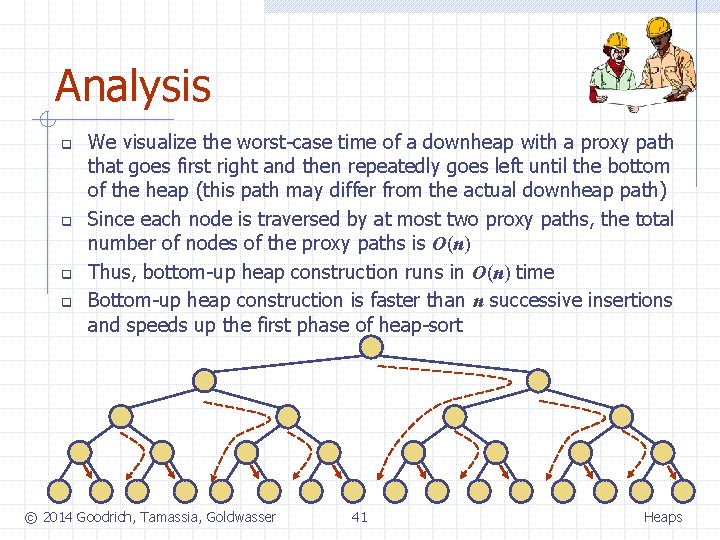
Analysis q q We visualize the worst-case time of a downheap with a proxy path that goes first right and then repeatedly goes left until the bottom of the heap (this path may differ from the actual downheap path) Since each node is traversed by at most two proxy paths, the total number of nodes of the proxy paths is O(n) Thus, bottom-up heap construction runs in O(n) time Bottom-up heap construction is faster than n successive insertions and speeds up the first phase of heap-sort © 2014 Goodrich, Tamassia, Goldwasser 41 Heaps

java. util. Priority. Queue Class q Values are keys n q More about java. util. Map. Entry later Uses a heap O(n) © 2014 Goodrich, Tamassia, Goldwasser Priority Queues 42

Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Adaptable Priority Queues 3 a 5 g © 2014 Goodrich, Tamassia, Goldwasser 4 e Adaptable Priority Queues 43

Entry and Priority Queue ADTs q q An entry stores a (key, value) pair Entry ADT methods: n n get. Key(): returns the key associated with this entry get. Value(): returns the value paired with the key associated with this entry q Priority Queue ADT: n n 44 insert(k, x) inserts an entry with key k and value x remove. Min() removes and returns the entry with smallest key min() returns, but does not remove, an entry with smallest key size(), is. Empty()

Example q Online trading system where orders to purchase and sell a stock are stored in priority queues n n What if someone wishes to cancel their order before it executes? What if someone wishes to update the price (key) or number of shares (value) for their order? 45

Methods of the Adaptable Priority Queue ADT remove(e): Remove from P and return entry e. q replace. Key(e, k): Replace with k and return the key of entry e of P; an error condition occurs if k is invalid (that is, k cannot be compared with other keys). q replace. Value(e, v): Replace with v and return the value of entry e of P. q © 2014 Goodrich, Tamassia, Goldwasser 46 Adaptable Priority Queues

Example Operation insert(5, A) insert(3, B) insert(7, C) min() key(e 2) remove(e 1) replace. Key(e 2, 9) replace. Value(e 3, D) (7, D), (9, B) remove(e 2) © 2014 Goodrich, Tamassia, Goldwasser Output e 1 e 2 e 3 e 2 3 e 1 3 C (5, A) (3, B), (5, A), (7, C) (3, B), (7, C), (9, B) e 2 (7, D) 47 P Adaptable Priority Queues

Locating Entries In order to implement the operations remove(e), replace. Key(e, k), and replace. Value(e, v), we need fast ways of locating an entry e in a priority queue. q We can always just search the entire data structure to find an entry e, but there are better ways for locating entries. q © 2014 Goodrich, Tamassia, Goldwasser 48 Adaptable Priority Queues

Location-Aware Entries q q A location-aware entry identifies and tracks the location of its (key, value) object within a data structure Intuitive notion: n q Reservation number Main idea: n Since entries are created and returned from the data structure itself, it can return location-aware entries, thereby making future updates easier © 2014 Goodrich, Tamassia, Goldwasser 49 Adaptable Priority Queues

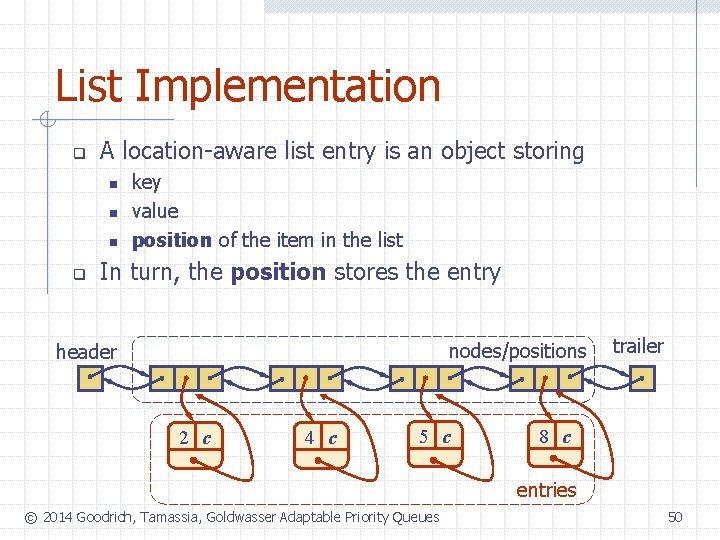
List Implementation q A location-aware list entry is an object storing n n n q key value position of the item in the list In turn, the position stores the entry nodes/positions header 2 c 4 c 5 c trailer 8 c entries © 2014 Goodrich, Tamassia, Goldwasser Adaptable Priority Queues 50

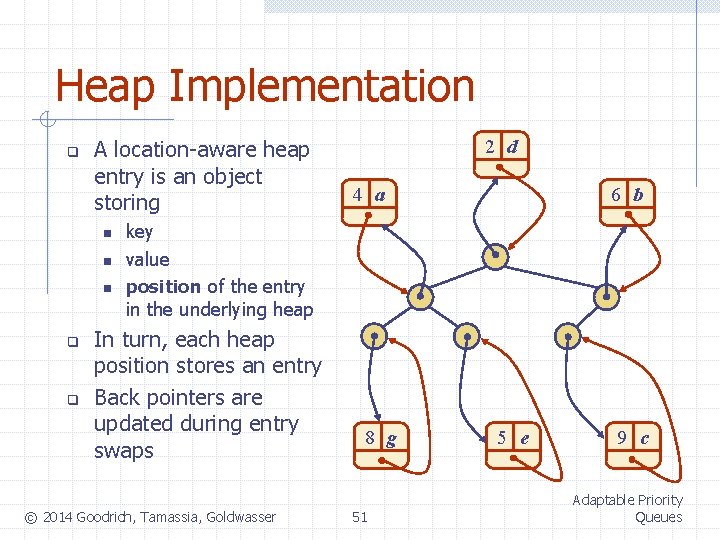
Heap Implementation q A location-aware heap entry is an object storing n n n q q 2 d 4 a 6 b key value position of the entry in the underlying heap In turn, each heap position stores an entry Back pointers are updated during entry swaps © 2014 Goodrich, Tamassia, Goldwasser 8 g 51 5 e 9 c Adaptable Priority Queues

Performance q Improved times thanks to location-aware entries are highlighted in red Method Unsorted List size, is. Empty O(1) insert O(1) min O(n) remove. Min O(n) remove O(1) replace. Key O(1) replace. Value O(1) © 2014 Goodrich, Tamassia, Goldwasser 52 Sorted List O(1) O(n) O(1) Heap O(1) O(log n) O(1) Adaptable Priority Queues

Java Implementation © 2014 Goodrich, Tamassia, Goldwasser 53 Adaptable Priority Queues

Java Implementation, 2 © 2014 Goodrich, Tamassia, Goldwasser 54 Adaptable Priority Queues

Java Implementation, 3 © 2014 Goodrich, Tamassia, Goldwasser 55 Adaptable Priority Queues

Java Implementation, 4 © 2014 Goodrich, Tamassia, Goldwasser 56 Adaptable Priority Queues

Reading • [G] Chapter 9 • [L] Section 6. 4 • Watch Course_Part_4 57