Graphs 337 LAX 2014 Goodrich Tamassia Goldwasser Graphs










- Slides: 17

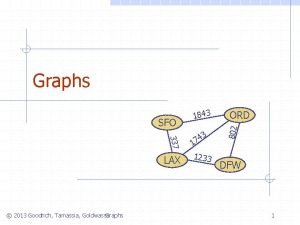
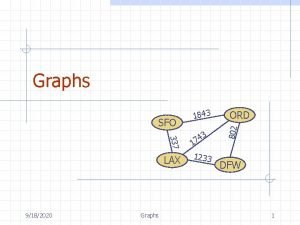
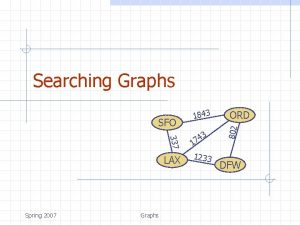
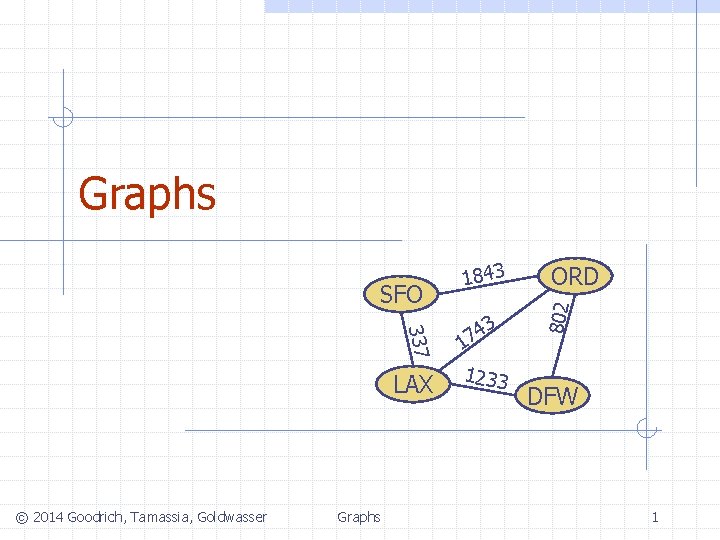
Graphs 337 LAX © 2014 Goodrich, Tamassia, Goldwasser Graphs 3 4 7 1 1233 ORD 802 SFO 1843 DFW 1

Graphs A graph is a pair (V, E), where n n n q V is a set of nodes, called vertices E is a collection of pairs of vertices, called edges Vertices and edges are positions and store elements Example: n n A vertex represents an airport and stores the three-letter airport code An edge represents a flight route between two airports and stores the mileage of the route SFO 337 HNL 2555 LAX © 2014 Goodrich, Tamassia, Goldwasser 1843 3 4 17 1233 849 ORD 802 q DFW Graphs 2 PVD 14 7 8 3 1 LGA 1120 10 99 MIA 2

Edge Types q Directed edge n n q n unordered pair of vertices (u, v) e. g. , a flight route Directed graph n n q ORD flight AA 1206 PVD ORD 849 miles PVD Undirected edge n q ordered pair of vertices (u, v) first vertex u is the origin second vertex v is the destination e. g. , a flight all the edges are directed e. g. , flight network Undirected graph n n all the edges are undirected e. g. , route network © 2014 Goodrich, Tamassia, Goldwasser Graphs 3

Applications q Electronic circuits n n q Transportation networks n n q Highway network Flight network Computer networks n n n q Printed circuit board Integrated circuit Local area network Internet Web Databases n Entity-relationship diagram © 2014 Goodrich, Tamassia, Goldwasser Graphs 4

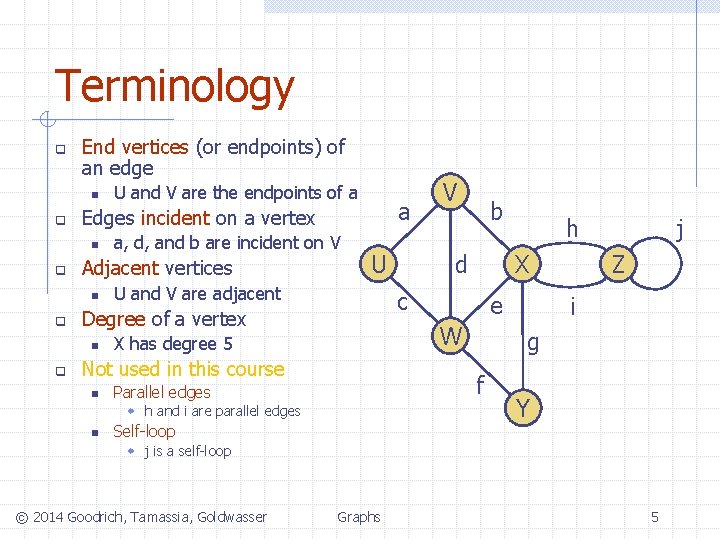
Terminology q End vertices (or endpoints) of an edge n q U U and V are adjacent Self-loop h X d e j Z i g f Parallel edges w h and i are parallel edges n b W X has degree 5 Not used in this course n V c Degree of a vertex n q a, d, and b are incident on V Adjacent vertices n q a Edges incident on a vertex n q U and V are the endpoints of a Y w j is a self-loop © 2014 Goodrich, Tamassia, Goldwasser Graphs 5

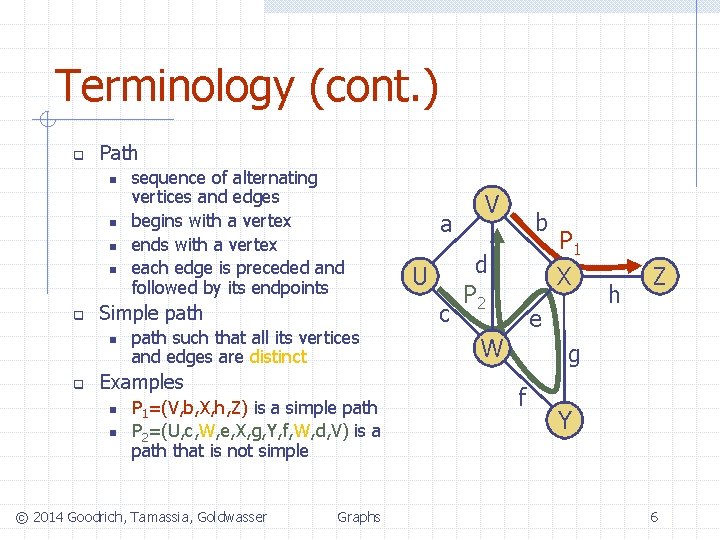
Terminology (cont. ) q Path n n q Simple path n q sequence of alternating vertices and edges begins with a vertex ends with a vertex each edge is preceded and followed by its endpoints path such that all its vertices and edges are distinct Examples n n P 1=(V, b, X, h, Z) is a simple path P 2=(U, c, W, e, X, g, Y, f, W, d, V) is a path that is not simple © 2014 Goodrich, Tamassia, Goldwasser Graphs a U c V b d P 2 P 1 X e W h Z g f Y 6

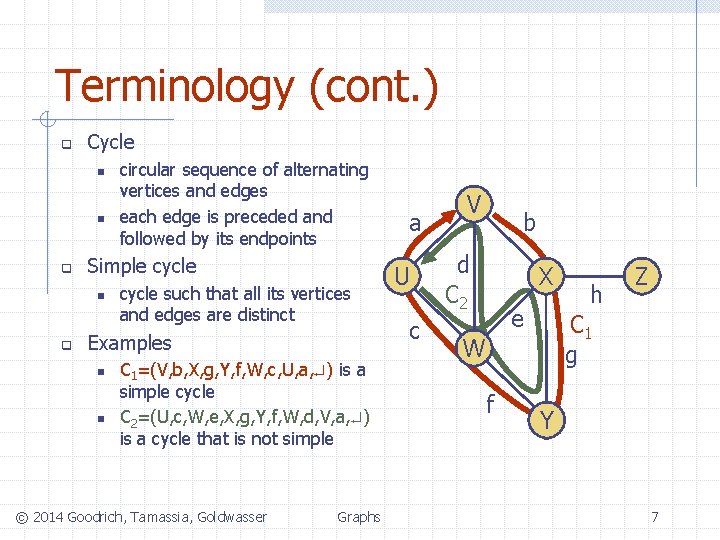
Terminology (cont. ) q Cycle n n q Simple cycle n q circular sequence of alternating vertices and edges each edge is preceded and followed by its endpoints cycle such that all its vertices and edges are distinct Examples n n C 1=(V, b, X, g, Y, f, W, c, U, a, ) is a simple cycle C 2=(U, c, W, e, X, g, Y, f, W, d, V, a, ) is a cycle that is not simple © 2014 Goodrich, Tamassia, Goldwasser Graphs a U c V b d C 2 X e C 1 g W f h Z Y 7

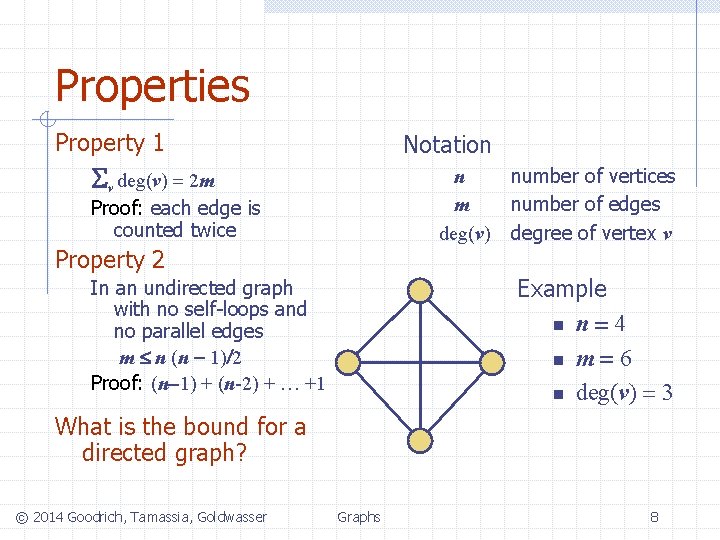
Properties Property 1 Notation Sv deg(v) = 2 m n m deg(v) Proof: each edge is counted twice Property 2 number of vertices number of edges degree of vertex v Example n n = 4 n m = 6 n deg(v) = 3 In an undirected graph with no self-loops and no parallel edges m n (n - 1)/2 Proof: (n-1) + (n-2) + … +1 What is the bound for a directed graph? © 2014 Goodrich, Tamassia, Goldwasser Graphs 8

Vertices and Edges q q A graph is a collection of vertices and edges. A Vertex n n q stores an arbitrary element provided by the user (e. g. , an airport code) We assume it supports a method, element(), to retrieve the stored element. An Edge n stores an associated object (e. g. , a flight number, travel distance, cost), retrieved with the element( ) method. © 2014 Goodrich, Tamassia, Goldwasser Graphs 9

Graph ADT q q q get. Adjacent. Vertices(v) n Given vertex v, return adjacent vertices are. Adjacent(u, v) n Are vertices u and v adjacent? … © 2014 Goodrich, Tamassia, Goldwasser Graphs 10

Representing a Graph Linked lists q Arrays q © 2014 Goodrich, Tamassia, Goldwasser Graphs 11

Adjacency Lists q for each vertex n n sequence of vertices Sequence of vertices with edge information v w u v z w © 2014 Goodrich, Tamassia, Goldwasser Graphs 12

Adjacency Matrix q q 2 D-array Content n n q Edge struct for edge Null for no edge Content n n 1 for edge 0 for no edge © 2014 Goodrich, Tamassia, Goldwasser Graphs 13

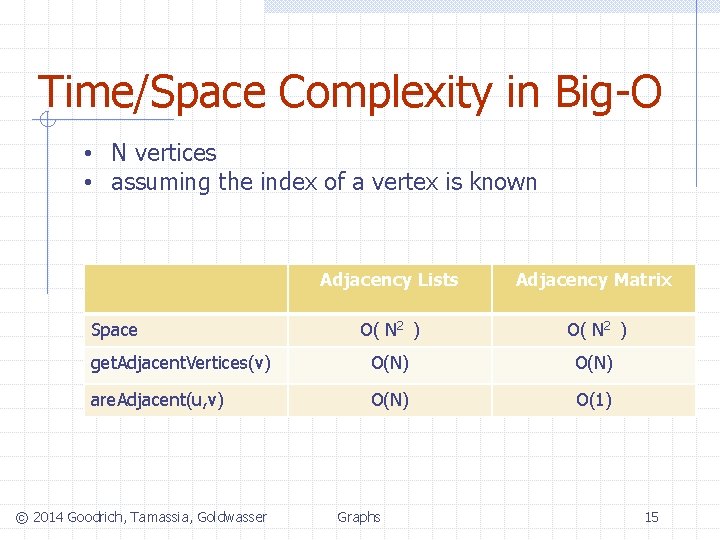
Time/Space Complexity in Big-O • N vertices • assuming the index of a vertex is known Adjacency Lists Adjacency Matrix Space get. Adjacent. Vertices(v) are. Adjacent(u, v) © 2014 Goodrich, Tamassia, Goldwasser Graphs 14

Time/Space Complexity in Big-O • N vertices • assuming the index of a vertex is known Adjacency Lists Adjacency Matrix O( N 2 ) get. Adjacent. Vertices(v) O(N) are. Adjacent(u, v) O(N) O(1) Space © 2014 Goodrich, Tamassia, Goldwasser Graphs 15

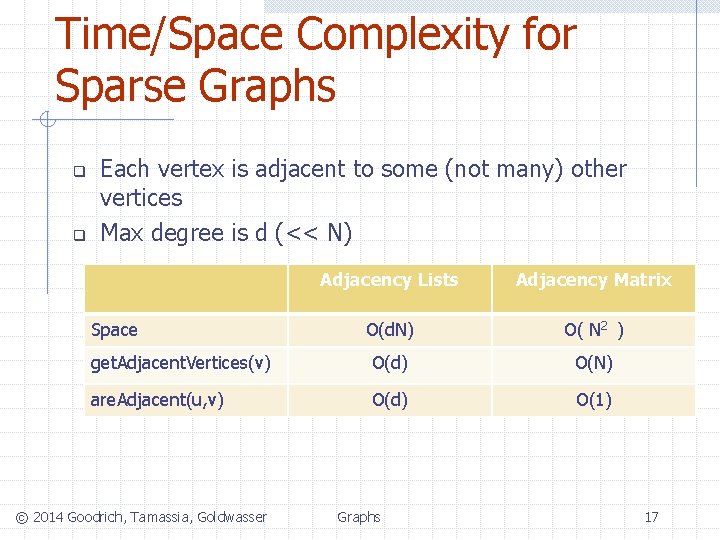
Time/Space Complexity for Sparse Graphs q q Each vertex is adjacent to some (not many) other vertices [e. g. Social network] Max degree is d (<< N) Adjacency Lists Adjacency Matrix Space get. Adjacent. Vertices(v) are. Adjacent(u, v) © 2014 Goodrich, Tamassia, Goldwasser Graphs 16

Time/Space Complexity for Sparse Graphs q q Each vertex is adjacent to some (not many) other vertices Max degree is d (<< N) Adjacency Lists Adjacency Matrix O(d. N) O( N 2 ) get. Adjacent. Vertices(v) O(d) O(N) are. Adjacent(u, v) O(d) O(1) Space © 2014 Goodrich, Tamassia, Goldwasser Graphs 17