Graphs 337 LAX 9182020 Graphs 3 4 7

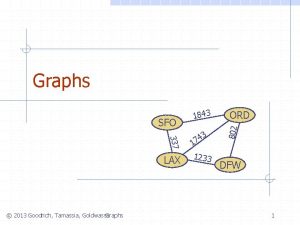
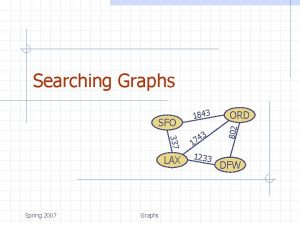
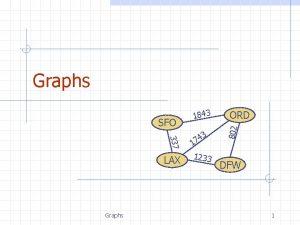
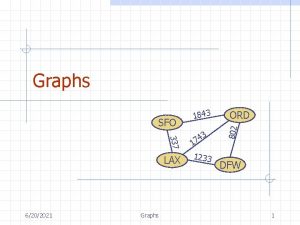
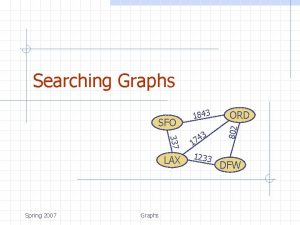
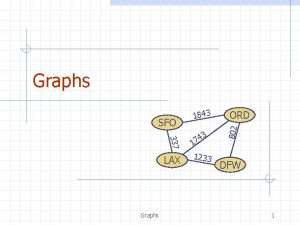
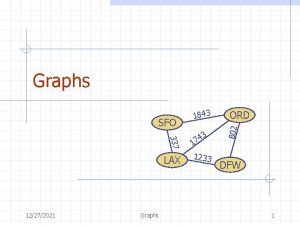
Graphs 337 LAX 9/18/2020 Graphs 3 4 7 1 1233 ORD 802 SFO 1843 DFW 1

Outline and Reading Graphs (§ 6. 1) n n n Definition Applications Terminology Properties ADT Data structures for graphs (§ 6. 2) n n n 9/18/2020 Edge list structure Adjacency matrix structure Graphs 2

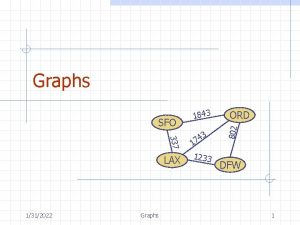
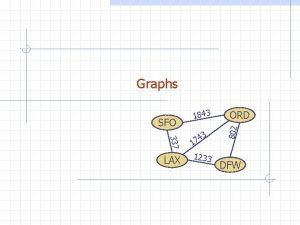
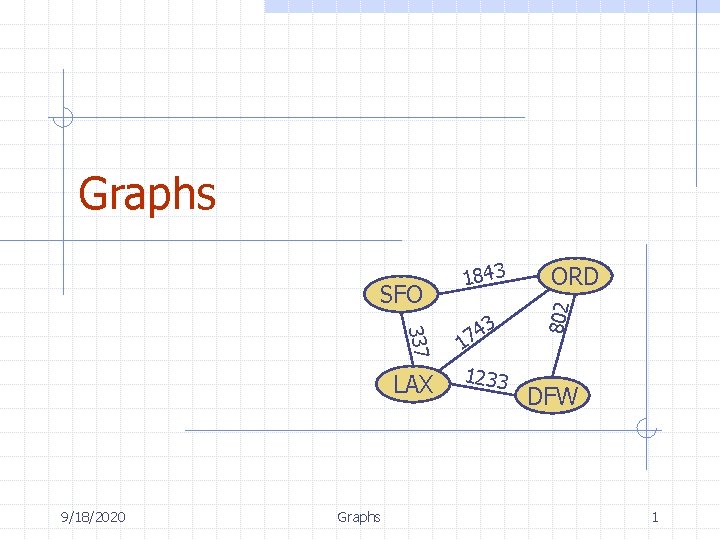
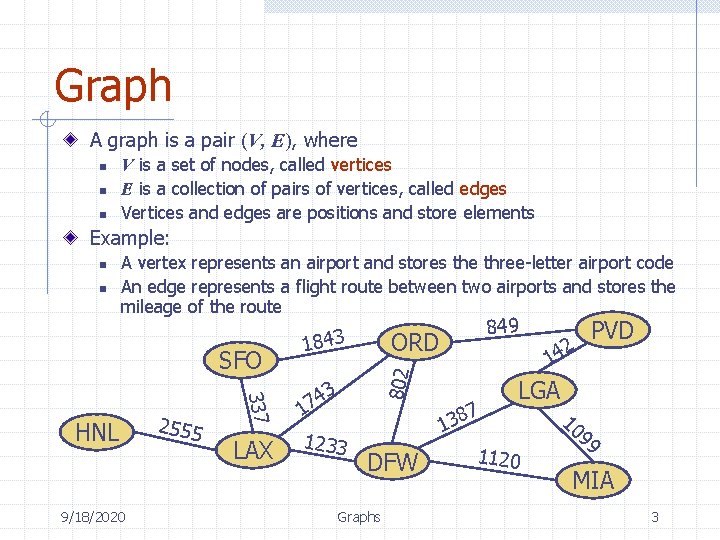
Graph A graph is a pair (V, E), where n n n V is a set of nodes, called vertices E is a collection of pairs of vertices, called edges Vertices and edges are positions and store elements Example: n A vertex represents an airport and stores the three-letter airport code An edge represents a flight route between two airports and stores the mileage of the route SFO 9/18/2020 337 HNL 2555 LAX 1843 3 4 17 1233 849 ORD 802 n DFW Graphs 2 PVD 14 7 8 3 1 LGA 1120 10 99 MIA 3

Edge Types Directed edge n n ordered pair of vertices (u, v) first vertex u is the origin second vertex v is the destination e. g. , a flight ORD flight AA 1206 PVD ORD 849 miles PVD Undirected edge n n unordered pair of vertices (u, v) e. g. , a flight route Directed graph n n all the edges are directed e. g. , route network Undirected graph n n all the edges are undirected e. g. , flight network 9/18/2020 Graphs 4

Applications Electronic circuits n n Printed circuit board Integrated circuit Transportation networks n n Highway network Flight network Computer networks n n n Local area network Internet Web Databases n Entity-relationship diagram 9/18/2020 Graphs 5

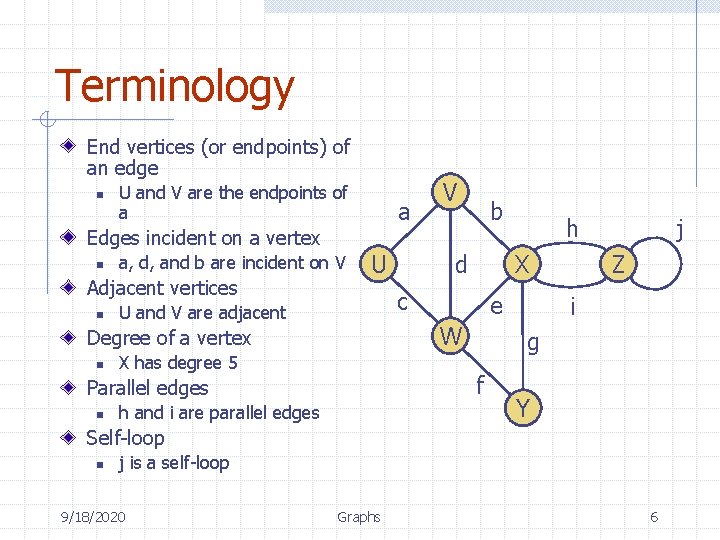
Terminology End vertices (or endpoints) of an edge n U and V are the endpoints of a a Edges incident on a vertex n a, d, and b are incident on V Adjacent vertices n e W X has degree 5 j Z i g f h and i are parallel edges h X c U and V are adjacent Parallel edges n b d U Degree of a vertex n V Y Self-loop n j is a self-loop 9/18/2020 Graphs 6

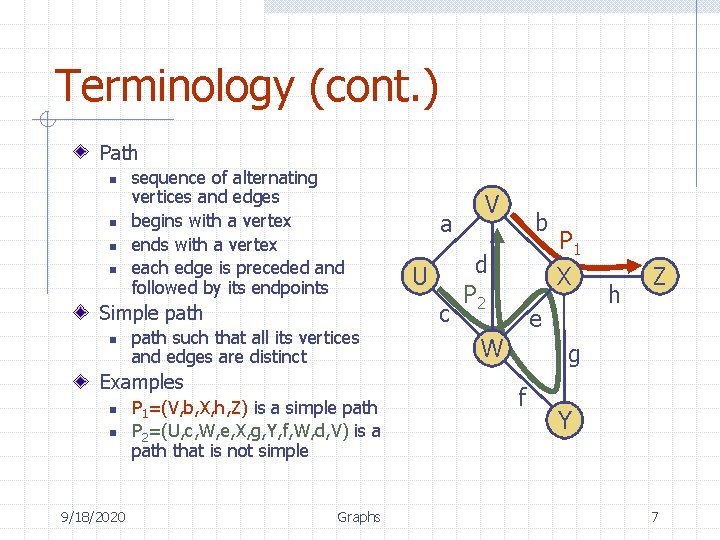
Terminology (cont. ) Path n n sequence of alternating vertices and edges begins with a vertex ends with a vertex each edge is preceded and followed by its endpoints Simple path n path such that all its vertices and edges are distinct Examples n n 9/18/2020 P 1=(V, b, X, h, Z) is a simple path P 2=(U, c, W, e, X, g, Y, f, W, d, V) is a path that is not simple Graphs a U c V b d P 2 P 1 X e W h Z g f Y 7

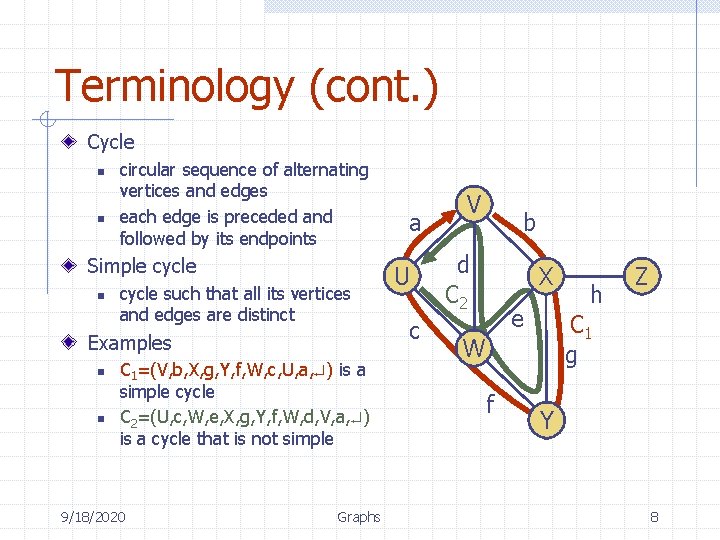
Terminology (cont. ) Cycle n n circular sequence of alternating vertices and edges each edge is preceded and followed by its endpoints Simple cycle n cycle such that all its vertices and edges are distinct Examples n n C 1=(V, b, X, g, Y, f, W, c, U, a, ) is a simple cycle C 2=(U, c, W, e, X, g, Y, f, W, d, V, a, ) is a cycle that is not simple 9/18/2020 Graphs a U c V b d C 2 X e C 1 g W f h Z Y 8

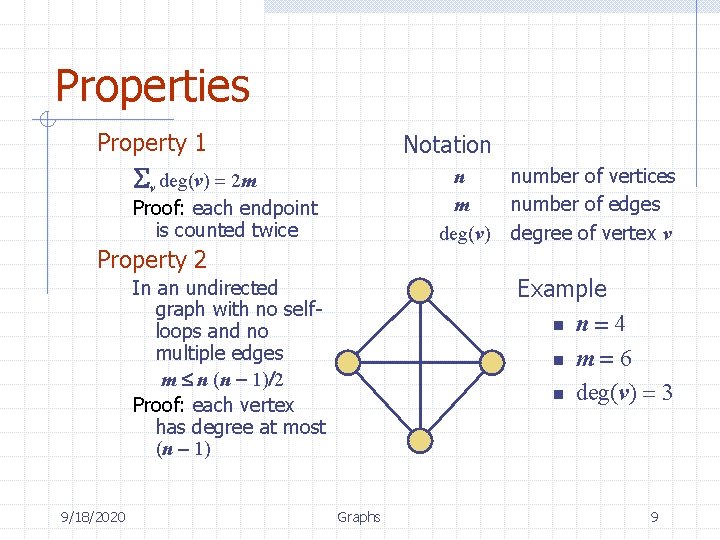
Properties Property 1 Notation Sv deg(v) = 2 m n m deg(v) Proof: each endpoint is counted twice Property 2 Example n n = 4 n m = 6 n deg(v) = 3 In an undirected graph with no selfloops and no multiple edges m n (n - 1)/2 Proof: each vertex has degree at most (n - 1) 9/18/2020 number of vertices number of edges degree of vertex v Graphs 9

Main Methods of the Graph ADT Vertices and edges n n Update methods are positions store elements n n Accessor methods n n n n 9/18/2020 n a. Vertex() incident. Edges(v) end. Vertices(e) is. Directed(e) origin(e) destination(e) opposite(v, e) are. Adjacent(v, w) n n insert. Vertex(o) insert. Edge(v, w, o) insert. Directed. Edge(v, w, o) remove. Vertex(v) remove. Edge(e) Generic methods n n Graphs num. Vertices() num. Edges() vertices() edges() 10

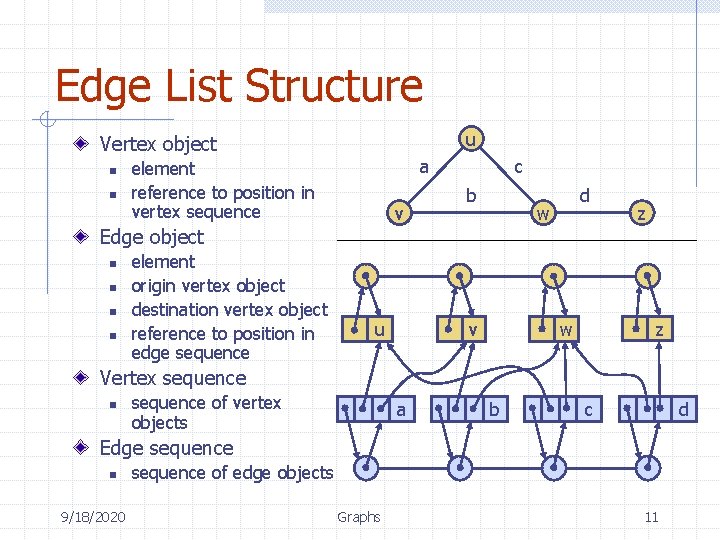
Edge List Structure u Vertex object n n a element reference to position in vertex sequence v c b d w z Edge object n n element origin vertex object destination vertex object reference to position in edge sequence u z w v Vertex sequence n sequence of vertex objects a b c d Edge sequence n 9/18/2020 sequence of edge objects Graphs 11

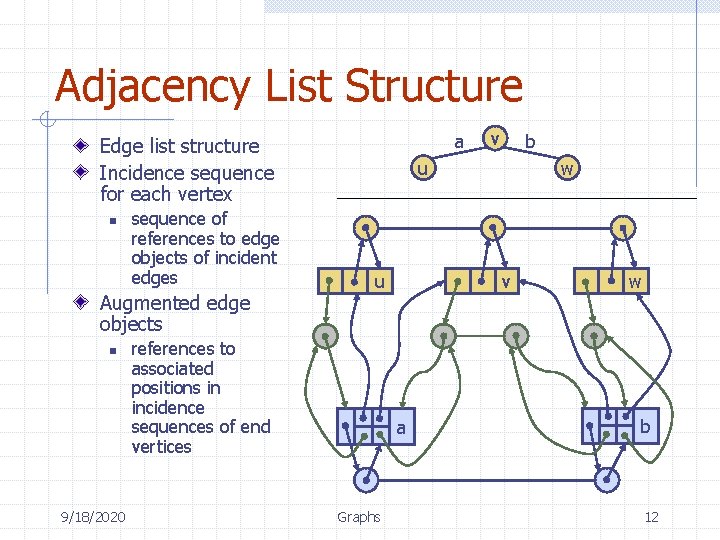
Adjacency List Structure a Edge list structure Incidence sequence for each vertex n sequence of references to edge objects of incident edges Augmented edge objects n 9/18/2020 v b u u references to associated positions in incidence sequences of end vertices v a Graphs w w b 12

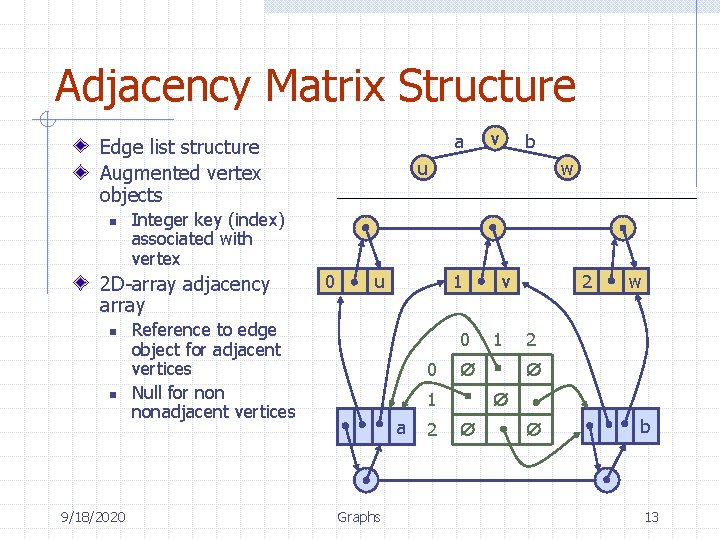
Adjacency Matrix Structure a Edge list structure Augmented vertex objects n n 9/18/2020 b u w Integer key (index) associated with vertex 2 D-array adjacency array n v 0 u Reference to edge object for adjacent vertices Null for nonadjacent vertices 1 0 0 Graphs 2 1 w 2 1 a 2 v b 13

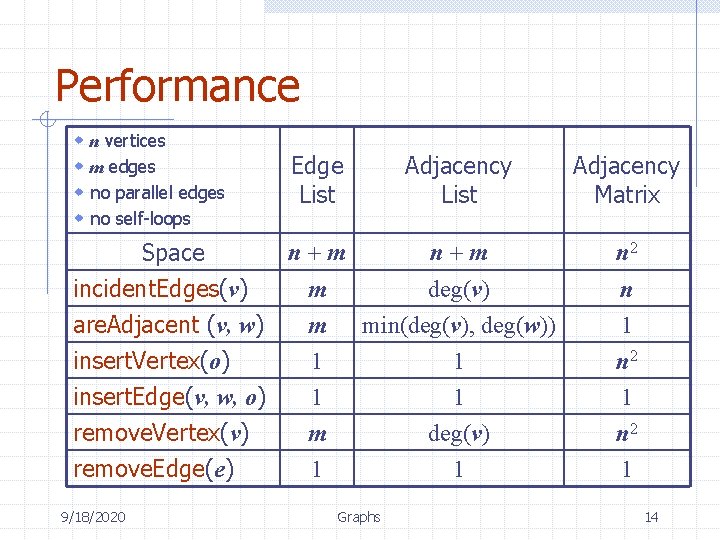
Performance w n vertices w m edges w no parallel edges w no self-loops Edge List Adjacency Matrix Space incident. Edges(v) are. Adjacent (v, w) insert. Vertex(o) n+m n 2 m m 1 deg(v) min(deg(v), deg(w)) 1 n 2 insert. Edge(v, w, o) 1 1 1 remove. Vertex(v) remove. Edge(e) m 1 deg(v) 1 n 2 1 9/18/2020 Graphs 14