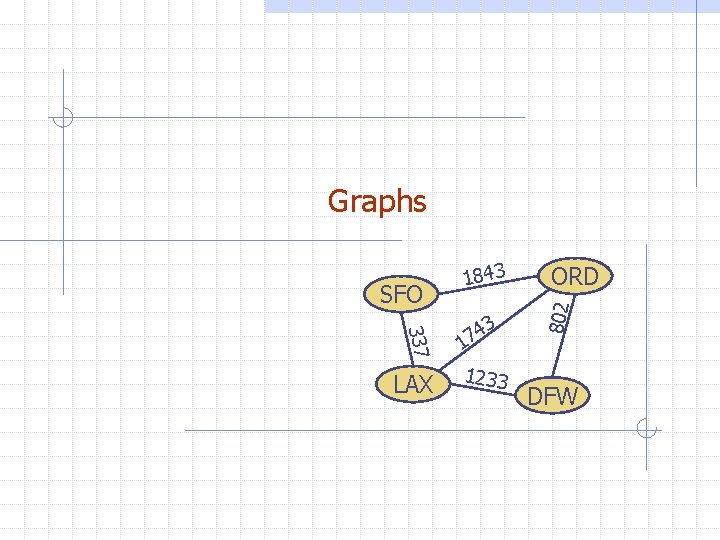
Graphs 337 LAX 3 4 7 1 1233

Graphs 337 LAX 3 4 7 1 1233 ORD 802 SFO 1843 DFW

Outline and Reading Graphs (§ 6. 1) n Definitions n Applications n Terminology n Properties n ADT Data structures for graphs (§ 6. 2) n Edge list structure n Adjacency matrix structure 2

Position ADT- Recall from Chpt 2 The Position ADT models the notion of the place within a data structure where a single object is stored It gives a unified view of diverse ways of storing data, such as n a cell of an array n a node of a linked list Just one method: n object element(): returns the element stored at the position 3

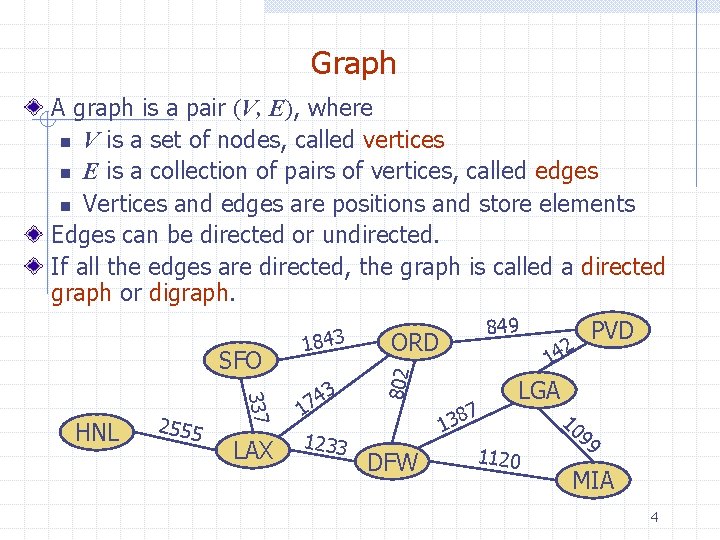
Graph A graph is a pair (V, E), where n V is a set of nodes, called vertices n E is a collection of pairs of vertices, called edges n Vertices and edges are positions and store elements Edges can be directed or undirected. If all the edges are directed, the graph is called a directed graph or digraph. 337 HNL 2555 LAX 3 4 17 1233 849 ORD 802 SFO 1843 DFW 2 PVD 14 7 8 3 1 LGA 1120 10 99 MIA 4

Examples of Graphs Airline route map n n Vertices: an airport identified by a three-letter airport code Edges: a flight route between two airports and specified by the mileage of the route Flowcharts n n n These represent the flow of control in a procedure. Vertices: symbolic flowchart boxes and diamonds Edges: connecting lines Binary relations n n n We say x. Ry if (x, y) ε Sx. S, where S is a set. Vertices: elements in S Edges: connect x and y iff x. Ry. 5

Examples of Graphs Computer networks n Vertices: computers n Edges: communication links Electric circuits n Vertices: diodes, transistors, capacitors, switches, . . . n Edges: Connecting wires These examples suggest the type of questions that can be asked when working with graphs: n n n What is the cheapest way to fly to NY What route involves the least flying time? If one city is closed due to bad weather, does a route to NY exist? 6

Edge Types Directed edge n ordered pair of vertices (u, v) n first vertex u is the origin n second vertex v is the destination n e. g. , a flight Undirected edge n unordered pair of vertices (u, v) n e. g. , a flight route Directed graph n all the edges are directed n e. g. , flight network Undirected graph n all the edges are undirected n e. g. , route network ORD flight AA 1206 PVD ORD 849 miles PVD 7

Applications Electronic circuits n n Printed circuit board Integrated circuit Transportation networks n n Highway network Flight network Computer networks n n n Local area network Internet Web Databases n Entity-relationship diagram 8

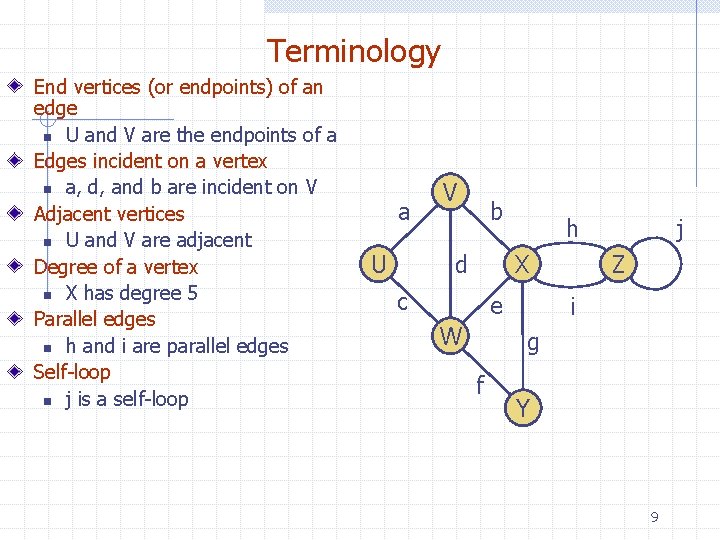
Terminology End vertices (or endpoints) of an edge n U and V are the endpoints of a Edges incident on a vertex n a, d, and b are incident on V Adjacent vertices n U and V are adjacent Degree of a vertex n X has degree 5 Parallel edges n h and i are parallel edges Self-loop n j is a self-loop a V b d U h X c e W j Z i g f Y 9

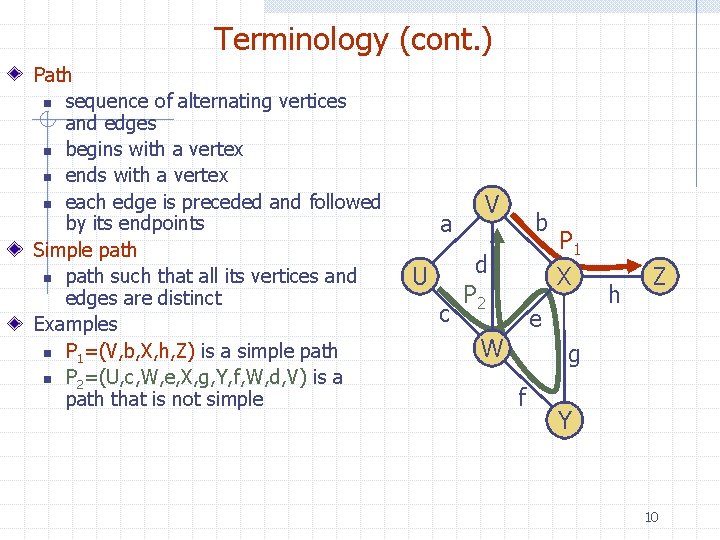
Terminology (cont. ) Path n sequence of alternating vertices and edges n begins with a vertex n ends with a vertex n each edge is preceded and followed by its endpoints Simple path n path such that all its vertices and edges are distinct Examples n P 1=(V, b, X, h, Z) is a simple path n P 2=(U, c, W, e, X, g, Y, f, W, d, V) is a path that is not simple a U c V b d P 2 P 1 X e W h Z g f Y 10

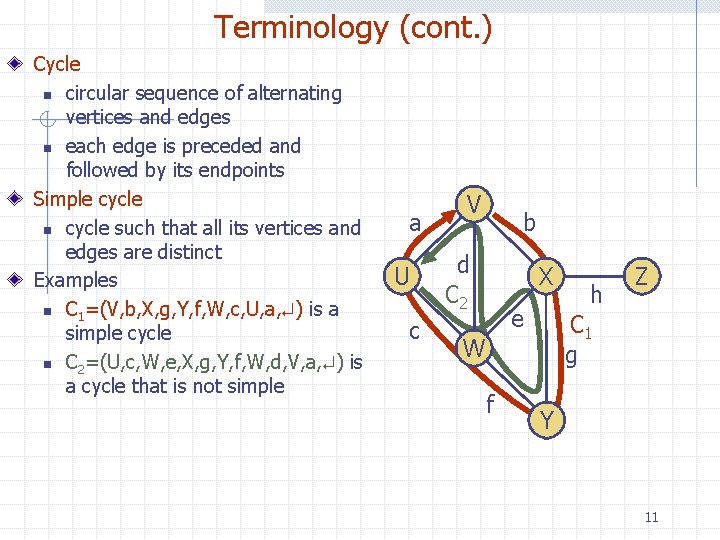
Terminology (cont. ) Cycle n circular sequence of alternating vertices and edges n each edge is preceded and followed by its endpoints Simple cycle n cycle such that all its vertices and edges are distinct Examples n C 1=(V, b, X, g, Y, f, W, c, U, a, ) is a simple cycle n C 2=(U, c, W, e, X, g, Y, f, W, d, V, a, ) is a cycle that is not simple a U c V b d C 2 X e C 1 g W f h Z Y 11

Properties Property 1 Sv deg(v) = 2 m Proof: each edge is counted twice Property 2 In an undirected graph with no selfloops and no multiple edges (i. e. a simple graph) m n (n - 1)/2 Proof: No 2 edges can have the same endpoints. Thus, each vertex has degree at most (n -1). Thus, by above, 2 m≤n(n-1) What is the bound for a directed graph? Notation n m deg(v) number of vertices number of edges degree of vertex v Example n n = 4 n m = 6 n deg(v) = 3 m≤n(n-1) Proof: No edge can have the same origin and destination. 12

Iterator ADT- Recall from Chpt 2 An iterator abstracts the process of scanning through a collection of elements Methods of the Object. Iterator ADT: n object() n boolean has. Next() n object next. Object() n reset() Extends the concept of Position by adding a traversal capability Implement with an array or singly linked list An iterator is typically associated with an another data structure We can augment the Stack, Queue, Vector, List and Sequence ADTs with method: n Object. Iterator elements() Two notions of iterator: n snapshot: freezes the contents of the data structure at a given time n dynamic: follows changes to the data structure 13

Main Methods of the Graph ADT v=vertex & e=edge n are positions n store elements (o) Update methods n insert. Vertex(o) n insert. Edge(v, w, o) n insert. Directed. Edge(v, w, o) n remove. Vertex(v) n remove. Edge(e) n make. Undirected(e) n reverse. Direction(e) n set. Direction. From(e, v) n set. Direction. To(e, v) Generic methods n num. Vertices() n num. Edges() n vertices() n edges() See pages 294 and 295 for definitions, although most are obvious. Color key: Returns an iterator Boolean 14

Main Methods of the Graph ADT Accessor methods a. Vertex() - returns any vertex as a graph may not have a special vertex n incident. Edges(v) n adjacent. Edges(v) n end. Vertices(e) n opposite(v, e) n are. Adjacent(v, w) n degree(v) See pages 294 and 295 for definitions, although most are obvious. Color key: Returns an iterator Boolean n Needed for graphs with directed edges n directed. Edges() n undirected. Edges() n origin(e) n destination(e) n is. Directed(e) Relating methods n in. Degree(v) n out. Degree(v) n in. Incident. Edges(v) n out. Incident. Edges(v) n in. Adjacent. Vertices(v) n out. Adjacent. Vertices(v) 15

Why are there so many methods for graphs? Graphs are very rich and versatile structures. Therefore, the number of methods is unavoidable when describing the needed methods. Realize that graphs support two kinds of positions - vertices and edges. Moreover, edges can be directed or undirected. Consequently, we need different methods for accessing and updating all these different positions as well as handling relationships between the different positions. 16

Data Structures for Graphs Most commonly used n Edge list structure n Adjacency matrix structure Each has its own strengths and weaknesses in terms of what methods are easier to use and the cost of storage space. The edge list and the adjacency list actually store representations of the edges. The adjacency matrix format only uses a placeholder for every pair of vertices. This implies, as we will see, that the list structures use O(n+m) space and matrix format uses O(n 2) where n is number of vertices and m is number of edges. 17

Sequence ADT Recall from Chpt 2 The Sequence ADT is the union of the Vector and List ADTs Elements accessed by n n List-based methods: n Rank, or Position Generic methods: n size(), is. Empty() Vector-based methods: n elem. At. Rank(r), replace. At. Rank(r, o), insert. At. Rank(r, o), remove. At. Rank(r) first(), last(), before(p), after(p), replace. Element(p, o), swap. Elements(p, q), insert. Before(p, o), insert. After(p, o), insert. First(o), insert. Last(o), remove(p) Bridge methods: n at. Rank(r), rank. Of(p) 18

Applications of Sequences The Sequence ADT is a basic, general-purpose, data structure for storing an ordered collection of elements Direct applications: n n Generic replacement for stack, queue, vector, or list small database (e. g. , address book) Indirect applications: n Building block of more complex data structures 19

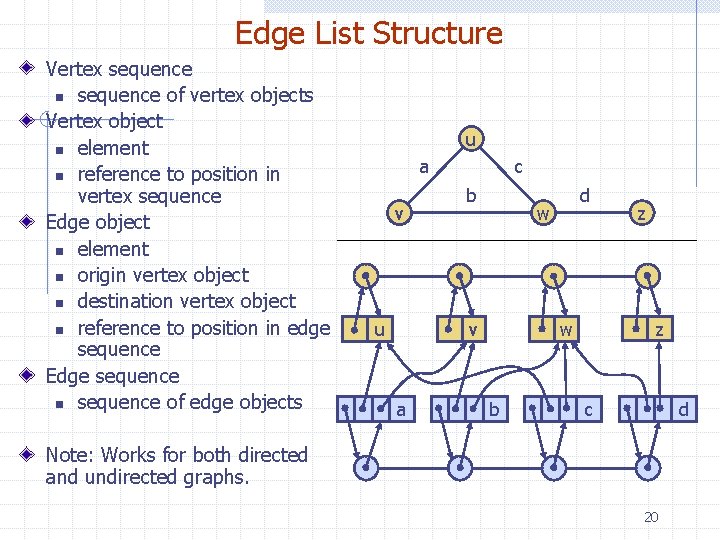
Edge List Structure Vertex sequence n sequence of vertex objects Vertex object n element n reference to position in vertex sequence Edge object n element n origin vertex object n destination vertex object n reference to position in edge sequence Edge sequence n sequence of edge objects u a v u c b w b z z w v a d c d Note: Works for both directed and undirected graphs. 20

Edge List Structure - Notes This is the simplest and most used data structure for a graph. The vertex and edge sequence could be a list, vector, or dictionary. If we use a vector representation, we could think of the vertices as being numbered. Vertex and edge objects may contain additional information, especially for graphs with some directed edges i, e, an edge vertex could have a Boolean variable indicating whether or not it was directed. Main feature: Provides direct access from edges to the vertices to which they are incident. But, accessing the edges that are incident on a vertex requires that all edges be examined. Obviously, performance of the various methods is very dependent upon which representation is chosen. 21

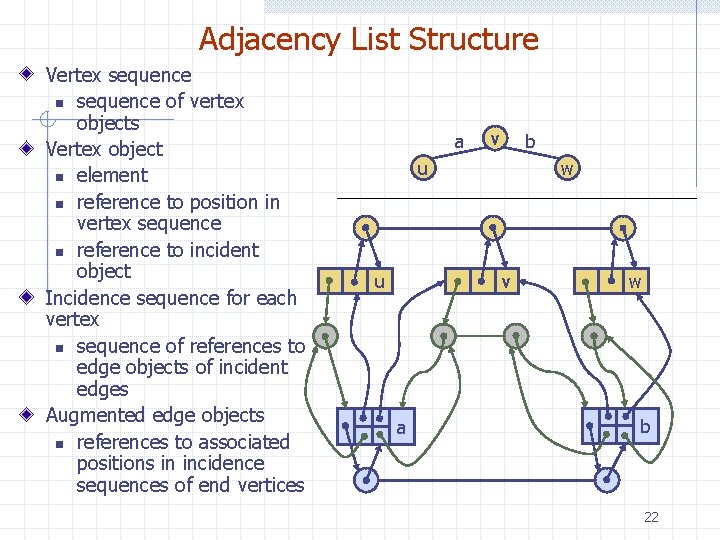
Adjacency List Structure Vertex sequence n sequence of vertex objects Vertex object n element n reference to position in vertex sequence n reference to incident object Incidence sequence for each vertex n sequence of references to edge objects of incident edges Augmented edge objects n references to associated positions in incidence sequences of end vertices a v b u u w v a w b 22

Adjacency List Structure - Notes Typically the incident sequence is implemented as a list, but could use a dictionary or a priority queue if their characteristics are useful. Structure provides direct access from both the edges to the vertices and from the vertices to their incident edges. Structure matches the performance of the edge list representation, but has improved running time when the above characteristic can be exploited - i. e. given a vertex, return an iterator of incident edges. 23

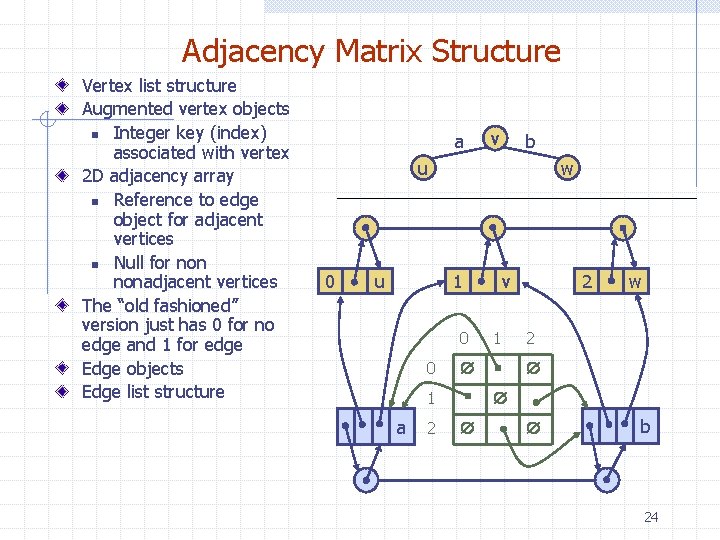
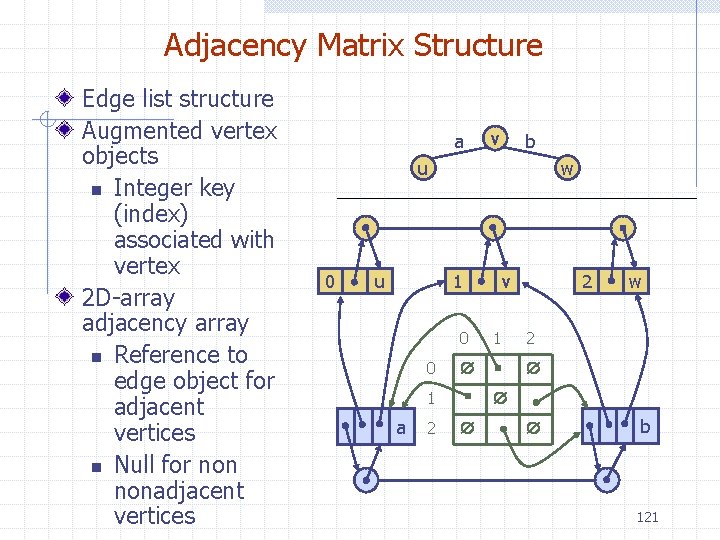
Adjacency Matrix Structure Vertex list structure Augmented vertex objects n Integer key (index) associated with vertex 2 D adjacency array n Reference to edge object for adjacent vertices n Null for nonadjacent vertices The “old fashioned” version just has 0 for no edge and 1 for edge Edge objects Edge list structure a v b u 0 u w 1 0 0 2 1 w 2 1 a 2 v b 24

Notes for Adjacency Matrix Historically, the adjacency matrix was the first represented as a Boolean matrix with A[i, j] = 1 if an edge existed between vertex i and j and 0 otherwise. The representation shown here updates this to a more object-oriented environment where you use an interface to access the structure. In all of these structures, additional data may be stored in vertex or edge objects. For example, if edges are being used in a problem about distances between to cities, those distances could be stored in the edge objects. 25

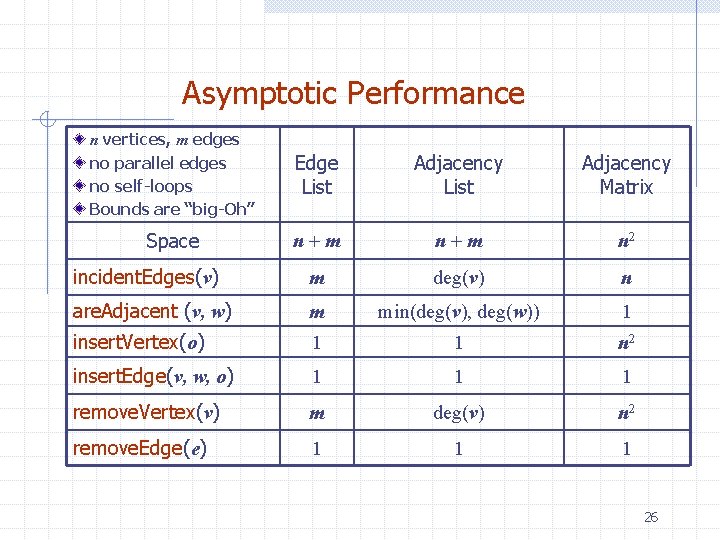
Asymptotic Performance n vertices, m edges no parallel edges no self-loops Bounds are “big-Oh” Edge List Adjacency Matrix Space n m n 2 incident. Edges(v) m deg(v) n are. Adjacent (v, w) m min(deg(v), deg(w)) 1 insert. Vertex(o) 1 1 n 2 insert. Edge(v, w, o) 1 1 1 remove. Vertex(v) m deg(v) n 2 remove. Edge(e) 1 1 1 26

Depth-First Search A B D C E

Outline and Reading Definitions (§ 6. 1) n Subgraph n Connectivity n Spanning trees and forests Depth-first search (§ 6. 3. 1) n Algorithm n Example n Properties n Analysis Applications of DFS (§ 6. 5) n Path finding n Cycle finding 28

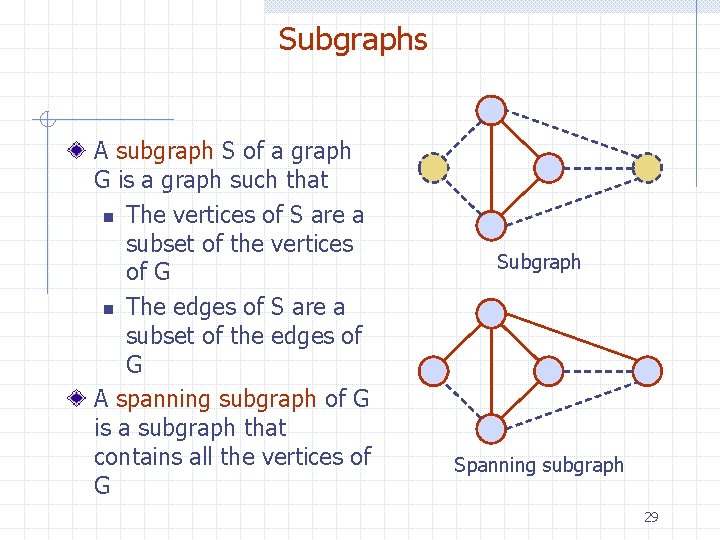
Subgraphs A subgraph S of a graph G is a graph such that n The vertices of S are a subset of the vertices of G n The edges of S are a subset of the edges of G A spanning subgraph of G is a subgraph that contains all the vertices of G Subgraph Spanning subgraph 29

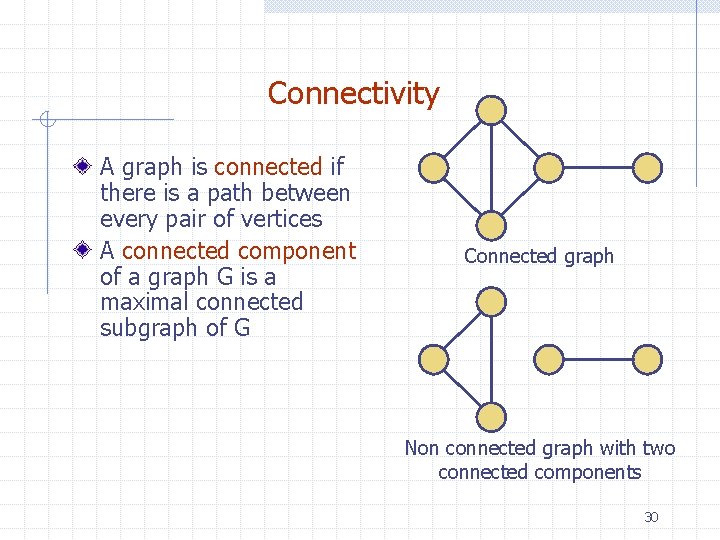
Connectivity A graph is connected if there is a path between every pair of vertices A connected component of a graph G is a maximal connected subgraph of G Connected graph Non connected graph with two connected components 30

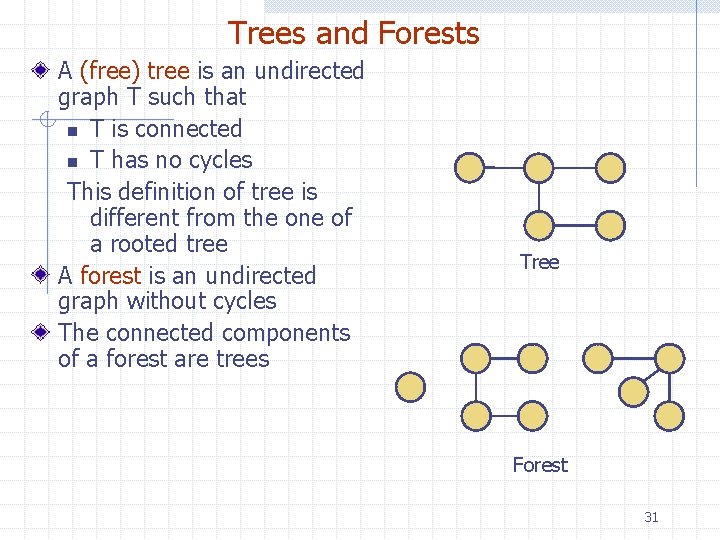
Trees and Forests A (free) tree is an undirected graph T such that n T is connected n T has no cycles This definition of tree is different from the one of a rooted tree A forest is an undirected graph without cycles The connected components of a forest are trees Tree Forest 31

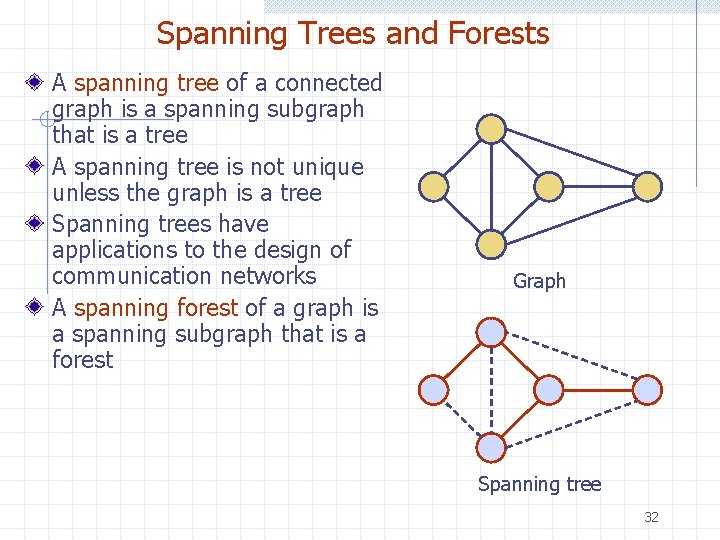
Spanning Trees and Forests A spanning tree of a connected graph is a spanning subgraph that is a tree A spanning tree is not unique unless the graph is a tree Spanning trees have applications to the design of communication networks A spanning forest of a graph is a spanning subgraph that is a forest Graph Spanning tree 32

Traversing a Graph A traversal of a graph is a systematic procedure for exploring a graph by examining all of its vertices and edges. Example: n Web spider or crawler is the data collecting part of a search engine that visits all the hypertext documents on the web. (The documents are vertices and the hyperlinks are the edges). 33

Depth-First Search Depth-first search (DFS) is a general technique for traversing a graph A DFS traversal of a graph G does the following: n Visits all the vertices and edges of G n Determines whether G is connected n Computes the connected components of G n Computes a spanning forest of G DFS on a graph with n vertices and m edges takes O(n m ) time DFS can be further extended to solve other graph problems n Find and report a path between two given vertices n Find a cycle in the graph n Depth-first search is to graphs what Euler tour is to binary trees 34

Depth-First Search DFS utilizes backtracking as you would if you were wandering through a maze. Start at a vertex in G with string; attached the string at the vertex; mark the vertex as "visited". Explore G by moving out along the incident edges according to some predetermined scheme for ordering and unroll the string. If you can move to a new vertex, mark it as "visited". If you hit a "visited" node, backtrack to the last vertex rolling up the string as you go and see if we can move out from there. The process terminates when the backtracking returns to the place where the string was attached - i. e. the start vertex. 35

Depth-First Search It's useful to distinguish edges by their use: Discovery (or tree) edges - those that are followed to discover new vertices. n Back edges - those that lead to already visited vertices. w For back edges, you need to backtrack to the last visited node and decide if you can move out from it without hitting a visited node. The discovery edges form a spanning tree of the connected components of the starting vertex - called a DFS tree. The back edges are also useful - assuming the DFS tree is rooted at the starting vertex, each back edge leads back from a vertex in the tree to one of its ancestors in 36 the tree. n

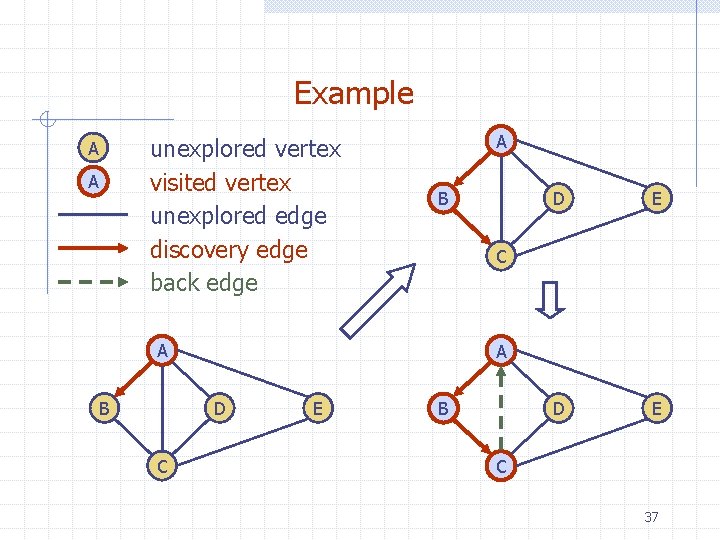
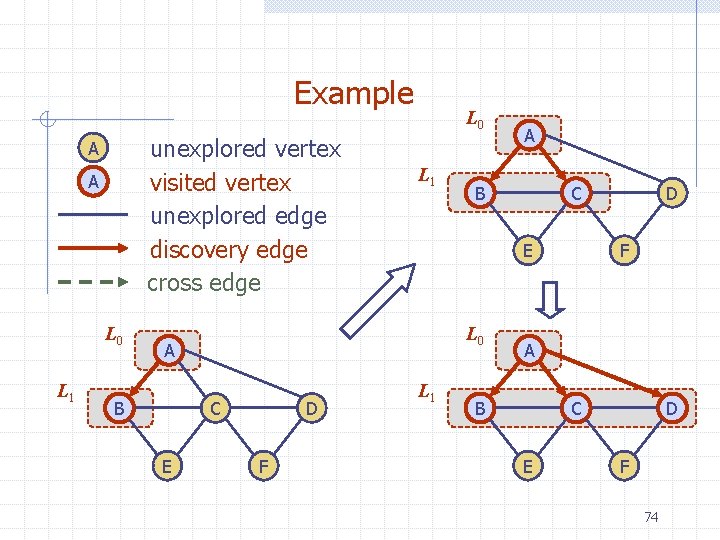
Example unexplored vertex visited vertex unexplored edge discovery edge back edge A A A B D E A D C E C A B D E B C 37

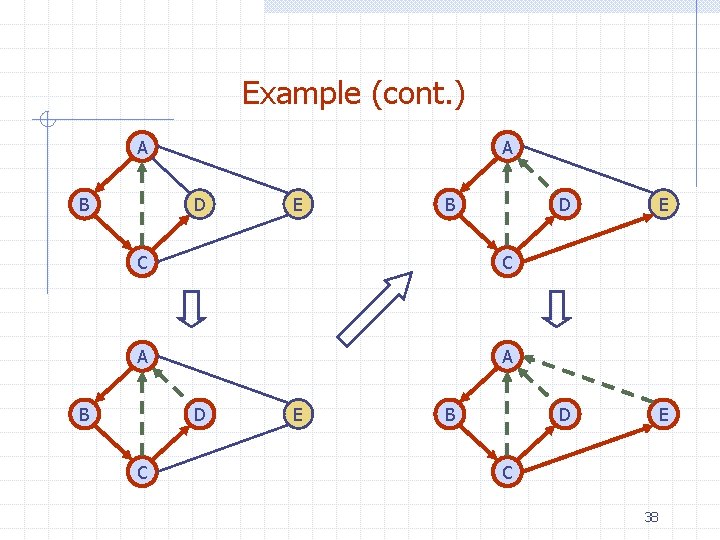
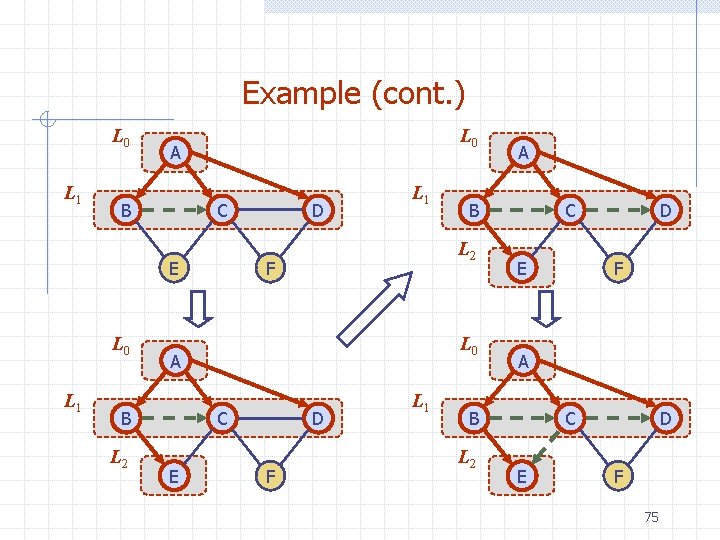
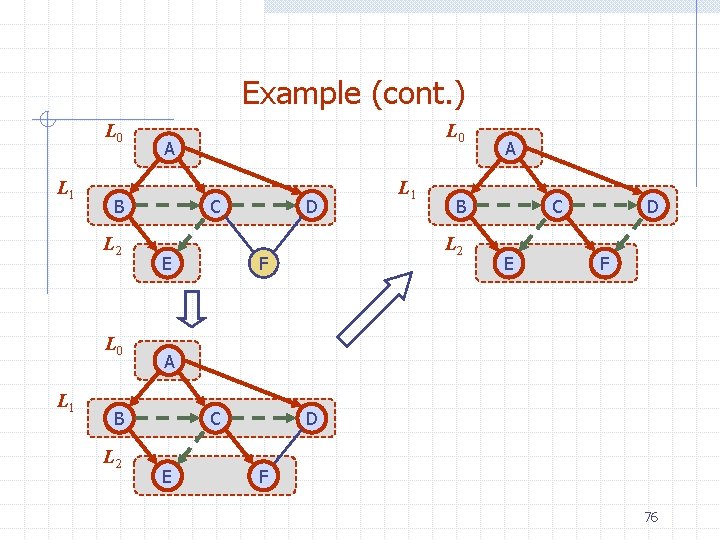
Example (cont. ) A B A D E B C C A A B D C E B D E C 38

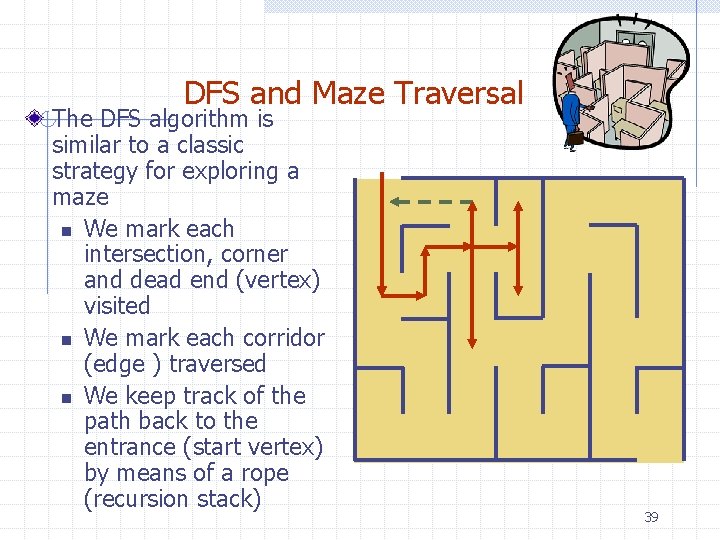
DFS and Maze Traversal The DFS algorithm is similar to a classic strategy for exploring a maze n We mark each intersection, corner and dead end (vertex) visited n We mark each corridor (edge ) traversed n We keep track of the path back to the entrance (start vertex) by means of a rope (recursion stack) 39

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 0 1 0 1 0 0 1 -1 1 0 0 0 0 1 1 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 40

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 0 1 0 1 0 0 1 -1 1 0 0 0 0 1 X 1 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 41

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 0 1 0 1 0 0 1 -1 1 0 0 0 0 1 X X 1 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 42

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 0 0 1 -1 1 1 0 0 X X X 1 0 0 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 43

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 0 0 0 X X X 0 1 X 1 0 0 0 1 -1 1 0 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 44

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 X 1 0 1 X X 0 0 0 X X 1 0 0 1 -1 1 0 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 45

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 1 0 1 X X 0 0 0 X X 1 0 0 1 -1 1 0 0 0 0 X 1 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 46

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 1 0 1 X X 0 0 0 X X 1 0 0 X X 0 0 1 -1 1 0 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 47

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 1 0 1 X X 0 0 0 X X 1 0 0 X X 0 1 -1 1 0 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 48

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 1 0 1 X X 0 0 0 X X 1 0 0 X X 0 1 -1 1 0 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S 49

Often Posed as Programming Contest Problem Given a maze represented as follows: 0 0 0 1 1 0 1 X X 0 0 0 X X 1 0 1 X 1 -1 X X 1 0 0 0 0 1=wall , -1=exit. Start at the bottom. To walk systematically, we'll try to go N, W, E, S The exact path taken depends on this ordering. 50

DFS Algorithm The algorithm uses a mechanism for setting and getting “labels” of vertices and edges Algorithm DFS(G) Input graph G Output labeling of the edges of G as discovery edges and back edges for all u G. vertices() set. Label(u, UNEXPLORED) for all e G. edges() set. Label(e, UNEXPLORED) for all v G. vertices() if get. Label(v) = UNEXPLORED DFS(G, v) Algorithm DFS(G, v) Input graph G and a start vertex v of G Output labeling of the edges of G in the connected component of v as discovery edges and back edges set. Label(v, VISITED) for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w G. opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) DFS(G, w) else set. Label(e, BACK) 51

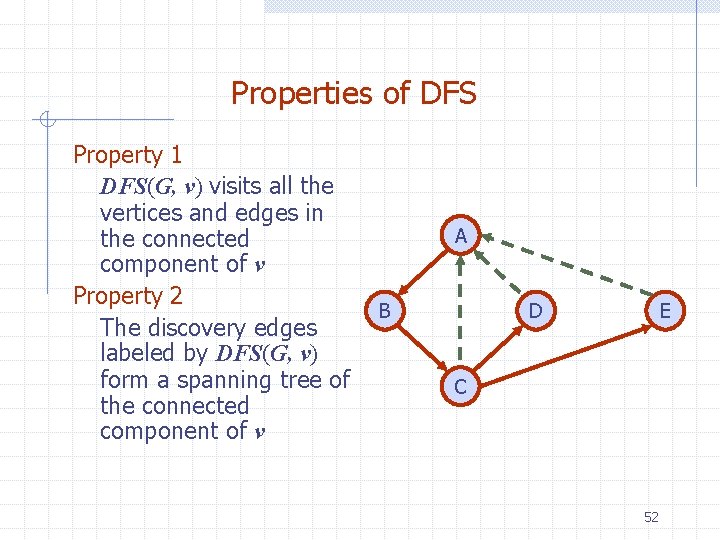
Properties of DFS Property 1 DFS(G, v) visits all the vertices and edges in the connected component of v Property 2 The discovery edges labeled by DFS(G, v) form a spanning tree of the connected component of v A B D E C 52

Analysis of DFS Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice n once as UNEXPLORED n once as VISITED Each edge is labeled twice n once as UNEXPLORED n once as DISCOVERY or BACK Method incident. Edges is called once for each vertex DFS runs in O(n m) time provided the graph is represented by the adjacency list structure n Recall that Sv deg(v) = 2 m 53

Path Finding We can specialize the DFS algorithm to find a path between two given vertices u and z We call DFS(G, u) with u as the start vertex We use a stack S to keep track of the path between the start vertex and the current vertex As soon as destination vertex z is encountered, we return the path as the contents of the stack Algorithm path. DFS(G, v, z) set. Label(v, VISITED) S. push(v) if v = z return S. elements() for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) S. push(e) path. DFS(G, w, z) S. pop() { e gets popped } else set. Label(e, BACK) S. pop() { v gets popped } 54

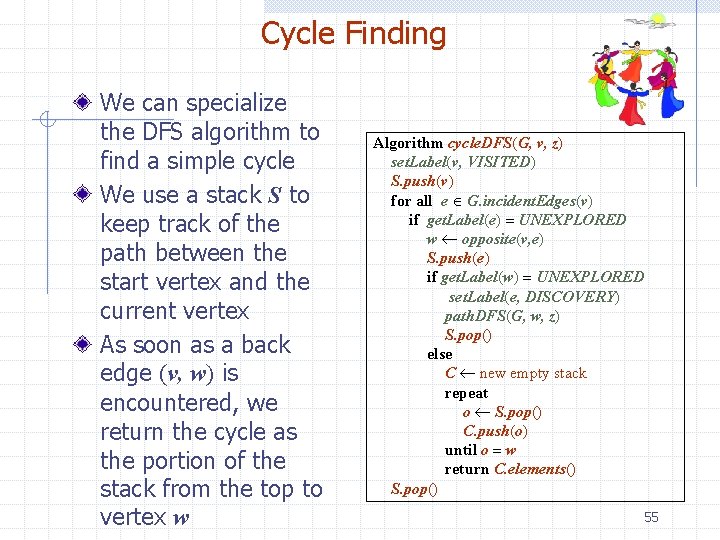
Cycle Finding We can specialize the DFS algorithm to find a simple cycle We use a stack S to keep track of the path between the start vertex and the current vertex As soon as a back edge (v, w) is encountered, we return the cycle as the portion of the stack from the top to vertex w Algorithm cycle. DFS(G, v, z) set. Label(v, VISITED) S. push(v) for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) S. push(e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) path. DFS(G, w, z) S. pop() else C new empty stack repeat o S. pop() C. push(o) until o = w return C. elements() S. pop() 55

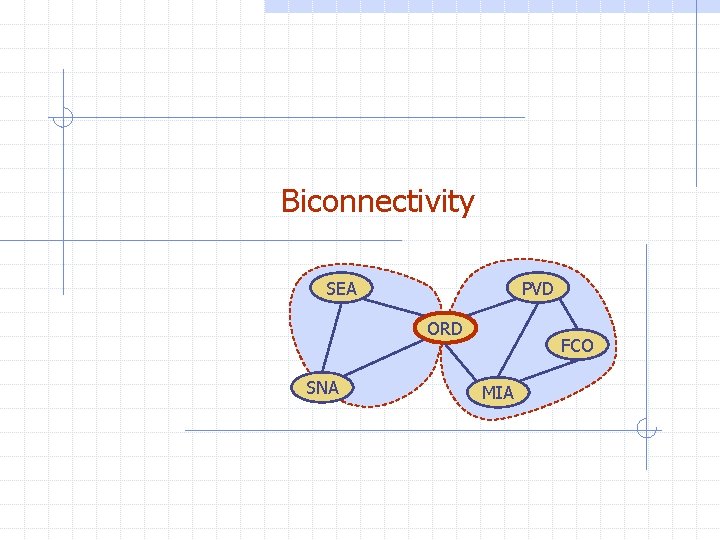
Biconnectivity SEA PVD ORD SNA FCO MIA

Outline and Reading Definitions (§ 6. 3. 2) n n n Separation vertices and edges Biconnected graph Biconnected components Equivalence classes Linked edges and link components Algorithms (§ 6. 3. 2) n n Auxiliary graph Proxy graph 57

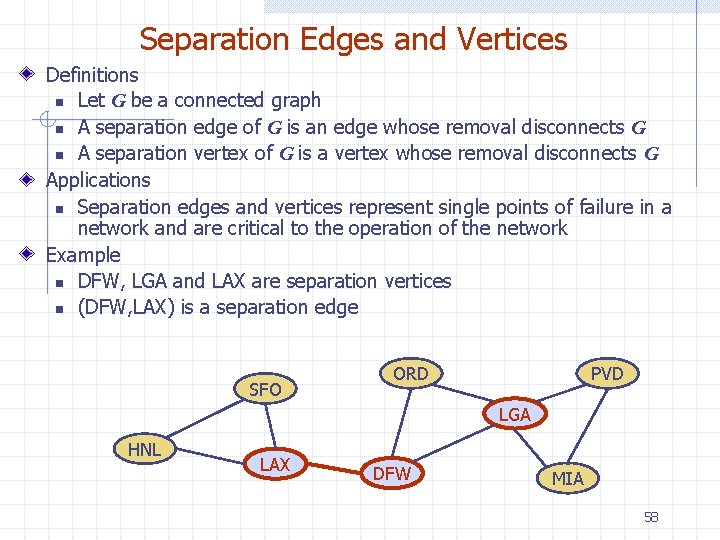
Separation Edges and Vertices Definitions n Let G be a connected graph n A separation edge of G is an edge whose removal disconnects G n A separation vertex of G is a vertex whose removal disconnects G Applications n Separation edges and vertices represent single points of failure in a network and are critical to the operation of the network Example n DFW, LGA and LAX are separation vertices n (DFW, LAX) is a separation edge SFO ORD PVD LGA HNL LAX DFW MIA 58

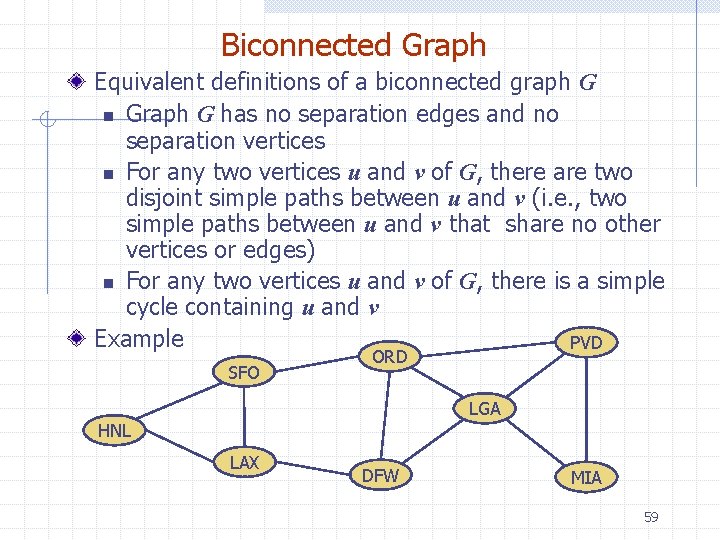
Biconnected Graph Equivalent definitions of a biconnected graph G n Graph G has no separation edges and no separation vertices n For any two vertices u and v of G, there are two disjoint simple paths between u and v (i. e. , two simple paths between u and v that share no other vertices or edges) n For any two vertices u and v of G, there is a simple cycle containing u and v Example PVD SFO ORD LGA HNL LAX DFW MIA 59

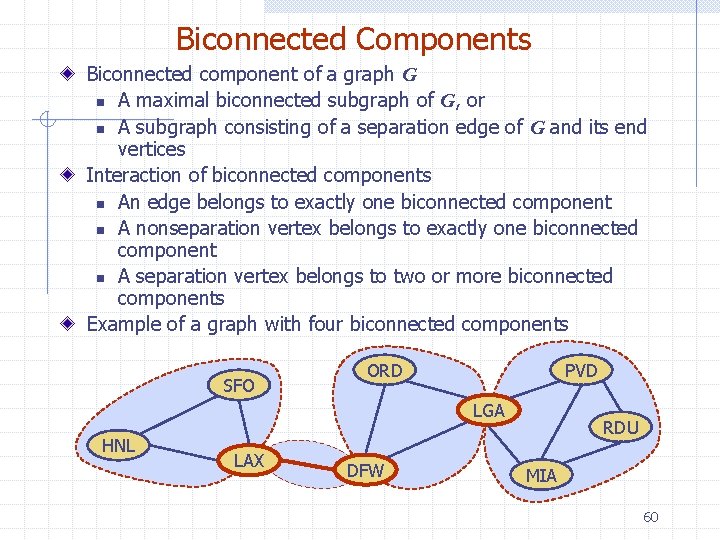
Biconnected Components Biconnected component of a graph G n A maximal biconnected subgraph of G, or n A subgraph consisting of a separation edge of G and its end vertices Interaction of biconnected components n An edge belongs to exactly one biconnected component n A nonseparation vertex belongs to exactly one biconnected component n A separation vertex belongs to two or more biconnected components Example of a graph with four biconnected components SFO ORD PVD LGA HNL LAX DFW RDU MIA 60

Equivalence Classes Given a set S, a relation R on S is a set of ordered pairs of elements of S, i. e. , R is a subset of S S An equivalence relation R on S satisfies the following properties Reflexive: (x, x) R Symmetric: (x, y) R (y, x) R Transitive: (x, y) R (y, z) R (x, z) R An equivalence relation R on S induces a partition of the elements of S into equivalence classes (i. e. the classes are pairwise disjoint and their union is S. Example (connectivity relation among the vertices of a graph): n Let V be the set of vertices of a graph G n Define the relation C = {(v, w) V V such that G has a path from v to w} n Relation C is an equivalence relation n The equivalence classes of relation C are the vertices in each connected component of graph G 61

Equivalence Relations These abstract the notion of equality for numbers. Obviously, equality for numbers is an equivalence relation. But, there are many such equivalence relations. Example: For positive integers a, b, c, d, define for fractions, a/b = c/d if and only if ad=bc. Proof: reflexive: a/b = a/b because ab=ba symmetric: a/b = c/d implies c/d = a/b because ad=bc implies cb=da. So, c/d=a/b transitive: a/b = c/d and c/d = e/f implies a/b = e/f (complete this proof) 62

Equivalence Relations What are the equivalence classes of the last equivalence relation? [1/2] = {x/y | 1/2= x/y} i. e. all the positive fractions we view as having 1/2 as its reduced form. i. e. [1/2] = {1/2, 2/4, 3/6, 4/8, . . . } Note: There is really nothing special about 1/2, [2/4], [3/6], [4/8]. . . are all [1/2]. 63

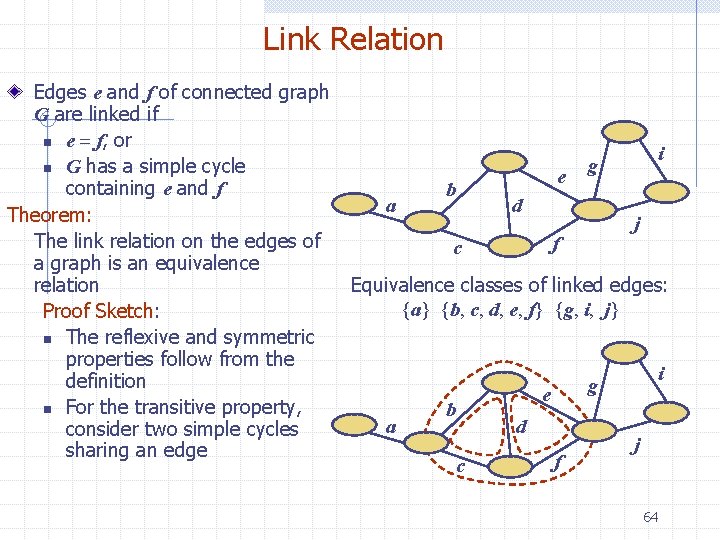
Link Relation Edges e and f of connected graph G are linked if n e = f, or n G has a simple cycle containing e and f Theorem: The link relation on the edges of a graph is an equivalence relation Proof Sketch: n The reflexive and symmetric properties follow from the definition n For the transitive property, consider two simple cycles sharing an edge a b e d j f c i g Equivalence classes of linked edges: {a} {b, c, d, e, f} {g, i, j} a b c i g e d f j 64

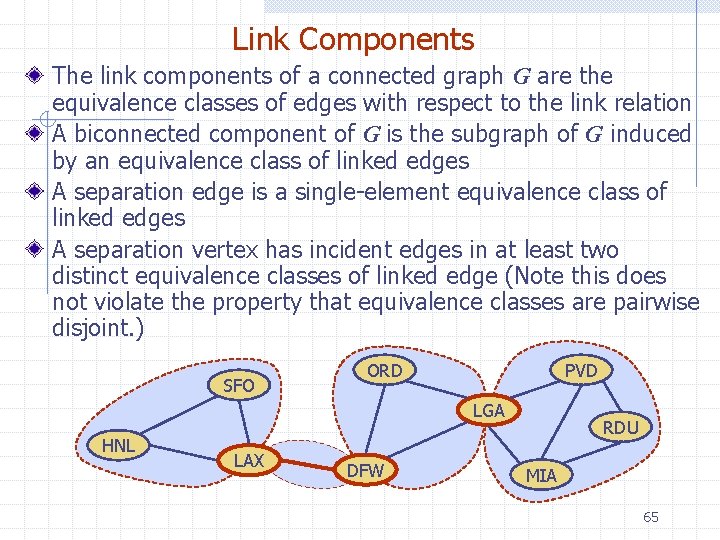
Link Components The link components of a connected graph G are the equivalence classes of edges with respect to the link relation A biconnected component of G is the subgraph of G induced by an equivalence class of linked edges A separation edge is a single-element equivalence class of linked edges A separation vertex has incident edges in at least two distinct equivalence classes of linked edge (Note this does not violate the property that equivalence classes are pairwise disjoint. ) SFO ORD PVD LGA HNL LAX DFW RDU MIA 65

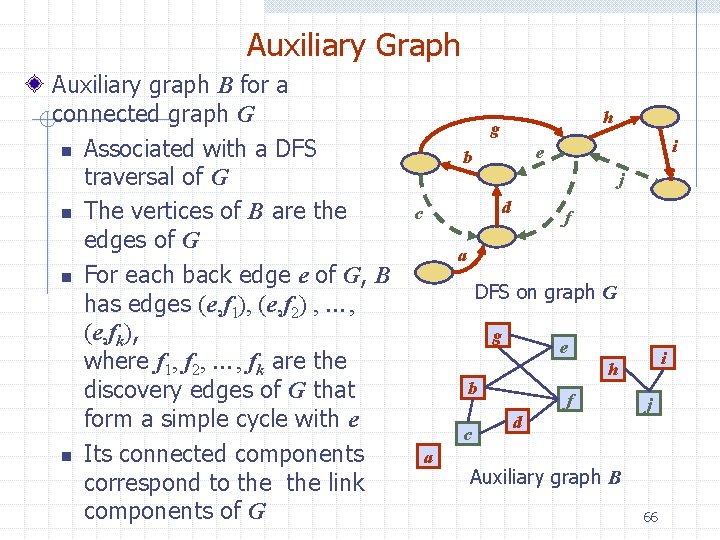
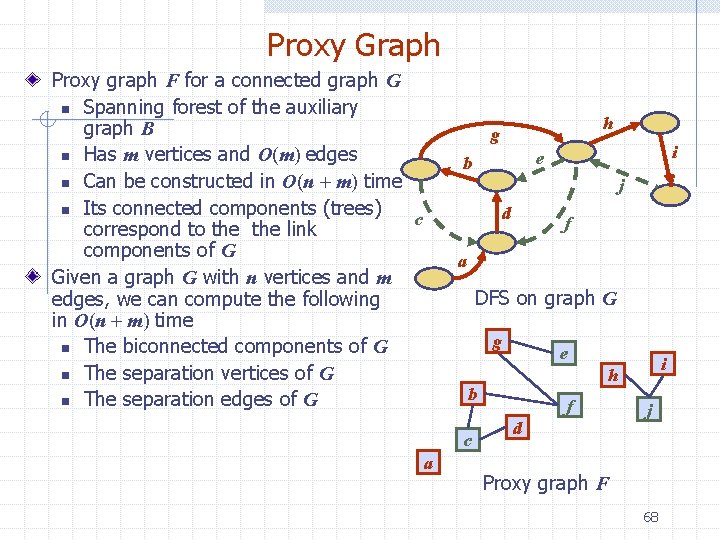
Auxiliary Graph Auxiliary graph B for a connected graph G n Associated with a DFS traversal of G n The vertices of B are the edges of G n For each back edge e of G, B has edges (e, f 1), (e, f 2) , …, (e, fk), where f 1, f 2, …, fk are the discovery edges of G that form a simple cycle with e n Its connected components correspond to the link components of G h g i e b i j d c f a DFS on graph G g e b c a i h f d j Auxiliary graph B 66

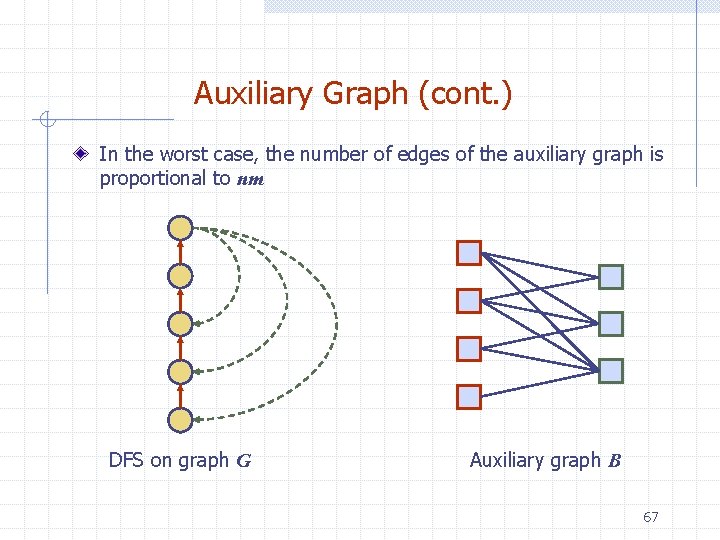
Auxiliary Graph (cont. ) In the worst case, the number of edges of the auxiliary graph is proportional to nm DFS on graph G Auxiliary graph B 67

Proxy Graph Proxy graph F for a connected graph G n Spanning forest of the auxiliary graph B n Has m vertices and O(m) edges n Can be constructed in O(n m) time n Its connected components (trees) c correspond to the link components of G Given a graph G with n vertices and m edges, we can compute the following in O(n m) time n The biconnected components of G n The separation vertices of G n The separation edges of G h g i e b i j d f a DFS on graph G g e b c a i h f d j Proxy graph F 68

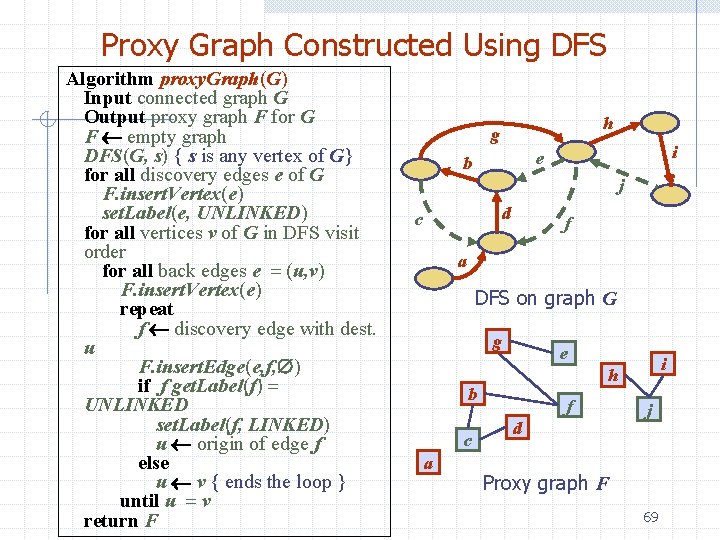
Proxy Graph Constructed Using DFS Algorithm proxy. Graph(G) Input connected graph G Output proxy graph F for G F empty graph DFS(G, s) { s is any vertex of G} for all discovery edges e of G F. insert. Vertex(e) set. Label(e, UNLINKED) for all vertices v of G in DFS visit order for all back edges e = (u, v) F. insert. Vertex(e) repeat f discovery edge with dest. u F. insert. Edge(e, f, ) if f get. Label(f) = UNLINKED set. Label(f, LINKED) u origin of edge f else u v { ends the loop } until u = v return F h g i e b i j d c f a DFS on graph G g e b c a i h f d j Proxy graph F 69

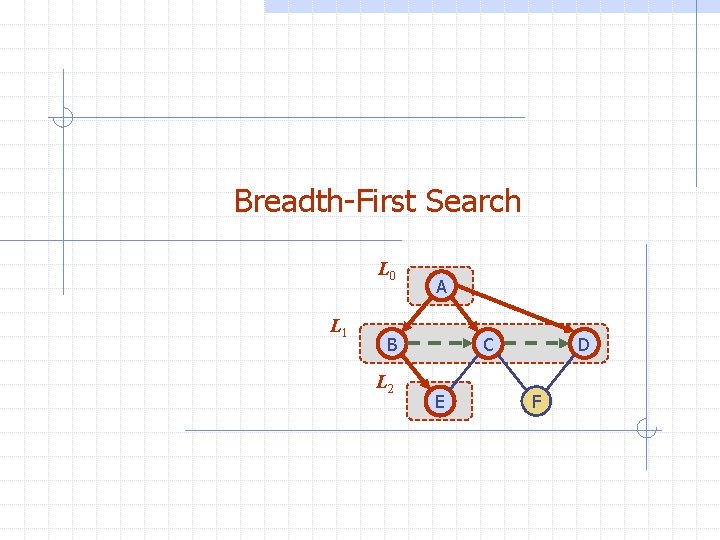
Breadth-First Search L 0 L 1 A B L 2 C E D F

Outline and Reading Breadth-first search (§ 6. 3. 3) n n n Algorithm Example Properties Analysis Applications DFS vs. BFS (§ 6. 3. 3) n n Comparison of applications Comparison of edge labels 71

Breadth-First Search Breadth-first search (BFS) is a general technique for traversing a graph A BFS traversal of a graph G n Visits all the vertices and edges of G n Determines whether G is connected n Computes the connected components of G n Computes a spanning forest of G BFS on a graph with n vertices and m edges takes O(n m ) time BFS can be further extended to solve other graph problems n Find and report a path with the minimum number of edges between two given vertices n Find a simple cycle, if there is one 72

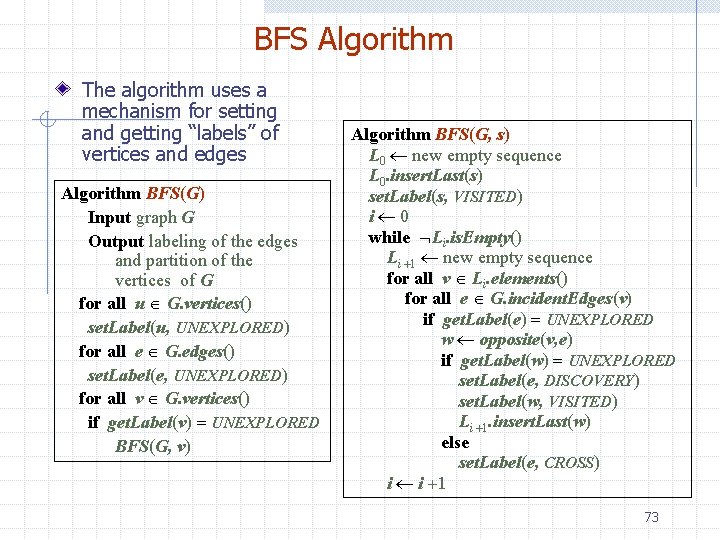
BFS Algorithm The algorithm uses a mechanism for setting and getting “labels” of vertices and edges Algorithm BFS(G) Input graph G Output labeling of the edges and partition of the vertices of G for all u G. vertices() set. Label(u, UNEXPLORED) for all e G. edges() set. Label(e, UNEXPLORED) for all v G. vertices() if get. Label(v) = UNEXPLORED BFS(G, v) Algorithm BFS(G, s) L 0 new empty sequence L 0. insert. Last(s) set. Label(s, VISITED) i 0 while Li. is. Empty() Li 1 new empty sequence for all v Li. elements() for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) set. Label(w, VISITED) Li 1. insert. Last(w) else set. Label(e, CROSS) i i 1 73

Example unexplored vertex visited vertex unexplored edge discovery edge cross edge A A L 0 L 1 L 0 C E B D F C E A B A L 1 D F A B C E D F 74

Example (cont. ) L 0 L 1 L 0 A B C E L 0 L 1 F L 0 C E B L 2 A B L 2 D L 1 D F L 1 A C E F A B L 2 D C E D F 75

Example (cont. ) L 0 L 1 A B L 2 C E D L 1 B L 2 F A C E D F A B L 2 L 0 C E D F 76

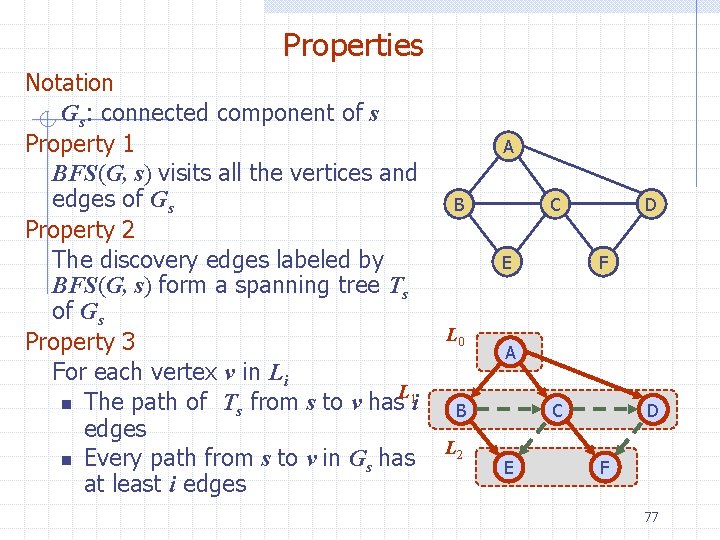
Properties Notation Gs: connected component of s Property 1 BFS(G, s) visits all the vertices and edges of Gs Property 2 The discovery edges labeled by BFS(G, s) form a spanning tree Ts of Gs Property 3 For each vertex v in Li L n The path of Ts from s to v has 1 i edges n Every path from s to v in Gs has at least i edges A B C E L 0 F A B L 2 D C E D F 77

Analysis Setting/getting a vertex/edge label takes O(1) time Each vertex is labeled twice n once as UNEXPLORED n once as VISITED Each edge is labeled twice n once as UNEXPLORED n once as DISCOVERY or CROSS Each vertex is inserted once into a sequence Li Method incident. Edges is called once for each vertex BFS runs in O(n m) time provided the graph is represented by the adjacency list structure n Recall that Sv deg(v) = 2 m 78

Applications We can specialize the BFS traversal of a graph G to solve the following problems in O(n m) time n Compute the connected components of G n Compute a spanning forest of G n Find a simple cycle in G, or report that G is a forest n Given two vertices of G, find a path in G between them with the minimum number of edges, or report that no such path exists 79

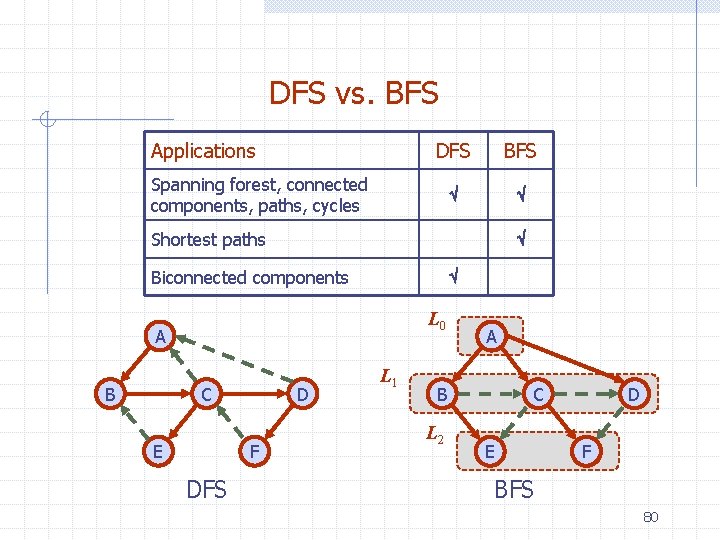
DFS vs. BFS Applications DFS BFS Spanning forest, connected components, paths, cycles Shortest paths Biconnected components L 0 A B C E D F DFS L 1 A B L 2 C E D F BFS 80

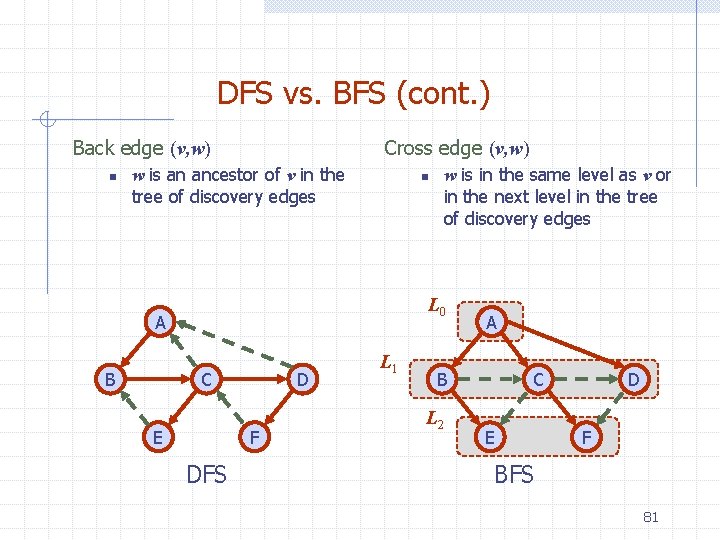
DFS vs. BFS (cont. ) Back edge (v, w) n Cross edge (v, w) w is an ancestor of v in the tree of discovery edges n L 0 A B w is in the same level as v or in the next level in the tree of discovery edges C E D F DFS L 1 A B L 2 C E D F BFS 81

Directed Graphs BOS ORD JFK SFO LAX DFW MIA

Outline and Reading (§ 6. 4) Reachability (§ 6. 4. 1) n Directed DFS n Strong connectivity Transitive closure (§ 6. 4. 2) n The Floyd-Warshall Algorithm Directed Acyclic Graphs (DAG’s) (§ 6. 4. 4) n Topological Sorting 83

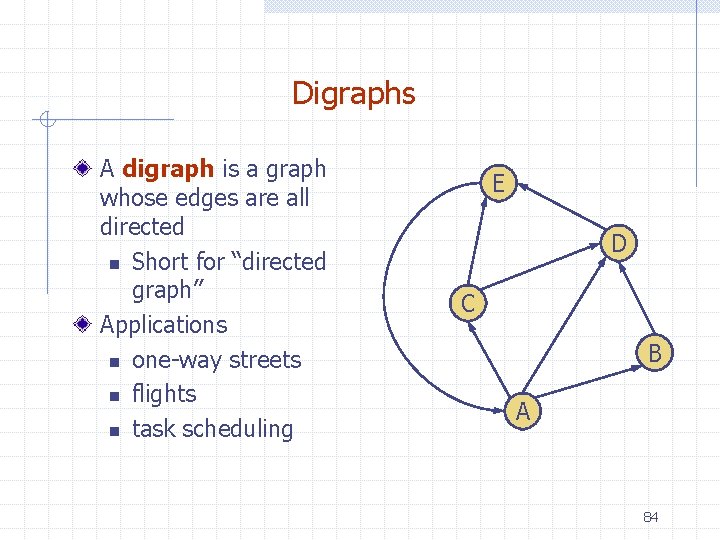
Digraphs A digraph is a graph whose edges are all directed n Short for “directed graph” Applications n one-way streets n flights n task scheduling E D C B A 84

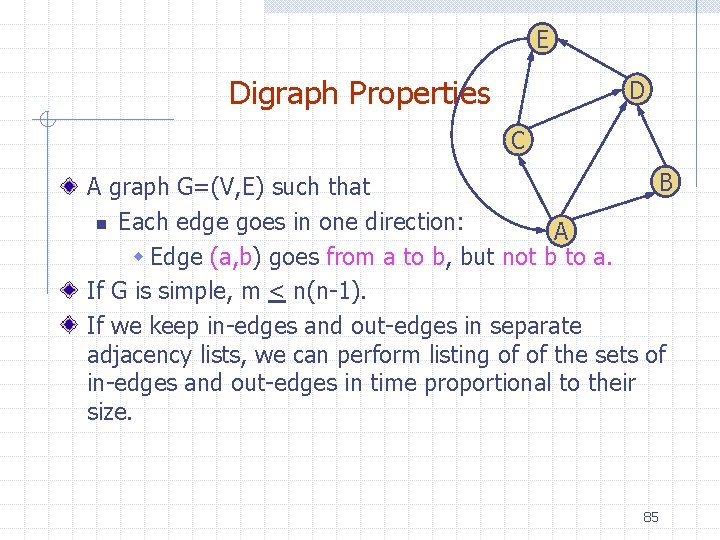
E Digraph Properties D C B A graph G=(V, E) such that n Each edge goes in one direction: A w Edge (a, b) goes from a to b, but not b to a. If G is simple, m < n(n-1). If we keep in-edges and out-edges in separate adjacency lists, we can perform listing of of the sets of in-edges and out-edges in time proportional to their size. 85

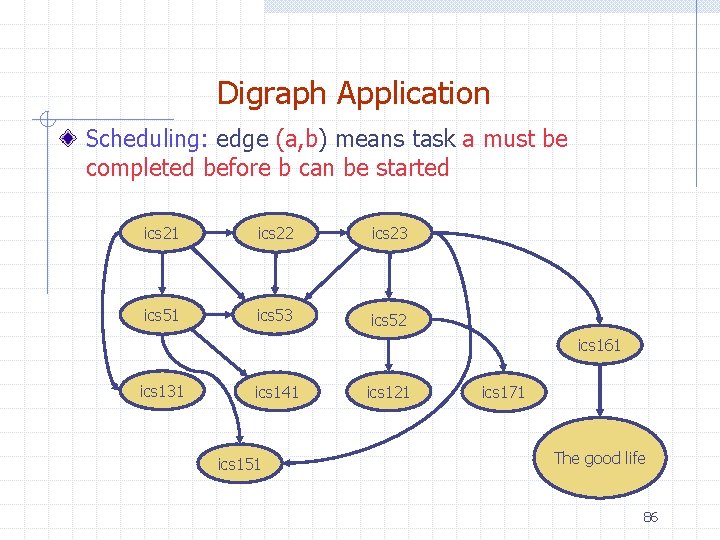
Digraph Application Scheduling: edge (a, b) means task a must be completed before b can be started ics 21 ics 22 ics 23 ics 51 ics 53 ics 52 ics 161 ics 131 ics 141 ics 151 ics 121 ics 171 The good life 86

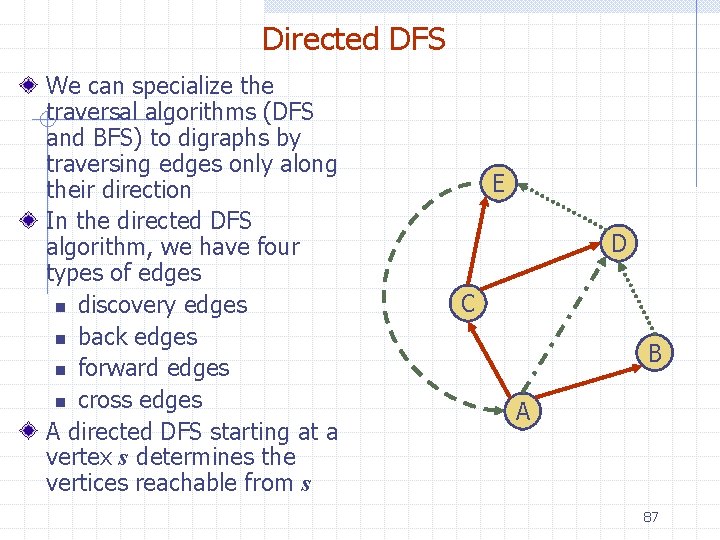
Directed DFS We can specialize the traversal algorithms (DFS and BFS) to digraphs by traversing edges only along their direction In the directed DFS algorithm, we have four types of edges n discovery edges n back edges n forward edges n cross edges A directed DFS starting at a vertex s determines the vertices reachable from s E D C B A 87

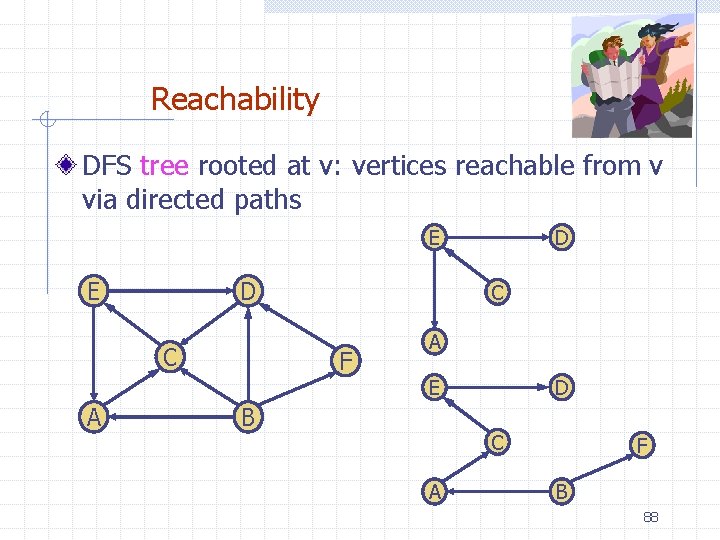
Reachability DFS tree rooted at v: vertices reachable from v via directed paths E E D C A D C F A E B D C A F B 88

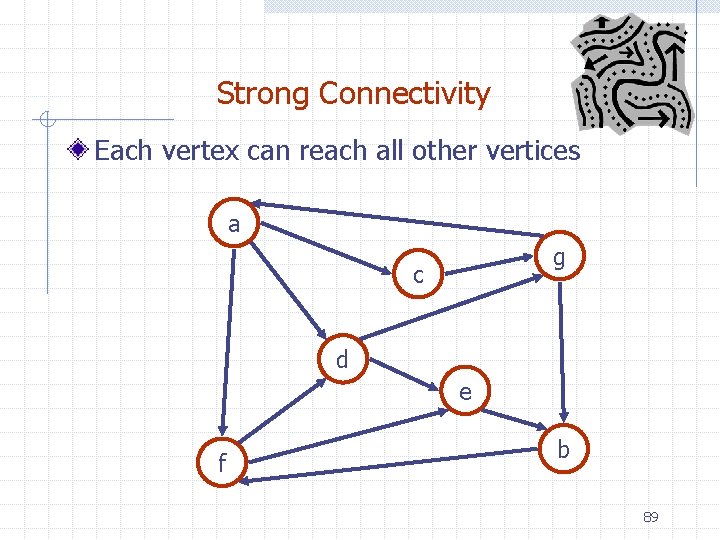
Strong Connectivity Each vertex can reach all other vertices a g c d e f b 89

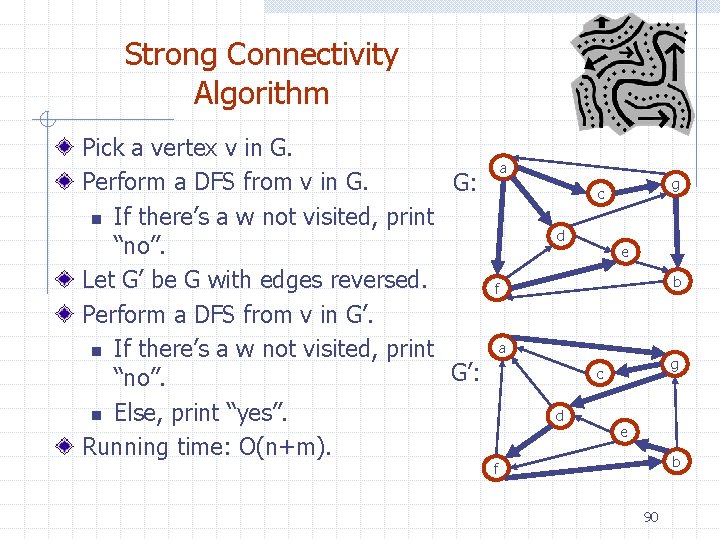
Strong Connectivity Algorithm Pick a vertex v in G. Perform a DFS from v in G. G: n If there’s a w not visited, print “no”. Let G’ be G with edges reversed. Perform a DFS from v in G’. n If there’s a w not visited, print G’: “no”. n Else, print “yes”. Running time: O(n+m). a g c d e b f 90

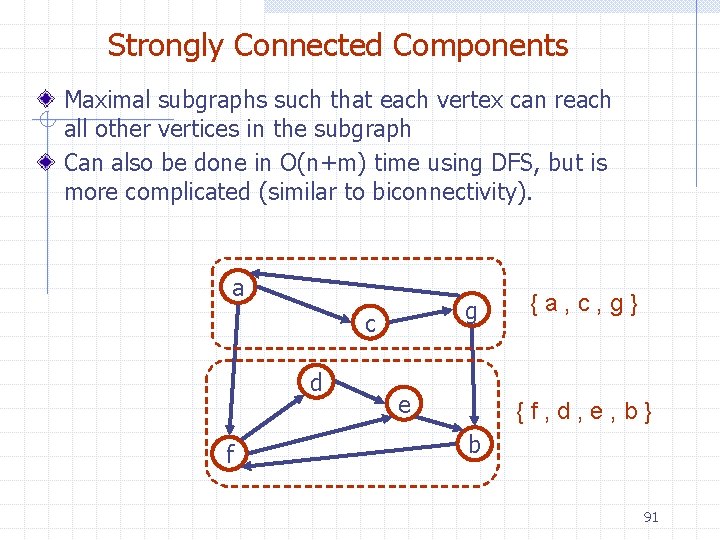
Strongly Connected Components Maximal subgraphs such that each vertex can reach all other vertices in the subgraph Can also be done in O(n+m) time using DFS, but is more complicated (similar to biconnectivity). a g c d f e {a, c, g} {f, d, e, b} b 91

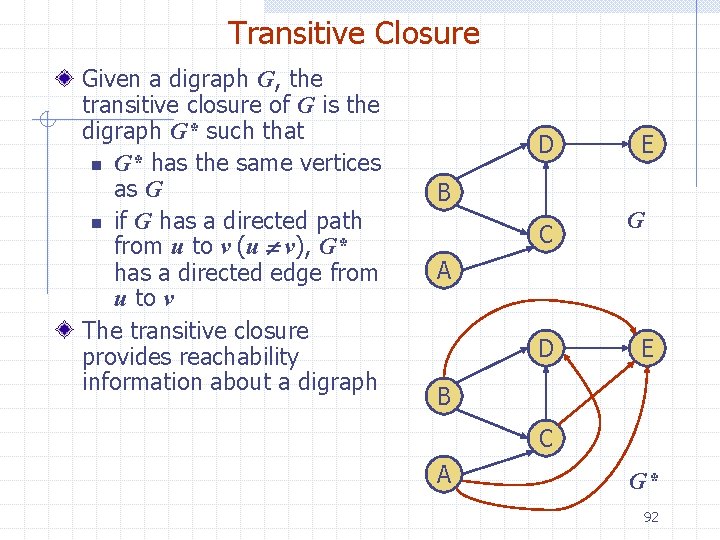
Transitive Closure Given a digraph G, the transitive closure of G is the digraph G* such that n G* has the same vertices as G n if G has a directed path from u to v (u v), G* has a directed edge from u to v The transitive closure provides reachability information about a digraph D E B C G A D E B C A G* 92

Computing the Transitive Closure We can perform DFS starting at each vertex n O(n(n+m)) If there's a way to get from A to B and from B to C, then there's a way to get from A to C. Alternatively. . . Use dynamic programming: the Floyd-Warshall Algorithm 93

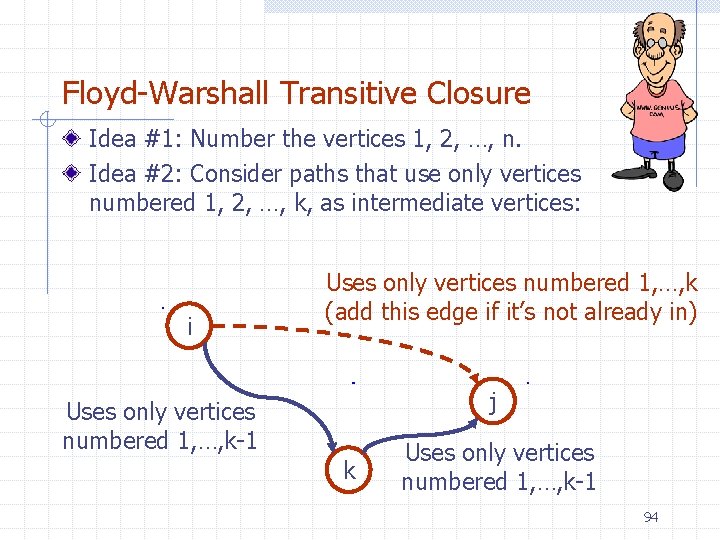
Floyd-Warshall Transitive Closure Idea #1: Number the vertices 1, 2, …, n. Idea #2: Consider paths that use only vertices numbered 1, 2, …, k, as intermediate vertices: i Uses only vertices numbered 1, …, k (add this edge if it’s not already in) j Uses only vertices numbered 1, …, k-1 k Uses only vertices numbered 1, …, k-1 94

Floyd-Warshall’s Algorithm Floyd. Warshall(G) Floyd-Warshall’s algorithm Input digraph G numbers the vertices of G as Output transitive closure G* of G v 1 , …, vn and computes a i 1 series of digraphs G 0, …, Gn for all v G. vertices() n G 0=G denote v as vi n Gk has a directed edge (vi, i i+1 vj) if G has a directed path G 0 G from vi to vj with for k 1 to n do intermediate vertices in Gk - 1 the set {v 1 , …, vk} for i 1 to n (i k) do We have that Gn = G* for j 1 to n (j i, k) do In phase k, digraph Gk is if Gk - 1. are. Adjacent(vi, vk) computed from Gk - 1. are. Adjacent(vk, vj) Running time: O(n 3), if Gk. are. Adjacent(vi, vj) assuming are. Adjacent is O(1) Gk. insert. Directed. Edge(vi, vj , k) (e. g. , adjacency matrix) return Gn 95

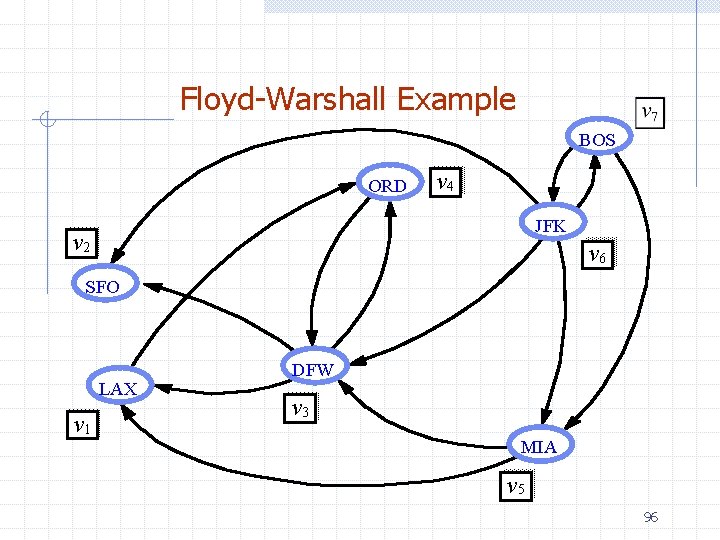
Floyd-Warshall Example BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 96

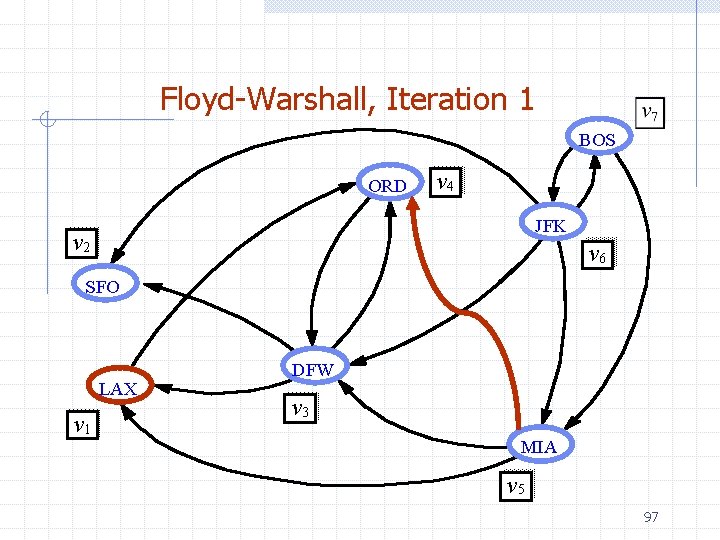
Floyd-Warshall, Iteration 1 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 97

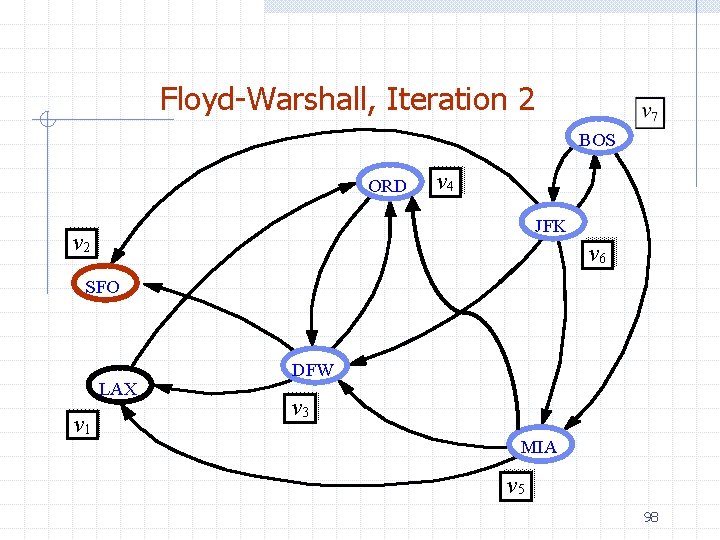
Floyd-Warshall, Iteration 2 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 98

Floyd-Warshall, Iteration 3 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 99

Floyd-Warshall, Iteration 4 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 100

Floyd-Warshall, Iteration 5 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 101

Floyd-Warshall, Iteration 6 BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 102

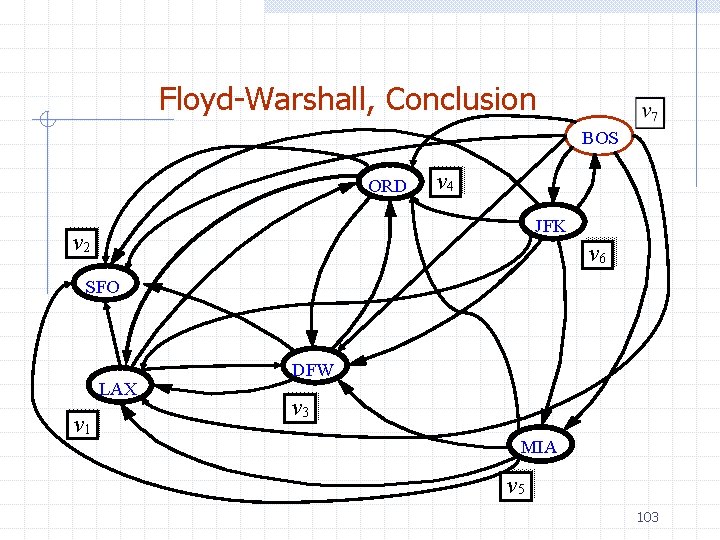
Floyd-Warshall, Conclusion BOS ORD v 4 JFK v 2 v 6 SFO LAX v 1 DFW v 3 MIA v 5 103

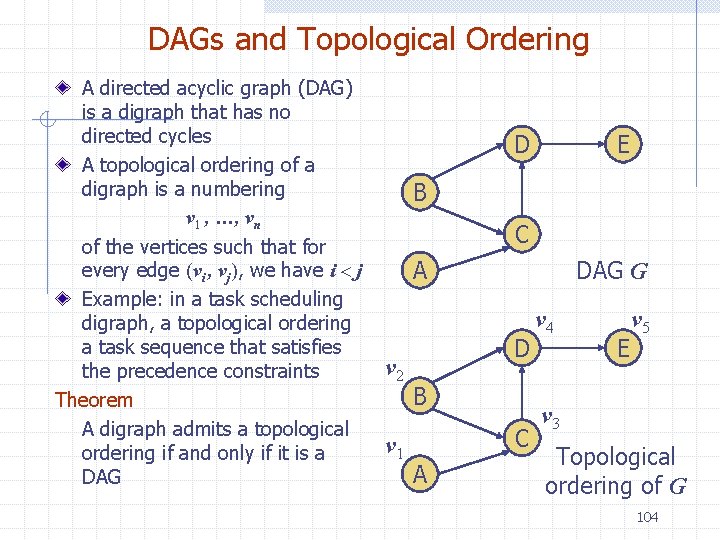
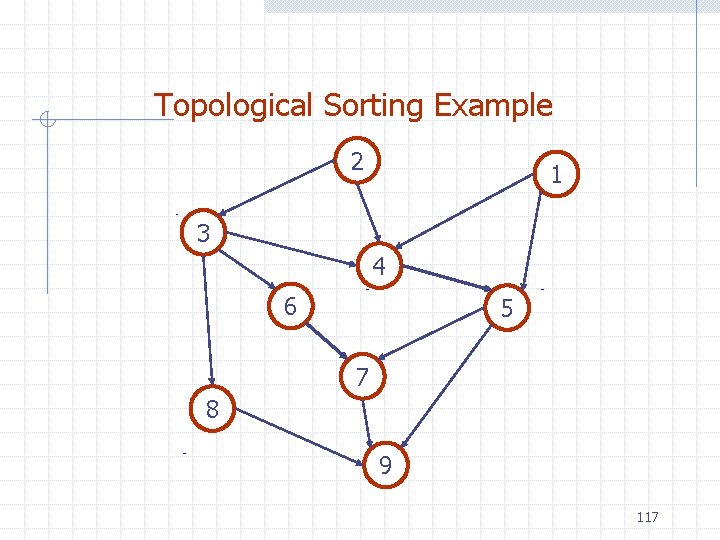
DAGs and Topological Ordering A directed acyclic graph (DAG) is a digraph that has no directed cycles A topological ordering of a digraph is a numbering v 1 , …, vn of the vertices such that for every edge (vi , vj), we have i < j Example: in a task scheduling digraph, a topological ordering a task sequence that satisfies the precedence constraints Theorem A digraph admits a topological ordering if and only if it is a DAG D E B C DAG G A v 2 v 1 D B C A v 4 E v 5 v 3 Topological ordering of G 104

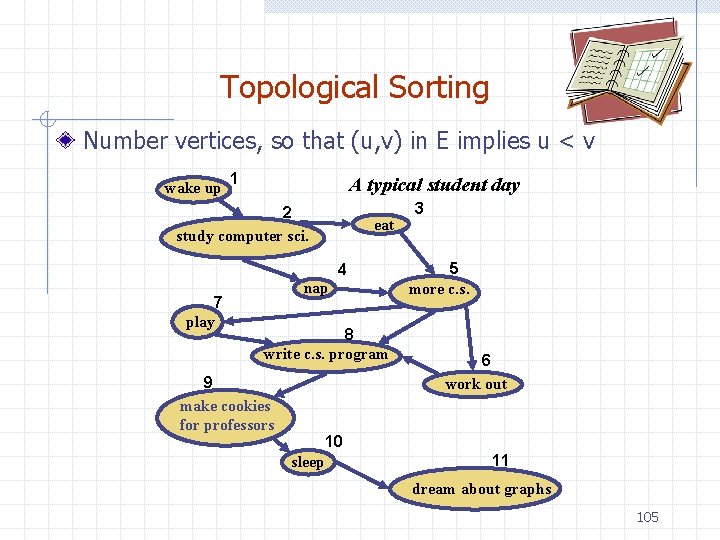
Topological Sorting Number vertices, so that (u, v) in E implies u < v wake up 1 A typical student day 2 study computer sci. eat 4 7 play nap 8 write c. s. program 9 make cookies for professors 3 5 more c. s. 6 work out 10 sleep 11 dream about graphs 105

Algorithm for Topological Sorting Note: This algorithm is different than the one in Goodrich-Tamassia Method Topological. Sort(G) H G // Temporary copy of G n G. num. Vertices() while H is not empty do Let v be a vertex with no outgoing edges Label v n n n-1 Remove v from H Running time: O(n + m). How…? 106

Topological Sorting Algorithm using DFS Simulate the algorithm by using depth-first search Algorithm topological. DFS(G) Input dag G Output topological ordering of G n G. num. Vertices() for all u G. vertices() set. Label(u, UNEXPLORED) for all e G. edges() set. Label(e, UNEXPLORED) for all v G. vertices() if get. Label(v) = UNEXPLORED topological. DFS(G, v) O(n+m) time. Algorithm topological. DFS(G, v) Input graph G and a start vertex v of G Output labeling of the vertices of G in the connected component of v set. Label(v, VISITED) for all e G. incident. Edges(v) if get. Label(e) = UNEXPLORED w opposite(v, e) if get. Label(w) = UNEXPLORED set. Label(e, DISCOVERY) topological. DFS(G, w) else {e is a forward or cross edge} Label v with topological number n n n-1 107

Topological Sorting Example 108

Topological Sorting Example 9 109

Topological Sorting Example 8 9 110

Topological Sorting Example 7 8 9 111

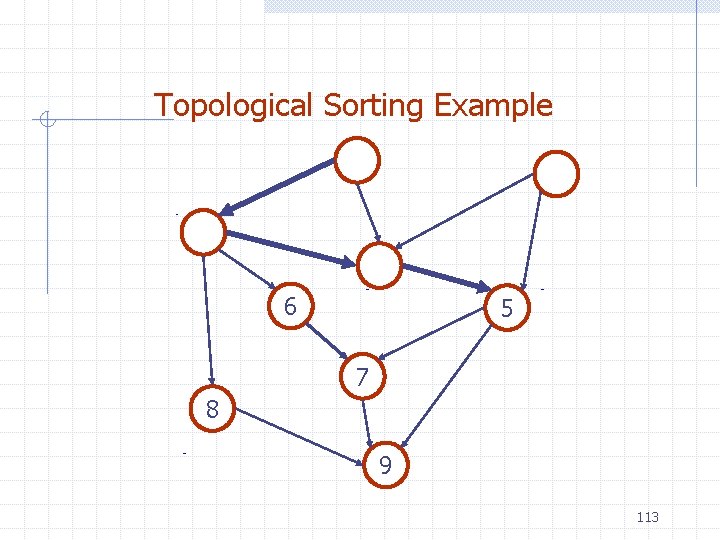
Topological Sorting Example 6 7 8 9 112

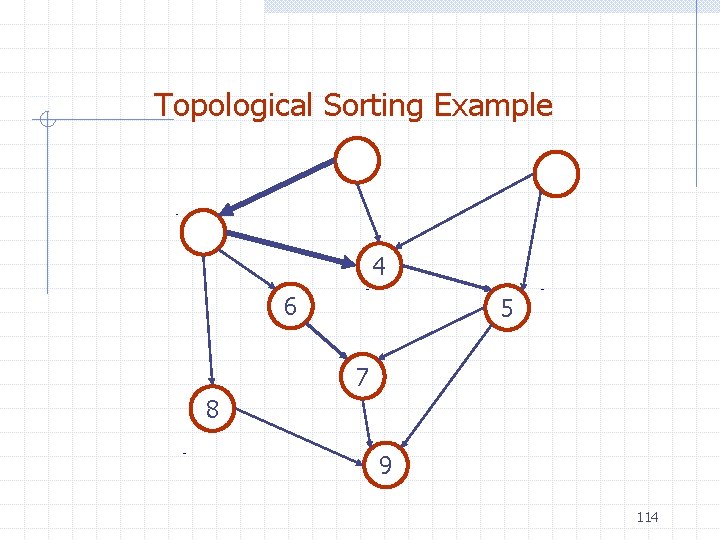
Topological Sorting Example 6 5 7 8 9 113

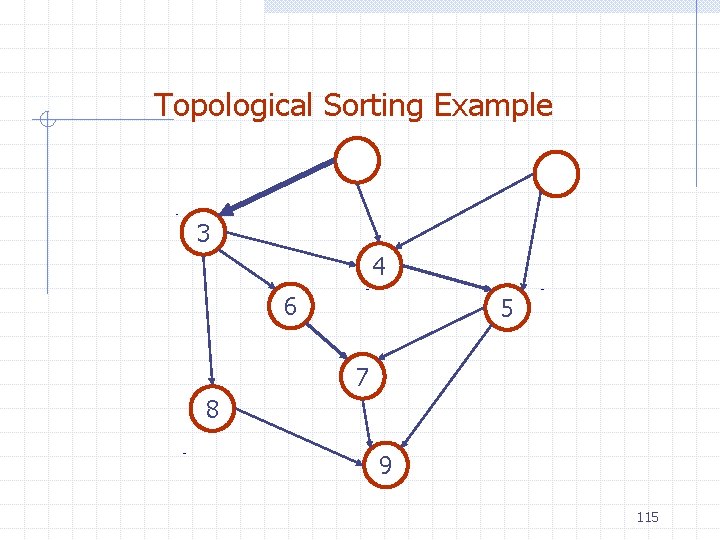
Topological Sorting Example 4 6 5 7 8 9 114

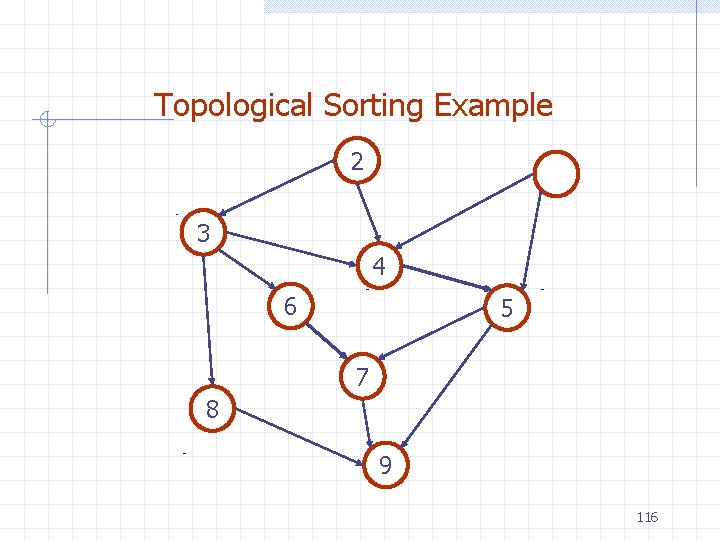
Topological Sorting Example 3 4 6 5 7 8 9 115

Topological Sorting Example 2 3 4 6 5 7 8 9 116

Topological Sorting Example 2 1 3 4 6 5 7 8 9 117

Campus Tour

Outline and Reading Review n Adjacency matrix structure (§ 6. 2. 3) n Kruskal’s MST algorithm (§ 7. 3. 1) Partition ADT and implementation (§ 4. 2. 2) The decorator pattern (§ 6. 5. 1) The traveling salesperson problem n Definition n Approximation algorithm (§ 13. 4. 3) 119

Graph Assignment Goals n Learn and implement the adjacency matrix structure an Kruskal’s minimum spanning tree algorithm n Understand use the decorator pattern and various JDSL classes and interfaces Our task n Implement the adjacency matrix structure for representing a graph n Implement Kruskal’s MST algorithm Frontend n Computation and visualization of an approximate traveling salesperson tour 120

Adjacency Matrix Structure Edge list structure Augmented vertex objects n Integer key (index) associated with vertex 2 D-array adjacency array n Reference to edge object for adjacent vertices n Null for nonadjacent vertices a v b u 0 u w 1 0 0 2 1 w 2 1 a 2 v b 121

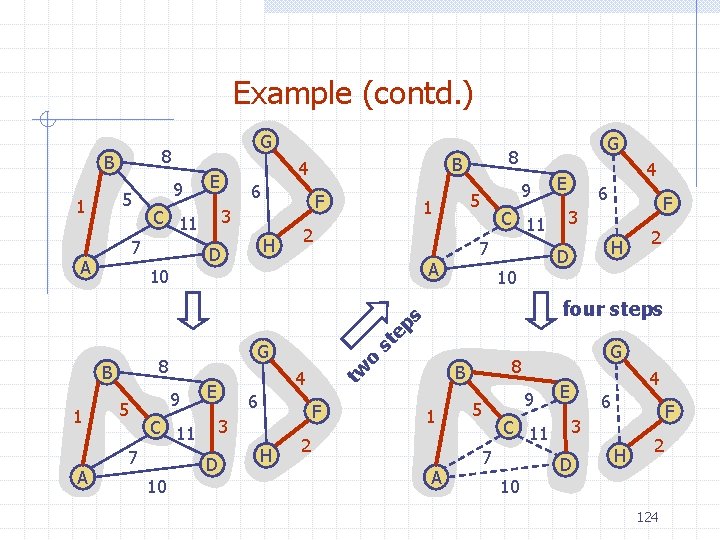
Kruskal’s Algorithm The vertices are partitioned into clouds n We start with one cloud per vertex n Clouds are merged during the execution of the algorithm Partition ADT: n make. Set(o): create set {o} and return a locator for object o n find(l): return the set of the object with locator l n union(A, B): merge sets A and B Algorithm Kruskal. MSF(G) Input weighted graph G Output labeling of the edges of a minimum spanning forest of G Q new heap-based priority queue for all v G. vertices() do l make. Set(v) { elementary cloud } set. Locator(v, l) for all e G. edges() do Q. insert(weight(e), e) while Q. is. Empty() e Q. remove. Min() [u, v] G. end. Vertices(e) A find(get. Locator(u)) B find(get. Locator(v)) if A B set. MSFedge(e) { merge clouds } union(A, B) 122

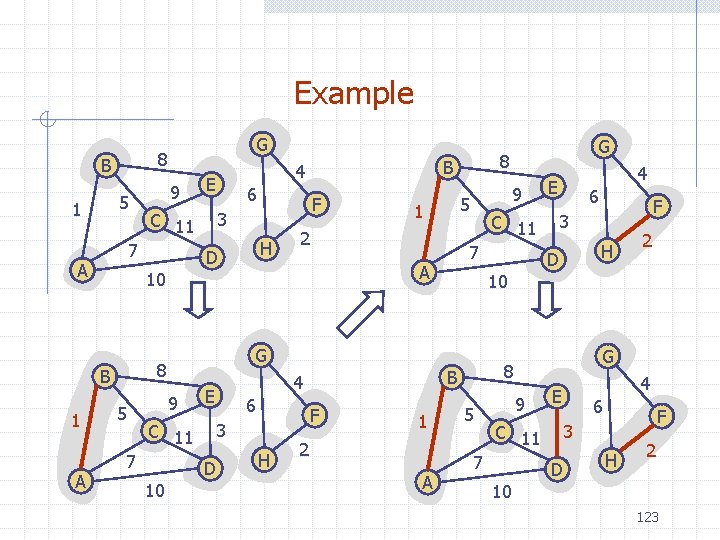
Example 8 B 5 1 6 3 C 11 10 9 5 1 2 C 11 7 A E 6 F 3 D H 1 2 A E 6 5 H C 11 10 2 G 9 7 F 3 8 B 4 4 D 10 G 9 7 H D 8 5 F G 8 B 4 E C 11 10 B A 9 7 A 1 G 4 E 6 F 3 D H 2 123

Example (contd. ) B 5 1 G 8 9 6 H D 9 5 1 2 C 11 7 A 1 A 5 9 C 11 7 10 F 3 D H 3 H 10 ep o 6 F 2 four steps G 8 B tw 4 E 6 st G 8 B 4 E D s 10 F 3 C 11 7 A E 8 B 4 G 1 2 A 5 9 C 11 7 10 4 E 6 F 3 D H 2 124

Partition Implementation Partition implementation A set is represented the sequence of its elements n A position stores a reference back to the sequence itself (for operation find) n The position of an element in the sequence serves as locator for the element in the set n In operation union, we move the elements of the smaller sequence into to the larger sequence Worst-case running times n make. Set, find: O(1) n union: O(min(n. A, n. B)) n Amortized analysis n n n Consider a series of k Partiton ADT operations that includes n make. Set operations Each time we move an element into a new sequence, the size of its set at least doubles An element is moved at most log 2 n times Moving an element takes O(1) time The total time for the series of operations is O(k n log n) 125

Analysis of Kruskal’s Algorithm Graph operations n Methods vertices and edges are called once n Method end. Vertices is called m times Priority queue operations n We perform m insert operations and m remove. Min operations Partition operations n We perform n make. Set operations, 2 m find operations and no more than n - 1 union operations Label operations n We set vertex labels n times and get them 2 m times Kruskal’s algorithm runs in time O((n m) log n) time provided the graph has no parallel edges and is represented by the adjacency list structure 126

Decorator Pattern Labels are commonly used in graph algorithms n Auxiliary data n Output Examples n DFS: unexplored/visited label for vertices and unexplored/ forward/back labels for edges n Dijkstra and Prim-Jarnik: distance, locator, and parent labels for vertices n Kruskal: locator label for vertices and MSF label for edges The decorator pattern extends the methods of the Position ADT to support the handling of attributes (labels) n has(a): tests whether the position has attribute a n get(a): returns the value of attribute a n set(a, x): sets to x the value of attribute a n destroy(a): removes attribute a and its associated value (for cleanup purposes) The decorator pattern can be implemented by storing a dictionary of (attribute, value) items at each position 127

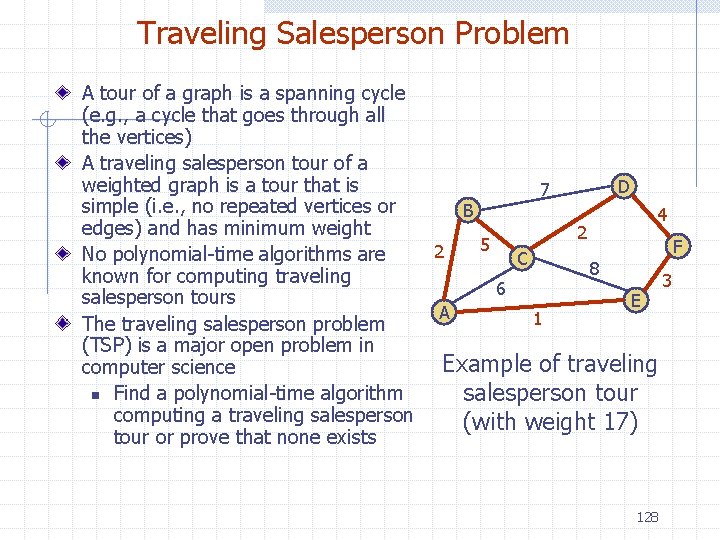
Traveling Salesperson Problem A tour of a graph is a spanning cycle (e. g. , a cycle that goes through all the vertices) A traveling salesperson tour of a weighted graph is a tour that is D 7 simple (i. e. , no repeated vertices or B 4 edges) and has minimum weight 2 5 F 2 No polynomial-time algorithms are C 8 known for computing traveling 3 6 salesperson tours E A 1 The traveling salesperson problem (TSP) is a major open problem in Example of traveling computer science n Find a polynomial-time algorithm salesperson tour computing a traveling salesperson (with weight 17) tour or prove that none exists 128

TSP Approximation We can approximate a TSP tour with a tour of at most twice the weight for the case of Euclidean graphs n Vertices are points in the plane n Every pair of vertices is connected by an edge n The weight of an edge is the length of the segment joining the points Approximation algorithm n Compute a minimum spanning tree n Form an Eulerian circuit around the MST n Transform the circuit into a tour 129