Python Stacks and Queues as an Array Damian

Python: Stacks and Queues (as an Array) Damian Gordon

Stacks

Stacks • A Stack is a pile of stuff: • It’s a structure that conforms to the principle of Last In, First Out (LIFO). • The last item to join the stack is the first item to be served.

Stacks • Values are added to the top: 67 59 53 26 59 41 31

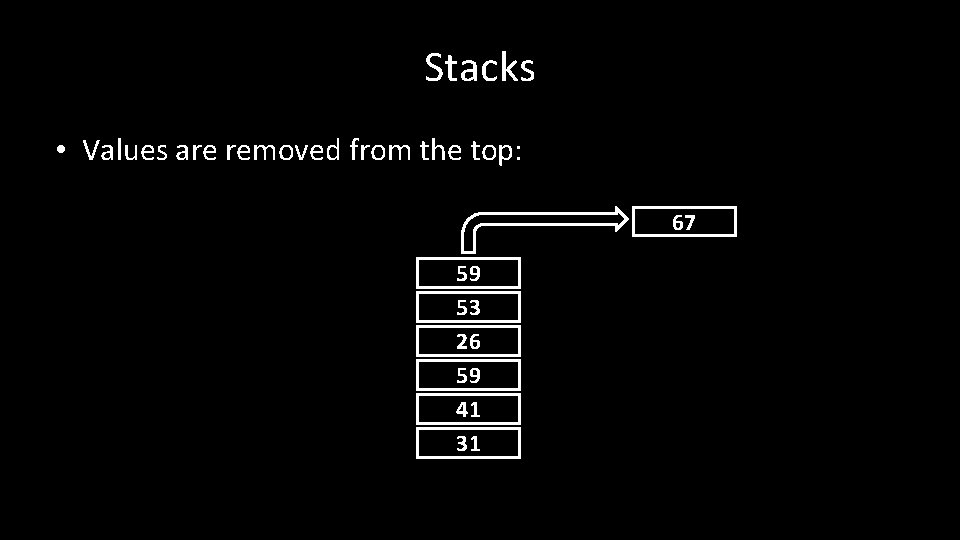
Stacks • Values are removed from the top: 67 59 53 26 59 41 31

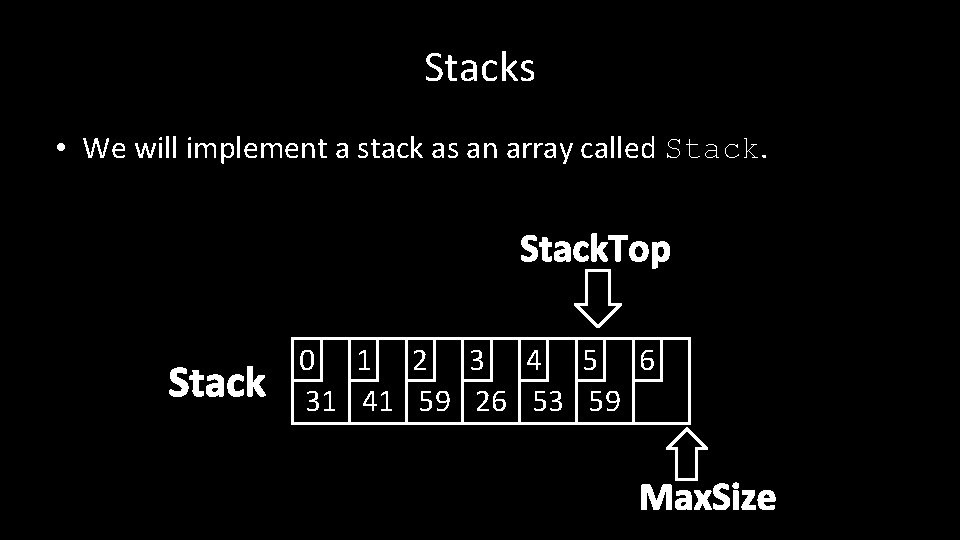
Stacks • We will implement a stack as an array called Stack. • The maximum length of the stack is called Max. Size. • The current top of the stack is called Stack. Top.

Stacks • We will implement a stack as an array called Stack. Top Stack 0 1 2 3 4 5 6 31 41 59 26 53 59 Max. Size

Stacks (Declaring) # PROGRAM Stack. As. Array: Stack = [31, 41, 59, 26, 0, 0, 0] Max. Size = 7 Stack. Top = 3 #END Stack. As. Array.

Stacks • We will look at implementing the following modules: • Is. Full() – Check if the stack is full • Is. Empty() – Check if the stack is full • Push(N) – Add a new item (N) to the top of the stack • Pop() – Remove the top value from the stack • Top() – Tell us what the top value of the stack is (without removing it).

Stacks (Is. Full) def Is. Full(): global Stack. Top if (Stack. Top + 1 == Max. Size): # THEN Stack. Full = True else: Stack. Full = False # ENDIF return Stack. Full #END Is. Full. Stack. Top Max. Size

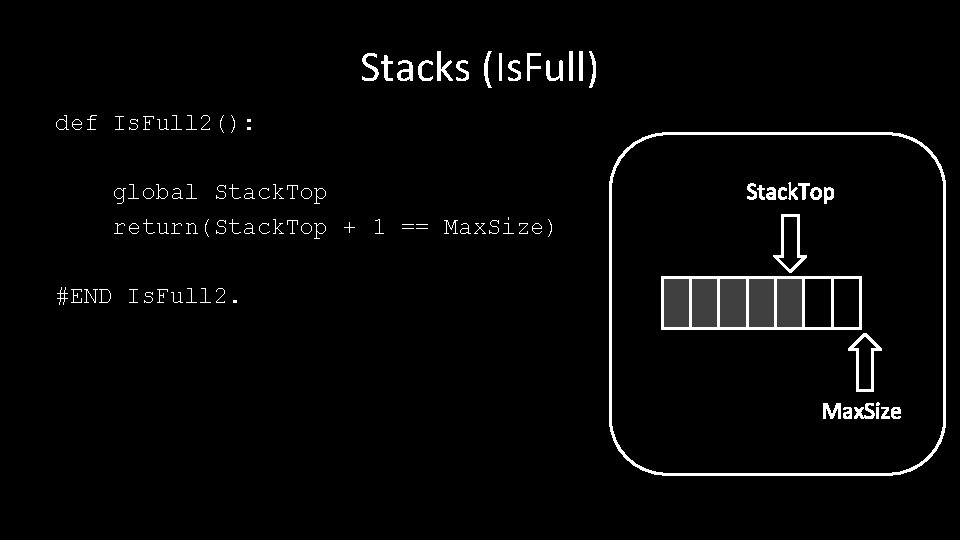
Stacks (Is. Full) def Is. Full 2(): global Stack. Top return(Stack. Top + 1 == Max. Size) Stack. Top #END Is. Full 2. Max. Size

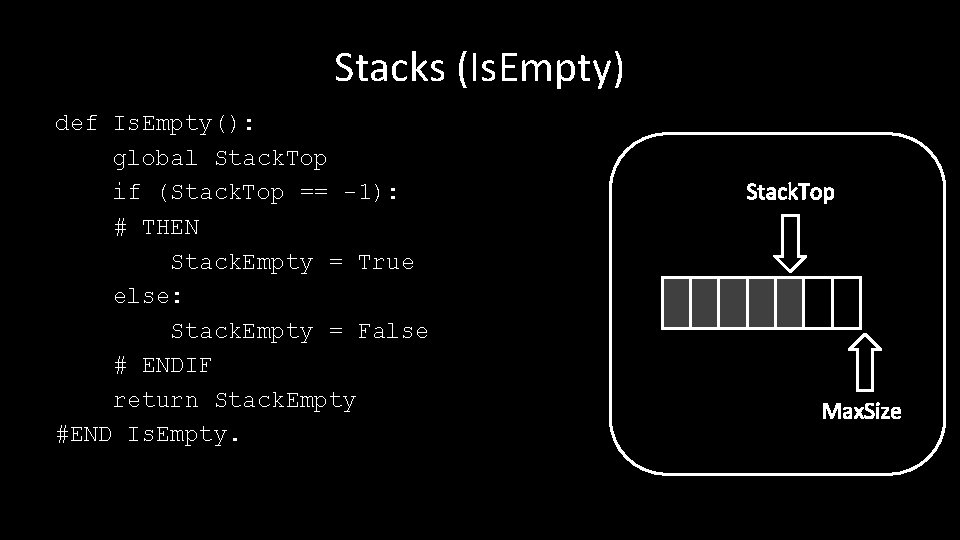
Stacks (Is. Empty) def Is. Empty(): global Stack. Top if (Stack. Top == -1): # THEN Stack. Empty = True else: Stack. Empty = False # ENDIF return Stack. Empty #END Is. Empty. Stack. Top Max. Size

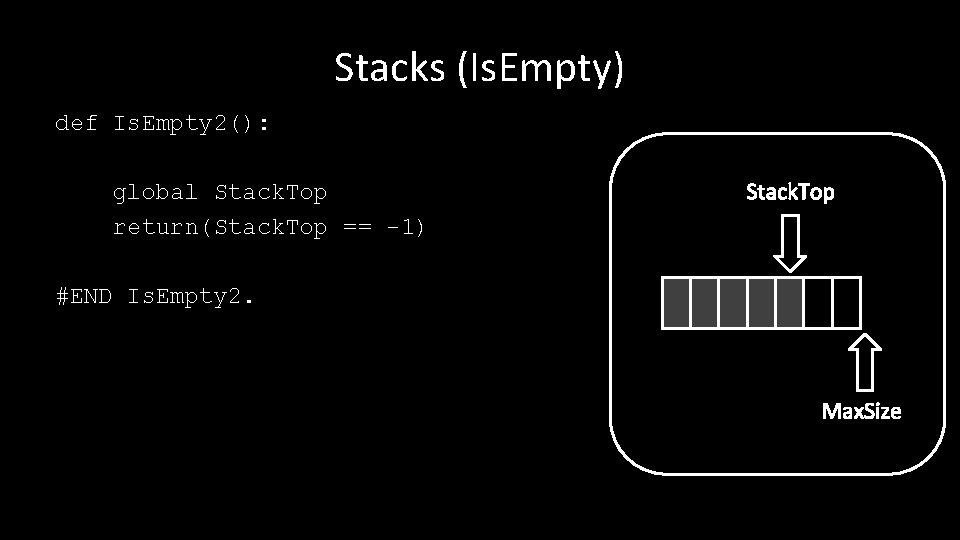
Stacks (Is. Empty) def Is. Empty 2(): global Stack. Top return(Stack. Top == -1) Stack. Top #END Is. Empty 2. Max. Size

Stacks (Push) def Push(N): global Stack. Top if (Is. Full() == True): # THEN print("The stack is full") else: Stack. Top = Stack. Top + 1 Stack[Stack. Top] = N # ENDIF #END Is. Full. Stack. Top Max. Size

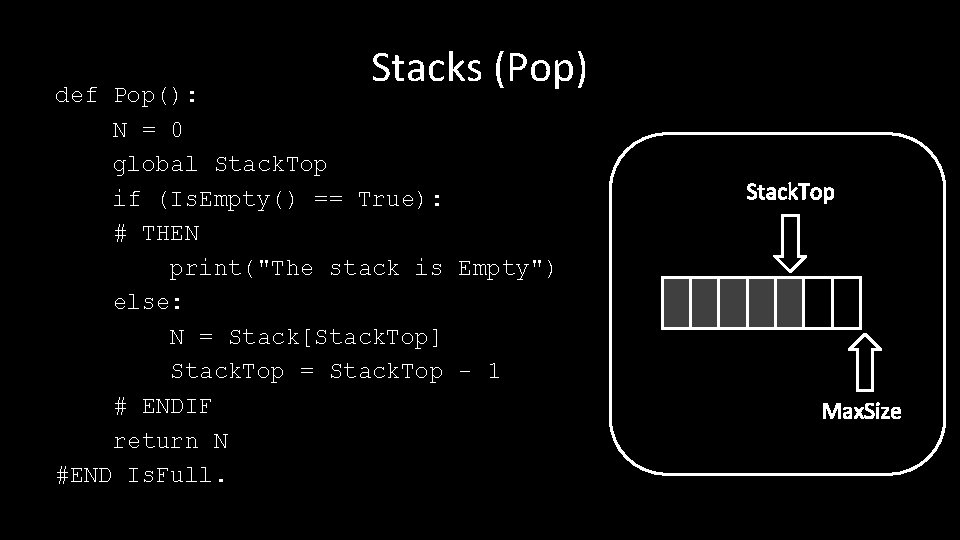
Stacks (Pop) def Pop(): N = 0 global Stack. Top if (Is. Empty() == True): # THEN print("The stack is Empty") else: N = Stack[Stack. Top] Stack. Top = Stack. Top - 1 # ENDIF return N #END Is. Full. Stack. Top Max. Size

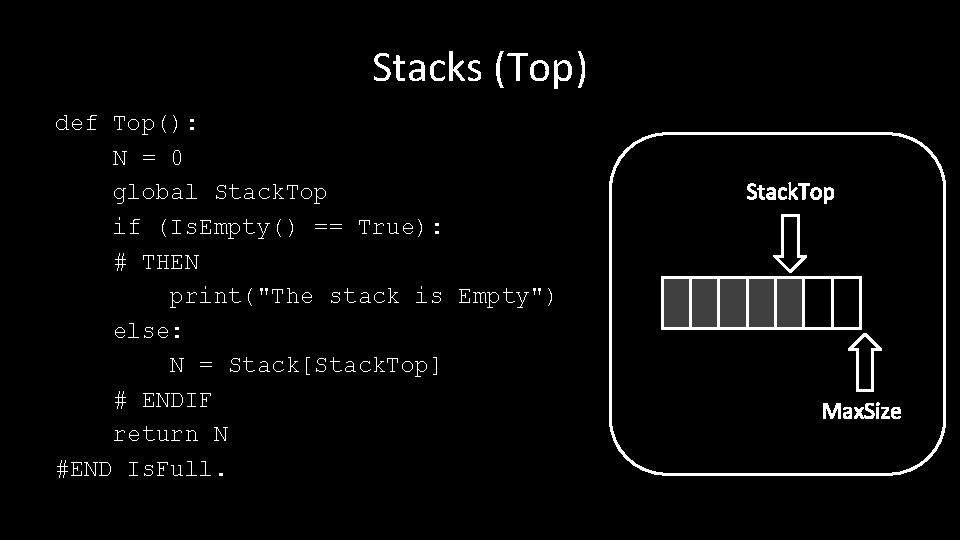
Stacks (Top) def Top(): N = 0 global Stack. Top if (Is. Empty() == True): # THEN print("The stack is Empty") else: N = Stack[Stack. Top] # ENDIF return N #END Is. Full. Stack. Top Max. Size

Queues

Queues • We will remember queues: • It’s a structure that conforms to the principle of First In, First Out (FIFO). • The first item to join the queue is the first item to be served.

Queues • Values are added to the back: 59 86 53 26 59 41 31

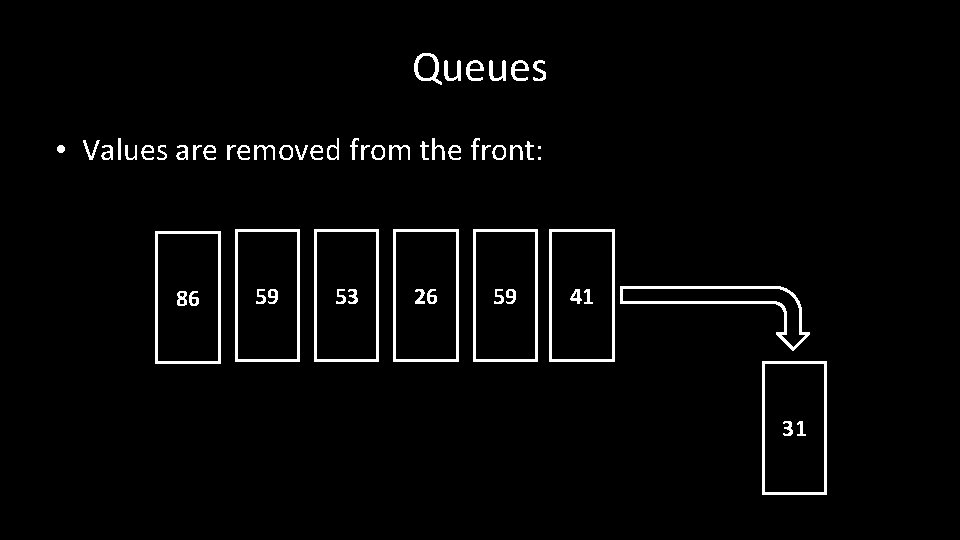
Queues • Values are removed from the front: 86 59 53 26 59 41 31

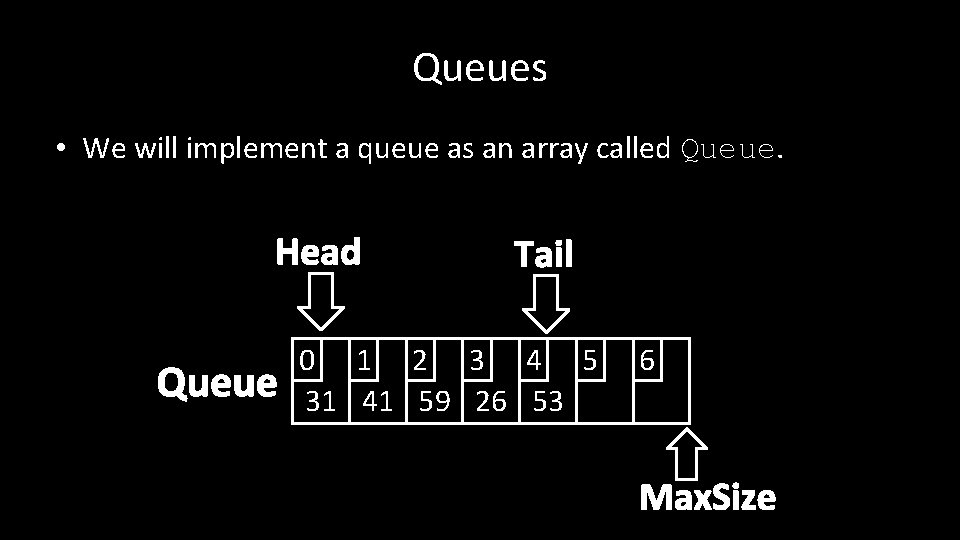
Queues • We will implement a queue as an array called Queue. • The maximum length of the queue is called Max. Size. • The current front of the queue is called Head. • The current back of the queue is called Tail.

Queues • We will implement a queue as an array called Queue. Head Queue Tail 0 1 2 3 4 5 31 41 59 26 53 6 Max. Size

Queues (Declaring) # PROGRAM Queue. As. Array: Queue = [0, 0, 59, 26, 53, 59, 0] Max. Size = 7 Queue. Head = 2 Queue. Tail = 5 #END Queue. As. Array.

Queues • We will look at implementing the following modules: • Is. Full() – Check if the queue is full • Is. Empty() – Check if the queue is full • Add. To. Q(N) – Add a new item (N) to the back of the queue • Delete. From. Q() – Remove the front value from the queue • Clear. Q() – Empty the queue

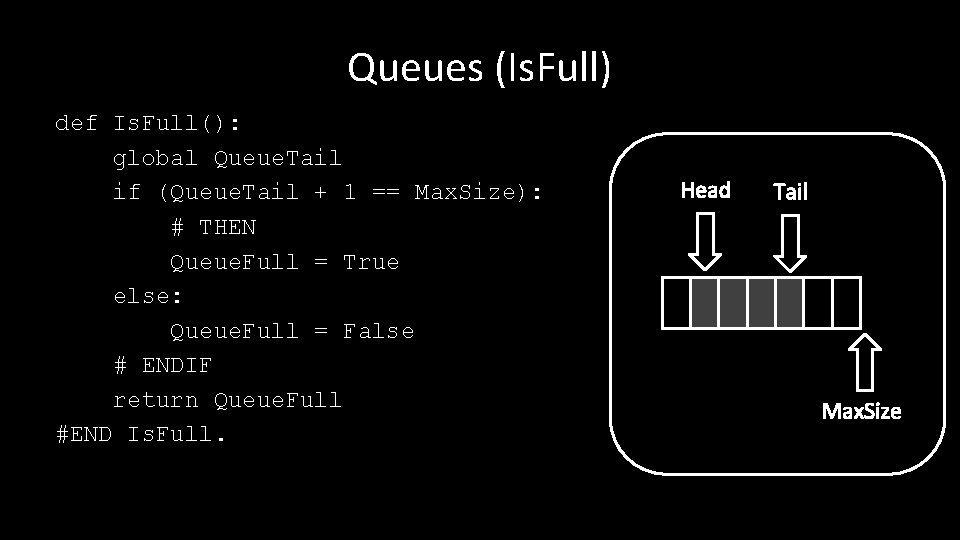
Queues (Is. Full) def Is. Full(): global Queue. Tail if (Queue. Tail + 1 == Max. Size): # THEN Queue. Full = True else: Queue. Full = False # ENDIF return Queue. Full #END Is. Full. Head Tail Max. Size

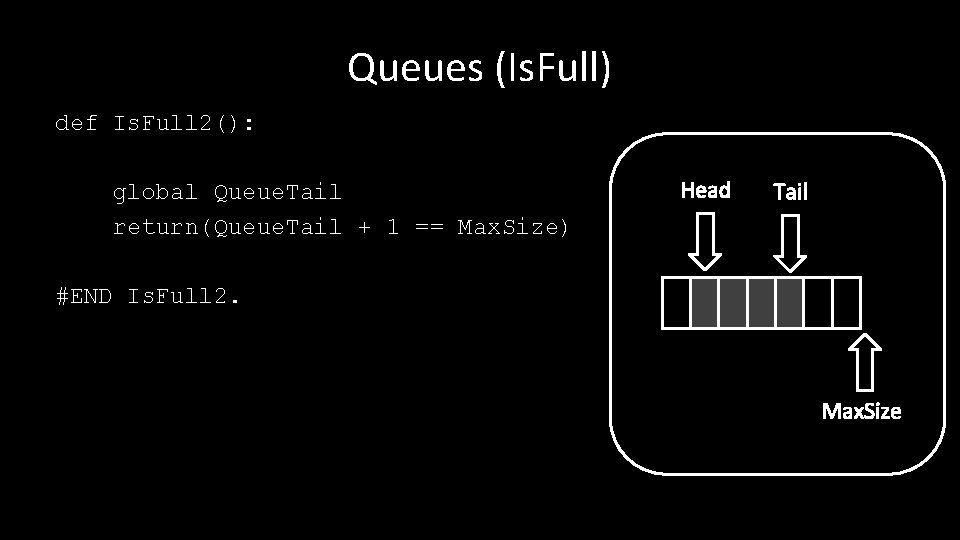
Queues (Is. Full) def Is. Full 2(): global Queue. Tail return(Queue. Tail + 1 == Max. Size) Head Tail #END Is. Full 2. Max. Size

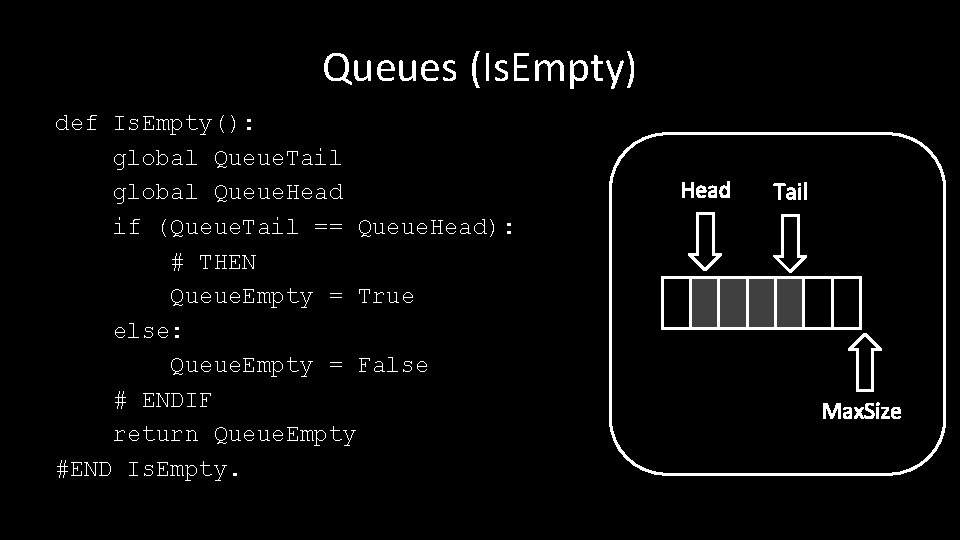
Queues (Is. Empty) def Is. Empty(): global Queue. Tail global Queue. Head if (Queue. Tail == Queue. Head): # THEN Queue. Empty = True else: Queue. Empty = False # ENDIF return Queue. Empty #END Is. Empty. Head Tail Max. Size

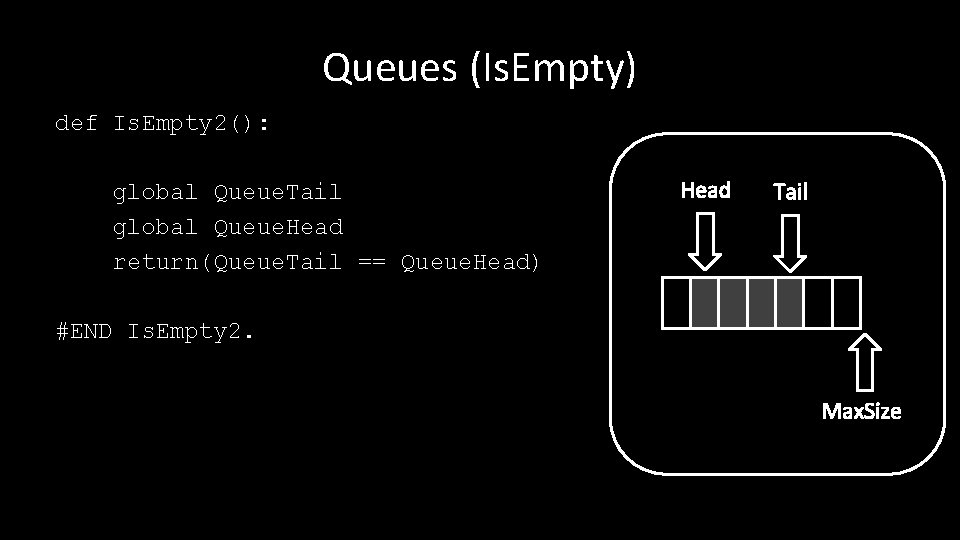
Queues (Is. Empty) def Is. Empty 2(): global Queue. Tail global Queue. Head return(Queue. Tail == Queue. Head) Head Tail #END Is. Empty 2. Max. Size

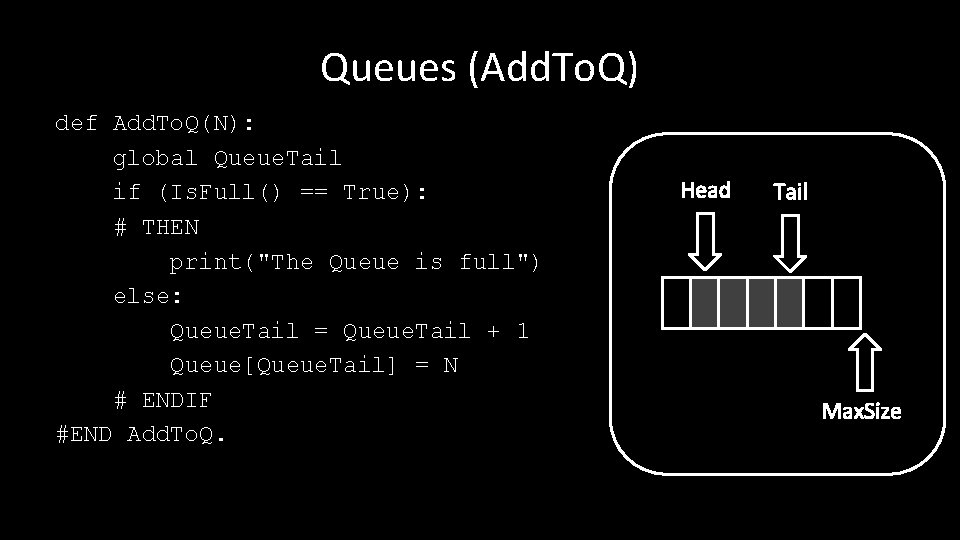
Queues (Add. To. Q) def Add. To. Q(N): global Queue. Tail if (Is. Full() == True): # THEN print("The Queue is full") else: Queue. Tail = Queue. Tail + 1 Queue[Queue. Tail] = N # ENDIF #END Add. To. Q. Head Tail Max. Size

Queues (Delete. From. Q) def Delete. From. Q(): N = 0 global Queue. Head if (Is. Empty() == True): # THEN print("The Queue is Empty") else: N = Queue[Queue. Head] Queue. Head = Queue. Head + 1 # ENDIF return N #END Delete. From. Q. Head Tail Max. Size

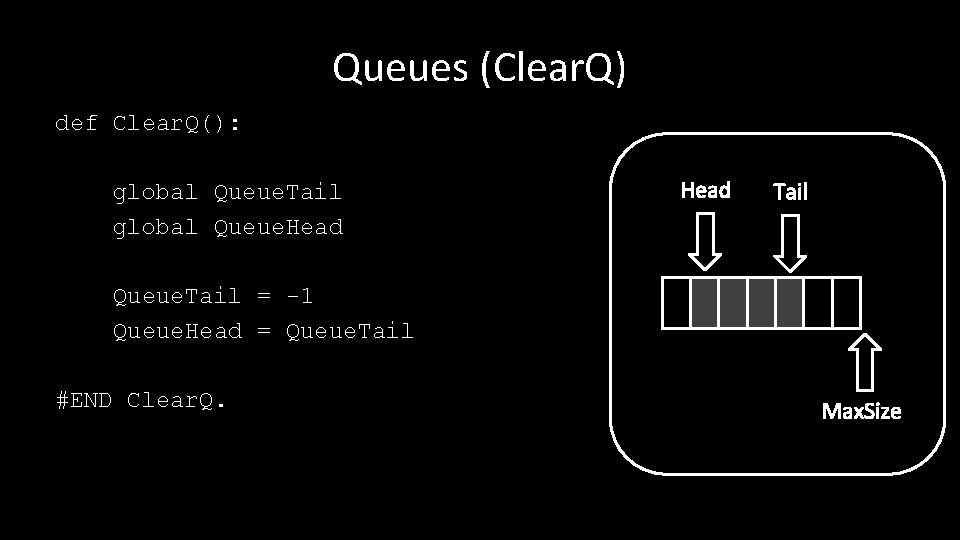
Queues (Clear. Q) def Clear. Q(): global Queue. Tail global Queue. Head Tail Queue. Tail = -1 Queue. Head = Queue. Tail #END Clear. Q. Max. Size

Circular Queues

Circular Queues Head 7 • We can also have a circular queue: 43 6 • A queue where the start and end of the queue are joined together. 0 12 35 5 Tail 22 4 99 3 1 2

Circular Queues • So Tail starts at 4, goes to 5, goes to 6, goes to 0, goes to 1, etc. • So it’s Tail = Tail + 1, • But… • Tail = (Tail + 1) % 7 • • • So Tail % Max. Size works as follows: 4 % Max. Size = 4 5 % Max. Size = 5 6 % Max. Size = 6 7 % Max. Size = 0 8 % Max. Size = 1

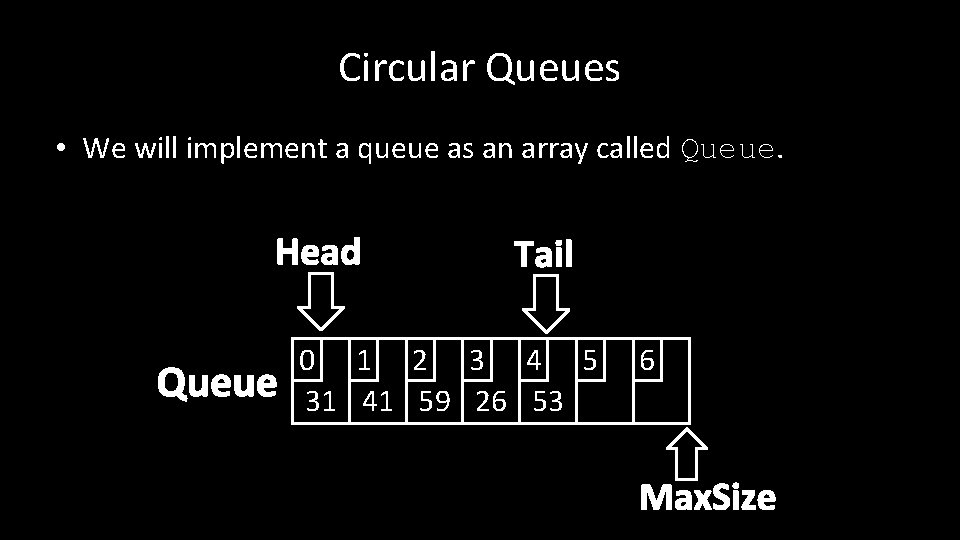
Circular Queues • We will implement a queue as an array called Queue. • The maximum length of the queue is called Max. Size. • The current front of the queue is called Head. • The current back of the queue is called Tail.

Circular Queues • We will implement a queue as an array called Queue. Head Queue Tail 0 1 2 3 4 5 31 41 59 26 53 6 Max. Size

Circular Queues (Declaring) # PROGRAM CQueue. As. Array: Queue = [0, 0, 59, 26, 53, 59, 0] Max. Size = 7 Queue. Head = 2 Queue. Tail = 5 #END CQueue. As. Array.

Circular Queues • We will look at implementing the following modules: • Is. Full() – Check if the queue is full • Is. Empty() – Check if the queue is full • Add. To. Q(N) – Add a new item (N) to the back of the queue • Delete. From. Q() – Remove the front value from the queue • Clear. Q() – Empty the queue

Circular Queues (Is. Full) def Is. Full(): global Queue. Tail global Max. Size if (Queue. Head == (Queue. Tail + 1) % Max. Size): # THEN Queue. Full = True else: 6 Queue. Full = False # ENDIF return Queue. Full #END Is. Full. 7 0 43 12 35 5 22 4 99 3 1 2

def Is. Full 2(): Circular Queues (Is. Full) global Queue. Tail return(Queue. Head == (Queue. Tail + 1) % Max. Size) 7 #END Is. Full 2. 0 43 6 12 35 5 22 4 99 3 1 2

Circular Queues (Is. Empty) def Is. Empty(): global Queue. Tail global Queue. Head if (Queue. Tail == Queue. Head): # THEN Queue. Empty = True else: Queue. Empty = False # ENDIF return Queue. Empty #END Is. Empty. 7 0 43 6 12 35 5 22 4 99 3 1 2

Circular Queues (Is. Empty) def Is. Empty 2(): global Queue. Tail global Queue. Head return(Queue. Tail == Queue. Head) #END Is. Empty 2. 7 0 43 6 12 35 5 22 4 99 3 1 2

Circular Queues (Add. To. Q) def Add. To. Q(N): global Queue. Tail global Max. Size if (Is. Full() == True): # THEN print("The Queue is full") else: Queue. Tail = (Queue. Tail + 1) % Max. Size Queue[Queue. Tail] = N # ENDIF #END Add. To. Q. 7 0 43 6 12 35 5 22 4 99 3 1 2

Circular Queues (Delete. From. Q) def Delete. From. Q(): global Queue. Head global Max. Size N = 0 if (Is. Empty() == True): # THEN print("The Queue is Empty") else: N = Queue[Queue. Head] Queue. Head = (Queue. Head + 1) % Max. Size # ENDIF return N #END Delete. From. Q. 7 0 43 6 12 35 5 22 4 99 3 1 2

Circular Queues (Clear. Q) def Clear. Q(): global Queue. Tail global Queue. Head Queue. Tail = -1 Queue. Head = Queue. Tail #END Clear. Q. 7 0 43 6 12 35 5 22 4 99 3 1 2

etc.