PESQUISA OPERACIONAL PARA A ENGENHARIA DE PRODUO II

PESQUISA OPERACIONAL PARA A ENGENHARIA DE PRODUÇÃO II **Aula Básica de GAMS** Profa. Vitória Pureza 1º Semestre Aulas 5 e 6

Roteiro • Implementação passo a passo de um modelo de programação matemática • Alguns detalhes de implementação Brook, Kendrick & Meeraus (1992)

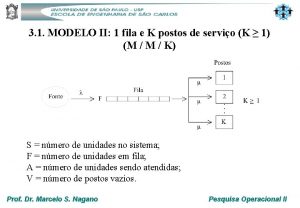
Um Modelo de Transporte Min 132 x 11 + 87 x 12 + 97 x 13 + 103 x 14 + 85 x 21 + 91 x 22 + 19 x 23 + 215 x 24 + 106 x 31 + 89 x 32 + 100 x 33 + 98 x 34 sujeito a: x 11 + x 12 + x 13 + x 14 ≤ 135 x 21 + x 22 + x 23 + x 24 ≤ 56 Restrições de suprimento x 31 + x 32 + x 33 + x 34 ≤ 93 x 11 + x 21 + x 31 ≥ 62 x 12 + x 22 + x 32 ≥ 83 Restrições de demanda x 13 + x 23 + x 33 ≥ 39 x 14 + x 24 + x 34 ≥ 91 xij ≥ 0 i=1, 2, 3; j=1, 2, 3, 4 Restrições de sinal Variáveis de decisão: xij= unidades de produto enviados da fábrica i ao cliente j

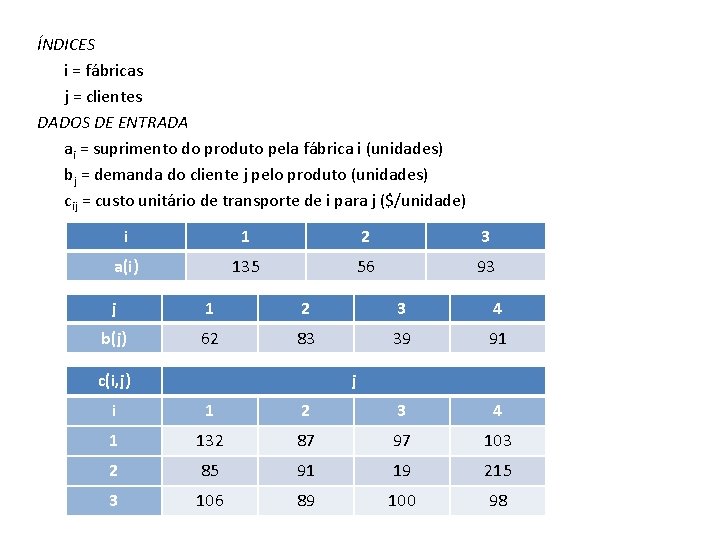
ÍNDICES i = fábricas j = clientes DADOS DE ENTRADA ai = suprimento do produto pela fábrica i (unidades) bj = demanda do cliente j pelo produto (unidades) cij = custo unitário de transporte de i para j ($/unidade) i 1 2 3 a(i) 135 56 93 j 1 2 3 4 b(j) 62 83 39 91 c(i, j) j i 1 2 3 4 1 132 87 97 103 2 85 91 19 215 3 106 89 100 98

Variáveis de decisão xij= unidades de produtos produzidos pela fábrica i e enviados ao cliente j onde xij ≥ 0, i=1. . 3, j=1. . 4. Restrições Capacidade da fábrica i: Demanda do cliente j: Função objetivo

Sets i fabricas /fab 1, fab 2, fab 3/ j clientes /cli 1, cli 2, cli 3, cli 4/; Parameter a(i) capacidade da fabrica i /fab 1 135 fab 2 56 fab 3 93/ b(j) demanda do cliente j /cli 1 62 cli 2 83 cli 3 39 cli 4 91/; Table c(i, j) custos unitarios de suprimento do cliente j pela fabrica i cli 1 cli 2 cli 3 cli 4 fab 1 132 87 97 103 fab 2 85 91 19 215 fab 3 106 89 100 98; Variables x(i, j) quantidade de produto enviado pela fabrica i para o cliente j z custo total em $; Positive variable x; Equations custo funcao objetivo capacidade(i) limite de capacidade da fabrica i demanda(j) necessidade de suprimento do cliente j; custo. . z =e= sum((i, j), c(i, j)*x(i, j)); capacidade(i). . sum(j, x(i, j)) =l= a(i); demanda(j). . sum(i, x(i, j)) =g= b(j); model transp 1 /all/; solve transp 1 using lp minimizing z; display x. l, x. m; IMPLEMENTAÇÃO EM GAMS DO MODELO DE TRANSPORTE MÉTODO x*=(x 11*, x 12*, . . . , x 34*)

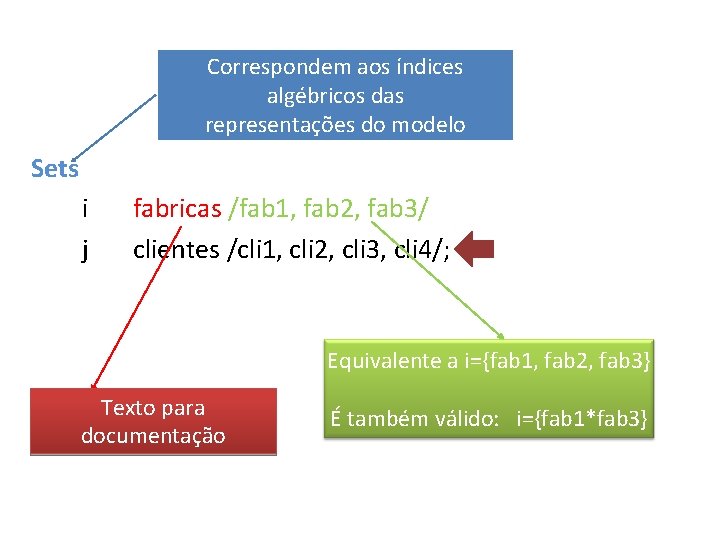
Correspondem aos índices algébricos das representações do modelo Sets i j fabricas /fab 1, fab 2, fab 3/ clientes /cli 1, cli 2, cli 3, cli 4/; Equivalente a i={fab 1, fab 2, fab 3} Texto para documentação É também válido: i={fab 1*fab 3}

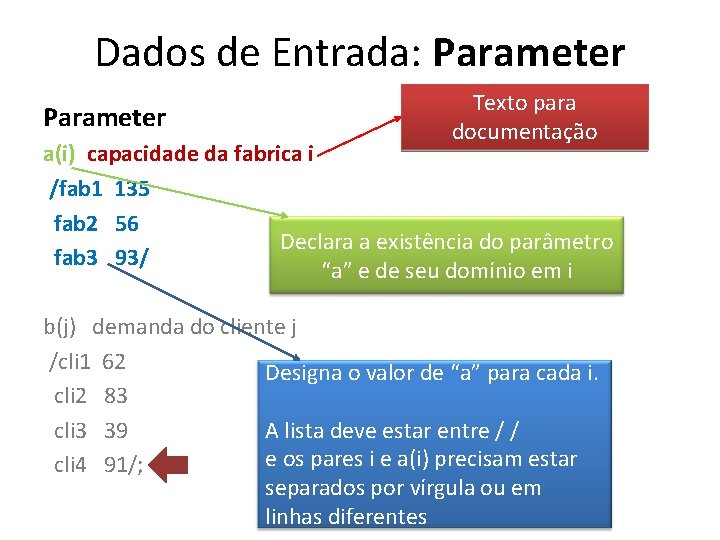
Dados de Entrada: Parameter Texto para documentação a(i) capacidade da fabrica i /fab 1 135 fab 2 56 Declara a existência do parâmetro fab 3 93/ “a” e de seu domínio em i b(j) demanda do cliente j /cli 1 62 Designa o valor de “a” para cada i. cli 2 83 A lista deve estar entre / / cli 3 39 e os pares i e a(i) precisam estar cli 4 91/; separados por vírgula ou em linhas diferentes

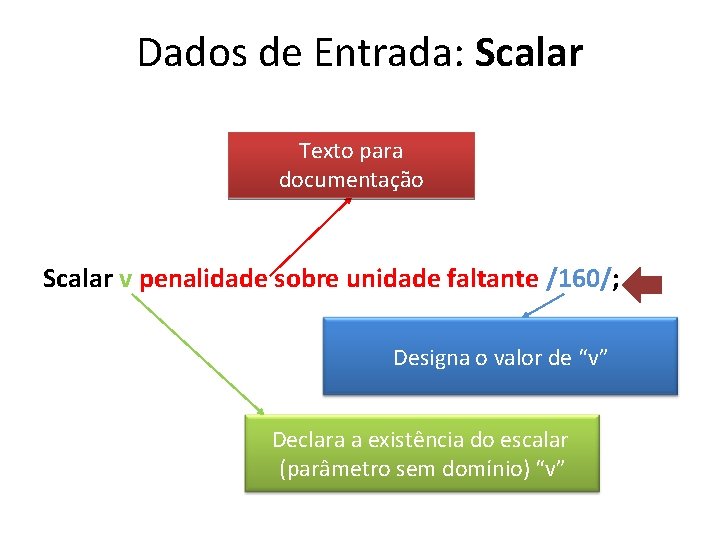
Dados de Entrada: Scalar Texto para documentação Scalar v penalidade sobre unidade faltante /160/; Designa o valor de “v” Declara a existência do escalar (parâmetro sem domínio) “v”

Dados de Entrada: Table Declara a existência da tabela “c” e seu domínio em i e j Texto para documentação Table c(i, j) custos unitarios de suprimento do cliente j pela fabrica i cli 1 cli 2 cli 3 cli 4 fab 1 132 87 97 103 fab 2 85 91 19 215 fab 3 106 89 100 98; Designa o valor de “c” a cada i (linha) e j (coluna)

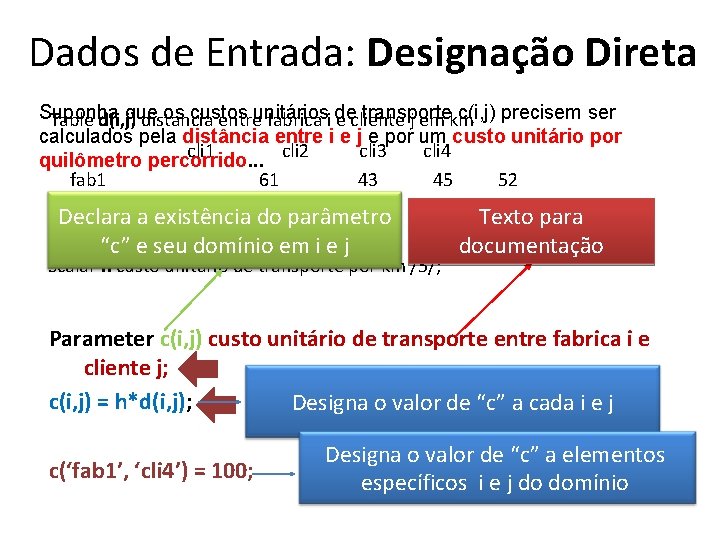
Dados de Entrada: Designação Direta Suponha que os custos transporte c(i, j) precisem ser Table d(i, j) distancia entreunitários fabrica i de e cliente j em km calculados pela distância entre i e j e por um custo unitário por cli 1 cli 2 cli 3 cli 4 quilômetro percorrido. . . fab 1 61 43 45 52 fab 2 43 9 106 Texto para Declara a existência do 47 parâmetro fab 3“c” e seu 53 45 i e j 50 46; documentação domínio em Scalar h custo unitário de transporte por km /5/; Parameter c(i, j) custo unitário de transporte entre fabrica i e cliente j; c(i, j) = h*d(i, j); Designa o valor de “c” a cada i e j c(‘fab 1’, ‘cli 4’) = 100; Designa o valor de “c” a elementos específicos i e j do domínio

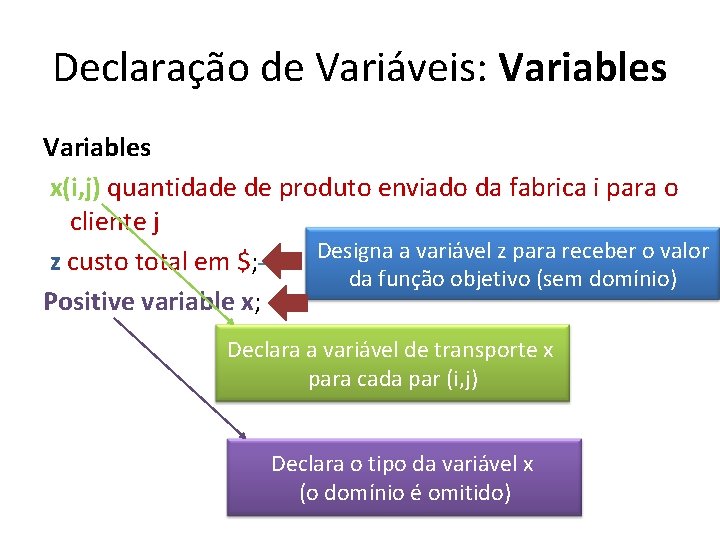
Declaração de Variáveis: Variables x(i, j) quantidade de produto enviado da fabrica i para o cliente j Designa a variável z para receber o valor z custo total em $; da função objetivo (sem domínio) Positive variable x; Declara a variável de transporte x para cada par (i, j) Declara o tipo da variável x (o domínio é omitido)

Tipos de Variáveis TIPO DOMÍNIO FREE [- , + ] POSITIVE [0, + ] NEGATIVE [- , 0] BINARY {0, 1} INTEGER {0, 1, . . . , 100} • A variável z que recebe o valor da fo (quantidade a ser otimizada) é do tipo free • A declaração para variáveis do tipo free pode ser omitida

Declaração da Fo e Restrições: Equations custo funcao objetivo capacidade(i) limite de capacidade da fabrica i demanda(j) necessidade de suprimento do cliente j; Declara o nome da função objetivo (custo ) - sem domínio Declara o nome das restrições (capacidade e demanda) e seus domínios

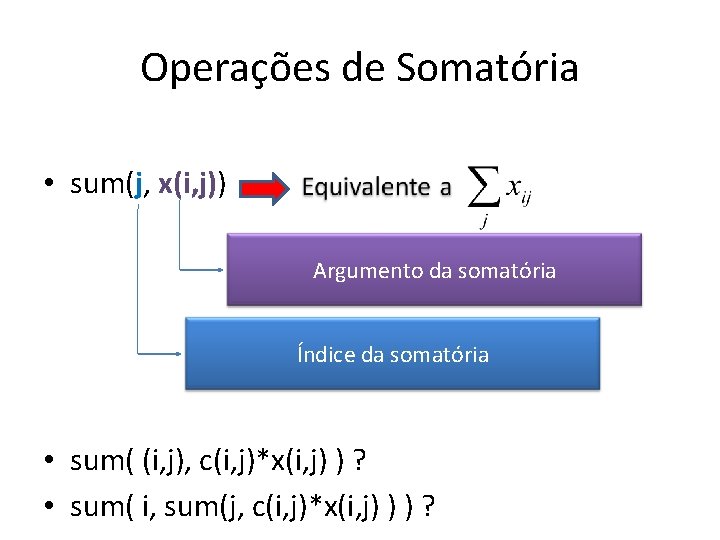
Operações de Somatória • sum(j, x(i, j)) Argumento da somatória Índice da somatória • sum( (i, j), c(i, j)*x(i, j) ) ? • sum( i, sum(j, c(i, j)*x(i, j) ) ) ?

Operador Condicional ($) • sum( (i) $ (ORD(i) le 4), x(i) ) Operador condicional: limita o domínio de i na operação para os valores que satisfazem a condição que se segue Significa: “Se a ordem de i for menor ou igual a 4”. Ou seja, considera apenas os termos x(i) dos 4 primeiros “i” na somatória

Operador Alias Set i fabricas /fab 1, fab 2, fab 3/ Alias (i, j); Cria um set j com os mesmos elementos do set i. Ou seja, Set j fabricas /fab 1, fab 2, fab 3/)

Designação de Equations custo. . z =e= sum((i, j), c(i, j)*x(i, j)); capacidade(i). . sum(j, x(i, j)) =l= a(i); demanda(j). . sum(i, x(i, j)) =g= b(j); Operadores relacionais Nome e domínio da equation seguido de “. . ” e um espaço

Observações Importantes • Para cada um dos três elementos do domínio i temos uma desigualdade “capacidade” • Para cada um dos quatro elementos do domínio j temos uma desigualdade “demanda” Ou seja, com apenas duas linhas, são criadas 3+4 desigualdades

Observações Importantes OPERADORES RELACIONAIS =l= ≤ =g= ≥ =e= = • O operador “=“ é usado em designações diretas e o operador “=e=“ é usado na designação de equations • Uma designação direta dá o valor desejado ao parâmetro ANTES do problema ser resolvido • Uma designação de equation descreve uma relação desejada mas que só pode ser satisfeita DEPOIS do problema ser resolvido

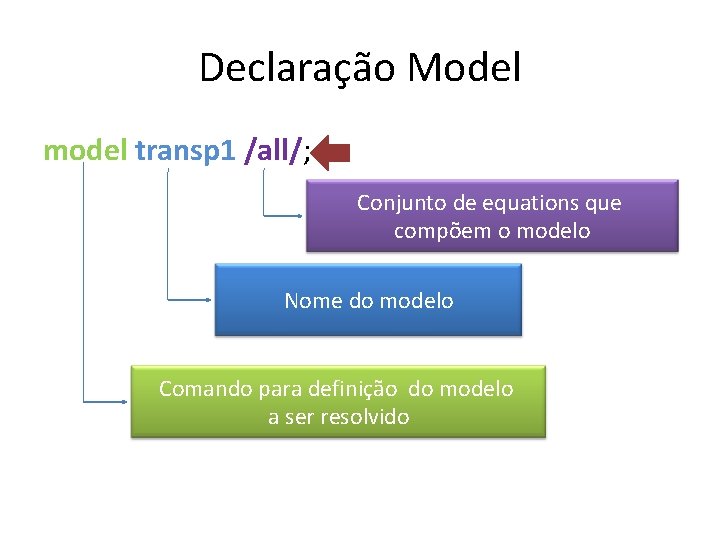
Declaração Model model transp 1 /all/; Conjunto de equations que compõem o modelo Nome do modelo Comando para definição do modelo a ser resolvido

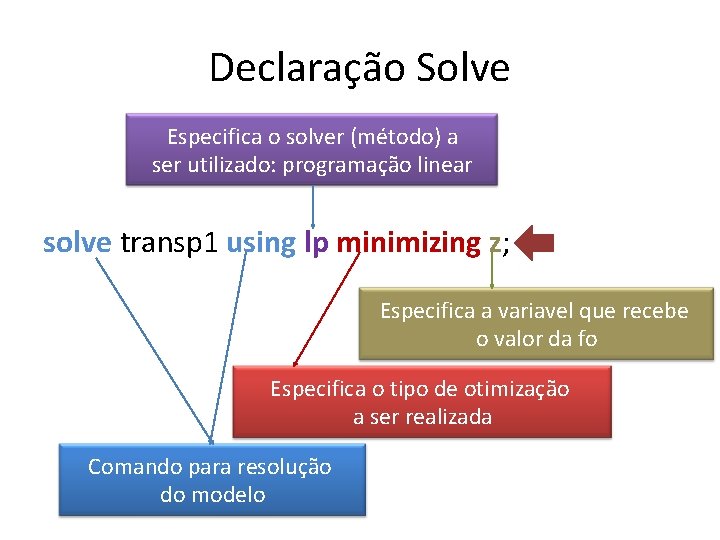
Declaração Solve Especifica o solver (método) a ser utilizado: programação linear solve transp 1 using lp minimizing z; Especifica a variavel que recebe o valor da fo Especifica o tipo de otimização a ser realizada Comando para resolução do modelo

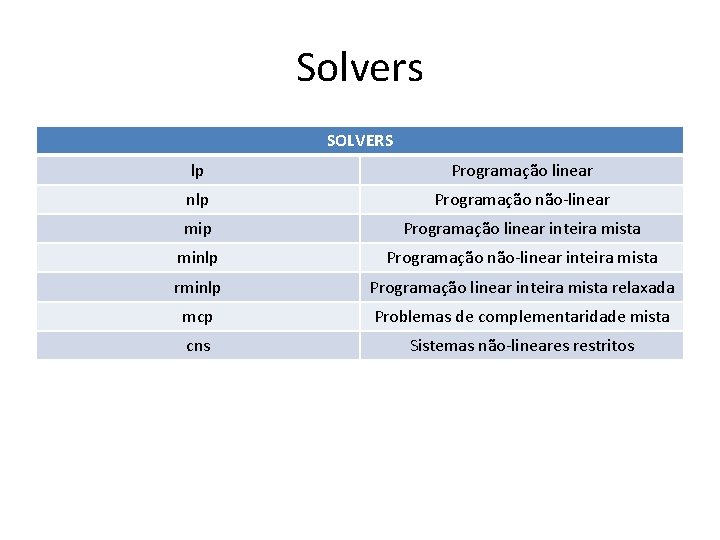
Solvers SOLVERS lp Programação linear nlp Programação não-linear mip Programação linear inteira mista minlp Programação não-linear inteira mista rminlp Programação linear inteira mista relaxada mcp Problemas de complementaridade mista cns Sistemas não-lineares restritos

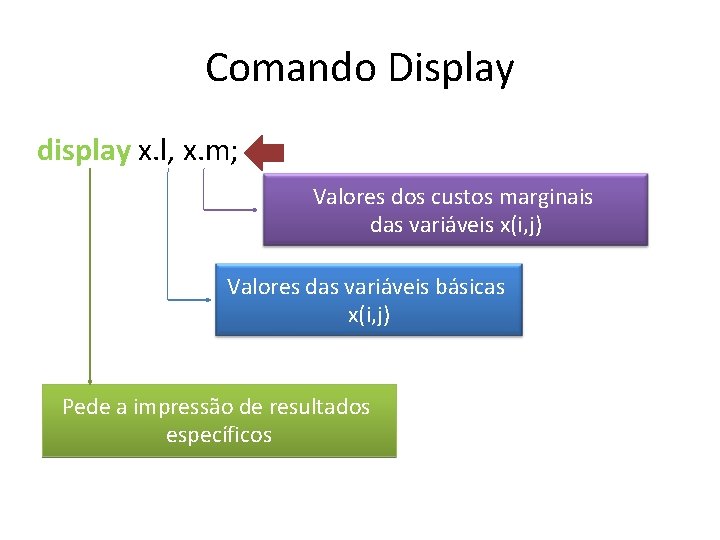
Comando Display display x. l, x. m; Valores dos custos marginais das variáveis x(i, j) Valores das variáveis básicas x(i, j) Pede a impressão de resultados específicos

Listagem ---- 41 VARIABLE x. L quantidade de produto enviado pela fabrica i para o cliente j cli 1 cli 2 cli 3 cli 4 fab 1 83. 000 43. 000 fab 2 17. 000 39. 000 fab 3 45. 000 48. 000 ---- 41 VARIABLE x. M quantidade de produto enviado pela fabrica i para o cliente j cli 1 cli 2 cli 3 cli 4 fab 1 21. 000 52. 000 fab 2 30. 000 138. 000 fab 3 7. 000 60. 000

Exercícios 1. Implemente e resolva os exercícios da lista 2. No exercício 2 da lista 2, resolva o modelo do lucro total das duas fábricas.

2. Implemente e resolva o exemplo de problema multi -período da aula 4 (produção de barcos). 3. Para o exemplo do exercício 2, considere que a reavaliação da demanda e do planejamento ocorra a cada 2 trimestres. Simule o planejamento com horizonte rolante por 3 avaliações (a cada avaliação, um modelo GAMS deve ser resolvido).

Variáveis de Decisão: xt = número de barcos produzidos no trimestre t em horas regulares ( t=1. . 4) yt = número de barcos produzidos no trimestre t em horas extras ( t=1. . 4) It = número de barcos em estoque no trimestre t ( t=1. . 4) sujeito a: xt ≤ 40 It-1 + xt + yt = dt + It I 0 = 10 xt , y t , I t ≥ 0 t=1. . 4 (capacidade de produção com horas regulares) (balanço de estoque) (estoque inicial) (sinal)