Ordinary Differential Equation The methods for Initial Value

Ordinary Differential Equation ü The methods for Initial Value Problems (IVPs): ü Multi-step Methods

ESO 208 A: Computational Methods in Engineering Ordinary Differential Equation: System of IVPs and

Stability of the System of IVPs ü In higher order IVP or in a

Stability: BDF Methods Example ü For all the BDFs: Stability Region is outside the

Method h BDF 1 0. 01 0. 05 0. 1 0. 2 0. 4

Method h BDF 1 0. 02 0. 04 0. 08 0. 16 0. 32

ESO 208 A: Computational Methods in Engineering Partial Differential Equations: Introduction, Parabolic Equation Department

Slides: 36

Download presentation

Ordinary Differential Equation ü The methods for Initial Value Problems (IVPs): ü Multi-step Methods ü Explicit: Euler Forward, Adams-Bashforth ü Implicit: Euler Backward, Trapezoidal and Adams-Moulton ü Backward Difference Formulae (BDF) ü Runge-Kutta Methods ü Applications, Startup, Combination Methods (Predictor. Corrector) ü Consistency, Stability, Convergence ü Application to System of ODEs ü Boundary Value Problems (BVPs) ü Shooting Method ü Direct Methods

ESO 208 A: Computational Methods in Engineering Ordinary Differential Equation: System of IVPs and Higher Order IVPs Abhas Singh Department of Civil Engineering IIT Kanpur Acknowledgements: Profs. Saumyen Guha and Shivam Tripathi (CE)

System of IVPs •

Higher Order IVP •

Higher Order IVP: Example •

Numerical Methods for System of IVPs •

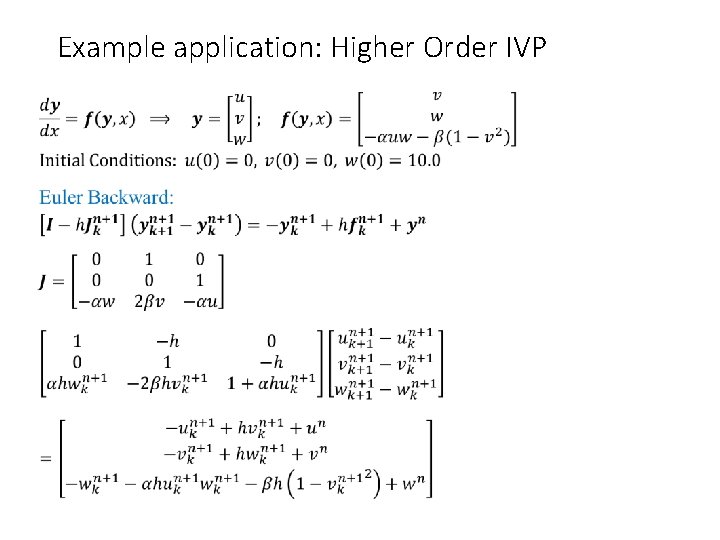
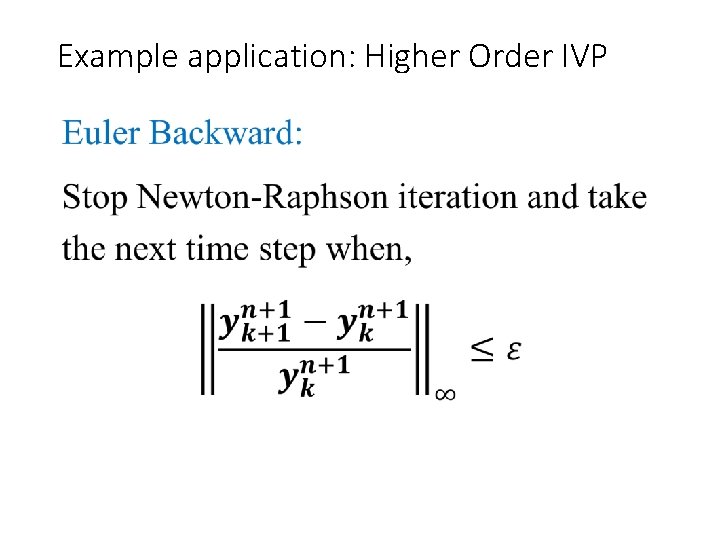
Example application: Higher Order IVP •

Stability of the System of IVPs •

Stability of the System of IVPs ü In higher order IVP or in a system of IVP, the solutions are characterized by the eigenvalues. ü One or two equation in the system typically have high eigenvalues close to λmax and the rest of the equations may have eigenvalues of much lower magnitudes! ü The time step is restricted by λmax. ü Stiff system: large value of (λmax/λmin); typically > 100 ü As the time progresses, larger time step can be used for the problem but is limited by the stability criteria! ü This is the utility of the BDFs: ü They are stable for all real and negative λR up to 6 th order ü Region of stability for imaginary λI increases as one increases the time step (increasing λRh)!

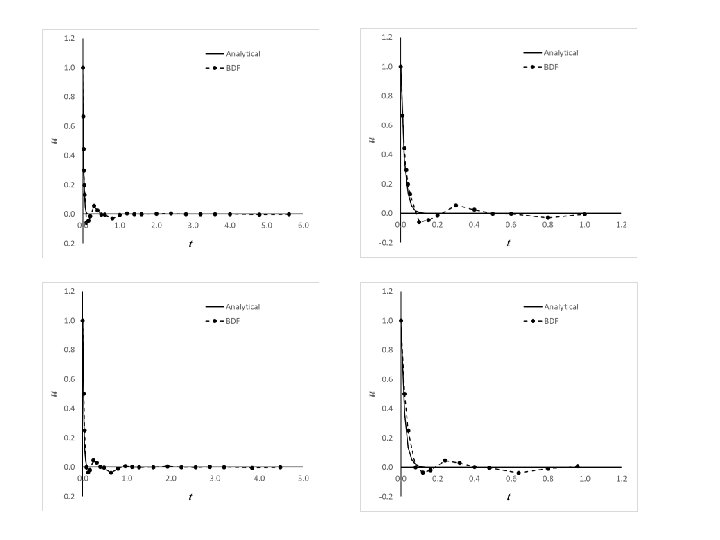
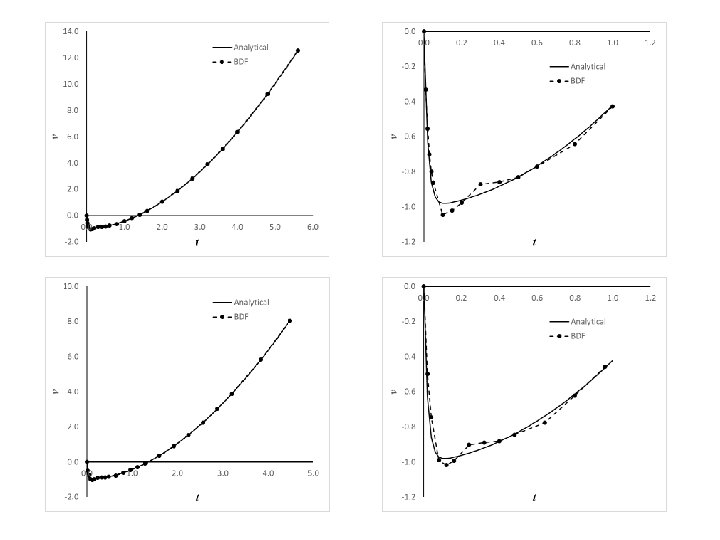
Example: Stiff System •

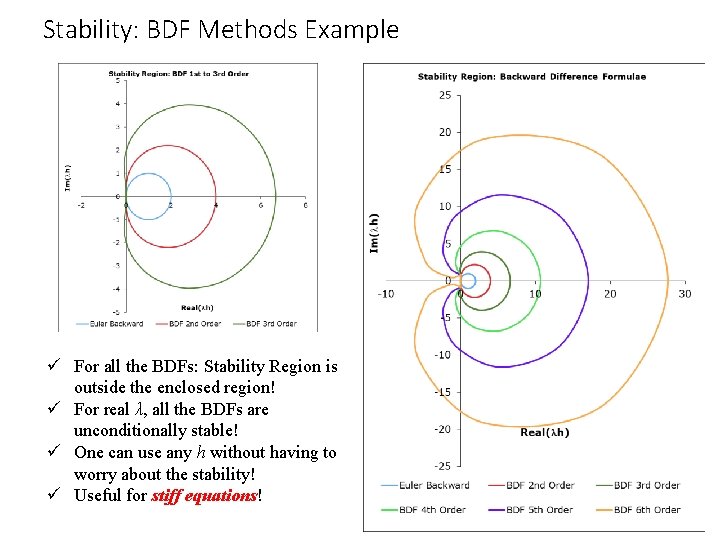
Stability: BDF Methods Example ü For all the BDFs: Stability Region is outside the enclosed region! ü For real λ, all the BDFs are unconditionally stable! ü One can use any h without having to worry about the stability! ü Useful for stiff equations!

Stability of the System of IVPs •

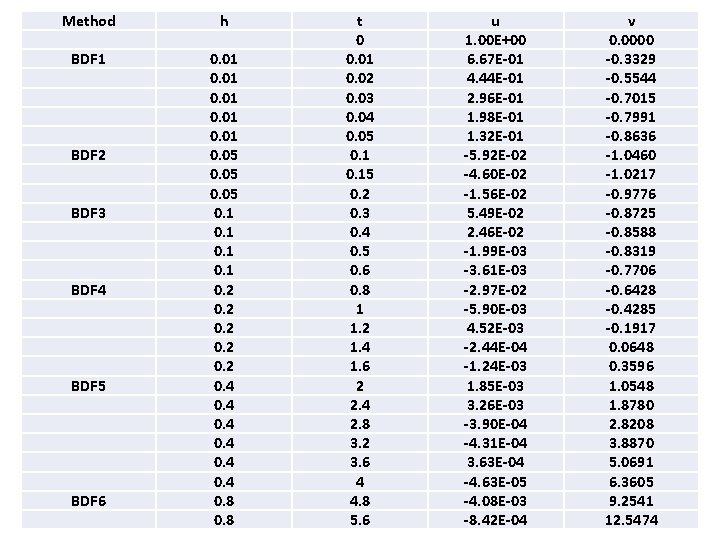
Method h BDF 1 0. 01 0. 05 0. 1 0. 2 0. 4 0. 8 BDF 2 BDF 3 BDF 4 BDF 5 BDF 6 t 0 0. 01 0. 02 0. 03 0. 04 0. 05 0. 15 0. 2 0. 3 0. 4 0. 5 0. 6 0. 8 1 1. 2 1. 4 1. 6 2 2. 4 2. 8 3. 2 3. 6 4 4. 8 5. 6 u 1. 00 E+00 6. 67 E-01 4. 44 E-01 2. 96 E-01 1. 98 E-01 1. 32 E-01 -5. 92 E-02 -4. 60 E-02 -1. 56 E-02 5. 49 E-02 2. 46 E-02 -1. 99 E-03 -3. 61 E-03 -2. 97 E-02 -5. 90 E-03 4. 52 E-03 -2. 44 E-04 -1. 24 E-03 1. 85 E-03 3. 26 E-03 -3. 90 E-04 -4. 31 E-04 3. 63 E-04 -4. 63 E-05 -4. 08 E-03 -8. 42 E-04 v 0. 0000 -0. 3329 -0. 5544 -0. 7015 -0. 7991 -0. 8636 -1. 0460 -1. 0217 -0. 9776 -0. 8725 -0. 8588 -0. 8319 -0. 7706 -0. 6428 -0. 4285 -0. 1917 0. 0648 0. 3596 1. 0548 1. 8780 2. 8208 3. 8870 5. 0691 6. 3605 9. 2541 12. 5474

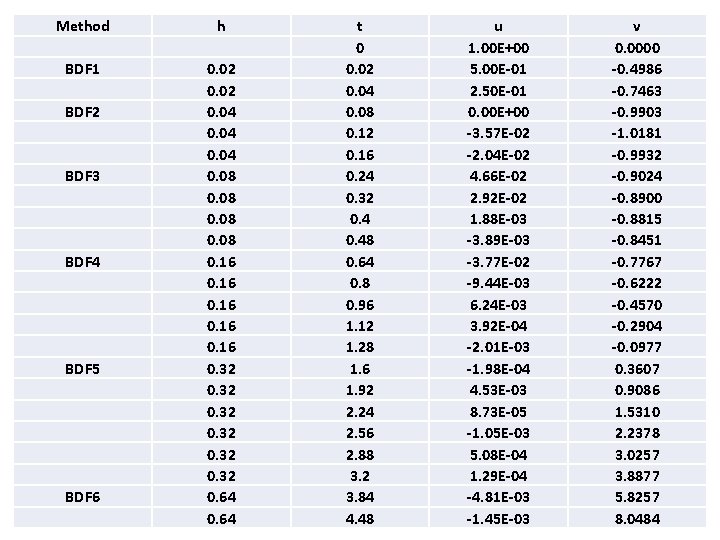
Method h BDF 1 0. 02 0. 04 0. 08 0. 16 0. 32 0. 64 BDF 2 BDF 3 BDF 4 BDF 5 BDF 6 t 0 0. 02 0. 04 0. 08 0. 12 0. 16 0. 24 0. 32 0. 48 0. 64 0. 8 0. 96 1. 12 1. 28 1. 6 1. 92 2. 24 2. 56 2. 88 3. 2 3. 84 4. 48 u 1. 00 E+00 5. 00 E-01 2. 50 E-01 0. 00 E+00 -3. 57 E-02 -2. 04 E-02 4. 66 E-02 2. 92 E-02 1. 88 E-03 -3. 89 E-03 -3. 77 E-02 -9. 44 E-03 6. 24 E-03 3. 92 E-04 -2. 01 E-03 -1. 98 E-04 4. 53 E-03 8. 73 E-05 -1. 05 E-03 5. 08 E-04 1. 29 E-04 -4. 81 E-03 -1. 45 E-03 v 0. 0000 -0. 4986 -0. 7463 -0. 9903 -1. 0181 -0. 9932 -0. 9024 -0. 8900 -0. 8815 -0. 8451 -0. 7767 -0. 6222 -0. 4570 -0. 2904 -0. 0977 0. 3607 0. 9086 1. 5310 2. 2378 3. 0257 3. 8877 5. 8257 8. 0484

ESO 208 A: Computational Methods in Engineering Partial Differential Equations: Introduction, Parabolic Equation Department of Civil Engineering IIT Kanpur

Introduction •

Parabolic PDE: semi-discretization •