PART 7 Ordinary Differential Equations ODEs Ordinary Differential

PART 7 Ordinary Differential Equations ODEs

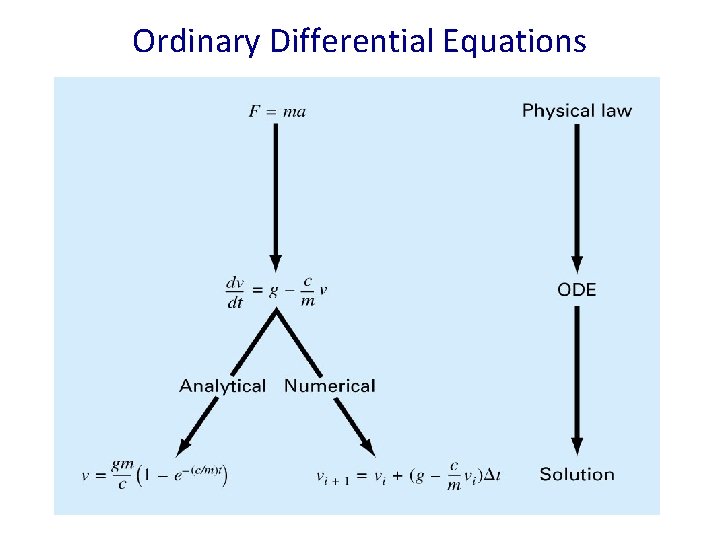
Ordinary Differential Equations Part 7 • Equations which are composed of an unknown function and its derivatives are called differential equations. v - dependent variable t - independent variable • Differential equations play a fundamental role in engineering because many physical phenomena are best formulated mathematically in terms of their rate of change.

Ordinary Differential Equations • When a function involves one dependent variable, the equation is called an ordinary differential equation (ODE). • A partial differential equation (PDE) involves two or more independent variables.

Ordinary Differential Equations Differential equations are also classified as to their order: 1. A first order equation includes a first derivative as its highest derivative. - Linear 1 st order ODE - Non-Linear 1 st order ODE

Ordinary Differential Equations 2. A second order equation includes a second derivative. - Linear 2 nd order ODE - Non-Linear 2 nd order ODE • Higher order equations can be reduced to a system of first order equations, by redefining a variable.

Ordinary Differential Equations

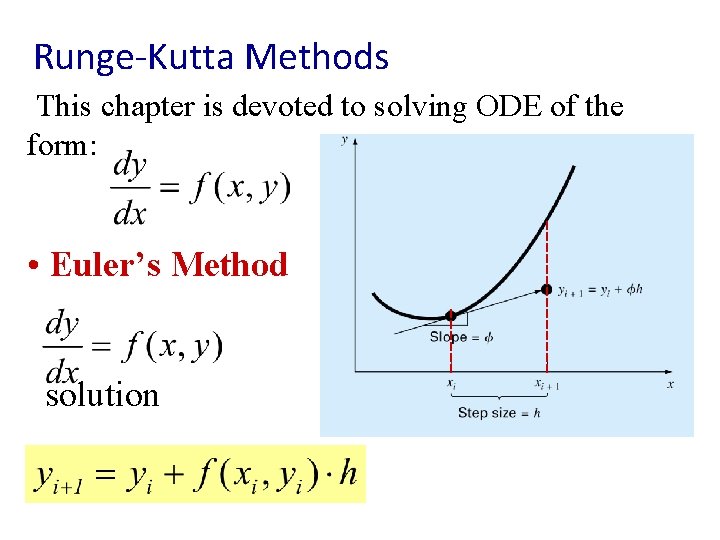
Runge-Kutta Methods This chapter is devoted to solving ODE of the form: • Euler’s Method solution

Runge-Kutta Methods

Euler’s Method: Example Obtain a solution between x = 0 to x = 4 with a step size of 0. 5 for: Initial conditions are: x = 0 to y = 1 Solution:

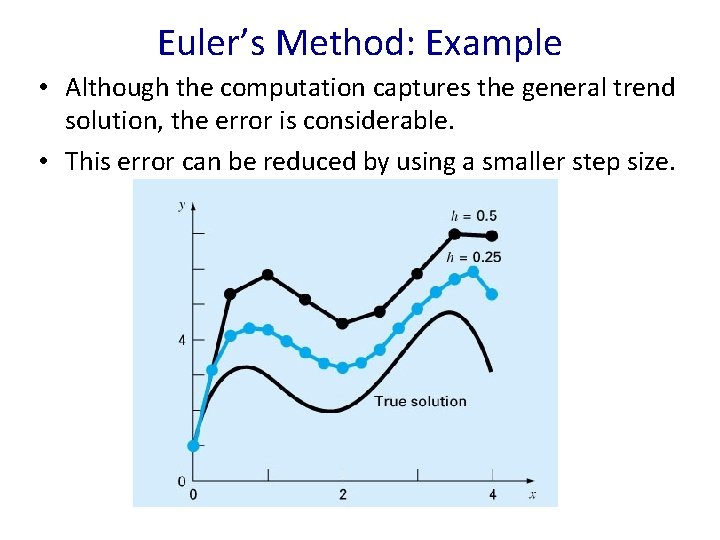
Euler’s Method: Example • Although the computation captures the general trend solution, the error is considerable. • This error can be reduced by using a smaller step size.

System of Ordinary Differential Equations The solution is finding y 1, y 2, y 3, …yn

Euler’s Method: Example Obtain a solution between x= 0 & 4 (step size of 0. 5) Initial conditions are: x = 0 ; y 1= 4 & y 2 = 6 Solution: X 0 0. 5 1 1. 5 2 y 1 4 3 2. 25 1. 687 1. 265628 y 2 6 6. 9 7. 715 8. 44525 9. 094087

Improvements of Euler’s method • A fundamental source of error in Euler’s method is that the derivative at the beginning of the interval is assumed to apply across the entire interval. • Simple modifications are available: – Heun’s Method – The Midpoint Method – Ralston’s Method

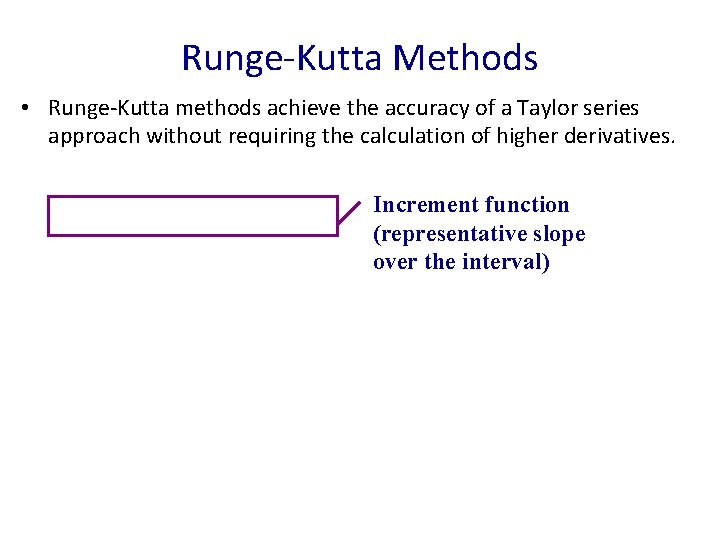
Runge-Kutta Methods • Runge-Kutta methods achieve the accuracy of a Taylor series approach without requiring the calculation of higher derivatives. Increment function (representative slope over the interval)

Runge-Kutta Methods Various types of RK methods can be devised by employing different number of terms in the increment function as specified by n. 1. First order RK method with n=1 is Euler’s method. • 2. Second order RK methods: • Values of a 1, a 2, p 1, and q 11 are evaluated by setting the second order equation to Taylor series expansion to the second order term.

Runge-Kutta Methods • Three equations to evaluate the four unknowns constants are derived: A value is assumed for one of the unknowns to solve for the other three.

Runge-Kutta Methods • We can choose an infinite number of values for a 2, there an infinite number of second-order RK methods. • Every version would yield exactly the same results if the solution to ODE were quadratic, linear, or a constant. • However, they yield different results if the solution is more complicated (typically the case).

Runge-Kutta Methods Three of the most commonly used methods are: • Huen Method with a Single Corrector (a 2=1/2) • The Midpoint Method (a 2= 1) • Raltson’s Method (a 2= 2/3)

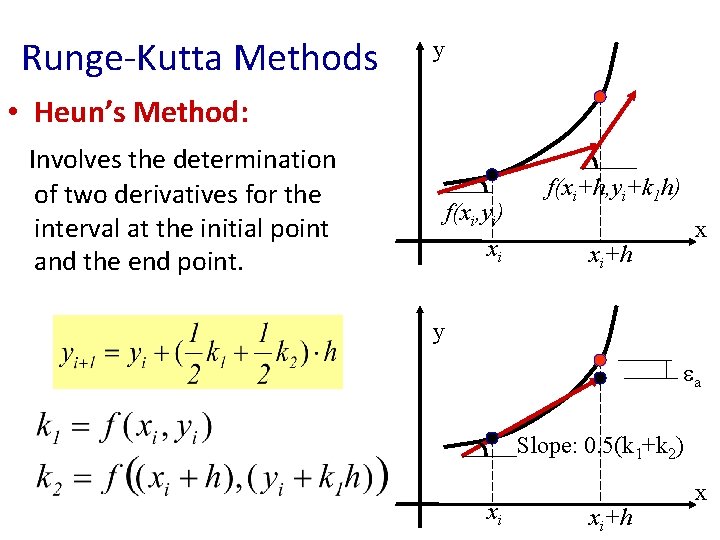
Runge-Kutta Methods y • Heun’s Method: Involves the determination of two derivatives for the interval at the initial point and the end point. f(xi, yi) xi f(xi+h, yi+k 1 h) x xi+h y ea Slope: 0. 5(k 1+k 2) xi xi+h x

Heun’s Method - Example Obtain a solution between x=0 & 4 (step size = 0. 5) for: Initial conditions are: x = 0 to y = 1, use Heun’s method Chapter 25

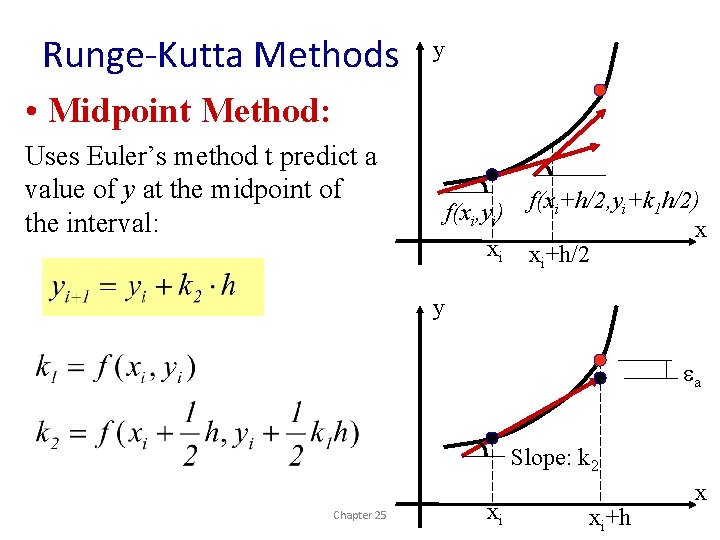
Runge-Kutta Methods y • Midpoint Method: Uses Euler’s method t predict a value of y at the midpoint of the interval: f(xi, yi) xi f(xi+h/2, yi+k 1 h/2) x xi+h/2 y ea Slope: k 2 Chapter 25 xi xi+h x

Midpoint Method (Example 25. 6, P 705) Obtain a solution between x=0 & 4 (step size = 0. 5) for: Initial conditions are: x = 0 to y = 1, use Midpoint method Chapter 25

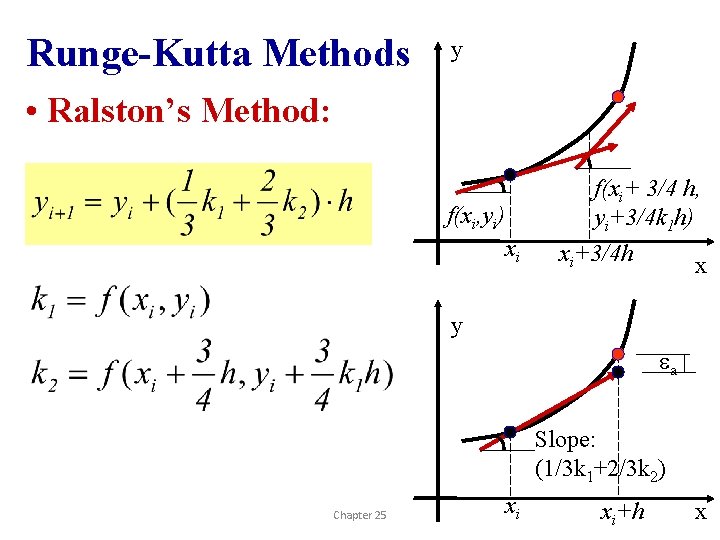
Runge-Kutta Methods y • Ralston’s Method: f(xi, yi) xi f(xi+ 3/4 h, yi+3/4 k 1 h) xi+3/4 h x y ea Slope: (1/3 k 1+2/3 k 2) Chapter 25 xi xi+h x

Chapter 25 24

Runge-Kutta Methods 3. Third order RK methods Chapter 25

Runge-Kutta Methods 4. Fourth order RK methods Chapter 25

Comparison of Runge-Kutta Methods Use first to fourth order RK methods to solve the equation from x = 0 to x = 4 Initial condition y(0) = 2, exact answer of y(4) = 75. 33896 Chapter 25

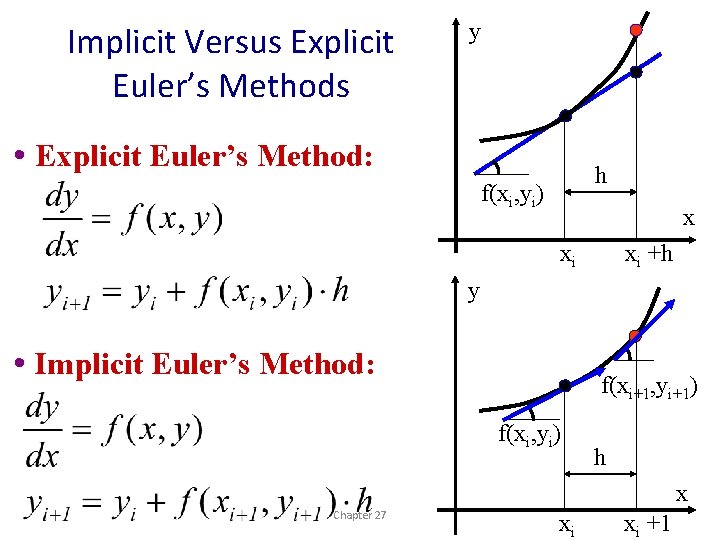
Implicit Versus Explicit Euler’s Methods y • Explicit Euler’s Method: h f(xi, yi) x xi xi +h y • Implicit Euler’s Method: f(xi+1, yi+1) f(xi, yi) h x Chapter 27 xi xi +1

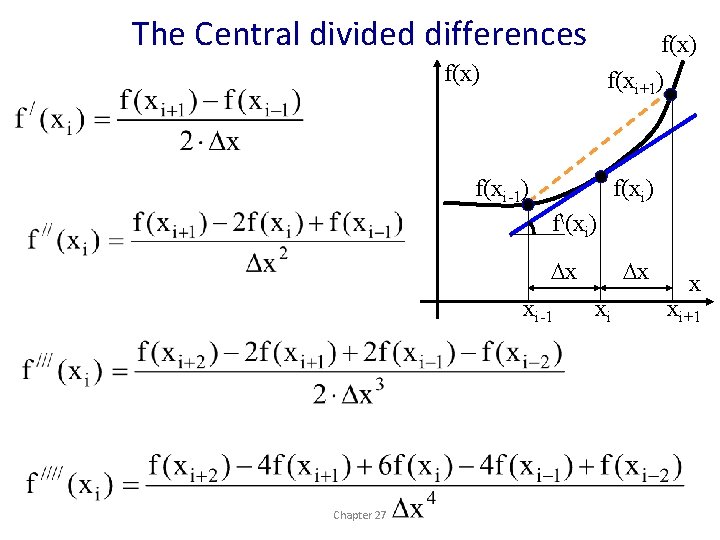
The Finite Difference Method • The previous central divided differences are substituted for the derivatives in the original equation. • Thus a differential equation is transformed into a set of simultaneous algebraic equations that can be solved by the methods described earlier. Chapter 27

The Central divided differences f(x) f(xi+1) f(xi-1) f(xi) f(xi) Dx xi-1 Chapter 27 Dx xi+1

The Finite Difference Method-Example Solve the following 2 nd order ODE for initial conditions of T(0) = T 1 and T(L) = T 2 Where Ta and h/ are constants. Solution: • Using the divided differences equations: • Substitute into the original DE for d 2 T/dx 2: Chapter 27

The Finite Difference Method-Example • Now collecting terms gives: • The above equation is now applied at each of the interior point. • The first point and the last point are specified by the boundary conditions. • So if there is 5 points (including the first and the last point) we will have 3 equations in 3 unknowns. Chapter 27

The Finite Difference Method: Example Solve the following 2 nd order ODE for initial conditions of y(0) = 5 and y(10) = -1. 5, Use Dx = 2 • Using the divided differences equations: Chapter 27

The Finite Difference Method: Example • Substitute into the original DE for d 2 y/dx 2 and dy/dx: • Now collecting terms gives and substitute for Dx =2: • The above equations will be used to find the y’s at 2, 4, 6 and 8 where y(0) = 5 and y(10) = -1. 5 Chapter 27

The Finite Difference Method: Example Chapter 27

The Finite Difference Method: Example • Or in a matrix format: • Now you can use for example Gauss elimination to solve these equations. Chapter 27

PART 8 Partial Differential Equations PDEs Finite Difference Method Finite Element Method Chapter 29

Partial Differential Equations Chapter 29

Partial Differential Equations • A partial differential equation (PDE) involves two or more independent variables. For example: 1. Laplace equation 2. Diffusion equation 3. Wave equation Chapter 29

Partial Differential Equations 1. Finite Difference Method • Similar to the ODE, central divided differences are substituted for the partial derivatives in the original equation. • Thus a partial differential equation is transformed into a set of simultaneous algebraic equations that can be solved by the methods described earlier. Chapter 29

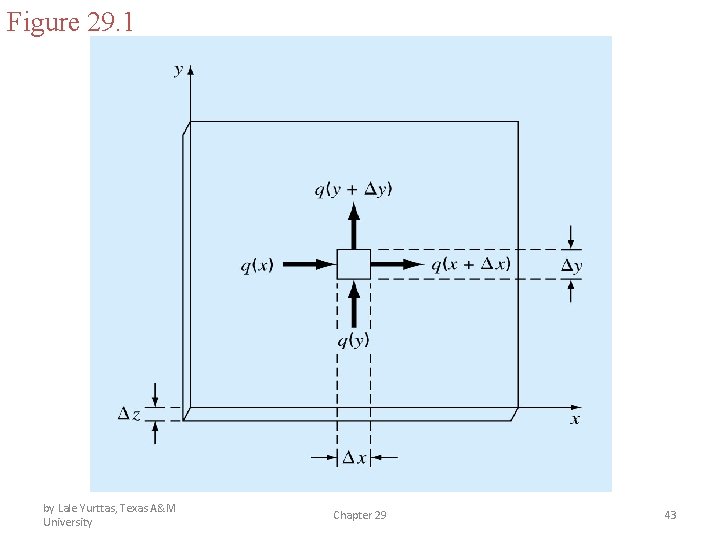
Partial Differential Equations The Central divided differences y i, j+1 i-1, j i+1, j i, j-1 Chapter 29 x

Finite Difference: Elliptic Equations • Because of its simplicity and general relevance to most areas of engineering, we will use a heated plate as an example for solving elliptic PDEs. Chapter 29 42

Figure 29. 1 by Lale Yurttas, Texas A&M University Chapter 29 43

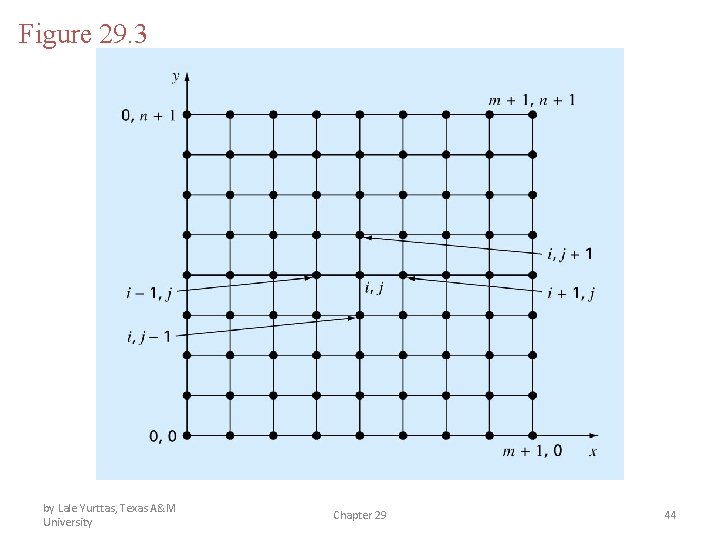
Figure 29. 3 by Lale Yurttas, Texas A&M University Chapter 29 44

The Laplacian Difference Equations/ Laplace Equation O[D(x)2] O[D(y)2] Laplacian difference equation. Holds for all interior points Chapter 29

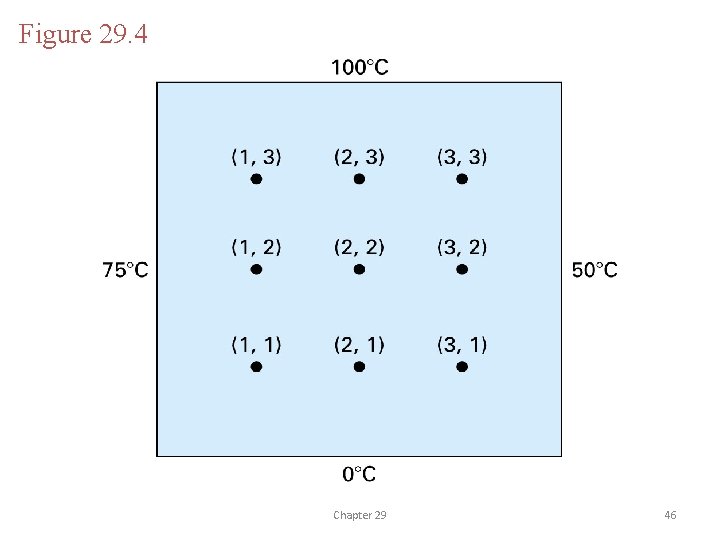
Figure 29. 4 Chapter 29 46

• In addition, boundary conditions along the edges must be specified to obtain a unique solution. • The simplest case is where the temperature at the boundary is set at a fixed value, Dirichlet boundary condition. • A balance for node (1, 1) is: • Similar equations can be developed for other interior points to result a set of simultaneous equations. Chapter 29 47

• The result is a set of nine simultaneous equations with nine unknowns: Chapter 29 48

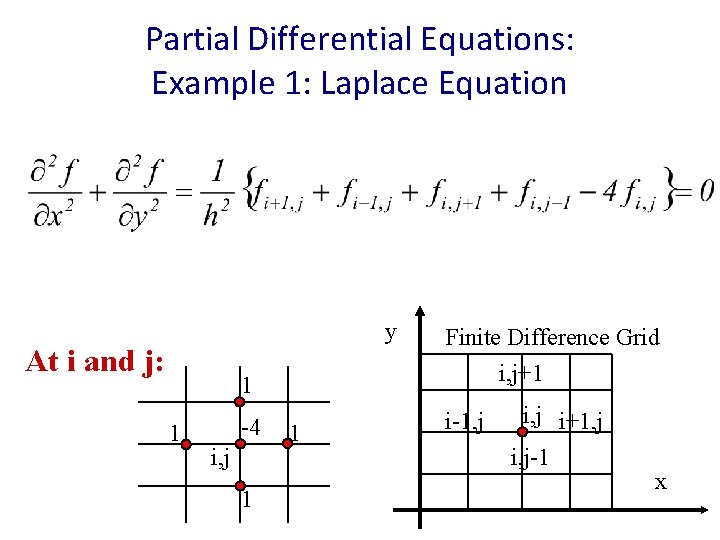
Partial Differential Equations: Example 1: Laplace Equation Laplace: Substitute with the Central divided differences and assuming that Dx = Dy = h

Partial Differential Equations: Example 1: Laplace Equation y At i and j: 1 1 Finite Difference Grid i, j+1 -4 i-1, j i, j 1 1 i, j i+1, j i, j-1 x

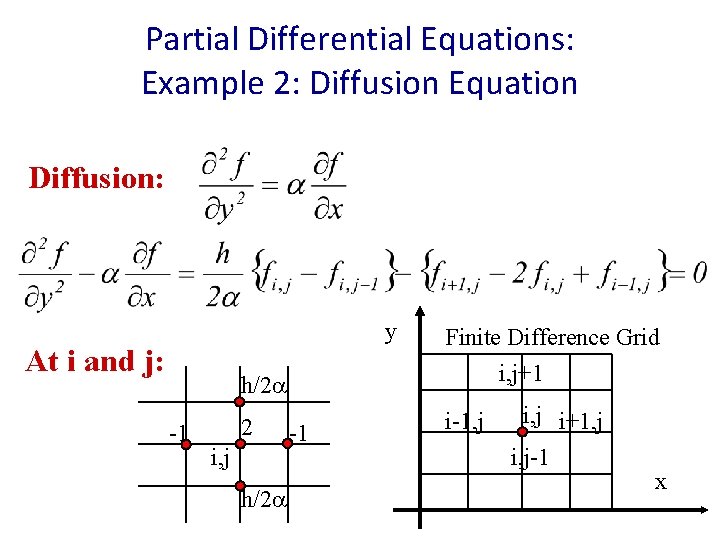
Partial Differential Equations: Example 2: Diffusion Equation Diffusion: Substitute with the Central divided differences and assuming that Dx = Dy = h:

Partial Differential Equations: Example 2: Diffusion Equation Diffusion: y At i and j: -1 h/2 a Finite Difference Grid i, j+1 2 i-1, j i, j h/2 a -1 i, j i+1, j i, j-1 x