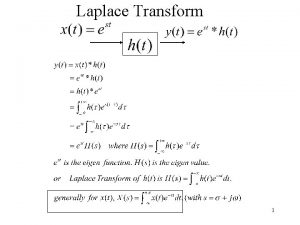Physics for informatics Lecture 3 Laplace transform Ing

Physics for informatics Lecture 3 Laplace transform Ing. Jaroslav Jíra, CSc.

The Laplace transform What is it good for? • Solving of differential equations • System modeling • System response analysis • Process control application

The Laplace transform Solving of differential equations procedure A system analysis can be done by several simple steps 1. Finding differential equations describing the system 2. Obtaining the Laplace transform of these equations 3. Performing simple algebra to solve for output or variable of interest 4. Applying inverse transform to find solution

The Laplace transform The definition 1. The Laplace transform is an operator that switches a function of real variable f(t) to the function of complex variable F(s). 2. We are transforming a function of time - real argument t to a function of complex angular frequency s. 3. The Laplace transform creates an image F(s) of the original function f(t) where s= σ+ iω

The Laplace transform Restrictions 1. The function f(t) must be at least piecewise continuous for t ≥ 0. 2. |f(t)| ≤ Meαt where M and α are constants. The function f(t) must be bounded, otherwise the Laplace integral will not converge. 3. We assume that the function f(t) = 0 for all t < 0

The Laplace transform Inverse Laplace transform 1. Inverse transform requires complex analysis to solve 2. If there exists a unique function F(s)=L[f(t)], then there is also a unique function f(t)=L-1[F(s)] 3. Using the previous statement, we can simply create a set of transform pairs and calculate the inverse transform by comparing our image with known results in time scope

The Laplace transform Basic properties Linearity Scaling in time Time shift Frequency shift

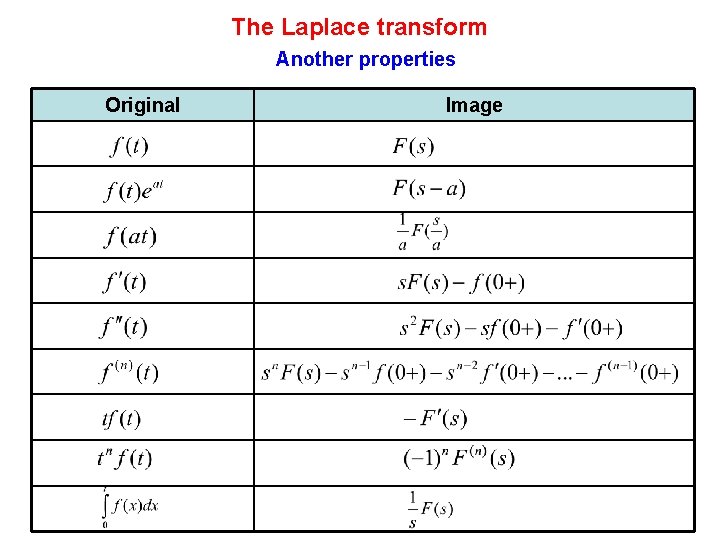
The Laplace transform Another properties Original Image

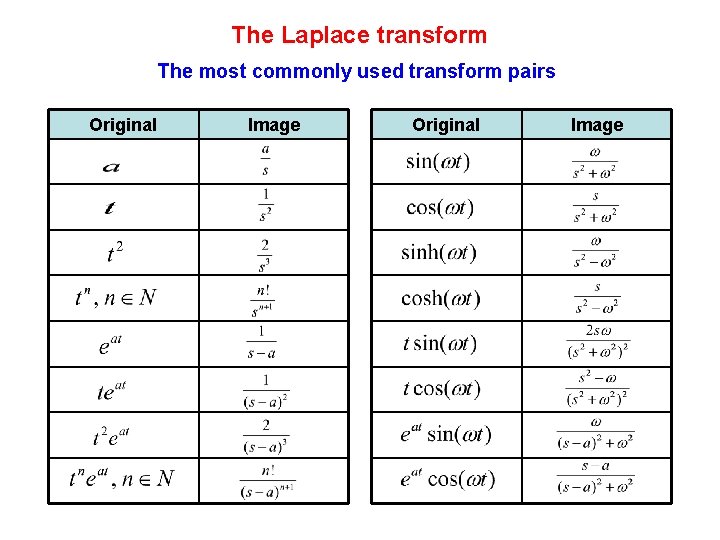
The Laplace transform The most commonly used transform pairs Original Image

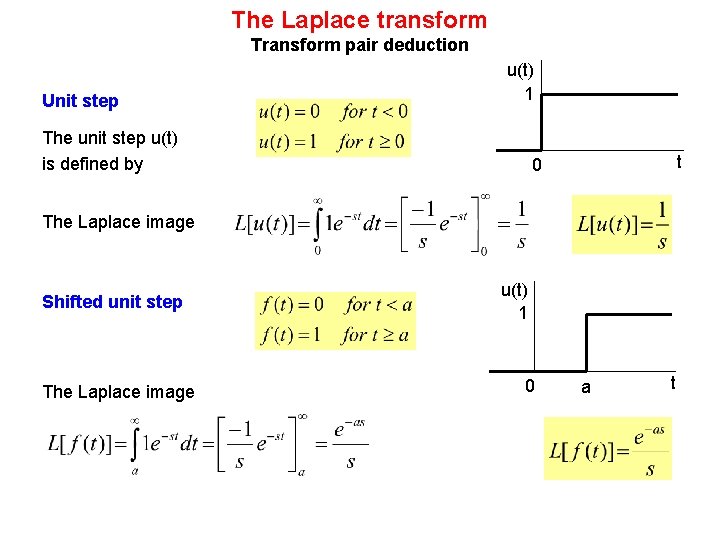
The Laplace transform Transform pair deduction Unit step u(t) 1 The unit step u(t) is defined by t 0 The Laplace image Shifted unit step The Laplace image u(t) 1 0 a t

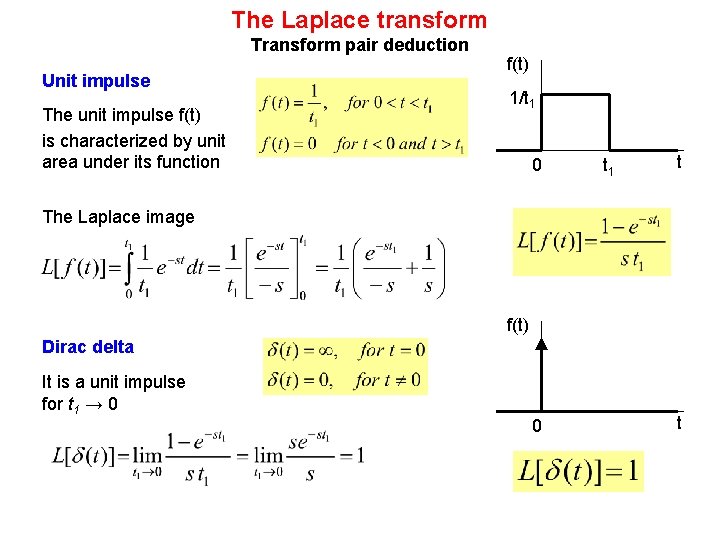
The Laplace transform Transform pair deduction Unit impulse The unit impulse f(t) is characterized by unit area under its function f(t) 1/t 1 0 t 1 t The Laplace image f(t) Dirac delta It is a unit impulse for t 1 → 0 0 t

The Laplace transform Transform pair deduction Exponential function Linear function Per partes integration

The Laplace transform Transform pair deduction Square function The n-th power function Per partes integration

The Laplace transform Transform pair deduction Cosine function Sine function

The Laplace transform Transform pair deduction Time shift f(t) f(t-a) The original function f(t) is shifted in time to f(t-a) 0 Frequency shift a t

The Laplace transform Property deduction Time differentiation Per partes integration

The Laplace transform Property deduction Time integration Per partes integration

Inverse Laplace transform The algorithm of inverse Laplace transform Since the F(s) is mostly fractional function, then the most important step is to perform partial fraction decomposition of it. Depending on roots in denominator, we are looking for the following functions, where A and B are real numbers: for a single real root s= a for a double real root s= a for a triple real root s= a for a pair of pure imaginary roots s= ± iω for a pair of complex conjugated roots s= a ± iω

Inverse Laplace transform Basic examples of partial fraction decomposition to find the original f(t) Two distinct real roots The equation s 2 + 4 s + 3= 0 has two distinct real roots s 1= -3 and s 2= -1 We have to find coefficients A and B for Multiplying the equation by its denominator Now we can substitute Decomposed F(s) so the original function

Inverse Laplace transform One real root and one real double root The denominator has a single root s 1= -1 and a double root s 23= -3 We are looking for coefficients A, B and C Multiplying the equation by its denominator Now we can substitute to get A, B; the C coefficient can be obtained by comparison of s 2 factors Decomposed F(s) so the original function

Inverse Laplace transform Two pure imaginary roots Since we know, that it will be helpful to rearrange the original formula Now we can directly write the result

Inverse Laplace transform One real root and two pure imaginary roots We are looking for coefficients A, B and C Multiplying the equation by its denominator Now we can substitute to get A; B, C coefficients can be obtained by comparison of s 0, s 2 factors Decomposed F(s) so the original function

Inverse Laplace transform Two complex conjugated roots We have to rearrange the denominator in the first step Decomposed F(s) Now we have to assemble all necessary relations so the original function

Solving of differential equations by the Laplace transform Example 1 Find the x(t) on the interval <0, ∞) The image of desired function is From the former definitions we know, that Then we can write The original function

Solving of differential equations by the Laplace transform Example 2 Function on the right side Necessary relations Equation in the Laplace form

Solving of differential equations by the Laplace transform Example 2 - continued A formula for the X(s) after the partial fraction decomposition after some small arrangements The original function

Solving of differential equations by the Laplace transform Example 3 Homogeneous second order LDR Necessary relations Equation in the Laplace form The original function

Solving of differential equations by the Laplace transform Example 4 Inhomogeneous second order LDR Necessary relations Equation in the Laplace form knowing that The original function

Solving of differential equations by the Laplace transform Example 5 Integro-differential equation Necessary relations Equation in the Laplace form The original function