Ordinary differential equations ODE An nth order ordinary

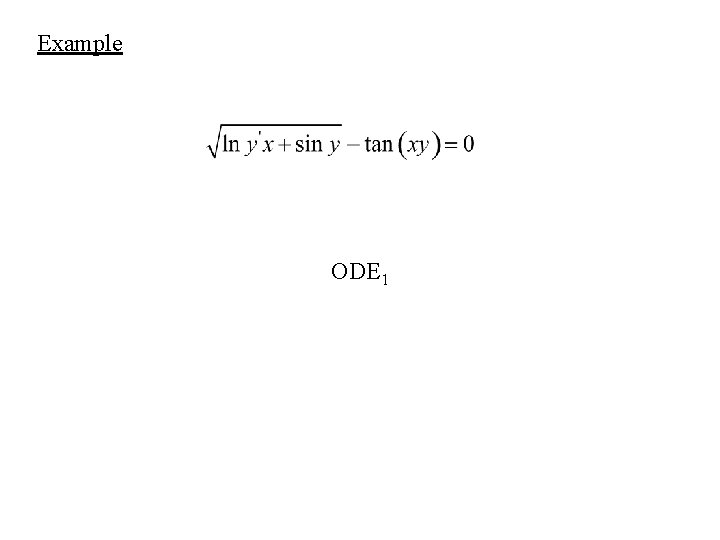
















- Slides: 21

Ordinary differential equations - ODE An n-th order ordinary differential equation (ODEn) is an equation where is a known function in n + 1 variables and y = y (x) is an unknown function with derivatives
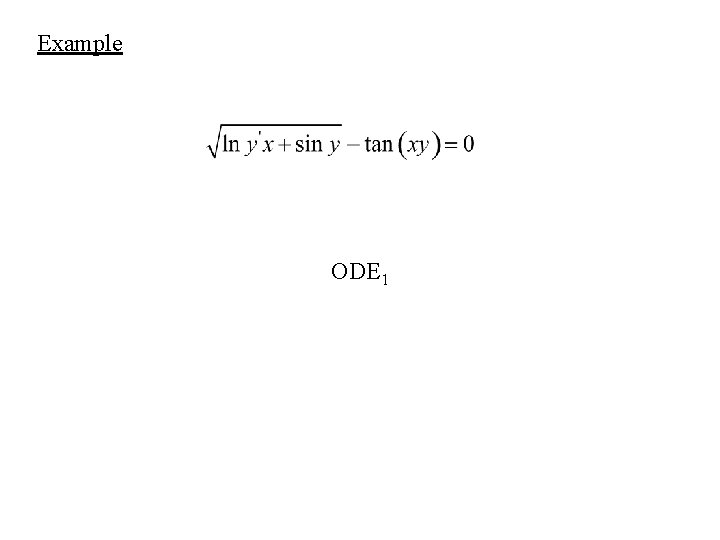
Example ODE 1

Example ODE 1

Example ODE 1

Example ODE 4

Example ODE 3

Example ODE 5

Solution to a differential solution Defining a solution to a general differential equation of order n in an exact way is rather a tricky business. However, since in most of the ordinary situations, this notion is quite intuitive, by way of an example, we will only define precisely what we understand under a solution to a first order differential solution.

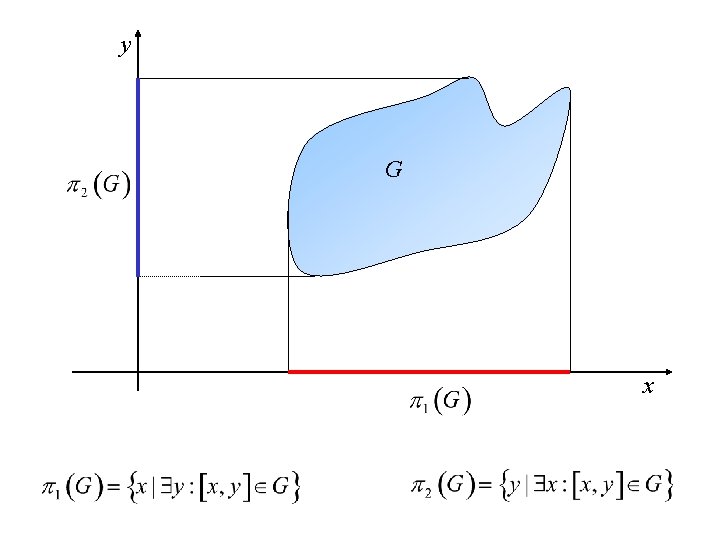
y G x

Let be a differential equation where continuous function on We say that a function is a solution to if u (x) has a continuous derivative in some interval the entire graph of u (x) lies in G, that is, when substituting u for y in and the equation holds for every in

Using another example, we shall now explain the difference between a general , particular, and singular solution to a differential equation:

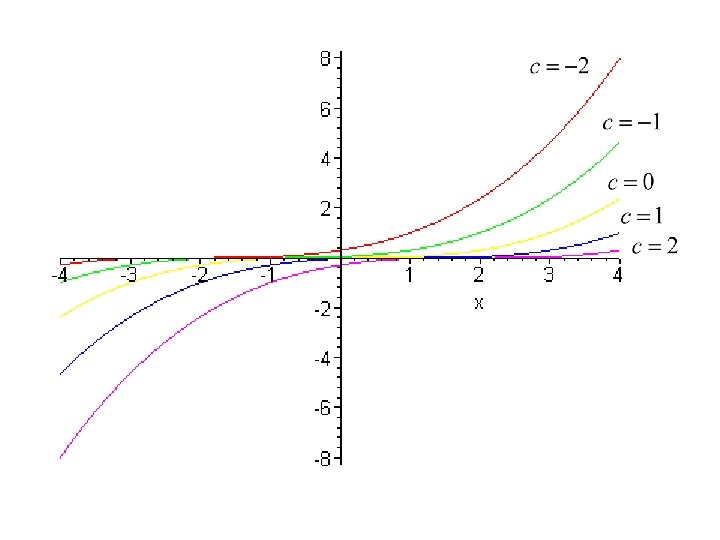
Let us have a differential equation Since no other restrictions are given, G is E 2 and we can easily verify that for any is a solution to and so is the function


is a general solution to a general solution represents a set of solutions to a differential equation that only differ from each other by the values of a parameter (in a general case of several parameters) lying in a set of admissible values

is a particular solution to a particular solution is a solution to a differential equation that can be obtained from a general solution by choosing a value of the parameter (parameters)

is a singular solution to a differential equation is such a solution for which no value of the parameter in a general solution exists, that is, it cannot be obtained by substituting into a general solution.

To start off we will concern ourselves with first order ordinary differential equations or ODE 1 sometimes just ODE.

Cauchy initial problem We are to find a solution to the differential equation such that it satisfies an initial condition

A solution to a Cauchy initial problem in the general case may not be easy to find. Sometimes it can even be proved that no "analytic" solution exists. A solution is called analytic if it can be expressed in terms of a finite set of "basic known functions" combining them using a finite number of arithmetic operations and embeddings.

All these people may ask the following questions: given a Cauchy initial problem is there a solution to it? under what circumstances does a Cauchy problem with a given initial condition have a unique solution?

We will try to find answers to these questions later on. Now we will concentrate on the more practical side to this problem, that is, how we can in favourable, particular cases find a solution to a Cauchy problem.
 Midpoint method formula
Midpoint method formula Non linear ode
Non linear ode General solutions to differential equations
General solutions to differential equations Order and degree of differential equation ppt
Order and degree of differential equation ppt Ordinary differential equations example
Ordinary differential equations example Ordinary differential equations example
Ordinary differential equations example Piecewise differential equation
Piecewise differential equation Methods of characteristics
Methods of characteristics What is a first order equation
What is a first order equation First ode
First ode Second order differential equation
Second order differential equation What is a first order equation
What is a first order equation Separable partial differential equations
Separable partial differential equations First-order differential equations
First-order differential equations Higher order linear differential equations
Higher order linear differential equations Roots of equation
Roots of equation Find the indicated real n th root(s) of a
Find the indicated real n th root(s) of a Ordinary point definition
Ordinary point definition Via optica
Via optica Differential equations projects
Differential equations projects Classification of pde
Classification of pde Cengage differential equations
Cengage differential equations