Rwnania rniczkowe zwyczajne ang ordinary differential equations ODE

Równania różniczkowe zwyczajne (ang. ordinary differential equations, ODE) Równaniem różniczkowym zwyczajnym rzędu pierwszego nazywamy równanie postaci gdzie jest daną funkcją. Rozwiązaniem takiego równania nazywamy każdą funkcję która jest różniczkowalna i spełniania równość Często rozwiązanie oznaczać także symbolem y(t), więc powyższy warunek zapiszemy jako

Przykład Rozważmy równanie Przykładowe rozwiązanie Sprawdzamy przez podstawienie Podane rozwiązanie jest jedyne, gdyż na przykład funkcja też spełnia to równanie.

Przykład Rozważmy równanie Sprawdzamy, że funkcja jest rozwiązaniem: W ogólnym przypadku każda funkcja postaci jest rozwiązaniem tego równania.

Zagadnieniem początkowym (zagadnieniem początkowym) nazywamy następujące dwa warunki gdzie Cauchy’ego, problemem są danymi liczbami (warunek początkowy), a jest daną funkcją. Rozwiązaniem tak postawionego problemu jest dowolna funkcja y=y(t), która spełnia równanie, czyli y’(t)=f(t, y(t)) dla t z otoczenia t 0, a ponadto spełnia warunek początkowy, czyli y(t 0)= y 0.

Przykład Jakie jest rozwiązanie zagadnienia Cauchy’ego Rozwiązanie ogólne równania y’ = t y ma postać Podstawiamy warunek początkowy y(0)=2, co daje C=2. Zatem rozwiązaniem zagadnienia Cauchy’ego jest funkcja

Przykład Jakie jest rozwiązanie poniższego zagadnienia Cauchy’ego Rozwiązaniem problemu jest funkcja stale równa zero Ale rozwiązaniem jest także funkcja Mamy zatem przykład niejednoznaczności rozwiązania! Okazuje się jednak, że przy dość ogólnych założeniach rozwiązanie zagadnienia Cauchy’ego jest jednak jednoznaczne. Taka sytuacja najczęściej występuje w zastosowaniach równań różniczkowych zwyczajnych.

Synteza bromowodoru z pierwiastków jest reakcją złożoną o sumarycznym równaniu W roku 1906 wyznaczono eksperymetalnie następujące równanie kinetyczne tej reakcji Czasami równanie to jest zapisywane równoważnie tak Stałe kinetyczne k 1 oraz k 2 zależą od warunków przebiegu reakcji (temperatura, ciśnienie itp. ). Eksperymetalnie wyznaczono, że w zwykłych warunkach k 2≈0, 1.

Synteza bromowodoru z pierwiastków (c. d. ) Wprowadzamy oznaczenie y(t) = [HBr] oraz uwzględniamy bilans masy w równaniu co daje dodatkowe zależności Po podstawieniu do równania kinetycznego na d[HBr]/dt otrzymamy

Synteza bromowodoru z pierwiastków (c. d. ) Przeprowadzając symulację podanego układu dynamicznego możemy precyzyjnie przewidzieć ewolucję stężenia składników – a w szczególności przewidzieć czas trwania reakcji. Prawdziwa kinetyka syntezy bromowodoru. Gdyby kinetyka syntezy bromowodoru była analogiczna do syntezy chlorowodoru.

Układy równań różniczkowych zwyczajnych (ODEs) W ogólnym przypadku możemy mieć n niewiadomych funkcji y 1(t), …, yn(t) oraz n równań: z warunkami początkowymi: gdzie liczby są dane.

Równania Lotki — jedna reakcja autokatalityczna Rozważmy następującą sekwencję reakcji elementarnych: Powyższy mechanizm opisuje ostatecznie sumaryczną reakcję A B. Z postaci tego mechanizmu możemy postulować następujący układ równań różniczkowych zwyczajnych:

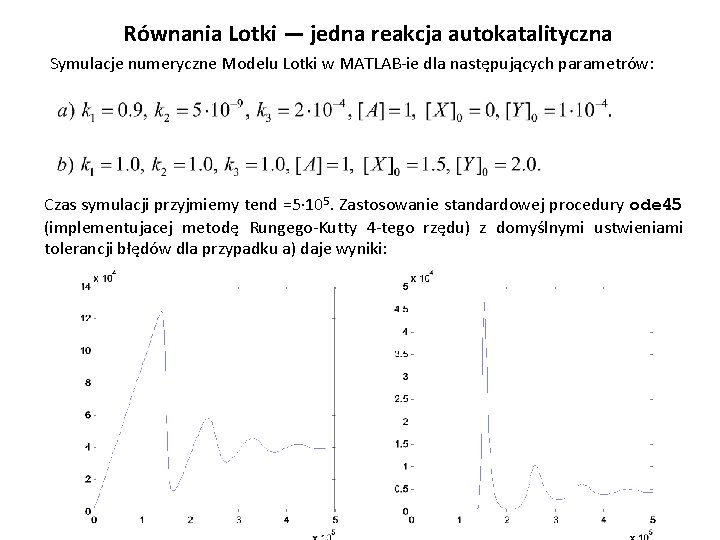
Równania Lotki — jedna reakcja autokatalityczna Symulacje numeryczne Modelu Lotki w MATLAB-ie dla następujących parametrów: Czas symulacji przyjmiemy tend =5· 105. Zastosowanie standardowej procedury ode 45 (implementujacej metodę Rungego-Kutty 4 -tego rzędu) z domyślnymi ustwieniami tolerancji błędów dla przypadku a) daje wyniki:

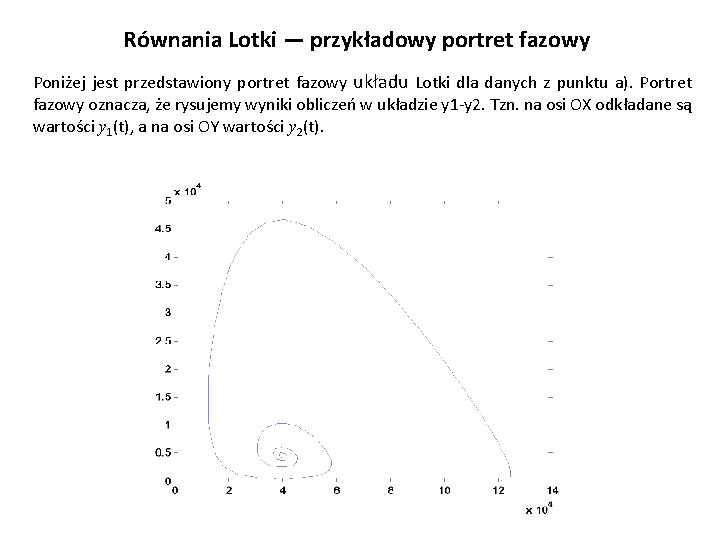
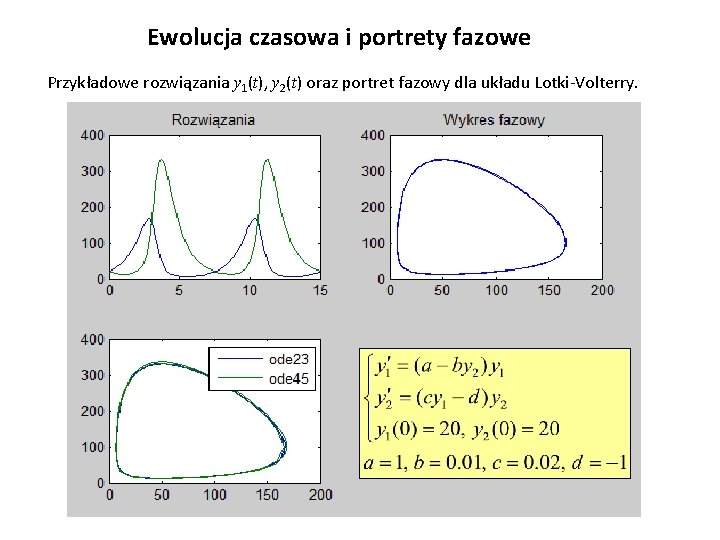
Równania Lotki — przykładowy portret fazowy Poniżej jest przedstawiony portret fazowy układu Lotki dla danych z punktu a). Portret fazowy oznacza, że rysujemy wyniki obliczeń w układzie y 1 -y 2. Tzn. na osi OX odkładane są wartości y 1(t), a na osi OY wartości y 2(t).

Równania Lotki-Volterry (dwie reakcje autokatalityczne) Jest to model podobny do modelu Lotki, ale tym razem występują dwie reakcje autokatalityczne: Powyższa sekwencja opisuje sumaryczną reakcję A B. Z postaci podanego mechanizmu możemy postulować następujący układ równań różniczkowych zwyczajnych:

Równania Lotki-Volterry (dwie reakcje autokatalityczne – c. d. ) W układzie reakcji Lotki-Volterry zakładamy, że stężenie reagenta A jest stałe: [A]=const. Wprowadzając wygodne oznaczenia: [X]=y 1(t), [Y]=y 2(t), [A]=a, możemy układ równań zapisać następująco: Układ ten ma ciekawą własność – występują w nim rozwiązania okresowe. Dokładnej, dla każdej pary warunków początkowych y 1(0)=y 10 > 0, y 2(0)=y 20 > 0 rozwiązania y 1(t), y 2(t) istnieją dla wszystkich t 0 i są funkcjami okresowymi.

Układ Lotki-Volterry jako prosty model drapieżnik-ofiara Ten sam układ równań może być wykorzystany do opisu prostego modelu interakcji pomiędzy dwoma populacjami: ofiar i drapieżników. gdzie

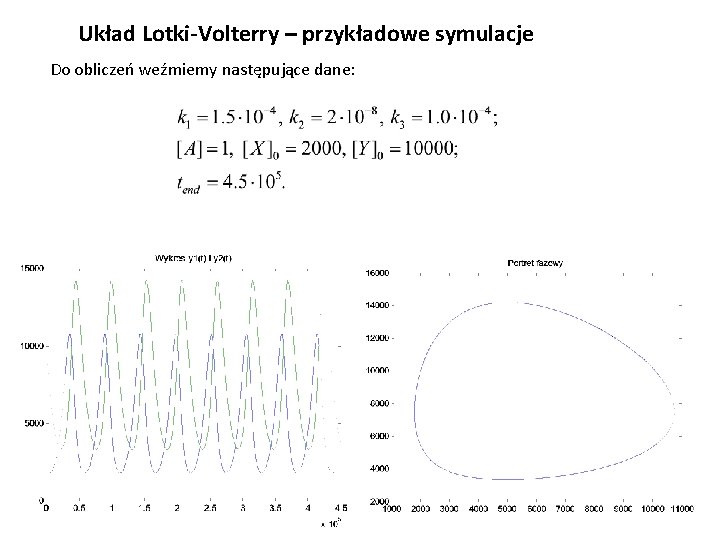
Układ Lotki-Volterry – przykładowe symulacje Do obliczeń weźmiemy następujące dane:

Ewolucja czasowa i portrety fazowe Przykładowe rozwiązania y 1(t), y 2(t) oraz portret fazowy dla układu Lotki-Volterry.

Bruselator Jest to teoretyczny model dla autokatalitycznej reakcji z wszystkimi etapami nieodwracalnymi i takimi samymi stałymi szybkości k 1=k 2=k 3=k 4=1. Procesem sumarycznym jest: A+B D+E. Powyższy mechanizm prowadzi do następującego układu, gdy szybkość reakcji jest określona przez postacie reakcji

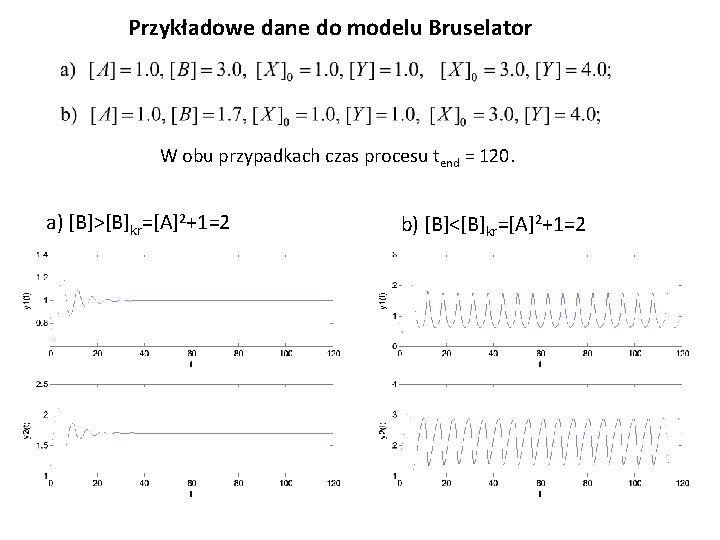
Wprowadzamy wygodniejsze oznaczenia: Parametry a i b są dodatnimi stałymi. Niewiadomymi są funkcje y 1=y 1(t), y 2=y 2(t). Równania opisujące Bruselator mają teraz postać: Powyższy układ równań generuje rozwiązania, których jakościowy charakter może istotnie się różnić w zależności od wzajemnej relacji parametrów a i b. W szczególności punkt stacjonarny tego układu staje się niestabilny gdy

Przykładowe dane do modelu Bruselator W obu przypadkach czas procesu tend = 80. Jeśli zmieniając stężenie [B] osiągniemy wartość krtytyczną [B]kr=[A]2+1, to następuje tzw. bifurkacja Hopfa. Dotychczasowy pojedynczy stan stacjonarny traci stabilność – w zakresie stężeń [B] > [A]2 + 1 obserwujemy zupełnie inne zachowanie – stabilne oscylacje stężeń [X] i [Y].

Przykładowe dane do modelu Bruselator W obu przypadkach czas procesu tend = 120. a) [B]>[B]kr=[A]2+1=2 b) [B]<[B]kr=[A]2+1=2