Nonlinear Dimension Reduction Presenter Xingwei Yang The powerpoint

Nonlinear Dimension Reduction Presenter: Xingwei Yang The powerpoint is organized from: 1. Ronald R. Coifman et al. (Yale University) 2. Jieping Ye, (Arizona State University)

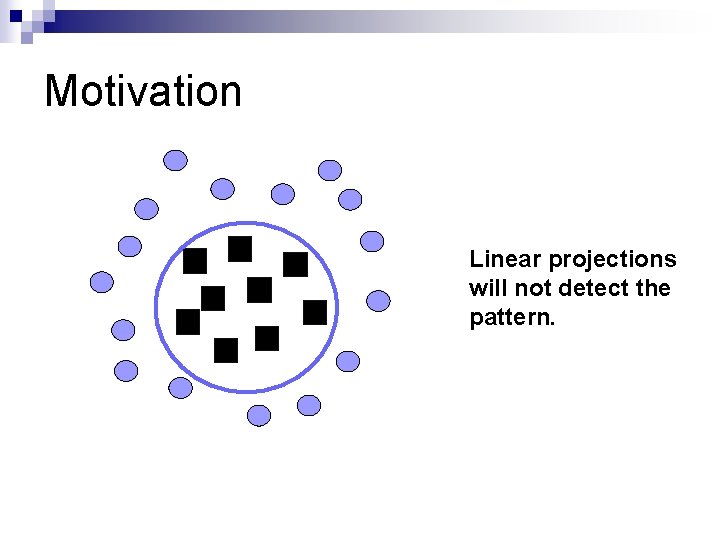
Motivation Linear projections will not detect the pattern.

Nonlinear PCA using Kernels n Traditional PCA applies linear transformation ¨ May not be effective for nonlinear data n Solution: apply nonlinear transformation to potentially very highdimensional space. n Computational efficiency: apply the kernel trick. ¨ Require PCA can be rewritten in terms of dot product. More on kernels later

Nonlinear PCA using Kernels Rewrite PCA in terms of dot product The covariance matrix S can be written as Let v be The eigenvector of S corresponding to nonzero eigenvalue Eigenvectors of S lie in the space spanned by all data points.

Nonlinear PCA using Kernels The covariance matrix can be written in matrix form: Any benefits?

Nonlinear PCA using Kernels Next consider the feature space: The (i, j)-th entry of Apply the kernel trick: K is called the kernel matrix. is

Nonlinear PCA using Kernels n Projection of a test point x onto v: Explicit mapping is not required here.

8/14 Diffusion distance and Diffusion map • A symmetric matrix Ms can be derived from M as • M and Ms has same N eigenvalues, f : left eigenvector of M y : right eigenvector of M • Under random walk representation of the graph M e : time step

Diffusion distance and Diffusion map • e has the dual representation (time step and kernel width). • If one starts random walk from location xi , the probability of landing in location y after r time steps is given by where ei is a row vector with all zeros except that ith position = 1. • For large e, all points in the graph are connected (Mi, j >0) and the eigenvalues of M

Diffusion distance and Diffusion map • One can show that regardless of starting point xi Left eigenvector of M with eigenvalue l 0=1 with • Eigenvector f 0(x) has the dual representation : 1. Stationary probability distribution on the curve, i. e. , the probability of landing at location x after taking infinite steps of random walk (independent of the start location). 2. It is the density estimate at location x.

Diffusion distance • For any finite time r, • yk and fk are the right and left eigenvectors of graph Laplacian M. • is the kth eigenvalue of M r (arranged in descending order). • Given the definition of random walk, we denote Diffusion distance as a distance measure at time t between two pmfs as with empirical choice w(y)=1/f 0(y).

Diffusion Map • Diffusion distance : • Diffusion map : Mapping between original space and first k eigenvectors as Relationship : • This relationship justifies using Euclidean distance in diffusion map space for spectral clustering. • Since , it is justified to stop at appropriate k with a negligible error of order O(lk+1/lk)t).

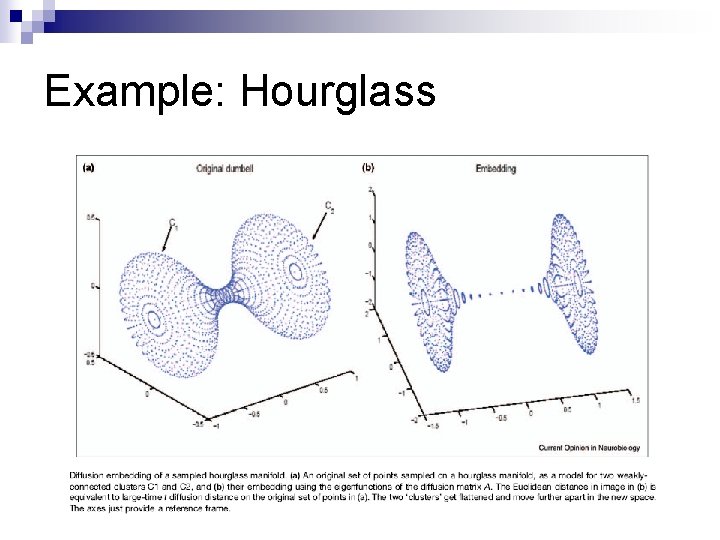
Example: Hourglass

Example: Image imbedding

Example: Lip image

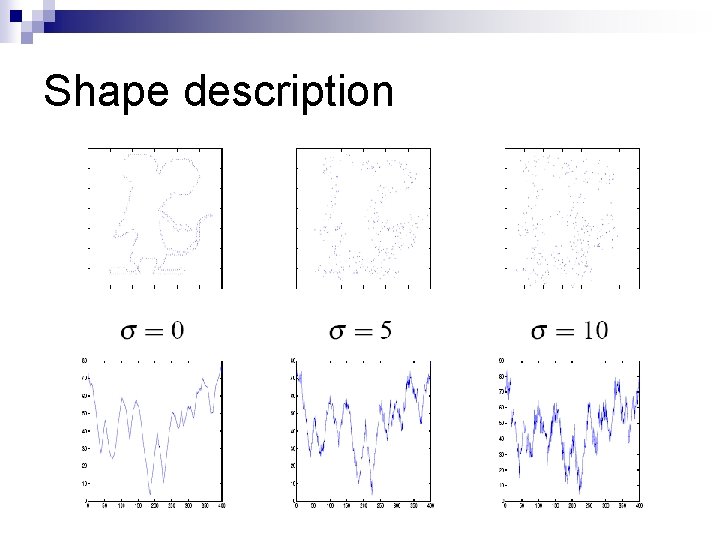
Shape description

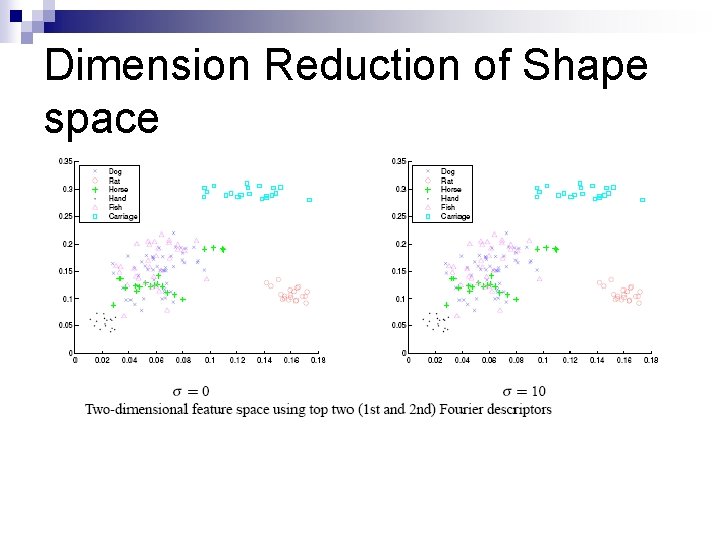
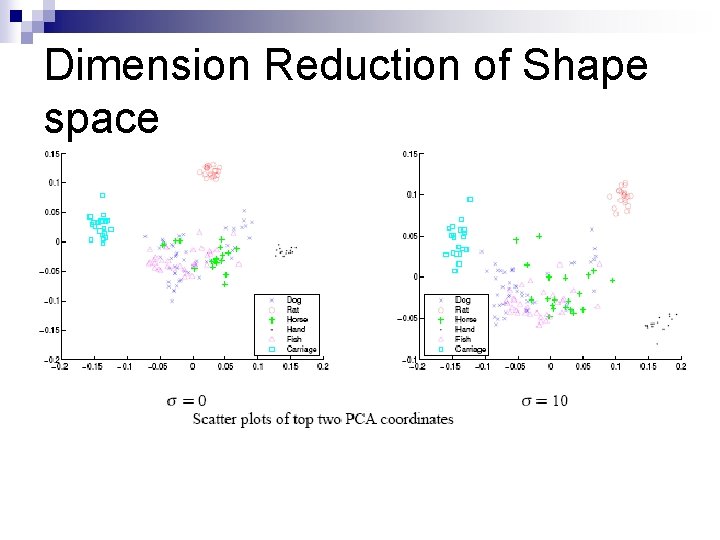
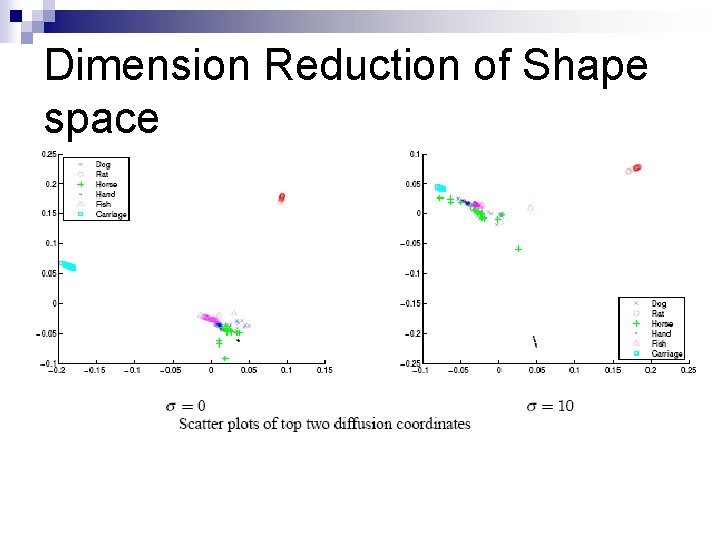
Dimension Reduction of Shape space

Dimension Reduction of Shape space

Dimension Reduction of Shape space

References Unsupervised Learning of Shape Manifolds (BMVC 2007) n Diffusion Maps(Appl. Comput. Harmon. Anal. 21 (2006)) n Geometric diffusions for the analysis of data from sensor networks (Current Opinion in Neurobiology 2005) n