Medidas de Velocidade Doppler Cap 8 Battan Velocidade

Medidas de Velocidade Doppler Cap. 8 - Battan

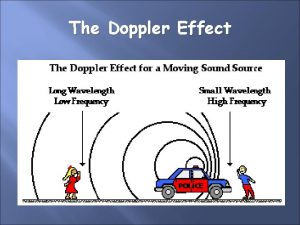
Velocidade Doppler • Além das medidas do fator refletividade do radar, alguns radares meteorológicos conseguem inferir a velocidade de propagação radial dos alvos amostrados. • Basicamente, os alvos em movimento mudam a frequência do sinal que é proporcional à sua velocidade de deslocamento. • Sendo que os radares Doppler conseguem medir as mudanças de fase nas frequências de microondas.

Efeito Doppler Assumindo que um alvo está a uma distância r do radar e que este opera em uma frequência f 0 (f=c/ ). Temos que a distância percorrida pela onda eletromagnética retroespalhada pelo alvo é d = 2 r (ida e volta). Em termos do número de onda, a distância percorrida pela onda EM é d = 2 r/ ou em radianos d = (2 r/ )2 = 4 r/
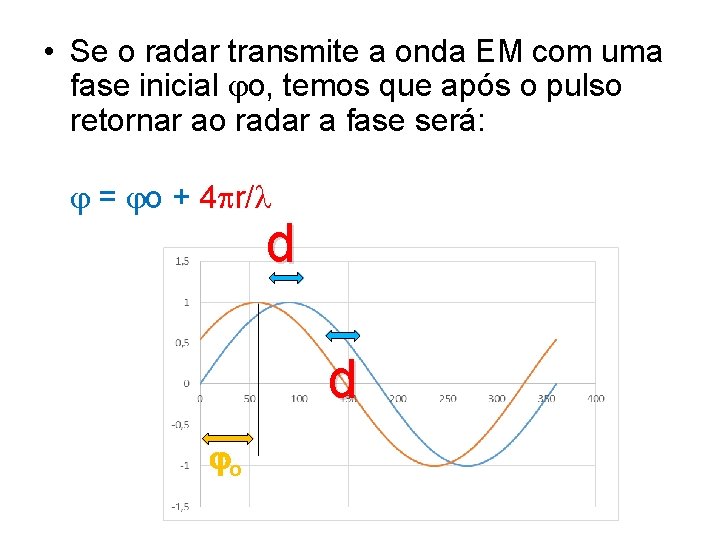
• Se o radar transmite a onda EM com uma fase inicial o, temos que após o pulso retornar ao radar a fase será: = o + 4 r/ d d o

Portanto, a mudança de fase em função do tempo (de um pulso a outro) pode ser expressa como, a variação temporal da fase no tempo, ou seja:

• mas como a velocidade radial é • e a frequência angular é Logo, Lembrando que = 2 f (onde f é a mudança de frequência em ciclos por segundo, Hz) temos que:

• Como o comprimento de onda é cte, isso implica que a mudança de frequência é linearmente proporcional à velocidade de propagação do alvo. • Como a variação da frequência é sempre perpendicular ao feixe, temos que o radar meteorológico mede a velocidade radial.

• Com o aumento da velocidade do alvo, a mudança de fase também aumenta. • Entretanto existe um limite para a mudança de fase que o radar pode detectar.

Por exemplo, se um alvo estivesse se distanciando do radar a um velocidade, V = ½ entre 2 consecutivos pulsos, a fase seria igual a , e se estivesse se movendo em direção ao radar a fase também seria , logo temos uma ambiguidade Por outro lado, se o alvo estivesse se propagando a uma velocidade V = , a fase seria 0 e o alvo estaria estacionário.
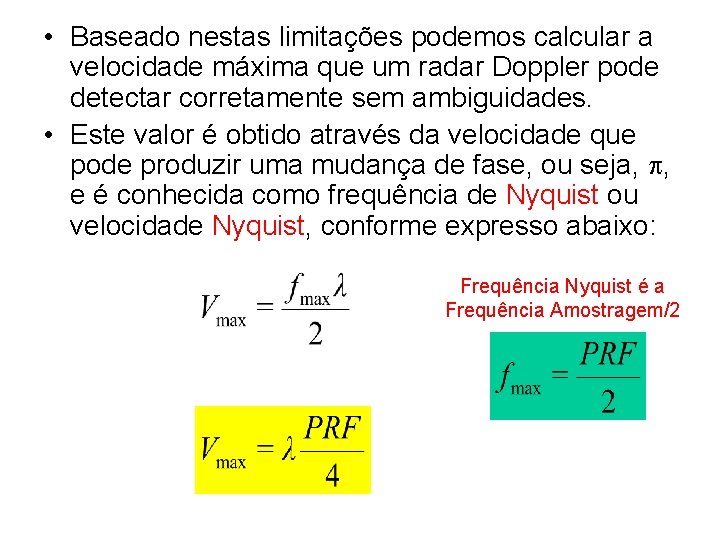
• Baseado nestas limitações podemos calcular a velocidade máxima que um radar Doppler pode detectar corretamente sem ambiguidades. • Este valor é obtido através da velocidade que pode produzir uma mudança de fase, ou seja, , e é conhecida como frequência de Nyquist ou velocidade Nyquist, conforme expresso abaixo: Frequência Nyquist é a Frequência Amostragem/2
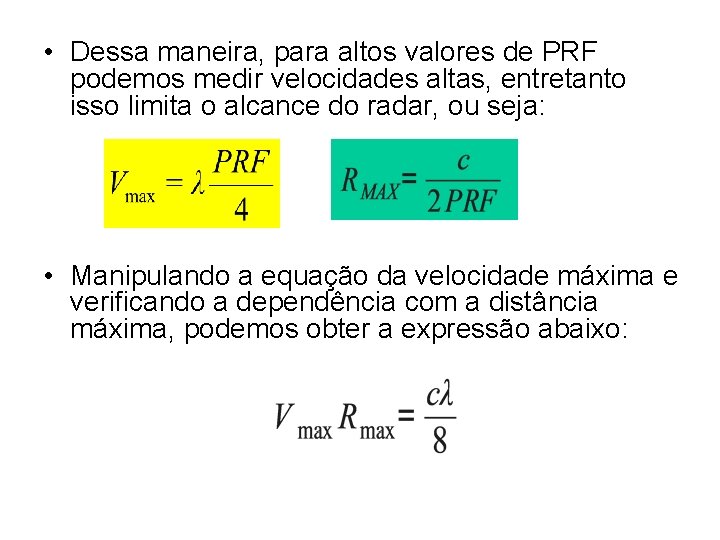
• Dessa maneira, para altos valores de PRF podemos medir velocidades altas, entretanto isso limita o alcance do radar, ou seja: • Manipulando a equação da velocidade máxima e verificando a dependência com a distância máxima, podemos obter a expressão abaixo:

Para medirmos velocidades altas, temos que reduzir o alcance do radar Por exemplo: PRF = 1000 Hz e alcance de 150 km Banda S V max = 25 m/s Banda X V max = 8 m/s
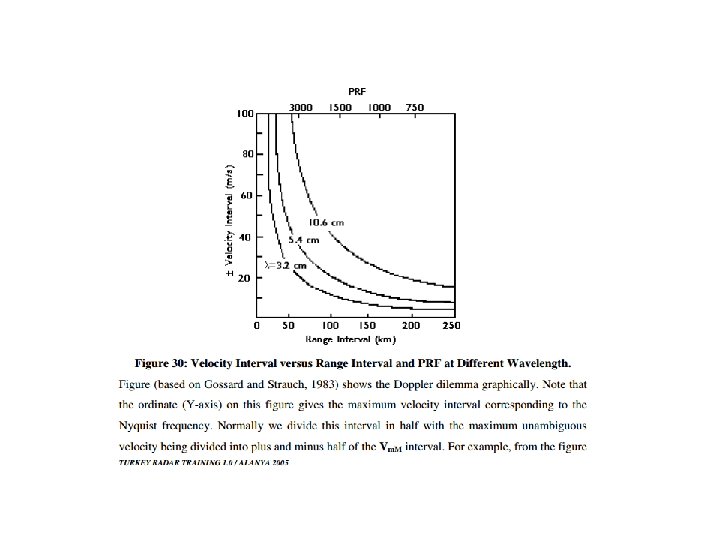

Por convenção, as velocidade positivas significam que os alvos estão se distanciando do radar, enquanto que as negativas estão se aproximando.
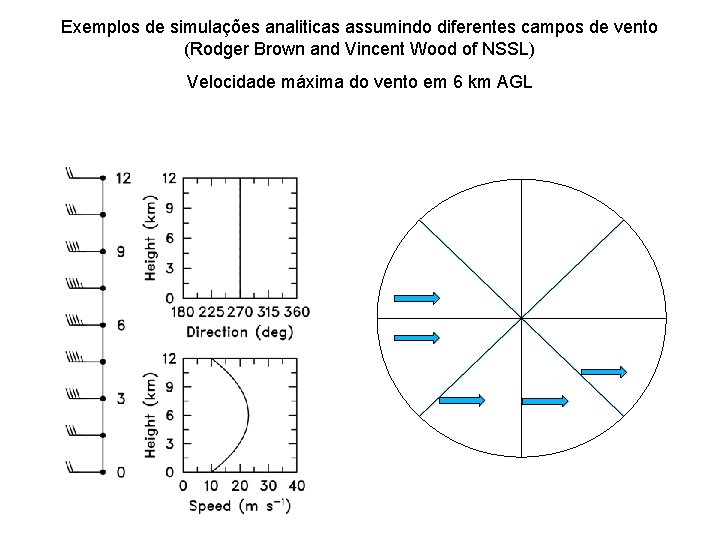
Exemplos de simulações analiticas assumindo diferentes campos de vento (Rodger Brown and Vincent Wood of NSSL) Velocidade máxima do vento em 6 km AGL
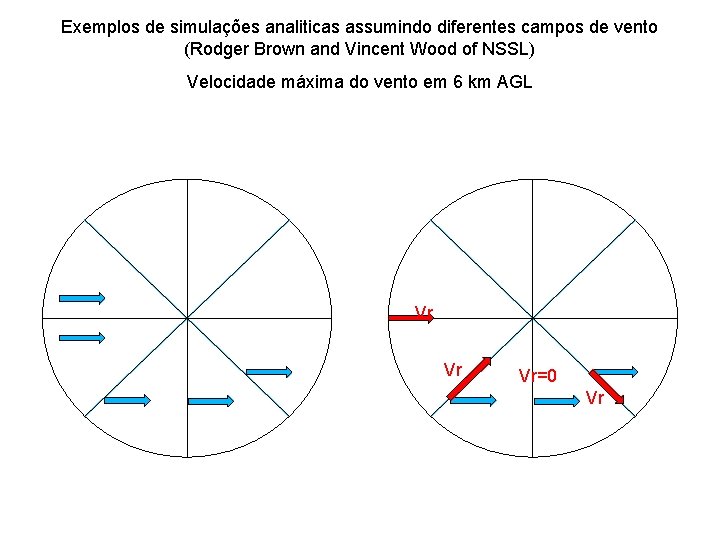
Exemplos de simulações analiticas assumindo diferentes campos de vento (Rodger Brown and Vincent Wood of NSSL) Velocidade máxima do vento em 6 km AGL Vr Vr Vr=0 Vr
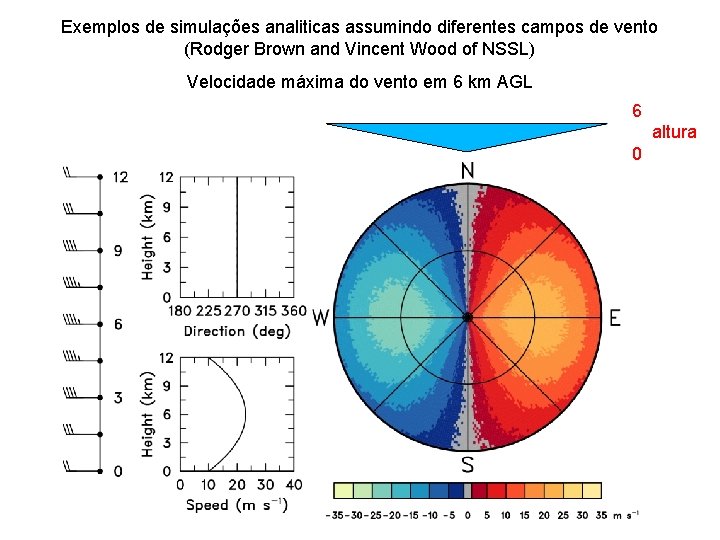
Exemplos de simulações analiticas assumindo diferentes campos de vento (Rodger Brown and Vincent Wood of NSSL) Velocidade máxima do vento em 6 km AGL 6 altura 0
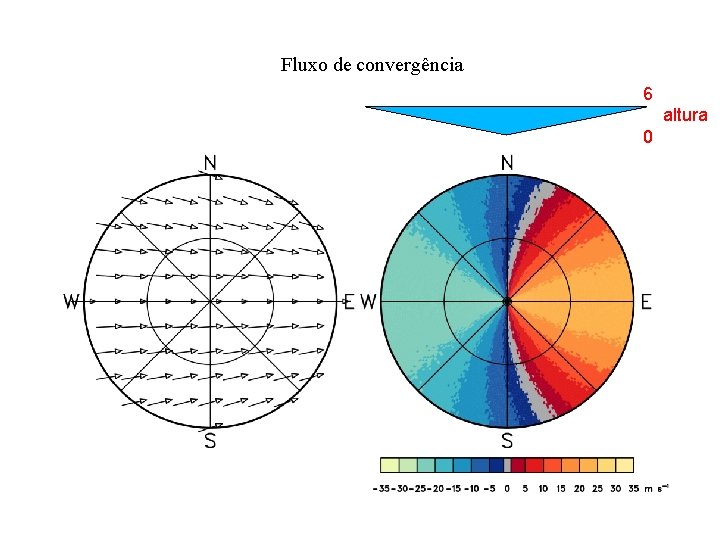
Fluxo de convergência 6 altura 0
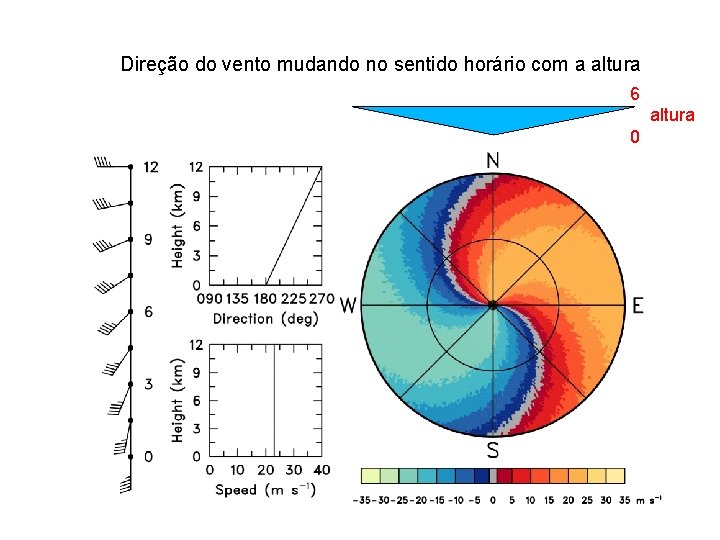
Direção do vento mudando no sentido horário com a altura 6 altura 0
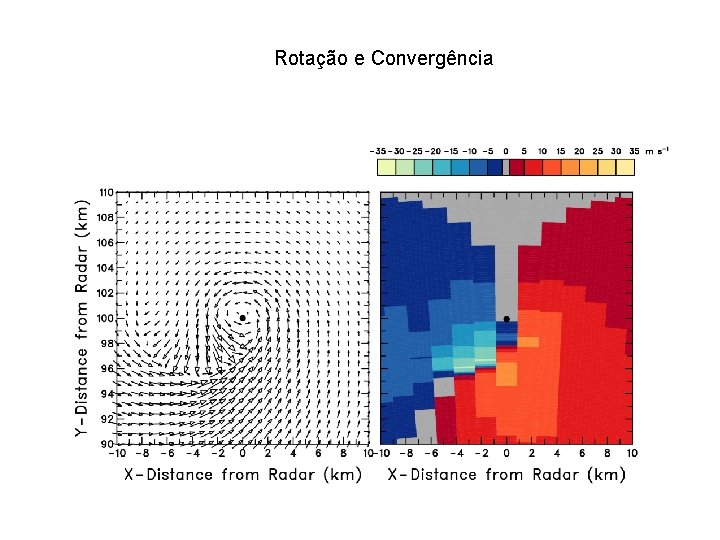
Rotação e Convergência
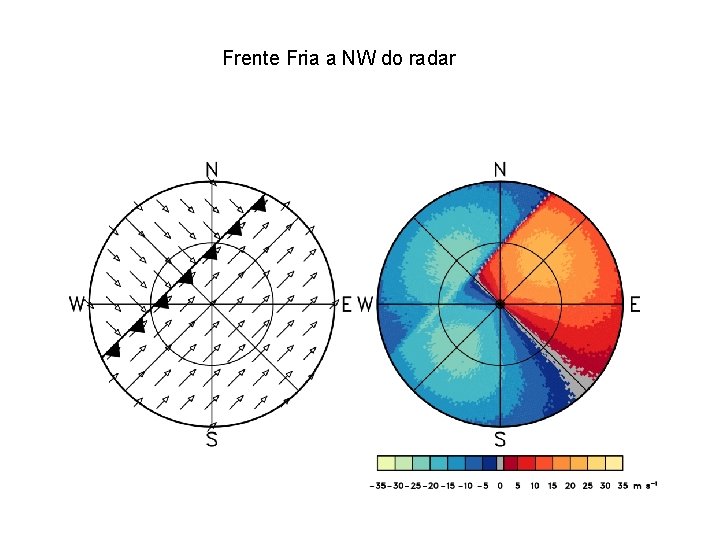
Frente Fria a NW do radar

Velocidade Ambígua
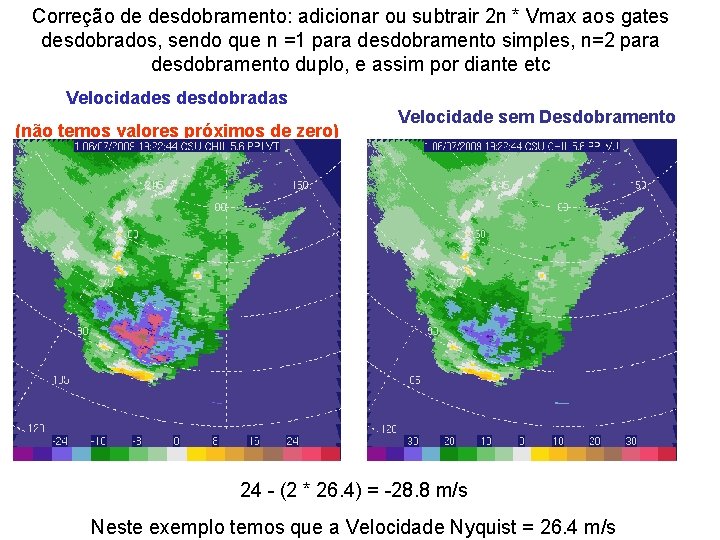
Correção de desdobramento: adicionar ou subtrair 2 n * Vmax aos gates desdobrados, sendo que n =1 para desdobramento simples, n=2 para desdobramento duplo, e assim por diante etc Velocidades desdobradas (não temos valores próximos de zero) Velocidade sem Desdobramento 24 - (2 * 26. 4) = -28. 8 m/s Neste exemplo temos que a Velocidade Nyquist = 26. 4 m/s

Neste exemplo a velocidade Nyquist é 26. 4 m/s. Desdobramento

Se o radar dispor de medidas com Dupla Frequência, é possível aumentar a velocidade de Nquist. Basicamente, além da variação de fase obtida por uma feixe que tem uma PRF, podemos também analisar a diferença de fase entre dois feixes consecutivos que tem diferentes PRF. De acordo com (Dazhang et al. , 1984), a velocidade máxima em modo de Dupla PRF pode ser expressa como: Onde, N é de vezes que se quer Aumentar. Dazhang, T. , S. G. Geotis, R. E. Passarelli Jr. , A. L. Hansen, and C. L. Frush: 1984, Evaluation of an Alternating-PRF Method for Extending the Range of Unambiguous Doppler Velocity. 22 nd conference on Radar Meteorology, Zurich, ¨ Switzerland, Amer. Meteor. Soc. , 523– 527

Por exemplo: N = 2, e PRFalta = 1000 Hz e = 10 cm ~2 X
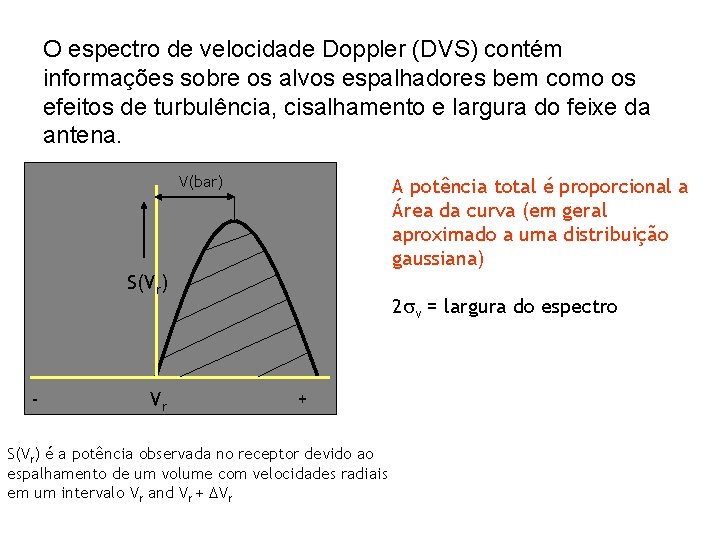
O espectro de velocidade Doppler (DVS) contém informações sobre os alvos espalhadores bem como os efeitos de turbulência, cisalhamento e largura do feixe da antena. V(bar) A potência total é proporcional a Área da curva (em geral aproximado a uma distribuição gaussiana) S(Vr) - Vr 2 v = largura do espectro + S(Vr) é a potência observada no receptor devido ao espalhamento de um volume com velocidades radiais em um intervalo Vr and Vr + Vr
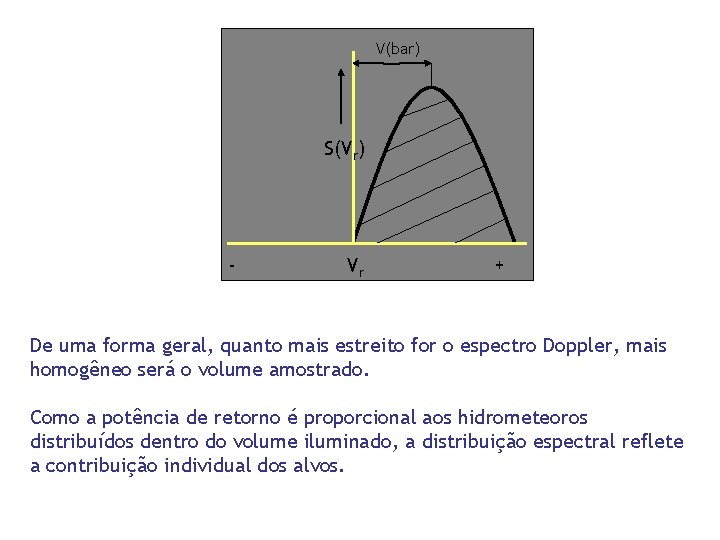
V(bar) S(Vr) - Vr + De uma forma geral, quanto mais estreito for o espectro Doppler, mais homogêneo será o volume amostrado. Como a potência de retorno é proporcional aos hidrometeoros distribuídos dentro do volume iluminado, a distribuição espectral reflete a contribuição individual dos alvos.
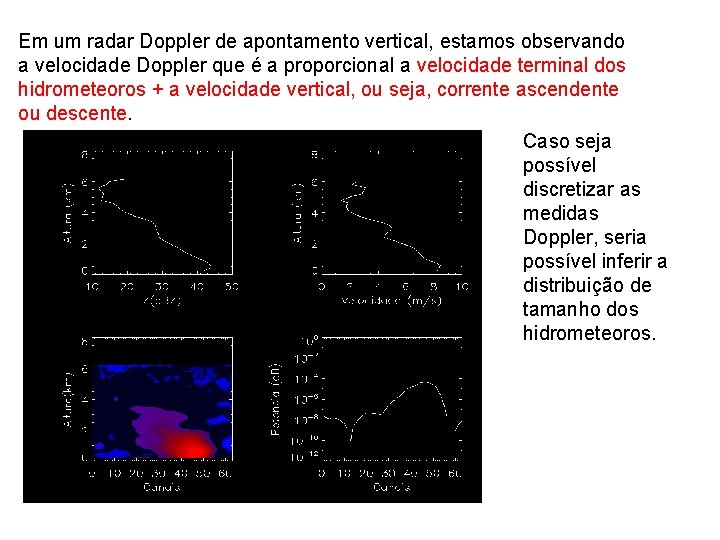
Em um radar Doppler de apontamento vertical, estamos observando a velocidade Doppler que é a proporcional a velocidade terminal dos hidrometeoros + a velocidade vertical, ou seja, corrente ascendente ou descente. Caso seja possível discretizar as medidas Doppler, seria possível inferir a distribuição de tamanho dos hidrometeoros.

Já que temos uma relação entre a potência e a refletividade (eq. do radar), o espectro de velocidade Doppler (DVS) pode ser pensado como sendo a refletividade ponderada pela distribuição de velocidades radiais em um volume pulsado (i. e. velocidade radial ponderada pelo D 6) Potência do Sinal Pr Para alvos precipitantes, S 0 está relacionado com a refletividade do radar e contém informações sobre a DSD.

Vel. Radial Média Análogo ao centro de massa de uma distribuição tipo dente de serra Largura Espectral Controlada pela turbulência, cisalhamento e largura da antena, vel. Terminal característica dos espalhadores dentro do volume pulsado
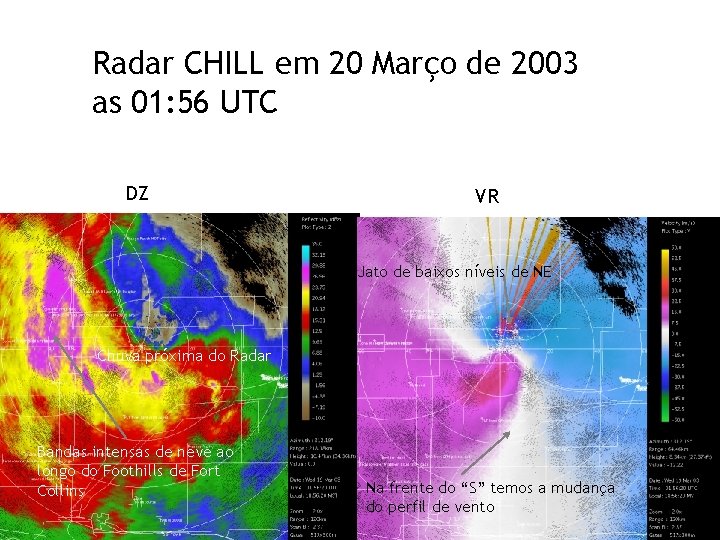
Radar CHILL em 20 Março de 2003 as 01: 56 UTC DZ VR Jato de baixos níveis de NE Chuva próxima do Radar Bandas intensas de neve ao longo do Foothills de Fort Collins Na frente do “S” temos a mudança do perfil de vento

Observações do CHILL durante uma super-célula e tornado DZ Gates: 1034 e 150 m Zoom: 4 x Desenvolvimento de um gancho VR Assinatura de um tornado
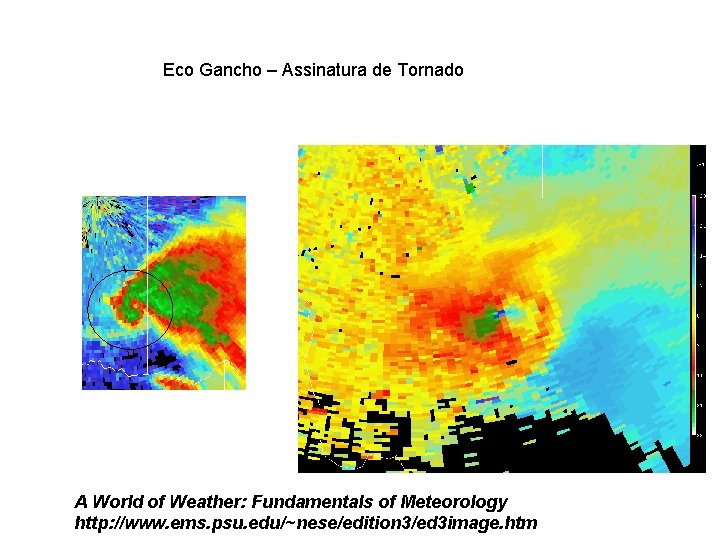
Eco Gancho – Assinatura de Tornado A World of Weather: Fundamentals of Meteorology http: //www. ems. psu. edu/~nese/edition 3/ed 3 image. htm
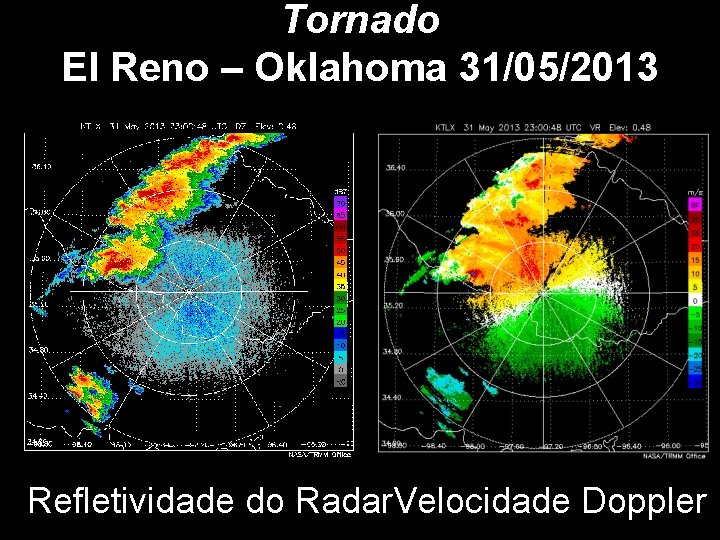
Tornado El Reno – Oklahoma 31/05/2013 Refletividade do Radar. Velocidade Doppler
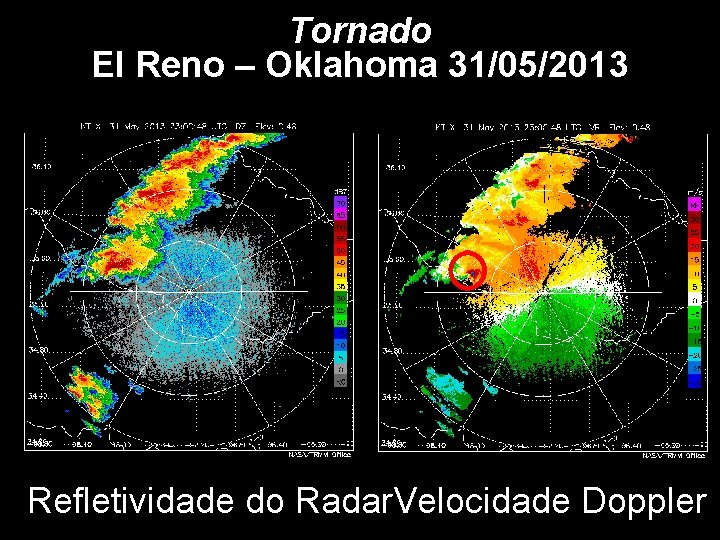
Tornado El Reno – Oklahoma 31/05/2013 Refletividade do Radar. Velocidade Doppler
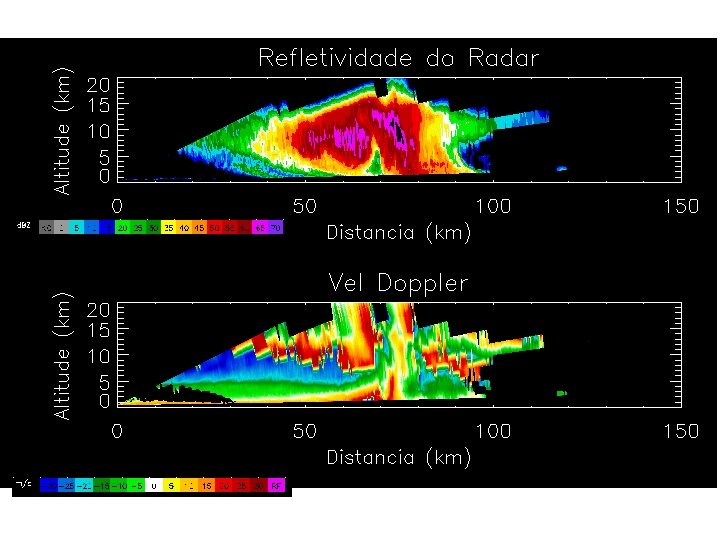

Tornado Brasília: 1 de Out 2014 www. ebc. com. br
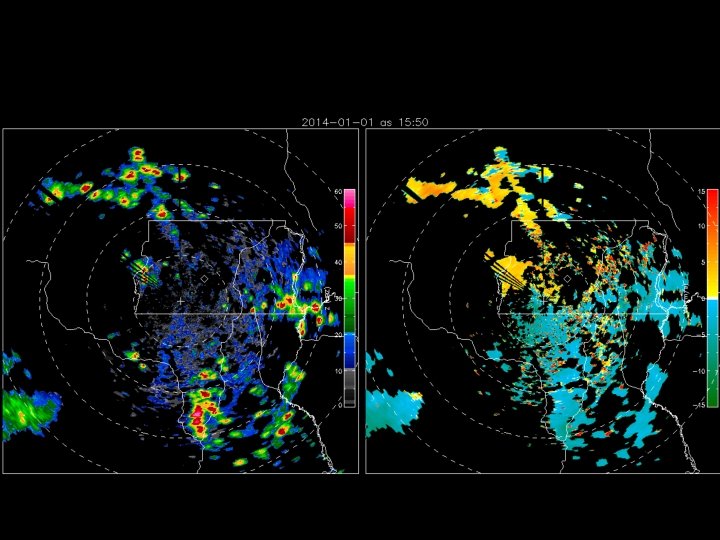
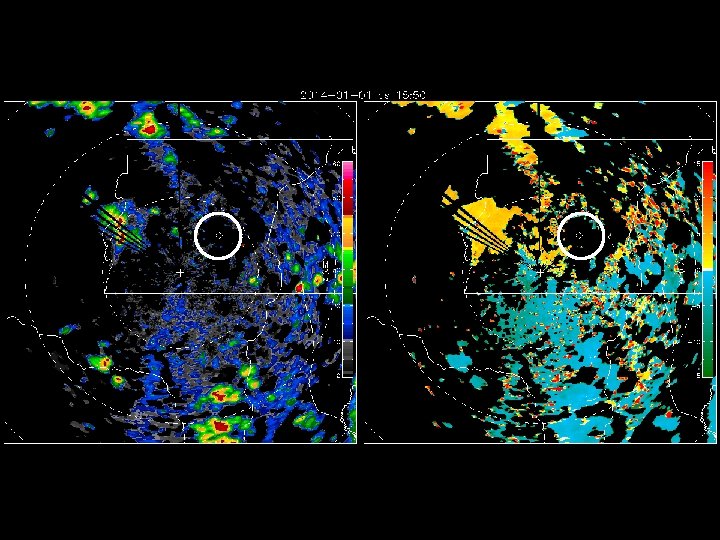
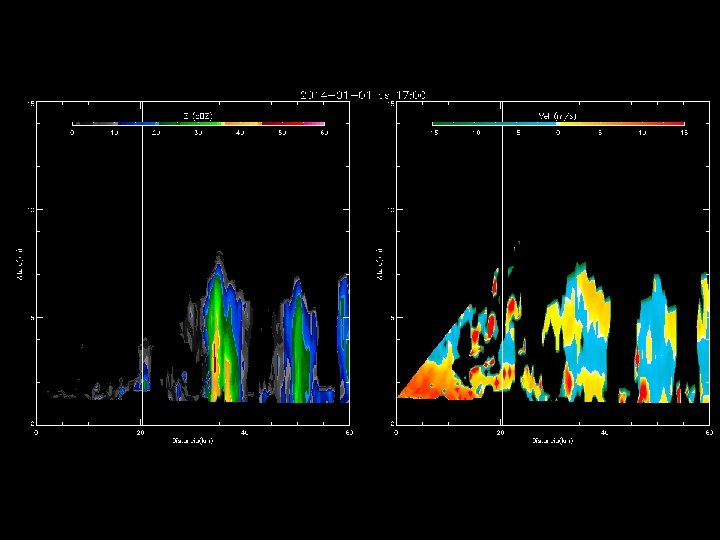
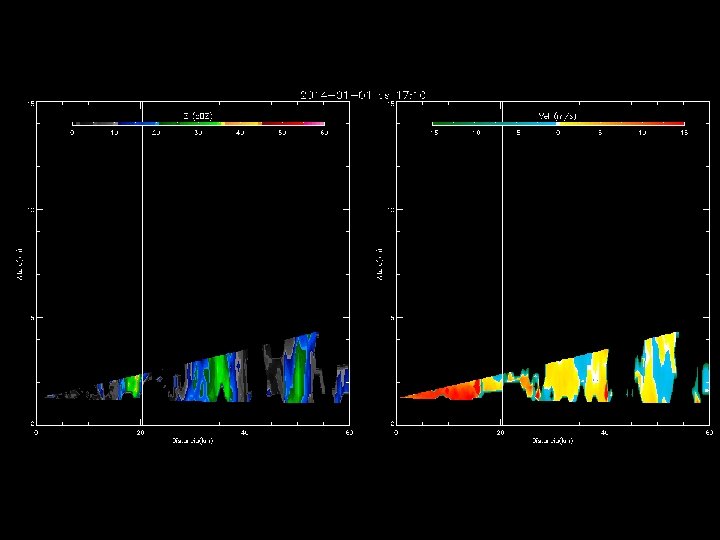
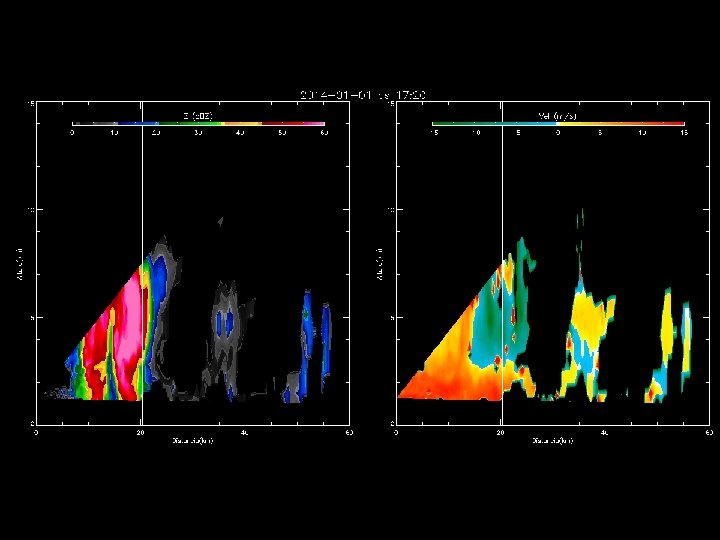
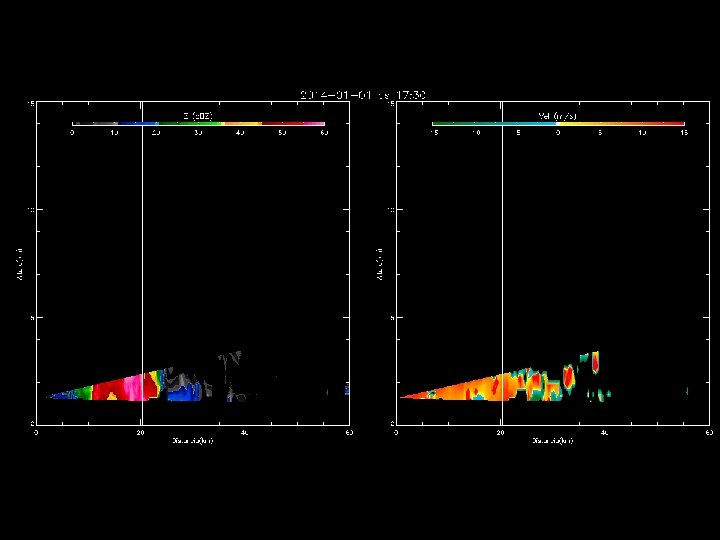
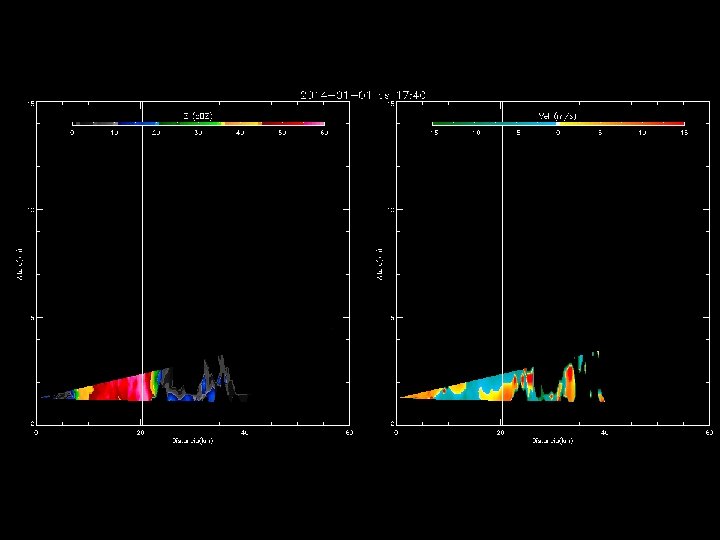
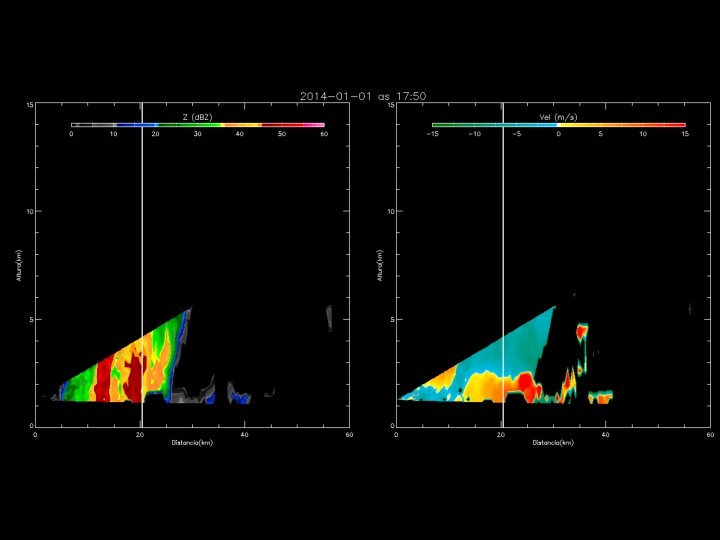

Outras aplicações de um Radar Doppler
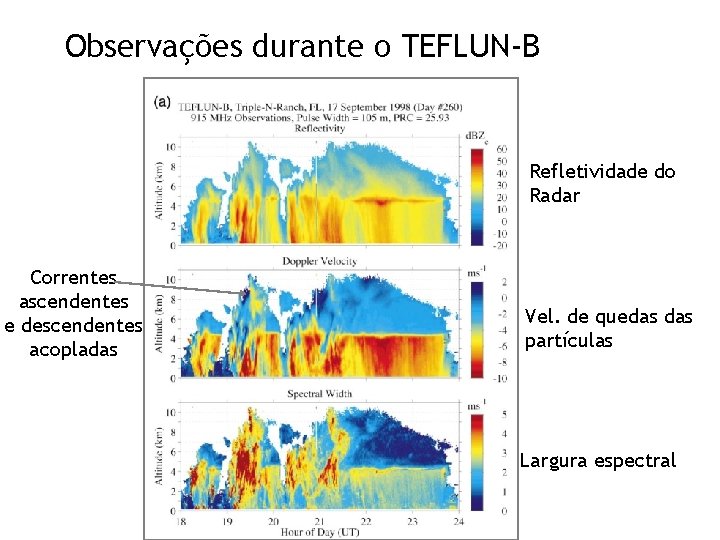
Observações durante o TEFLUN-B Refletividade do Radar Correntes ascendentes e descendentes acopladas Vel. de quedas partículas Largura espectral

Relação entre a VT e Refletividade O movimento das partículas observado pelo radar é a somatória das velocidades terminais de cada partícula (VT) e o movimento do ar (w): VP = w-VT (como convenção, vel. negativas indicam movimento p/ o radar) Se VT pode ser estimado indiretamente, a equação acima pode ser utilizada para obter a solução de w. Quais outras observações do radar podem ser utilizadas para determinar VT? Temos que lembrar que a velocidade radial média refletividade ponderada pela velocidade doppler éa

De forma análoga a Rogers 1964, VT pode ser definido como a refletividade ponderada pela velocidade de queda: Usando V(D) = a. Db (p 0/p)0. 4 e N(D) = N 0 exp{- D}

Integrando, temos: Lembrando que para uma DSD exponencial, o fator refletividade do radar (Z) pode ser expresso como: Substituindo, temos: A qual nos leva a uma equação na forma de

Exemplos de relações disponíveis na literatura sendo que está em m/s e Z em mm 6/m 3 Assumindo a DSD de MP - N(D) = N 0 exp{- D} onde N 0 = 0. 08 cm-4, = 41 R{-0. 21} Para tempestades : (Sekhon e Srivastava 1971) (Joss e Waldvogel 1970)
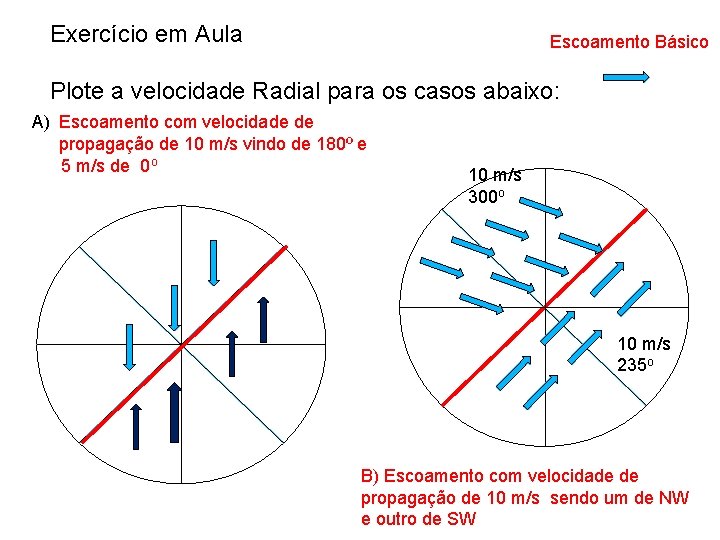
Exercício em Aula Escoamento Básico Plote a velocidade Radial para os casos abaixo: A) Escoamento com velocidade de propagação de 10 m/s vindo de 180º e 5 m/s de 0 o 10 m/s 300 o 10 m/s 235 o B) Escoamento com velocidade de propagação de 10 m/s sendo um de NW e outro de SW
- Slides: 53