Medidas de disperso Desvio mdio Desviopadro Varincia Estatstica

Medidas de dispersão: • Desvio médio, • Desvio-padrão • Variância Estatística Aplicada 2º Ano – Ensino Subsequente Prof. André Aparecido da Silva E-mail: anndrepr@yahoo. com. br

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância INTRODUÇÃO Há situações em que as medidas de tendência central - Média, Moda e Mediana - não suficientes para caracterizar uma determinada coleta de dados.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância INTRODUÇÃO (CONTINUAÇÃO) Nesse caso, é conveniente utilizar as medidas de dispersão: desvio médio, desvio padrão e variância, pois expressam o grau de dispersão de um conjunto de dados.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância MÉDIA ARITMÉTICA (MA) A média aritmética de um conjunto de dados numéricos é obtida somando-se os valores de todos os dados e dividindo -se essa soma pelo número de dados apresentados.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância MÉDIA ARITMÉTICA (MA) Por exemplo: Qual a média aritmética entre os números: 2, 4, 6, 8 e 10?

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO (MA)

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância MEDIDAS DE DISPERSÃO DESVIO MÉDIO, VARI NCIA E DESVIO PADRÃO

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância Para compreendermos melhor esses conceitos relativos à Estatística, vamos explicá-los a partir da seguinte situaçãoproblema:

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SITUAÇÃO-PROBLEMA Considere a distribuição numérica cujos resultados constam na lista abaixo: 1, 6, 4, 10, 9

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância MÉDIA ARITMÉTICA A média aritmética dessa distribuição 1, 6, 4, 10, 9 é: MA = (1 + 6 + 4 + 10 + 9)/5 MA = 30/5 MA = 6 A média aritmética é 6.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância MÉDIA / DESVIO Chama-se DESVIO de cada valor apresentado a diferença entre esse valor e a média aritmética desses valores. Na situação anterior, a distribuição é 1, 6, 4, 10, 9, e a média aritmética é 6. Portanto, temos:

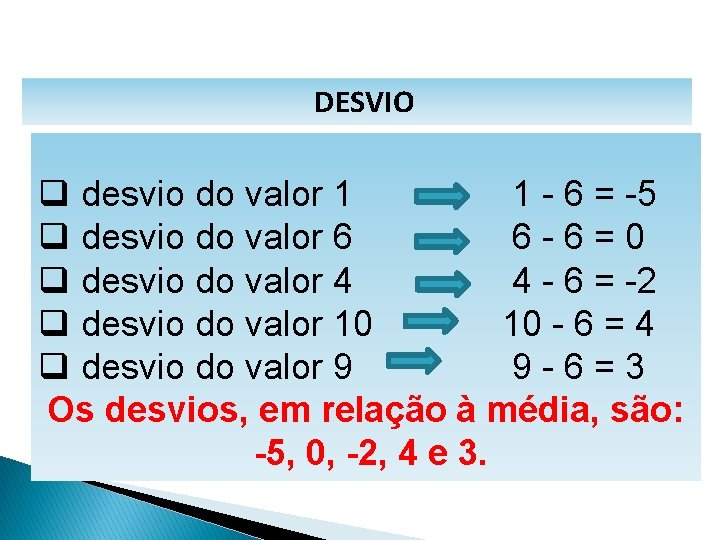
MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância DESVIO q desvio do valor 1 1 - 6 = -5 q desvio do valor 6 6 -6=0 q desvio do valor 4 4 - 6 = -2 q desvio do valor 10 10 - 6 = 4 q desvio do valor 9 9 -6=3 Os desvios, em relação à média, são: -5, 0, -2, 4 e 3.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância A partir da situação com a distribuição dos números 1, 6, 4, 10, 9, considerando que a média aritmética entre eles é igual a 6 e que os desvios, em relação à média, são -5, 0, -2, 4 e 3. . .

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância . . . vamos definir as medidas de dispersão: desvio médio, variância e desvio padrão.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância DESVIO MÉDIO

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância Chama-se desvio médio (DM) de uma distribuição a média aritmética dos módulos desvios. No exemplo em análise, os desvios são -5, 0 -2, 4 e 3, logo o desvio médio será:

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância Formula desvio médio

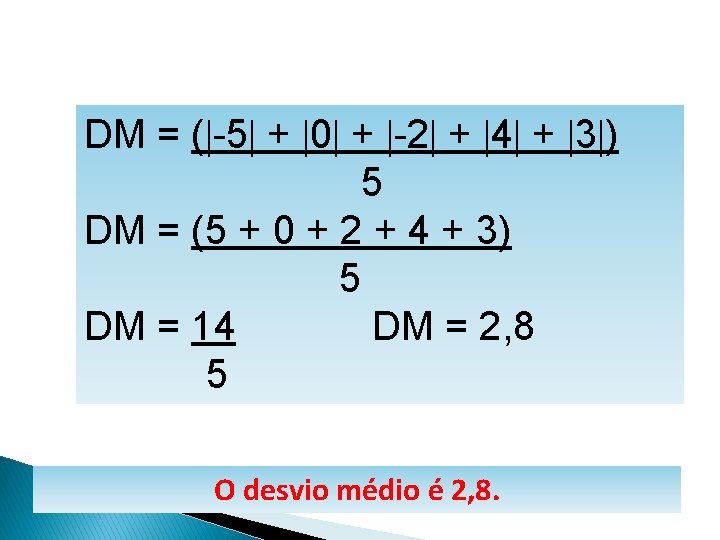
MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância DM = ( -5 + 0 + -2 + 4 + 3 ) 5 DM = (5 + 0 + 2 + 4 + 3) 5 DM = 14 DM = 2, 8 5 O desvio médio é 2, 8.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância O módulo garante que o valor seja positivo. EX: a) +3 = 3 b) -3 = 3

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância VARI NCIA

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância Chama-se variância (V) de uma distribuição a média aritmética dos quadrados desvios dessa distribuição. Na situação em análise, os desvios são -5, 0 -2, 4 e 3, logo a variância será:

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância V = ((-5)² + (0)² + (-2)² + (4)² + (3)²). 5 V = (25 + 0 + 4 + 16 + 9) 5 V = 54 V = 10, 8 5 A variância é 10, 8.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância DESVIO PADRÃO

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância Chama-se desvio padrão (DP) de uma distribuição a raiz quadrada da variância:

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância No exemplo em análise, temos que a variância é 10, 8, portanto o desvio padrão será: DP = 10, 8 3, 28. O desvio padrão é 3, 28.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância O desvio padrão. . .

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância OBSERVAÇÕES: q Quando todos os valores de uma distribuição forem iguais, o desvio padrão será igual a zero;

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância OBSERVAÇÕES: q Quanto mais próximo de zero for o desvio padrão, mais homogênea será a distribuição dos valores;

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância OBSERVAÇÕES: q o desvio padrão é expresso na mesma unidade distribuídos. dos valores

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância EXERCÍCIOS DE FIXAÇÃO 1º) Considerando a distribuição dos números 2, 4, 6 e 10, determine: a) o desvio médio; b) a variância; c) o desvio padrão.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO - MÉDIA A distribuição é 2, 4, 6 e 12, então temos: MA = (2+4+6+12) MA = 24 M = 6 4 4

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO (DESVIO MÉDIO) A distribuição é 2, 4, 6 e 12, então temos: DM = ( 2 -6 + 4 -6 + 6 -6 + 12 -6 ) 4 DM = |-4|+|2|+|0|+|6| =

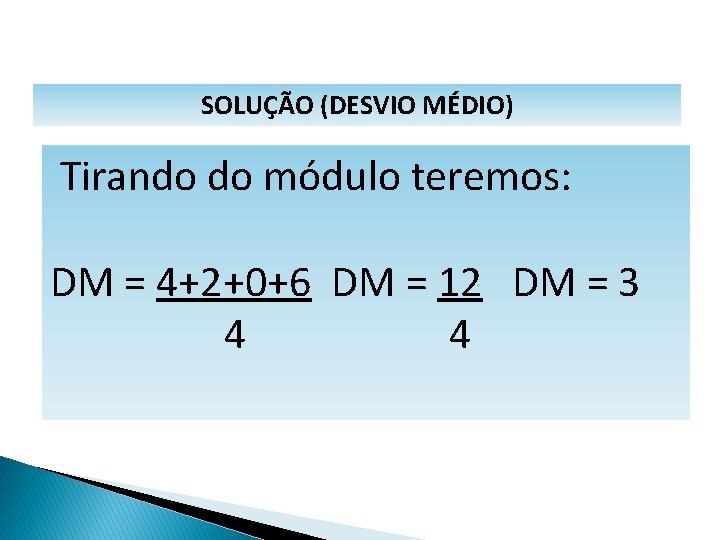
MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO (DESVIO MÉDIO) Tirando do módulo teremos: DM = 4+2+0+6 DM = 12 DM = 3 4 4

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância VARI NCIA - SOLUÇÃO A distribuição é 2, 4, 6 e 12, então temos: V = ((2 -6)² + (4 -6)² + (6 -6)² + (12 -6)²) 4 V = (-4)² + (2)² + 0² + 6² 4

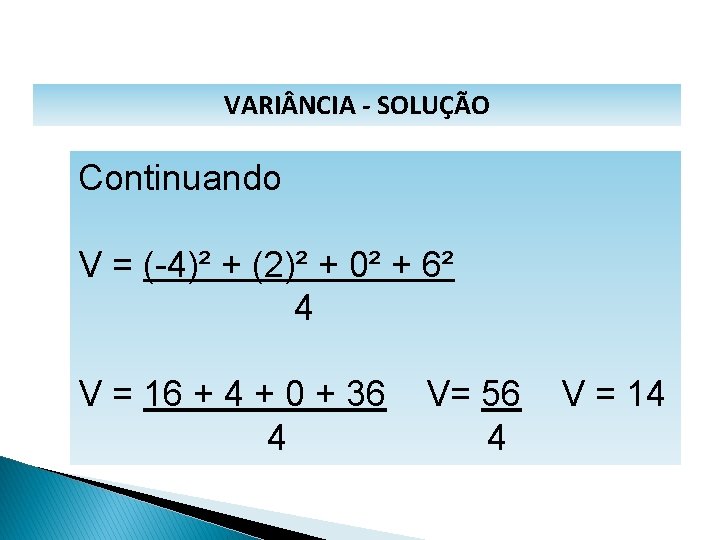
MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância VARI NCIA - SOLUÇÃO Continuando V = (-4)² + (2)² + 0² + 6² 4 V = 16 + 4 + 0 + 36 4 V= 56 4 V = 14

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO – DESVIO PADRÃO A distribuição é 2, 4, 6 e 12, então temos: c) DP = 14 = 3, 74

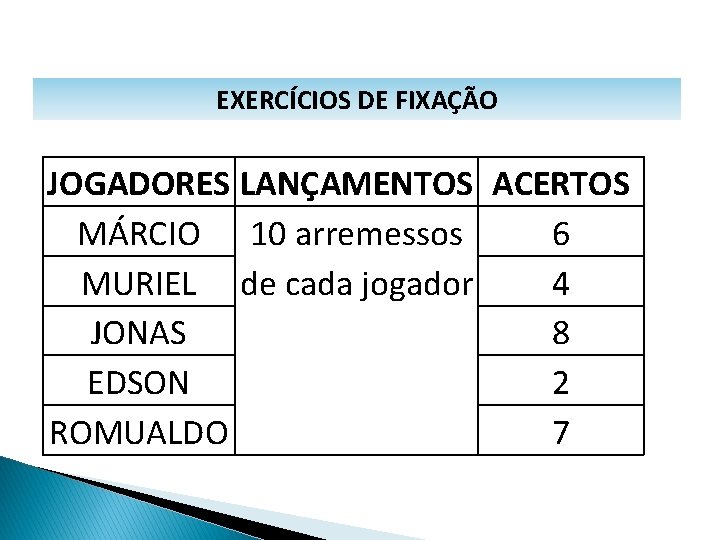
MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância EXERCÍCIOS DE FIXAÇÃO 2º) Em um jogo de arremessos, coletaram-se os dados da tabela a seguir. Dessa forma, em relação aos acertos, determine: a) a média aritmética; b) o desvio médio; c) a variância; d) o desvio padrão.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância EXERCÍCIOS DE FIXAÇÃO JOGADORES LANÇAMENTOS ACERTOS MÁRCIO 10 arremessos 6 MURIEL de cada jogador 4 JONAS 8 EDSON 2 ROMUALDO 7

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO a) MA = (6+4+8+2+7)/5 = 27/5 = 5, 4 b) DM = ( 6 -5, 4 + 4 -5, 4 + 8 -5, 4 + 2 -5, 4 + 7 -5, 4 )/5 DM = 1, 92 c) V = ((6 -5, 4)² + (4 -5, 4)² + (8 -5, 4)² + (2 -5, 4)² + (7 -5, 4)²)/5 V = 4, 64 d) DP = 4, 64 = 2, 15

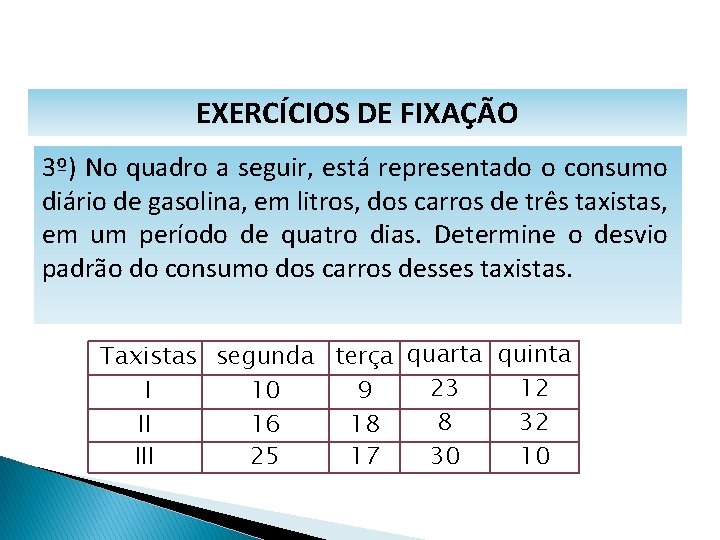
MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância EXERCÍCIOS DE FIXAÇÃO 3º) No quadro a seguir, está representado o consumo diário de gasolina, em litros, dos carros de três taxistas, em um período de quatro dias. Determine o desvio padrão do consumo dos carros desses taxistas. Taxistas segunda terça quarta quinta 23 12 I 10 9 8 32 II 16 18 III 25 17 30 10

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO Para determinarmos o desvio padrão, precisaremos, antes, calcular a média aritmética e a variância. Calculando a média aritmética de consumo dos carros dos três taxistas, temos: MAI = (10+9+23+12)/4 = 13, 5 MAII = (16+18+8+32)/4 = 18, 5 MAIII = (25+17+30+10)/4 = 20, 5

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO Agora, vamos calcular a variância para o consumo dos carros dos três taxistas. VI = [(10 -13, 5)²+(9 -13, 5)²+(23 -13, 5)²+(12 -13, 5)²]/4 31, 25 VII = [(16 -18, 5)²+(18 -18, 5)²+(32 -18, 5)²]/4 74, 75 VIII = [(25 -20, 5)²+(17 -20, 5)²+(30 -20, 5)²+(10 -20, 5)²]/4 58, 25 Observando a variância, notamos que o carro do taxista II tem a maior dispersão em relação aos demais, e o carro do taxista I tem a menor dispersão.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO Finalmente, vamos calcular o desvio padrão e analisar o consumo dos carros dos três taxistas. DPI = 31, 25 5, 59 litros DPII = 74, 75 8, 64 litros DPIII = 58, 25 7, 63 litros Pela análise do desvio padrão, verifica-se que o carro do taxista I teve o consumo mais regular em torno da média, pois seu desvio padrão é o menor.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância EXERCÍCIOS DE FIXAÇÃO 4º) Ao procurar emprego, um rapaz teve que optar por duas ofertas dispostas em um jornal, como mostra a tabela a seguir. Qual das ofertas representa a melhor opção? Por quê? Oferta 1 Oferta 2 Média Salarial 890, 00 950, 00 Mediana 800, 00 700, 00 Desvio Padrão 32, 00 38, 00

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância SOLUÇÃO Pela definição do desvio padrão, sabemos que quanto menor o DP, mais homogêneos serão os valores, ou seja, a diferença entre eles é mínima. Dessa forma, a oferta 1 é a mais vantajosa, por ter o menor desvio padrão.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância REFERÊNCIAS BIBLIOGRÁFICAS q. DANTE, Luiz Roberto. Matemática, volume único. 1ª edição. Ática. São Paulo, 2005. q IEZZI, Gelson. . . [et al], Matemática: ciência e aplicações, 1ª série, Ensino Médio. Atual, São Paulo, 2004. q GUELLI, Oscar. Matemática, volume único. 1ª edição. Ática. São Paulo, 2003. q PAIVA, Manoel. Matemática, volume único. 1ª edição, Moderna. São Paulo, 1999.

MATEMÁTICA, 1º Ano Medidas de dispersão: desvio médio, desvio padrão e variância Disponível em: www. oxnar. com. br