MATRSLERN TANIMI MATRSLERDE TOPLAMA LEM SATIR MATRS TOPLAMA

MATRİSLERİN TANIMI MATRİSLERDE TOPLAMA İŞLEMİ SATIR MATRİS TOPLAMA İŞLEMİNİN ÖZELLİKLERİ SÜTUN MATRİS KARE MATRİS SIFIR MATRİS KÖŞEGEN MATRİS VE SKALER MATRİS BİRİM MATRİS İKİ MATRİSİN EŞİTLİĞİ MATRİSİN SKALARLA ÇARPIMI MATRİSLERDE ÇARPMA İŞLEMİNİN ÖZELLİKLERİ BİR MATRİSİN ÇARPMA İŞLEMİNE GÖRE TERSİ BİR MATRİSİN TRANSPOZU (DEVRİĞİ)

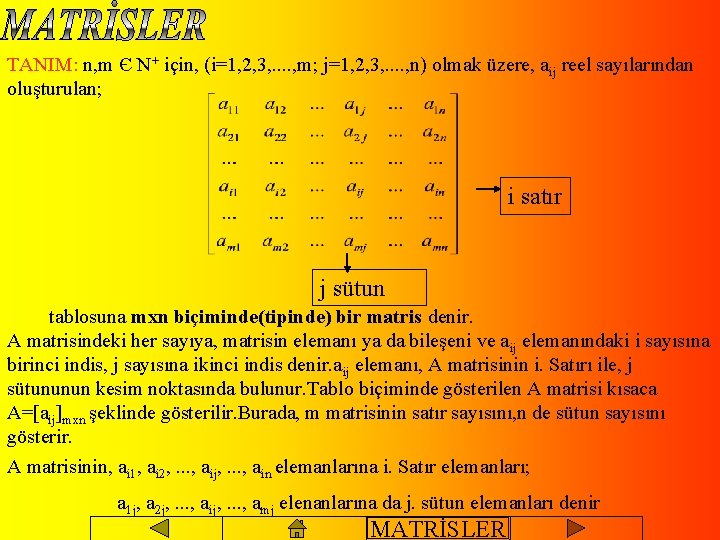
TANIM: n, m Є N+ için, (i=1, 2, 3, . . , m; j=1, 2, 3, . . , n) olmak üzere, aij reel sayılarından oluşturulan; i satır j sütun tablosuna mxn biçiminde(tipinde) bir matris denir. A matrisindeki her sayıya, matrisin elemanı ya da bileşeni ve aij elemanındaki i sayısına birinci indis, j sayısına ikinci indis denir. aij elemanı, A matrisinin i. Satırı ile, j sütununun kesim noktasında bulunur. Tablo biçiminde gösterilen A matrisi kısaca A=[aij]mxn şeklinde gösterilir. Burada, m matrisinin satır sayısını, n de sütun sayısını gösterir. A matrisinin, ai 1, ai 2, . . . , aij, . . . , ain elemanlarına i. Satır elemanları; a 1 j, a 2 j, . . . , aij, . . . , amj elenanlarına da j. sütun elemanları denir MATRİSLER

Tanım: A=[aij]mxn matrisinin her satırına, satır matrisi(satır vektörü) denir. B 1=[a 11 a 12. . . a 1 n] (1. satır matrisi) B 2=[a 21 a 22. . . a 2 n] (2. satır matrisi) Bm=[am 1 am 2. . . amn] (m. satırmatrisi) A matrisi satır matrisine bağlı olarak, A=[aij]mxn= şeklinde gösterilir MATRİSLER

Tanım: A=[aij]mxn matrisinin her sütununa, sütun matrisi(sütun vektörü)denir , , . . . , A 1: birincisütun matrisi A 2: ikinci sütun matrisi. . . An: n. Sütun matrisi A matrisi sütun matrislerine bağlı olarak, A=[aij]mxn=[A 1 A 2 A 3. . . An] şeklinde gösterilir. MATRİSLER

Tanım: Nxn tipindeki[aij]nxn matrisine, n. sırada kare matris denir. Örneğin; Matrisi, 2. sıradan bir kare matristir. MATRİSLER

Tanım: Bütün elemanları sıfır olan matrise, sıfır matrisi denir ve O harfi ile gösterilir Örneğin; Matrisi. 2 x 3 tipinde sıfır matrisidir. Tanım: [aij]nxn kare matrisinde a 11 , a 22 , a 33 , . . . , ann elemanlarının oluşturduğu köşegene, asal köşegen; an 1 , a(n-1)2 , . . . , a 1 n terimlerinin oluşturduğu köşegene, yedek köşegen denir. Yedek köşegen Asal köşegen MATRİSLER

Tanım: A=[AİJ]nxn kare matrisinde asal köşegen üzerindeki elemanların dışında, diğer elemanları sıfır ise, bu tip matrise, köşegen matris denir. matrisi, 3. sıradan bir köşegen matrisidir. Tanım: A=[aij]nxn köşegen matrisinde a 11=a 22=. . . =ann=k ise, (kЄR) bu matrise, skalar matris denir. Matrisi, 2. sıradan bir skalar matrisidir. MATRİSLER

Tanım: Asal köşegen üzerindeki elemanları bir, diğer elemanları sıfır olan kare matrise, birim matris denir. In şeklinde gösterilir. matrisi, 4. sıradan birim matrisidir. Asal eksen MATRİSLER

Tanım: asal köşegen üzerindeki elemanları eşit olan matrislere, eşit matrisler denir. Örnek: ve olmak üzere, A=B ise, kaçtır? Çözüm: A=B = matrisinin eşitliğinden, 5 a=4, 5 b=2, 3 a+2 b=x, a+2 b=y olduğundan 5 a=22 5 b=2 5 a=52 b den, a=2 b olur. Bulunan değer de 52 b=22 yerine yazılırsa; = = = MATRİSLER

Tanım: A=[aij]mxn ve. B=[bij]mxn matrisleri verilmiş olsun. A+B=[aij]+[bij]mxn=[aij+bij]mxn matrisine, A ve B matrislerinin toplamı denir. Örnek: olması için (a, b) ikilisi ne olmalıdır? Çözüm: Verilen eşitliğin birinci yanındaki matrisleri toplarsak, elde edilir. Bu eşitlikten, A-2 b=-11 2 a+b=-1 Denklemleri yazılır. Bu denklemler çözülürse, (a, b)=(-2, 3) bulunur MATRİSLER

1. Değişme özelliği vardır. A+B=B+A 2. Birleşme özelliği vardır. A+(B+C)=(A+B)+C 3. Sıfır matris, etkisiz elemandır. A+0=A 4. A=[aij]mxn matrisinin toplama işlemine göre ters matrisi, -A=[-aij]mxn matrisidir. 5. İki matris farkı; A-B=A-(B) MATRİSLER

C bir sayı olmak üzere, bu cismin elemanlarına, skalar denir. Tanım: k skalar sayısı ve a=[aij]mxn matrisi verilmiş olsun. k. A=k[aij]mxn=[kaij]mxn matrisine, k skalar sayısı ile A matrisinin çarpımı denir. Örnek: Matrisi v ek=2 saysı için, k. A matrisini bulalım. Çözüm: MATRİSLER

Tanım: A matrisi mxn türünde, B matrisi nxp türünde olsun. A. B matrisi mxp türünde bir matristir. cij, A. B nin bir elemanı ise, bu eleman, A’nın i. satır vektörü ile B’nin j. sütun vektörünün skaler çarpımına eşittir. Örnek: ve ise A. B çarpımını bulunuz. Çözüm: MATRİSLER

1. Çarpma işleminin değişme özelliği yoktur. 2. A ve B 0’a eşit olmadığı halde , A. B=0 olabilir. 3. A. 0=0. A=0’dır. Buna göre sıfır matrisi yutan elemandır. 4. Birim matris çarpma işleminin etkisiz elemanıdır. A. I=I. A=A 5. Matrislerde çarpma işleminin birleşme özelliği vardır. A. (B. C)=(A. B). C 6. Matrislerde çarpma işleminin dağılma özelliği vardır. a. Matrislerde çarpma işleminin toplama işlemi üzerine soldan dağılma özelliği; b. Matrislerde çarpma işleminin toplama işlemi üzerine sağdan dağılma özeliği; c. A ve B matrisleri mxn türünde , C matrisi nxp türünde iseler d. (A+B). C=A. C+B. C olur. 7. A ve B birer matris , k bir sayı ise ; k. (A. B)=A. (k. B)=(k. A). B dir. 8. A sıfır değilken ve A. B=A. C iken, B=C olmayabilir. MATRİSLER

Tanım: n. Sıradan bir A kare matrisi için, A. B=B. A= koşulunu sağlayan n. Sıradan B kare matrisi varsa; B matrisine , A matrisinin çarpma işlemine göre tersi denir. Çarpma İşlemine Göre Ters Matrislerin Özellikleri 1. tersi varsa, olmak üzere , n. Sıradan bir A kare matrisinin çarpma işlemine göre 2. n. Sıradan A ve B kare matrislerinin çarpma işlemine göre tersleri, 3. ise, Eğer ad-bc=0 ise, dır. yoktur. MATRİSLER ve ise;

Tanım: elde edilen matrisinin sütunları satır ya da satırları sütun haline getirmekle matrisine A matrisinin devriği denir ve veya ile gösterilir. Teorem: A ve B matrisleri mxn türünden iki matris ve k bir skalar ise; 1. 2. Teorem: ve 3. matrisleri için, Teorem: A tersi olan bir matris ise, dir. Simetrik-Antisimetrik-Ortogonal 1. =A ise, A matrisine simetrik matris denir. 2. =-A ise A matrisine antisimetrik matris denir. 3. = ise A matrisine ortogonal matris denir. MATRİSLER dir.

DETERMİNANTIN TANIMI MİNÖR VE KOFAKTÖR ÇARPIMI (EŞ ÇARPAN) DETERMİNANT FONKSİYONU DETERMİNANT ÖZELLİKLERİ EK MATRİSİN ÖZELLİKLERİ A-1 MATRİSİN EK MATRİS YARDIMIYLA BULUNUŞU

Bu kısımda, elemanları gerçek sayı olan kare matrislere ait determinant kavramını vereceğiz. A kare matris olmak üzere, A matrisinin determinantı | A| veya det(A) biçiminde gösterilir. A matrisi nxn biçiminde ise, A’nın determinantı n. mertebedendir, denir. Tanım: 1 x 1 biçimindeki matrisinin determinantı, dir. Örneğin; A=[7] matrisi için Tanım: 2 x 2 biçimindeki dir. matrisinin determinantı Tanım: 3 x 3 biçimindeki matrisinin determinantı; dir. DETERMİNANTLAR

Tanım: n. sıradan bir A kare matrisinin i. Satır ve j. Sütun atıldıktan sonra geriye kalan matrisin determinantına, elemanının Minör’ü denir ve ile gösterilir. Tanım: 3 x 3 türünden bütün matrislerin kümesi olsun. olmak üzere, fonksiyonuna, determinant fonksiyonu denir. ile tanımlı Örnek: determinantını hesaplayalım. Çözüm: 3000=a dersek, olur. Buna göre, açılımını =(a+1). (a-1)-(a-3). (a+3)=[(a. a)-1]-[(a. a)-9]=8 DETERMİNANTLAR

Tanım: n. Mertebeden kare matrislerin kümesi olsun. olmak üzere ile tanımlı fonksiyonuna, determinant fonksiyonu; D(A)= determinantı denir. Örnek: ifadesine de A matrisinin değerini bulalım. Çözüm: =-1. (-8+2+2 -6)+2. (4+1+1 -3) = -1. (-10)+2. (3)=16 bulunur. DETERMİNANTLAR

1) Bir kare matrisin, determinant değeriyle devriğinin determinant değeri eşittir. A karesel matris ise, dir. 2) Bir kare matrisin iki satır veya sütun elemanları orantılı ise, bu matrisin determinantının değeri sıfırdır. determinantı verilmiş olsun. Bu determinantın birinci satırındaki terimlerle ikinci satırındaki terimler, karşılıklı olarak orantılı olduğu için, dır. 3) Bir kare matrisin herhangi bir satır veya sütununda buluna tüm terimler sıfır ise, determinantın değeri sıfırdır. =0 dır. DETERMİNANTLAR

4) Bir kare matriste bir köşegenin üstündeki yada altındaki tüm elemanlar sıfır ise determinantın değeri köşegen üzerindeki elemanların çarpımı ya da bu çarpımın ters işaretlisine eşittir. (Asal köşegen altındaki elemanlar sıfırdır. ) 5) Bir determinantın iki satırı veya sütunu aralarında yer değiştirilirse, determinant işaret değiştirir. ise dır. (1. Satır ile 2. Satır yer değiştirmiştir. ) 6) Bir determinantın bir satır veya sütunu k sayısı ile çarpılırsa, determinantın değeri de k katına çıkar. ise olur. DETERMİNANTLAR

7) Bir determinantın herhangi bir satırında veya sütununda bulunan tüm terimlerin k katı alınarak, başka bir satırın veya sütunun elemanlarıyla toplanarak elde edilen yeni determinantın değeri değişmez. dir. (1. Satırın k katı 2. Satıra eklenmiştir. ) 8) Bir determinantın herhangi bir satırında veya sütunundaki her eleman iki terimin toplamından oluşuyorsa, bu determinant aynı sıradan iki determinantın toplamı biçiminde yazılabilir. Determinantı aynı sıradan iki determinantın toplamı biçiminde yazılırsa ; olur. DETERMİNANTLAR

9. Bir determinantın herhangi bir satır yada sütunun ait terimler, bir başka satır veya sütunun terimlerine ait eş çarpanlar ile karşılıklı çarpılır ve çarpımlar toplanırsa, toplam sıfır olur. 3. Sıradan bir determinantta a 11*A 21+a 12*A 22+a 13*A 23 = 0 dır. 10. N. Mertebeden A ve B matrisleri için, ve DETERMİNANTLAR dir.

Tanım: n. mertebeden kare matrisi verilmiş olsun. aij elemanının kofaktörü Aij ise ; matrisine, A matrisinin ek matrisi denir ve Ek(A) ile gösterilir Matrisinin ek matrisi bulunurken, tanıma göre matriste her elemanın yerine kofaktörü yazılır ve elde edilen matrisin transpozu alınır. İşaretleri değişir. Yerleri değişir. DETERMİNANTLAR

A. Ek(A)=Ek(A). A= . I Yukarıdaki özelliği, A= Matrisi için gösterelim: =(ad-bc) DETERMİNANTLAR

A-1 Matrisinin Ek Matris Yardımıyla Bulunuşu: Teorem: A matrisi olan bir matris olmak üzere, dır. İspat: A. Ek(A) = A. I eşitliğinin her iki tarafını, soldan A-1 ile çarpalım: DETERMİNANTLAR

Örnek: matrisinin tersini bulalım. Çözüm: olduğu için , det(A) yı ve Ek(A) yı bulalım. éa Sonuç : ê ëc A -1 bù ú matrisinde , det(A) = ad - bc ¹ 0 ise ; dû - bù é d Ek(A) 1 = = êú d ır. a û det(A) ad - bc ë c DETERMİNANTLAR