LEM ve MODLER ARTMETK LEM 5 3 8

İŞLEM ve MODÜLER ARİTMETİK İŞLEM : 5 + 3 = 8 olduğunu biliyoruz. Eşitliğin solunda iki sayı olduğu halde, eşitliğin sağında bir sayı vardır. Eşitliğin solundaki iki sayıyı (5, 3) ikilisi biçiminde yazalım. Şimdi bu ikiliyi 8’e eşleyen bir f fonksiyonu düşünebilirsiniz. f(5, 3) = 5+3 olur. Reel sayılar kümesinde yaptığımız, toplama, çıkarma, çarpma ve bölme işlemleri reel sayılar kümesinin kartezyen çarpımının bir alt kümesinden reel sayılar kümesine birer fonksiyondur. Tanım : Boş olmayan A, B, C kümeleri verilmiş olsun Ax. B nin bir alt kümesinden C ye tanımlı her fonksiyona işlem denir. Ax. A nın bir alt kümesinden A’ya tanımlı her fonksiyona A kümesinde bir işlem denir. İşlemi göstermek için *, +, -, � , , , . . . gibi işaretler kullanılır.

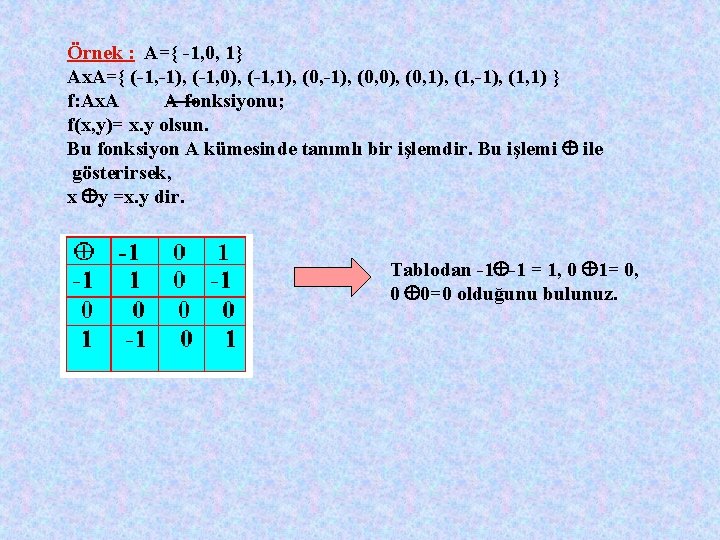
Örnek : A={ -1, 0, 1} Ax. A={ (-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 0), (0, 1), (1, -1), (1, 1) } f: Ax. A A fonksiyonu; f(x, y)= x. y olsun. Bu fonksiyon A kümesinde tanımlı bir işlemdir. Bu işlemi ile gösterirsek, x y =x. y dir. Tablodan -1 -1 = 1, 0 1= 0, 0 0=0 olduğunu bulunuz.

Örnek : Reel sayılar kümesinde , x #y =2 x-2 y+xy olmak üzere, # işlemi tanımlanıyor. a. (2 #3) #4 işleminin sonucu nedir? b. (2 #x) #2=16 eşitliğini sağlayan x değeri nedir? Çözüm : a. 2#3= 4 -3. 3 +2. 3 =1 olduğundan; ( 2 #3 ) #4= 1 #4= 2 -12+4= -6 b. 2 #x=4 -3 x+2 x=4 -x olduğundan; (2 #x) #2= (4 -x) #2 =2(4 -x)-6+( 4 -x) #2 =8 -2 x-6+8 -2 x =-4 x+10=16 -4 x=6 x=-6/4 bulunur.

İŞLEMİN ÖZELLİKLERİ : A boş olmayan bir küme ve , A’ da tanımlı bir işlem olsun; ü x, y A için x y A ise A kümesi işlemine göre kapalıdır. ü x, y A için x y= y x ise işlemin değişme özelliği vardır. ü x, y, z A için (x y) z=x (y z) ise işlemin birleşme özelliği vardır. ü x A için x e= e x=x olacak şekilde bir e A varsa e’ ye etkisiz eleman denir. ü A kümesinin işlemine göre etkisiz elemanı e olsun. x A için x x-1= x-1 x=e olacak şekilde bir x-1 A varsa x-1 ‘e x’in işlemine göre tersi denir. ü * A da tanımlı bir işlem olsun. x, y, z A için, x (y*z)= (x y)*(z x) eşitlikleri sağlanıyorsa işlemini * işlemi üzerine dağılma özelliği vardır denir.

Örnek : Z ‘ de işlemi x, y, z A için ; x y=(x+y) / 2 şeklinde tanımlanıyor. işlemine göre Z kümesi kapalımıdır. Çözüm : x, y, z A için, x x, y, z A için y Z dir. Çünkü toplamı çift olan sayıların ikiye bölümü tam sayıya karşılık gelirken, toplamı tek olan sayıların ikiye bölümü tam sayı değildir. Mesela; 2, 7 z için 2 7= (2+7) /2= 9 / 2 Z dir.

Örnek : a b c d e a e a b c b c d e d e b c c d d e e a a b KÖŞEGEN A= { a, b, c, d, e} kümesinde işlemi yukarıdaki tablo ile tanımlanıyor. v A kümesi işlemine göre kapalı mıdır? v işlemi değişme özelliğine sahip midir? v işlemine göre etkisiz eleman nedir? v b’ nin tersi nedir?

Çözüm : v işlemine göre A kümesinin herhangi iki elemanının sonucu yine A kümesinin bir elemanı olduğu için A kümesi kapalıdır. v x, y A için x y=y x olduğundan işlemi değişmelidir. v x A için x c=c x=x olduğu için c etkisiz elemandır. Gerçekten a c=a, b c=b, c c=c, d c=d, e c=e dir. v b’nin tersi olsun. b x=c olmalıdır. x=d olduğu tabloda görülür.

Örnek: x, y R için x y=x+y+2 xy işlemi tanımlanıyor. 1. 2. 3. işlemi değişmeli midir? işlemine göre etkisiz eleman nedir? işlemine göre a R olmak şartıyla a’nın tersi nedir? 4. Çözüm: ü x y= x + y+ 2 xy = y + x + 2 yx = y x O halde değişmelidir. ü Etkisiz eleman e olsun. x e = x olmalıdır. x+e+2 xe = x e+2 xe =0 e(1+2 x) =0 1+2 x 0 ise e=0 dır. Bu durumda etkisiz eleman 0’dır.

ü a’nın tersi a-1 olsun. a a-1=0 olmalıdır. a+a-1 + 2 a. a-1=0 a-1(1+2 a)=-a a-1 =-a/(1+2 a) bulunur. Örnek : © işlemi R+ da tanımlı bir işlem olmak üzere, 1/m n 2 = m. n ise 4 9 neye eşittir? Çözüm : 4 9= 1/ (1/4) 32 =1/4. 3 = 3/4‘ tür.

Örnek : R 2 de tanımlanan (a, b) (c, d) =( a+c, b+d) işleminin etkisiz elemanı nedir? Çözüm : Etkisiz eleman (x. Y) olsun. İşlem değişme özelliğine sahip olduğu için; (a, b) (x, y)=(a, b) olmalıdır. (a+x, b+y)= (a, b) ise a+x=a ve b+x= b x=0 , y=0 bulunur. Demek ki etkisiz eleman (0, 0) ‘dır.

MODÜLER ARİTMETİK : Z ‘ de ={ x, y} : m (x-y)}, m 1 ve m Z+ bağıntısı denklik bağıntısıdır. O halde (x , y) için x y (mod m) Örnek : Z de ={ x, y : 5 (x-y)} denklik bağıntısını inceleyelim. Çözüm : , farklı 5’e bölünen tamsayı ikililerinden oluşmaktadır. Yani (1, 6), (74, 69). . . denklik bağıntısı olduğu için x(x, y) için x y (mod 5) Mesela; (1, 6) olduğu için 1 6 (mod 5) (74, 69) olduğu için 74 69 (mod 5). . .

Z’ de m=5 modülüne göre ‘nın denklik sınıflarını ( kalan sınıfları) oluşturalım. 0={. . . , -10 , -5, 0, 5, 10, . . . } 1={. . . , -9 , -4, 1, 6, 11, . . . } 2={. . . , -8 , -3 , 2, 7, 12. . . } 3={. . . , -7, -2 , 3, 8, 13, . . . } 4={. . . , -6 , -1, 4, 9, 14, . . . } 5 modülüne göre kalan sınıflarıdır. Z/m={ 0, 1 , 2, 3. . . (m-1)} dir. ÖZELLİKLER : x y ( mod m) ve u= v olsun. Ø x ve y nin ( u ve y in ) m’ ye bölümünden kalan eşittir. Ø x-y , (u-v) m 2 ye tam olarak bölünür.

Ø x+ u y+v (mod m) Ø x-u y-v (mod m) Ø x. u y. v ( mod m) Ø c. x c. y (mod m) , c Z Ø xn y-n ( mod m ) , n Z+ Z/m ‘ de Toplama ve Çıkarma : x , y Z/m için 1. x +y = x+y 2. x. y = x. y

Örnek : Z/5 de 4. ( 2+ 4) +3 işleminin sonucu nedir? Çözüm : 4. ( 2+ 4) +3 =4. ( 2+ 4)+ 3 =4. 6+ 3 =4. 1+ 3 =4+3 =7 = 2

Örnek : 71962 x ( mod 11) ise x nedir? Çözüm : 710= 1 dir. Buna göre , 71964 (710)196. 72 11196. 72 5 MATEMATİK SİSTEMLER (mod 11) : Tanım: A boş olmayan bir küme olmak şartıyla A ‘ da tanımlı bir işlem olsun. ( A, ) ikilisine bir matematik sistem denir. * ‘ da A ‘ da tanımlı bir işlem ise ( A, , *) üçlüsüne de bir matematik sistem denir.

Tanım : G, boş olmayan bir küme olmak şartıyla A da tanımlı bir işlem olsun. (G, ) sistemi aşağıdaki özellikleri sağlıyorsa grup adını alır. • Kapalılık özelliği; • Birleşme özelliği; • Etkisiz eleman özelliği ; • Ters eleman özelliği ; Tanım : (G, ) grubu değişme özelliği sağlıyorsa değişmeli grup adını alır. Örneğin (Z, +), (R, . ), (Z/5, +) sistemleri birer değişmeli gruptur fakat ( N, +), (Z, . ) (Z/4, . ) sistemleri birer değişmeli grup değildir.

Tanım : (H, , &) matematik sistemi aşağıdaki şartları sağlıyorsa halka adını alır. 1. 2. 3. 4. (H, ) değişmeli gruptur. H kümesi & işlemine göre kapalıdır. & işlemine göre birleşme özelliği vardır. & işleminin işlemi üzerine dağılma özelliği vardır. Tanım : (H, , &) halka olmak şartıyla; 1. & işlemi değişme özelliğine sahipse, (H, , &) değişmeli halka adını alır. 2. & işleminde etkisiz eleman özelliği varsa (H, , &) birimli halka adını alır.

Örnek : (Z, +, . ) değişmeli ve birimli halkadır. Tanım : (C, , &) matematik sistemi aşağıdaki şartları sağlıyorsa, bir cisim adını alır. 1. 2. 3. (C, ) sistemi değişmeli grup ve birim elemanı e’ dir. (C-{e}, &) sistemi değişmeli gruptur. & işleminin işlemi üzerine dağılma özelliği vardır. Tanım : ( C, , &) bir cisim olsun. & işleminin değişme özelliği varsa ( C, , &) Sistemi değişmeli cisim adını alır.