Mathematical Induction Copyright Cengage Learning All rights reserved

















































































- Slides: 86

Mathematical Induction Copyright © Cengage Learning. All rights reserved.

Mathematical Induction is a method for proving that: a property defined for integers n is true for all values of n that are greater than or equal to some initial integer.

Mathematical Induction is a method for proving that: a property defined for integers n is true for all values of n that are greater than or equal to some initial integer.

Example If we get rid of pennies (1 cent) and replace with new coins of 3 cents value, With only 3 -cent coins and 5 -cent coins, can we still give changes of n cents for any positive integer n>7? n=8: 8 = 3+5 n=9: 9 = 3+3+3 n=10: 10=5+5 n=11: 11=3+3+5 n=12: 12=3+3+3+3 n=13: … How do you convince/prove for any n>7?

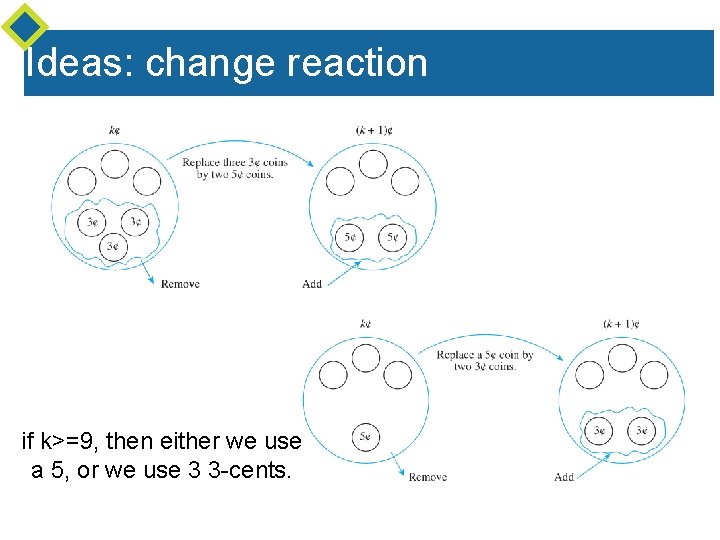
Ideas With only 3 -cent coins and 5 -cent coins, can we still give changes of n cents for any positive integer n>7? If we can give changes of k cents, how to create solution to (k+1) cents from it? n=8: 8 = 3+5 n=9: 9 = 3+3+3 n=10: 10=5+5 n=11: 11=3+3+5 n=12: 12=3+3+3+3 n=13: … any pattern?

Ideas: change reaction if k>=9, then either we use a 5, or we use 3 3 -cents.

Ideas: change reaction • We can give change of 9 cents. • for any k>=9, if we can give change of k cents, then we can give change of k+1 cents. * So we can give change of 10 cents. * why? * So we can give change of 11 cents. * why? * Continue forever…

Logic behind: change reaction • We can give change of 9 cents. p(9) • for any k>=9, if we can give change of k cents, then we can give change of k+1 cents. for any k>=9, if P(k) then P(k+1) * So we can give change of 10 cents. * Universal Modus Ponens * So we can give change of 11 cents. * Universal Modus Ponens * Continue forever…

Mathematical Induction: two steps

Example 1 – Sum of the First n Integers Use mathematical induction to prove that Solution: first identify property P(n). Here, P(n) i: [To see that P(n) is a sentence, its subject being “the sum of the integers from 1 to n” and its verb is “equals. ”]

Example 1 – Solution Basis step: show that the property is true for n = 1, i. e. , P(1) is true. P(1) is obtained by substituting 1 in place of n in P(n). The left-hand side of P(1) is the sum of all the successive integers starting at 1 and ending at 1. This is just 1. Thus P(1) is cont’d

Example 1 – Solution this equation is true because the right-hand side is which equals the left-hand side. cont’d

Example 1 – Solution cont’d Inductive step: assume that P(k) is true, for a particular but arbitrarily chosen integer k with k ≥ 1. You must then show that P(k + 1) is true. What are P(k) and P(k + 1)? P(k) is obtained by substituting k for every n in P(n). Thus P(k) is Thus P(k + 1) is or, equivalently,

Example 1 – Solution In this case, left-hand side of P(k + 1) is 1 + 2 +· · ·+ (k + 1), which equals (1 + 2 +· · ·+ k) + (k + 1) But by substitution from the inductive hypothesis, cont’d

Example 1 – Solution cont’d

Example 1 – Solution So the left-hand side of P(k + 1) is cont’d . Now the right-hand side of P(k + 1) is Thus the two sides of P(k + 1) are equal to each other, and so the equation P(k + 1) is true.

Applying the Formula for the Sum of the First n Integers a. Evaluate 2 + 4 + 6 +· · ·+ 500. b. Evaluate 5 + 6 + 7 + 8 +· · ·+ 50. c. For an integer h ≥ 2, write 1 + 2 + 3 +· · ·+ (h – 1) in closed form.

Mathematical Induction Geometric sequence: each term is obtained from the preceding one by multiplying by a constant factor. for example: 1, r, r 2, r 3, . . . , r n, . . sum of first n terms of this sequence is given by the formula for all integers n ≥ 0 and real numbers r not equal to 1.

Mathematical Induction in expanded form: and because r 0 = 1 and r 1 = r, the formula for n ≥ 1 can be rewritten as

Sum of a Geometric Sequence Prove that , for all integers n ≥ 0 and all real numbers r except 1. Solution: In this example property P(n) is again an equation, although in this case it contains a real variable r :

Example 3 – Solution Because r can be any real number other than 1, the proof begins by supposing that r is a particular but arbitrarily chosen real number not equal to 1. Then the proof continues by mathematical induction on n, starting with n = 0. In the basis step, you must show that P(0) is true; that is, you show the property is true for n = 0. cont’d

Example 3 – Solution cont’d So you substitute 0 for each n in P(n): Is P(0) true? In inductive step, you suppose k is any integer with k ≥ 0 for which P(k) is true; that is, you suppose the property is true for n = k.

Example 3 – Solution So you substitute k for each n in P(n): Then you show that P(k + 1) is true; that is, you show the property is true for n = k + 1. So you substitute k + 1 for each n in P(n): cont’d

Example 3 – Solution Or, equivalently, In inductive step, we use another common technique for showing that an equation is true: We start with the left-hand side, transform it step-by-step into the right-hand side, using the inductive hypothesis together with algebra and other known facts. cont’d

Example 3 – Solution cont’d Proof (by mathematical induction): Suppose r is a particular but arbitrarily chosen real number that is not equal to 1, and let the property P(n) be the equation We must show that P(n) is true for all integers n ≥ 0. We do this by mathematical induction on n.

Example 3 – Solution cont’d Show that P(0) is true: To establish P(0), we must show that The left-hand side of this equation is r 0 = 1 and the hand side is also because r 1 = r and r ≠ 1. Hence P(0) is true. right-

Example 3 – Solution cont’d Show that for all integers k ≥ 0, if P(k) is true then P(k + 1) is also true: [Suppose that P(k) is true for a particular but arbitrarily chosen integer k ≥ 0. That is: ] Let k be any integer with k ≥ 0, and suppose that [We must show that P(k + 1) is true. That is: ] We must show that

Example 3 – Solution Or, equivalently, that [We will show that the left-hand side of P(k + 1) equals the right-hand side. ] The left-hand side of P(k + 1) is cont’d

Example 3 – Solution cont’d which is the right-hand side of P(k + 1) [as was to be shown. ] [Since we have proved the basis step and the inductive step, we conclude that theorem is true. ]

Proving an Equality

Proving an Equality Two different ways to show that an equation is true: 1. transforming the LHS (left-hand side) and RHS (righthand side) independently until they are seen to be equal, and 2. transforming one side of the equation until it is the same as the other side of the equation. 3. another approach: show LHS >= RHS, and RHS>=LHS, and then they have to equal to each other

Proving an Equality Sometimes people use a method that they believe proves equality but that is actually invalid. e. g. , to prove basis step for Theorem 5. 2. 3: What’s going on here? The problem with this method is that starting from a statement and deducing a true conclusion does not prove that the statement is true.

Proving an Equality A true conclusion can also be deduced from a false statement. For instance, the steps below show to deduce the true conclusion that 1 = 1 from the false statement that 1 = 0:

Alternative way to prove Let Then and so

Deducing Additional Formulas But Equating the right-hand sides of equations (5. 2. 1) and (5. 2. 2) and dividing by r – 1 gives This derivation of the formula is attractive and is quite convincing. However, it is not as logically airtight as the proof by mathematical induction.

Proving a Divisibility Property Use mathematical induction to prove that for all integers n ≥ 0, 22 n – 1 is divisible by 3. Solution: What is P(n)? I P(n) is the sentence

Example 1 – Solution By substitution, the statement for the basis step, P(0), is The supposition for the inductive step, P(k), is and the conclusion to be shown, P(k + 1), is cont’d

Example 1 – Solution cont’d We know that an integer m is divisible by 3 if, and only if, m = 3 r for some integer r. Now the statement P(0) is true because 22 ● 0 – 1 = 20 – 1 = 1 – 1 = 0, which is divisible by 3 because 0 = 3 ● 0. To prove the inductive step, you suppose that k is any integer greater than or equal to 0 such that P(k) is true. This means that 22 k – 1 is divisible by 3. You must then prove the truth of P(k + 1). Or, in other words, you must show that 22(k+1) – 1 is divisible by 3.

Example 1 – Solution cont’d But The aim is to show that this quantity, 22 k ● 4 – 1, is divisible by 3. Why should that be so? By the inductive hypothesis, 22 k – 1 is divisible by 3, and 22 k ● 4 – 1 resembles 22 k – 1.

Example 1 – Solution Observe what happens, if you subtract 22 k – 1 from ● 4 – 1: cont’d 22 k Adding 22 k – 1 to both sides gives Both terms of the sum on the right-hand side of this equation are divisible by 3; hence the sum is divisible by 3.

Example 1 – Solution cont’d Therefore, the left-hand side of the equation is also divisible by 3, which is what was to be shown. This discussion is summarized as follows: Proof (by mathematical induction): Let the property P(n) be the sentence “ 22 n – 1 is divisible by 3. ”

Example 1 – Solution Show that P(0) is true: To establish P(0), we must show that But and 0 is divisible by 3 because 0 = 3 ● 0. Hence P(0) is true. cont’d

Example 1 – Solution Show that for all integers k ≥ 0, if P(k) is true then P(k + 1) is also true: [Suppose that P(k) is true for a particular but arbitrarily chosen integer k ≥ 0. That is: ] Let k be any integer with k ≥ 0, and suppose that By definition of divisibility, this means that cont’d

Example 1 – Solution cont’d [We must show that P(k + 1) is true. That is: ] We must show that But

Example 1 – Solution cont’d But is an integer because it is a sum of products of integers, and so, by definition of divisibility, is divisible by 3 [as was to be shown]. [Since we have proved the basis step and the inductive step, we conclude that the proposition is true. ]

Example 2 – Proving an Inequality Use mathematical induction to prove that for all integers n ≥ 3, Solution: In this example the property P(n) is the inequality By substitution, the statement for the basis step, P(3), is

Example 2 – Solution cont’d The supposition for the inductive step, P(k), is and the conclusion to be shown is To prove the basis step, observe that the statement P(3) is true because 2 ● 3 + 1 = 7, 23 = 8, and 7 < 8.

Example 2 – Solution To prove the inductive step, suppose the inductive hypothesis, that P(k) is true for an integer k ≥ 3. This means that 2 k + 1 < 2 k is assumed to be true for a particular but arbitrarily chosen integer k ≥ 3. Then derive the truth of P(k + 1). Or, in other words, show that the inequality is true. But by multiplying out and regrouping, and by substitution from the inductive hypothesis, cont’d

Example 2 – Solution cont’d Hence If it can be shown that 2 k + 2 is less than 2 k+1, then the desired inequality will have been proved. But since the quantity 2 k can be added to or subtracted from an inequality without changing its direction, And since multiplying or dividing an inequality by 2 does not change its direction,

Example 2 – Solution cont’d This last inequality is clearly true for all k ≥ 2. Hence it is true that. This discussion is made more flowing (but less intuitive) in the following formal proof: Proof (by mathematical induction): Let the property P(n) be the inequality

Example 2 – Solution Show that P(3) is true: To establish P(3), we must show that But Hence P(3) is true. cont’d

Example 2 – Solution cont’d Show that for all integers k ≥ 3, if P(k) is true then P(k + 1) is also true: [Suppose that P(k) is true for a particular but arbitrarily chosen integer k ≥ 3. That is: ] Suppose that k is any integer with k ≥ 3 such that [We must show that P(k + 1) is true. That is: ] We must show that

Example 2 – Solution cont’d Or, equivalently, But [This is what we needed to show. ] [Since we have proved the basis step and the inductive step, we conclude that the proposition is true. ]

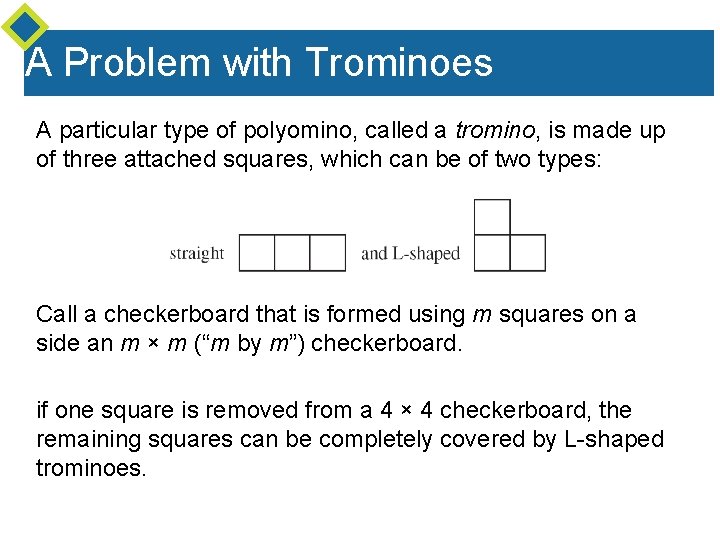
A Problem with Trominoes

A Problem with Trominoes A particular type of polyomino, called a tromino, is made up of three attached squares, which can be of two types: Call a checkerboard that is formed using m squares on a side an m × m (“m by m”) checkerboard. if one square is removed from a 4 × 4 checkerboard, the remaining squares can be completely covered by L-shaped trominoes.

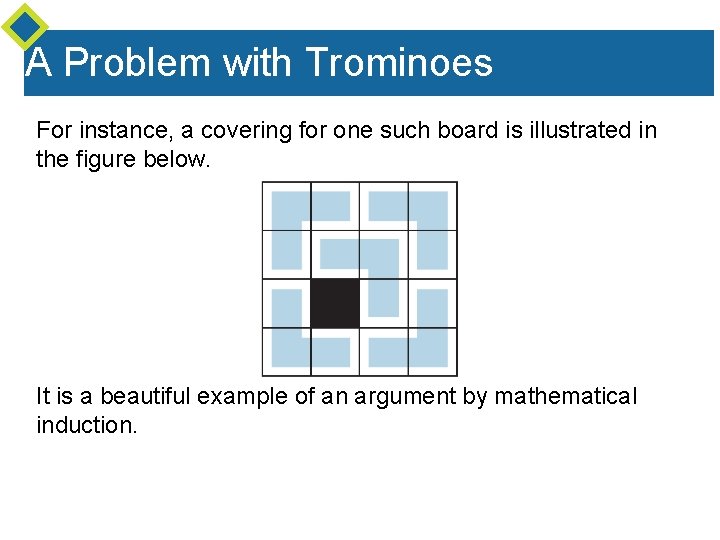
A Problem with Trominoes For instance, a covering for one such board is illustrated in the figure below. It is a beautiful example of an argument by mathematical induction.

A Problem with Trominoes The main insight leading to a proof of this theorem is the observation that because , when a board is split in half both vertically and horizontally, each half side will have length 2 k and so each resulting quadrant will be a checkerboard.

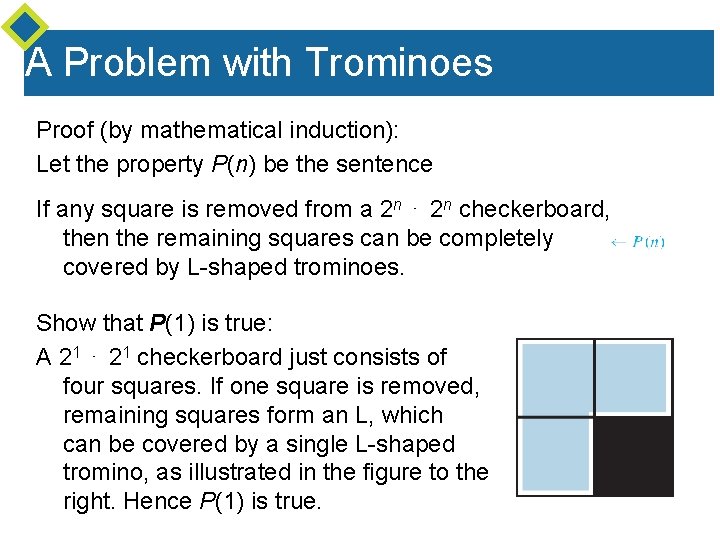
A Problem with Trominoes Proof (by mathematical induction): Let the property P(n) be the sentence If any square is removed from a 2 n ⋅ 2 n checkerboard, then the remaining squares can be completely covered by L-shaped trominoes. Show that P(1) is true: A 21 ⋅ 21 checkerboard just consists of four squares. If one square is removed, remaining squares form an L, which can be covered by a single L-shaped tromino, as illustrated in the figure to the right. Hence P(1) is true.

A Problem with Trominoes Show that for all integers k ≥ 1, if P(k) is true then P(k + 1) is also true: [Suppose that P(k) is true for a particular but arbitrarily chosen integer k ≥ 3. That is: ] Let k be any integer such that k ≥ 1, and suppose that If any square is removed from a 2 k ⋅ 2 k checkerboard, then the remaining squares can be completely covered by L-shaped trominoes.

A Problem with Trominoes P(k) is the inductive hypothesis. [We must show that P(k + 1) is true. That is: ] We must show that If any square is removed from a 2 k+1 ⋅ 2 k+1 checkerboard, then the remaining squares can be completely covered by L-shaped trominoes.

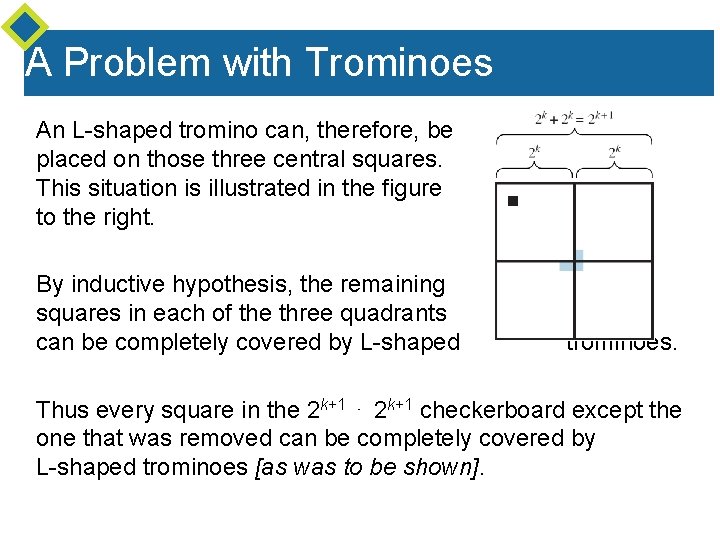
A Problem with Trominoes Consider a 2 k+1 ⋅ 2 k+1 checkerboard with one square removed. Divide it into four equal quadrants: Each will consist of a 2 k × 2 k checkerboard. In one of the quadrants, one square will have been removed, and so, by inductive hypothesis, all the remaining squares in this quadrant can be completely covered by L-shaped trominoes. The other three quadrants meet at the center of the checkerboard, and the center of the checkerboard serves as a corner of a square from each of those quadrants.

A Problem with Trominoes An L-shaped tromino can, therefore, be placed on those three central squares. This situation is illustrated in the figure to the right. By inductive hypothesis, the remaining squares in each of the three quadrants can be completely covered by L-shaped trominoes. Thus every square in the 2 k+1 ⋅ 2 k+1 checkerboard except the one that was removed can be completely covered by L-shaped trominoes [as was to be shown].

Strong Mathematical Induction and the Well-Ordering Principle for the Integers Copyright © Cengage Learning. All rights reserved.

Strong Mathematical Induction similar to ordinary mathematical induction • a technique for proving of a sequence of statements about integers. • also consists of a basis step and an inductive step. Difference • basis step may contain proofs for several initial values, • inductive step: prove: for any integer k>=a, if P(a), P(a+1) … P(k), then P(k + 1)

Strong Mathematical Induction also known as second principle of induction, second principle of finite induction, and principle of complete induction.

Strong Mathematical Induction Any statement that can be proved with ordinary math. induction can be proved with strong math. induction. given any integer k ≥ b, if the truth of P(k) alone implies the truth of P(k + 1), then certainly the truth of P(a), P(a + 1), . . . , and P(k) implies the truth of P(k + 1).

Strong Mathematical Induction Any statement that can be proved with strong math. induction can be proved with ordinary math. induction. Strong Math. Induction Ord. Math Induction Let Q(n)= • P(a), P(a+1), … P(b) * Q(b) • for any k>=b, if P(a), P(a+1), … P(k) are true, then P(k+1) is true * for any k>=b, if Q(k) then Q(k+1)

Applying Strong Mathematical Induction

Example 1 – Divisibility by a Prime Prove: Any integer greater than 1 is divisible by a prime number. Solution: inductive step? If a given integer greater than 1 is not itself prime, then it is a product of two smaller positive integers, each of which is greater than 1. I Since you are assuming that each of these smaller integers is divisible by a prime number, by transitivity of divisibility, those prime numbers also divide the integer you started with.

Example 1 – Solution Proof (by strong mathematical induction): Let the property P(n) be the sentence n is divisible by a prime number. Show that P(2) is true: To establish P(2), we must show that 2 is divisible by a prime number. this is true because 2 is divisible by 2 and 2 is a prime number. cont’d

Example 1 – Inductive step cont’d Show that for all integers k ≥ 2, if P(i ) is true for all integers i from 2 through k, then P(k + 1) is also true: Let k be any integer with k ≥ 2 and suppose that i is divisible by a prime number for all integers i from 2 through k. We must show that k + 1 is divisible by a prime number.

Example 1 – Solution cont’d Case 1 (k + 1 is prime): k + 1 is divisible by a prime number, namely itself. Case 2 (k + 1 is not prime): k + 1 = ab where a and b are integers with 1 < a < k + 1 and 1 < b < k + 1. as 2 ≤ a ≤ k, and so by inductive hypothesis, a is divisible by a prime number p. In addition because k + 1 = ab, we have that k + 1 is divisible by a.

Example 1 – Solution cont’d a| (k + 1) and p| a , so by transitivity of divisibility, p| (k + 1) Therefore, regardless of whether k + 1 is prime or not, it is divisible by a prime number [as was to be shown]. [Since we have proved both the basis and the inductive step of the strong mathematical induction, we conclude that the given statement is true. ]

Well-Ordering Principle for the Integers

Well-Ordering Principle for the Integers • Well-ordering principle for integers • ordinary principles of mathematical induction, • strong principles of mathematical induction but it can be shown that all three principles are equivalent, i. e. , if any one of the three is true, then so are both of the others.

Well-Ordering Principle for the Integers Prove that any integer greater than 1 is divisible by a prime number. Proof: Suppose not, i. e. , there exist some integers greater than 1 that is not divisible by a prime. Let C be the set of all integers greater than one that is not divisible by any primes, so C is not empty. By well-ordering principle, there exists a least element in C, call it n. n cannot be prime (as if it’s prime, then n|n, and n is not in C) so n = ab, where 1<a, b<n, therefore a, b are not in C so a and b are divisible by some prime numbers p, q, by transitivity of divisibility, p|n, then n is not in C.

Well-Ordering Principle for the Integers Prove that any integer greater than 1 is divisible by a prime number. Proof: Suppose not, i. e. , there exist some integers greater than 1 that is not divisible by a prime. Let C be the set of all integers greater than one that is not divisible by any primes, so C is not empty. By well-ordering principle, there exists a least element in C, call it n. [we will derive a contradiction]

Finding Least Elements Does the set has a least element? If so, what is it? If not, explain why the well-ordering principle is not violated. a. the set of all positive real numbers.

Finding Least Elements In each case, if the set has a least element, state what it is. If not, explain why the well-ordering principle is not violated. b. the set of all nonnegative integers n such that n 2 < n.

Example 4 – Solution cont’d b. There is no least nonnegative integer n such that n 2 < n because there is no nonnegative integer that satisfies this inequality. The well-ordering principle is not violated because the well -ordering principle refers only to sets that contain at least one element.

Finding Least Elements In each case, if the set has a least element, state what it is. If not, explain why the well-ordering principle is not violated. c. The set of all nonnegative integers of the form 46 – 7 k, where k is an integer. { 46 -7 k | k is an integer} 46 is an element…

Well-Ordering Principle for the Integers by subtracting six 7’s from 46 leaves 4 left over This is the least nonnegative integer obtained by repeated subtraction of 7’s from 46. • 6 is the quotient and • 4 is the remainder for the division of 46 by 7. More generally, in the division of any integer n by any positive integer d, the remainder r is the least nonnegative integer of the form n – dk.

Well-Ordering Principle for the Integers Proof: Let S be the set of all nonnegative integers of the form where k is an integer.

The Well-Ordering Principle for the Integers This set has at least one element. [For if n is nonnegative, then and so n – 0 ● d is in S. And if n is negative, then and so n – nd is in S. ] By well-ordering principle, S contains a least element r. Then, for some specific integer k = q, [because every integer in S can be written in this form].

The Well-Ordering Principle for the Integers Adding dq to both sides gives Furthermore, r < d. [For suppose r ≥ d. Then and so n – d(q + 1) would be a nonnegative integer in S that would be smaller than r. But r is the smallest integer in S. This contradiction shows that the supposition r ≥ d must be false. ]

Well-Ordering Principle for the Integers The preceding arguments prove that there exist integers r and q for which [This is what was to be shown. ]
 Copyright 2015 all rights reserved
Copyright 2015 all rights reserved Copyright 2015 all rights reserved
Copyright 2015 all rights reserved Dell all rights reserved copyright 2009
Dell all rights reserved copyright 2009 Copyright © 2018 all rights reserved
Copyright © 2018 all rights reserved Copyright cengage learning. powered by cognero
Copyright cengage learning. powered by cognero Specification by example
Specification by example All rights reserved sentence
All rights reserved sentence Freesound content licence
Freesound content licence Confidential all rights reserved
Confidential all rights reserved Sentinel-controlled loop pseudocode
Sentinel-controlled loop pseudocode Pearson education inc all rights reserved
Pearson education inc all rights reserved Microsoft corporation. all rights reserved.
Microsoft corporation. all rights reserved. Microsoft corporation. all rights reserved.
Microsoft corporation. all rights reserved. Microsoft corporation. all rights reserved.
Microsoft corporation. all rights reserved. Pearson education inc. all rights reserved
Pearson education inc. all rights reserved Warning all rights reserved
Warning all rights reserved Siprop
Siprop Quadratic equation cengage
Quadratic equation cengage Warning all rights reserved
Warning all rights reserved Confidential all rights reserved
Confidential all rights reserved Microsoft corporation. all rights reserved
Microsoft corporation. all rights reserved 2010 pearson education inc
2010 pearson education inc 2017 all rights reserved
2017 all rights reserved Copyright 2010 pearson education inc
Copyright 2010 pearson education inc 2010 pearson education inc
2010 pearson education inc Confidential all rights reserved
Confidential all rights reserved Confidential all rights reserved
Confidential all rights reserved R rights reserved
R rights reserved Rights reserved
Rights reserved Strong induction
Strong induction Eecs 203
Eecs 203 Mathematical induction divisibility
Mathematical induction divisibility Geometric series proof by induction
Geometric series proof by induction Mathematical induction
Mathematical induction Proof by mathematical induction
Proof by mathematical induction Mathematical induction
Mathematical induction How to prove by induction
How to prove by induction Geometric sequence closed form
Geometric sequence closed form Principle of mathematical induction
Principle of mathematical induction Proof by induction
Proof by induction Mathematical vs non mathematical economics
Mathematical vs non mathematical economics Chapter 6:2 interpreting word parts
Chapter 6:2 interpreting word parts Chapter 5 learning exercises medical terminology
Chapter 5 learning exercises medical terminology Cengage learning heart diagram
Cengage learning heart diagram South-western cengage learning
South-western cengage learning Chapter 13 medical math assignment sheet cengage learning
Chapter 13 medical math assignment sheet cengage learning 2009 delmar cengage learning
2009 delmar cengage learning Cengage learning heart diagram
Cengage learning heart diagram Chapter 1 matching medical terminology
Chapter 1 matching medical terminology Cengage learning australia
Cengage learning australia Graphing tpr
Graphing tpr Whille
Whille Cengage learning
Cengage learning Wadsworth cengage learning
Wadsworth cengage learning Cengage learning
Cengage learning Cengage learning plant cell
Cengage learning plant cell Cengage learning
Cengage learning Cengage learning
Cengage learning Brooks cole cengage learning
Brooks cole cengage learning Cengage learning chapter 7 answers
Cengage learning chapter 7 answers 2014 cengage learning accounting answers
2014 cengage learning accounting answers Cengage learning
Cengage learning Cengage learning
Cengage learning Chapter 6 skeletal system
Chapter 6 skeletal system Cengage learning
Cengage learning 2009 delmar cengage learning
2009 delmar cengage learning Consumer behavior cengage
Consumer behavior cengage 2012 cengage learning
2012 cengage learning Training evaluation
Training evaluation Cengage learning psychology
Cengage learning psychology Course technology cengage learning
Course technology cengage learning Course technology cengage learning
Course technology cengage learning Course technology cengage learning
Course technology cengage learning Course technology cengage learning
Course technology cengage learning 2016 cengage learning
2016 cengage learning Delmar cengage learning instructor resources
Delmar cengage learning instructor resources 2014 cengage learning
2014 cengage learning 2010 cengage learning
2010 cengage learning Positive vs negative rights
Positive vs negative rights Riparian rights
Riparian rights Characteristics of rights
Characteristics of rights Legal rights vs moral rights
Legal rights vs moral rights What are negative rights
What are negative rights Negative rights
Negative rights Positive vs negative rights
Positive vs negative rights Negative right
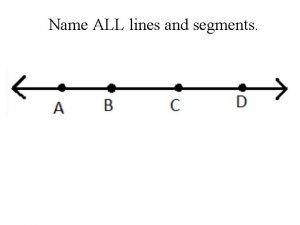
Negative right Name three line segments
Name three line segments