Mathematical Induction Induction is the most important proof

Mathematical Induction. • Induction is the most important proof method in computer science. • Suppose you want to prove that the proposition P (n) is true for all n N, where N = {0, 1, 2, …} (an infinite set). ( i. e. every natural number n has some property P) • You might be able to prove it for 0, 1, 2, … But you can’t check one-by-one that all natural numbers have property P.

• The key idea of mathematical induction is start with 0 and repeatedly add 1. • Suppose you can show that i) 0 has property P and ii) whenever you add 1 to a number that has property P the resulting number also has property P. This guarantees that as you go through the list of all natural numbers, every number you encounter must have property P.

• The proof method of mathematical induction says that you just need to do two things: i) prove it for n = 0 (basis case) ii) prove “if it’s true for n=k, then it’s true for n =k+1” Induction Hypothesis • fix some k 0 • assume P (k) Induction Step • Using assumption P (k) prove that P (k+1) In this way we prove that for any n [P(n) P(n+1)]

Why does this prove it for all n N ? Actually it relies upon the property of integers N={0, 1, 2, …} The pattern is: To prove n 0 (P (n)) it’s enough to show: 1) (Base) P (0) 2) n 0 (P(n) P (n +1)) How can we prove n 0 (P(n) P (n +1)) ? Pick arbitrary k 0 and prove it for n = k. So, in the second step we say: “take some k 0 and assume that property P holds for n = k“ (Induction Hypothesis). Then, (based upon this assumption) we need to show that the property P can be implied for n = k +1.

There is a variant if you want to prove it for n n 0 : To prove n n 0 (P (n)) it’s enough to show: 1) (Base) P ( n 0) 2) n n 0 (P(n) P (n +1)) 1) In the base case we explicitly check n = n 0 2) Pick arbitrary k n 0 and assume that the property P holds for n = k. (Induction Hypothesis) Based upon this assumption prove that the property P can be implied for n = k +1. (Induction Step)

Example. Prove that for all n 1 n! 2 n 1. Proof by induction on n 1. 1). Basis: n =1. 1!=1=21 1=20. So, for the case n=1, we checked that n! 2 n 1. 2). Assume that for n=k, k is some integer k 1, inequality holds, i. e. k! 2 k 1 (IH). We want to prove that n! 2 n 1 for n = k +1, i. e. we want to show that (k+1)! 2(k+1) 1 Using the definition of factorial we have (k+1)!= (k+1) k! (k+1) 2 k 1 ……by IH (1+1) 2 k 1 ……because k 1 = 2 2 k 1 = 2 k……QED, because 2(k+1) 1= 2 k By Induction Principle we conclude that n! 2 n 1 for all n 1

Induction proof for the summation formula Let’s prove the formula for the sum of integers from 1 to n: n 0 P (n) Alternative notation for the LHS: Thus we want to prove: n 0

Let’s stop for a moment and check that the formula we are to prove makes sense: n 0 Consider a few particular cases: • n =1 • n=0

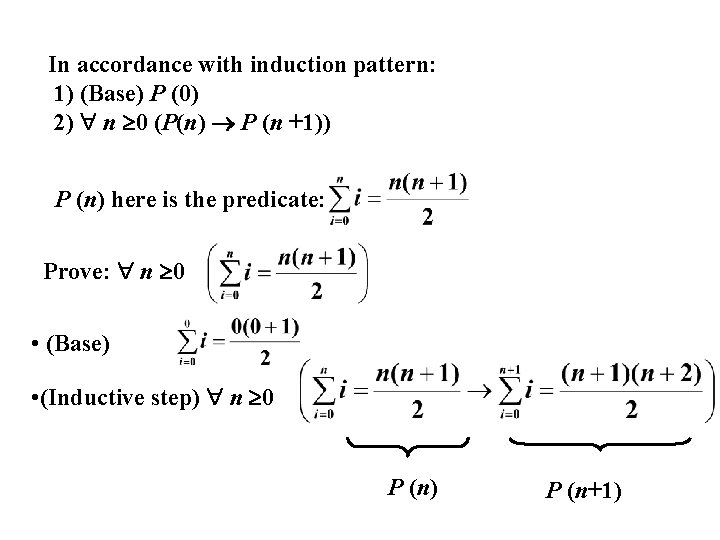
In accordance with induction pattern: 1) (Base) P (0) 2) n 0 (P(n) P (n +1)) P (n) here is the predicate: Prove: n 0 • (Base) • (Inductive step) n 0 P (n) P (n+1)

1) Basis: check that the formula is correct for the case of no terms 2) fix some k 0 and assume that proposition holds for n = k P(n=k) (induction hypothesis, IH) Show that the P(n=k+1): can be implied (IS) ……. . by IH …. algebra

Why induction proofs work? Intuitively, because we can reach any number n if we start with the smallest one and add 1 step-by-step. So, induction principle express this obvious fact. More formally, induction principle is formulated in terms of a set A = {n N | P (n)} Induction Principle. If A is a subset of N that satisfies two properties: 1) 0 A 2) n 0 [n A (n+1) A], then A =N