Chapter 14 Deductive Geometry Using Triangle Congruence and

Chapter 14 Deductive Geometry Using Triangle Congruence and Similarity

Review: Parallel Lines and Angles Definition Two different given lines L 1 and L 2 on a plane are said to be parallel if they will never intersect each other no matter how far they are extended. Definition Two angles are called vertical angles if they are opposite to each other and are formed by a pair of intersecting lines. A Theorem Any pair of vertical angles are always congruent. B

Parallel Lines and Angles Definition Given two line L 1 and L 2 (not necessarily parallel) on the plane, a third line T is called a transversal of L 1 and L 2 if it intersects these two lines. L 1 L 2 T

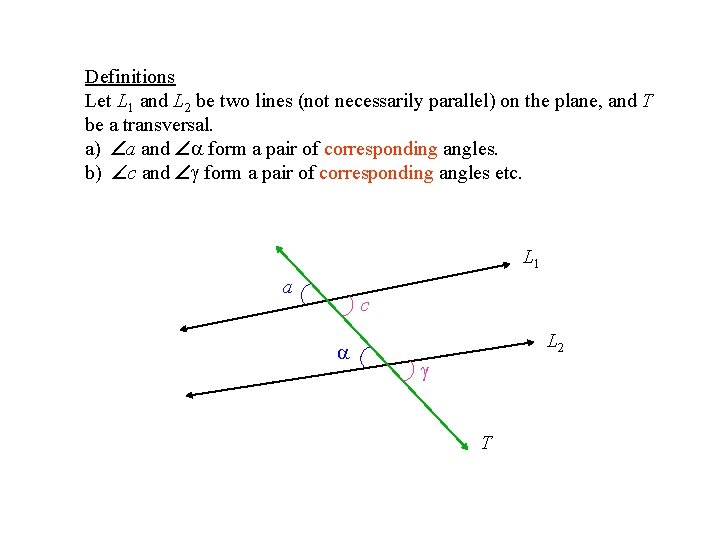
Definitions Let L 1 and L 2 be two lines (not necessarily parallel) on the plane, and T be a transversal. a) a and form a pair of corresponding angles. b) c and form a pair of corresponding angles etc. L 1 a c L 2 T

Definitions Let L 1 and L 2 be two lines (not necessarily parallel) on the plane, and T be a transversal. c) c and form a pair of alternate interior angles. d) d and form a pair of alternate interior angles. L 1 c d L 2 T

Definitions Let L 1 and L 2 be two lines (not necessarily parallel) on the plane, and T be a transversal. e) a and form a pair of alternate exterior angles. f) b and form a pair of alternate exterior angles. L 1 a L 2 T

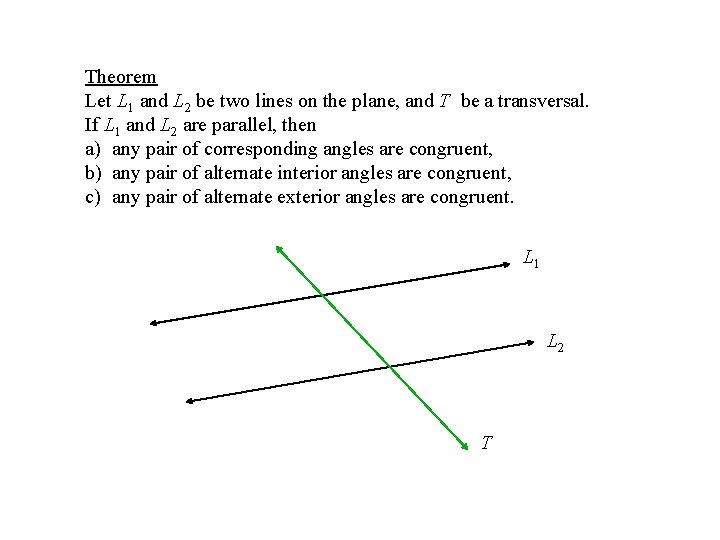
Theorem Let L 1 and L 2 be two lines on the plane, and T be a transversal. If L 1 and L 2 are parallel, then a) any pair of corresponding angles are congruent, b) any pair of alternate interior angles are congruent, c) any pair of alternate exterior angles are congruent. L 1 L 2 T

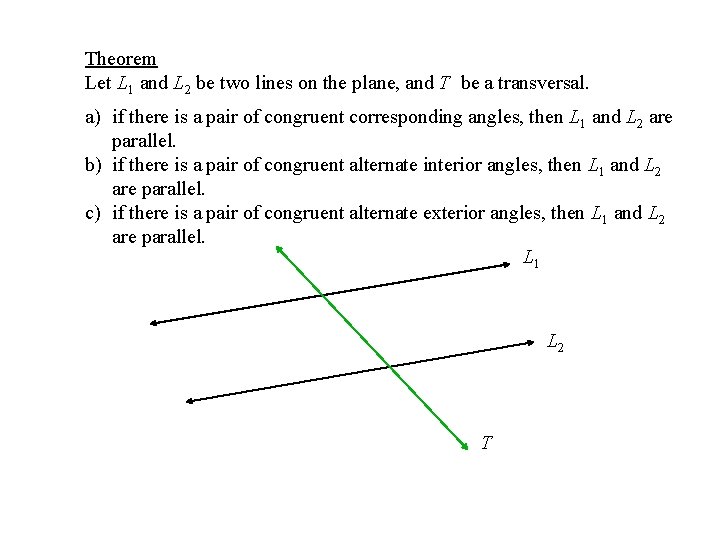
Theorem Let L 1 and L 2 be two lines on the plane, and T be a transversal. a) if there is a pair of congruent corresponding angles, then L 1 and L 2 are parallel. b) if there is a pair of congruent alternate interior angles, then L 1 and L 2 are parallel. c) if there is a pair of congruent alternate exterior angles, then L 1 and L 2 are parallel. L 1 L 2 T

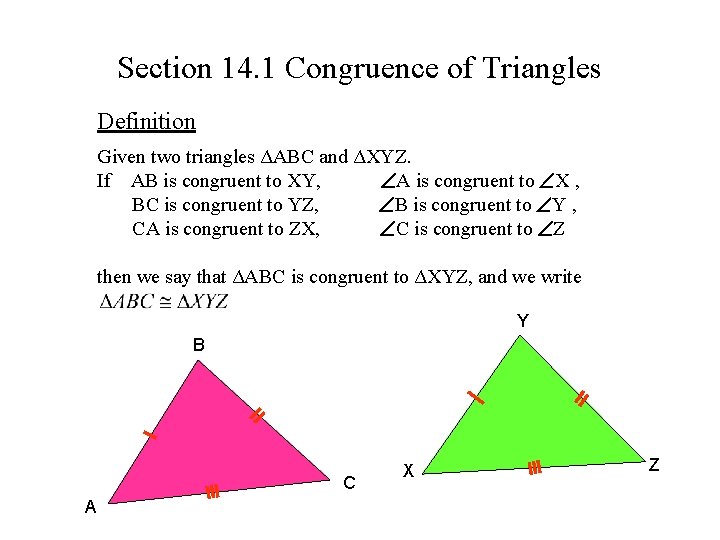
Section 14. 1 Congruence of Triangles Definition Given two triangles ΔABC and ΔXYZ. If AB is congruent to XY, A is congruent to X , BC is congruent to YZ, B is congruent to Y , CA is congruent to ZX, C is congruent to Z then we say that ΔABC is congruent to ΔXYZ, and we write Y B C A X Z

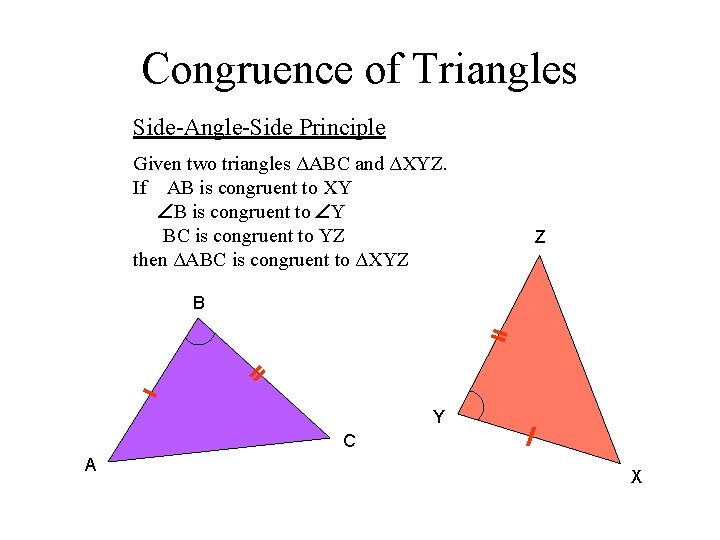
Congruence of Triangles Side-Angle-Side Principle Given two triangles ΔABC and ΔXYZ. If AB is congruent to XY B is congruent to Y BC is congruent to YZ then ΔABC is congruent to ΔXYZ Z B Y C A X

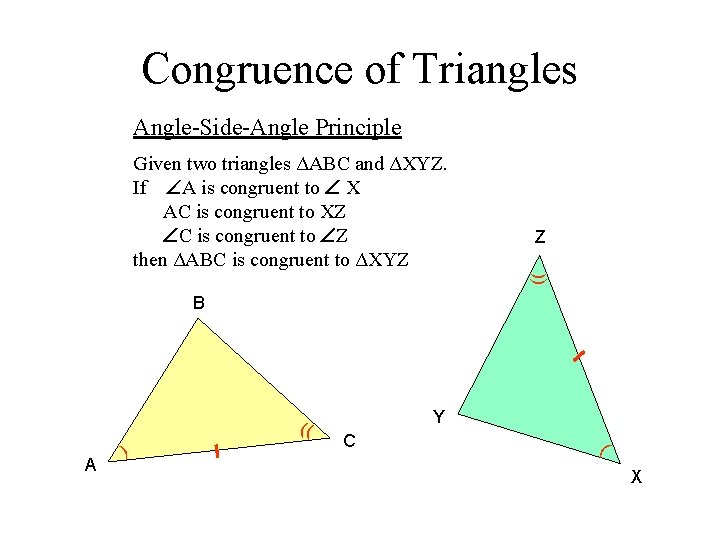
Congruence of Triangles Angle-Side-Angle Principle Z (( Given two triangles ΔABC and ΔXYZ. If A is congruent to X AC is congruent to XZ C is congruent to Z then ΔABC is congruent to ΔXYZ B (( A ) Y C ( X

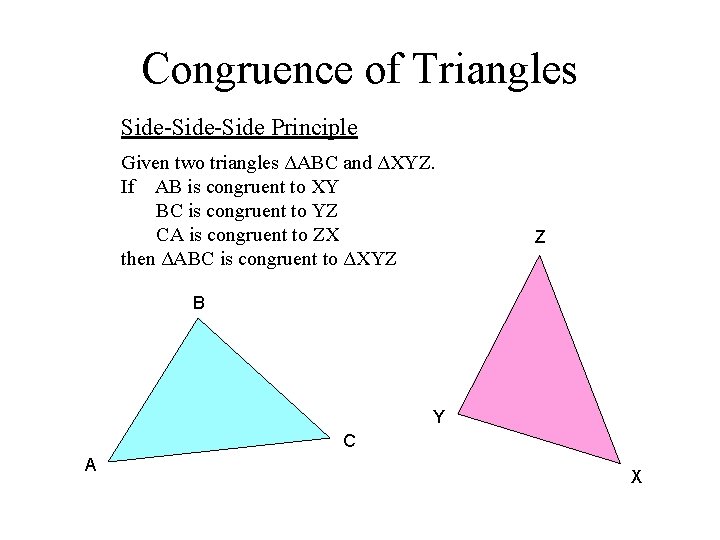
Congruence of Triangles Side-Side Principle Given two triangles ΔABC and ΔXYZ. If AB is congruent to XY BC is congruent to YZ CA is congruent to ZX then ΔABC is congruent to ΔXYZ Z B Y C A X

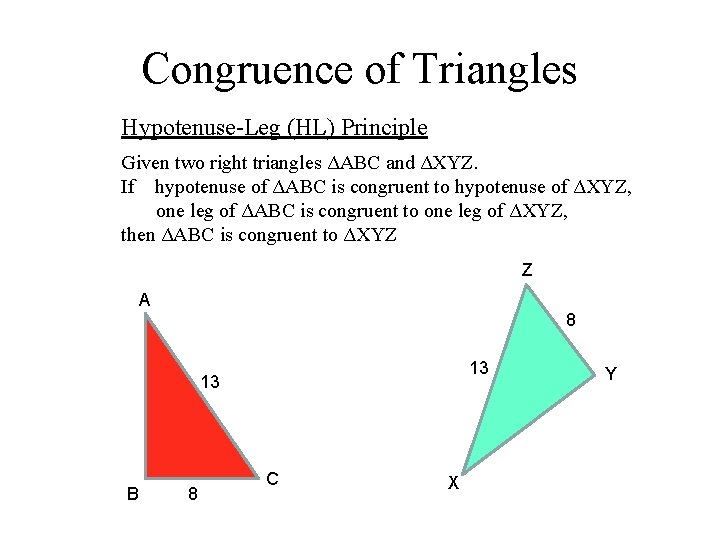
Congruence of Triangles Hypotenuse-Leg (HL) Principle Given two right triangles ΔABC and ΔXYZ. If hypotenuse of ΔABC is congruent to hypotenuse of ΔXYZ, one leg of ΔABC is congruent to one leg of ΔXYZ, then ΔABC is congruent to ΔXYZ Z A 8 13 13 B 8 C X Y

Theorem If ΔABC is congruent to ΔXYZ , then AB is congruent to XY BC is congruent to YZ CA is congruent to ZX and A is congruent to X B is congruent to Y C is congruent to Z In short, corresponding parts of congruent triangles are congruent. This is sometimes referred to as the “CPCTC” property.

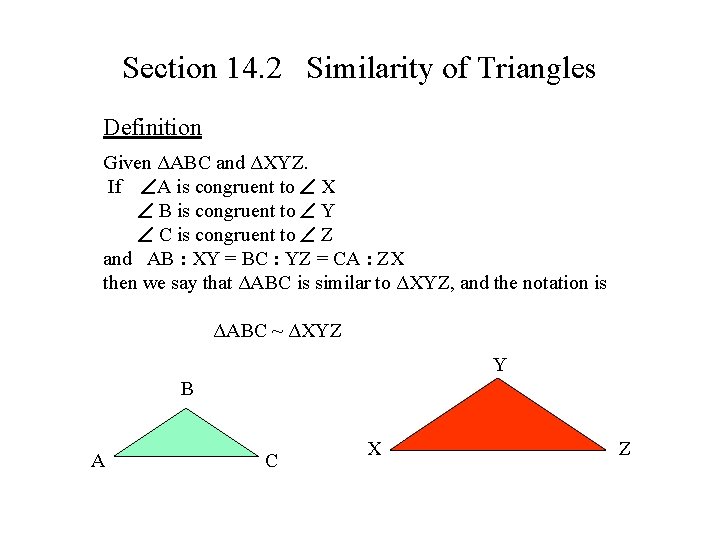
Section 14. 2 Similarity of Triangles Definition Given ΔABC and ΔXYZ. If A is congruent to X B is congruent to Y C is congruent to Z and AB : XY = BC : YZ = CA : ZX then we say that ΔABC is similar to ΔXYZ, and the notation is ΔABC ~ ΔXYZ Y B A C X Z

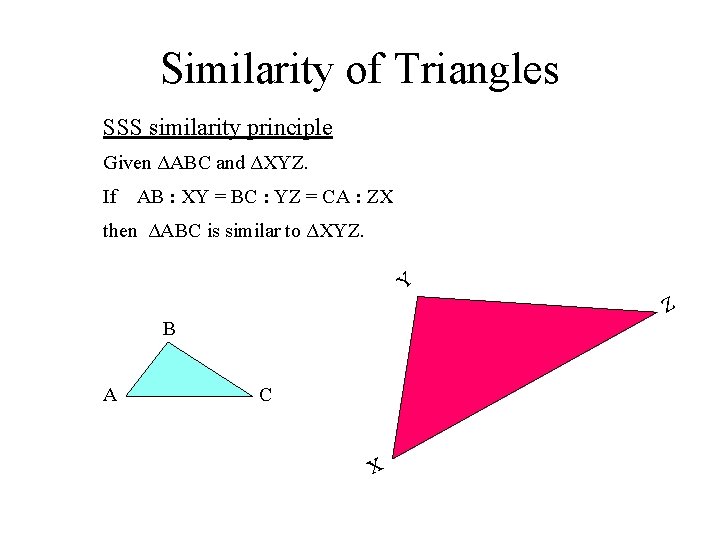
Similarity of Triangles SSS similarity principle Given ΔABC and ΔXYZ. If AB : XY = BC : YZ = CA : ZX then ΔABC is similar to ΔXYZ. Y Z B A C X

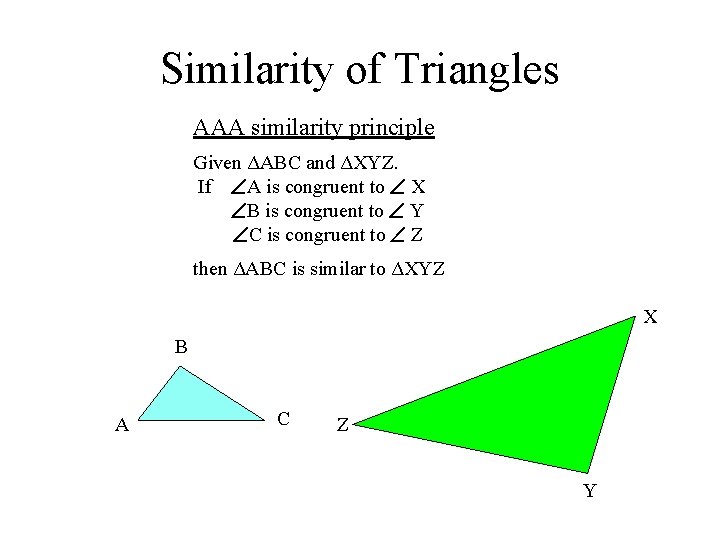
Similarity of Triangles AAA similarity principle Given ΔABC and ΔXYZ. If A is congruent to X B is congruent to Y C is congruent to Z then ΔABC is similar to ΔXYZ X B A C Z Y

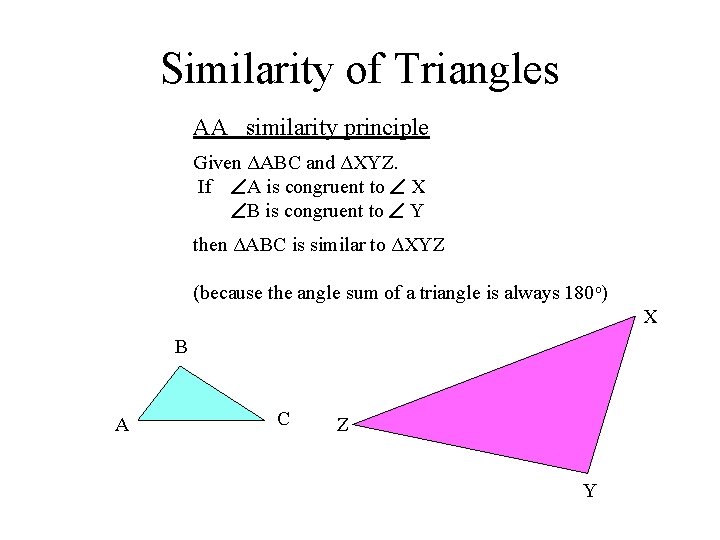
Similarity of Triangles AA similarity principle Given ΔABC and ΔXYZ. If A is congruent to X B is congruent to Y then ΔABC is similar to ΔXYZ (because the angle sum of a triangle is always 180 o) X B A C Z Y

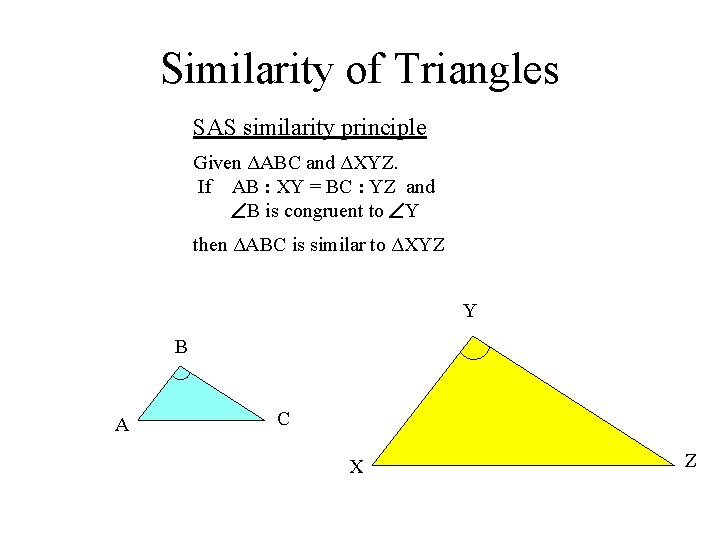
Similarity of Triangles SAS similarity principle Given ΔABC and ΔXYZ. If AB : XY = BC : YZ and B is congruent to Y then ΔABC is similar to ΔXYZ Y B A C X Z

Indirect Measurements If the shadow of a tree is 37. 5 m long, and the shadow of a 1. 5 m student is 2. 5 m long. How tall is the tree? (assuming that they are all on level ground. )

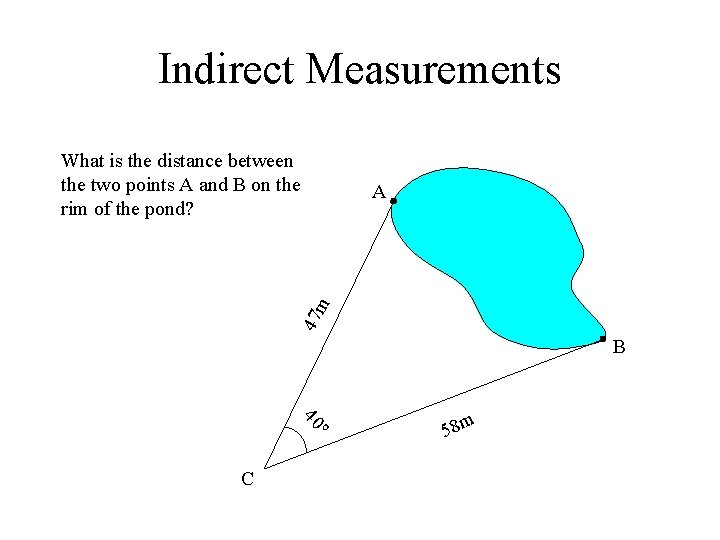
Indirect Measurements What is the distance between the two points A and B on the rim of the pond? 47 m A B o 40 C 58 m

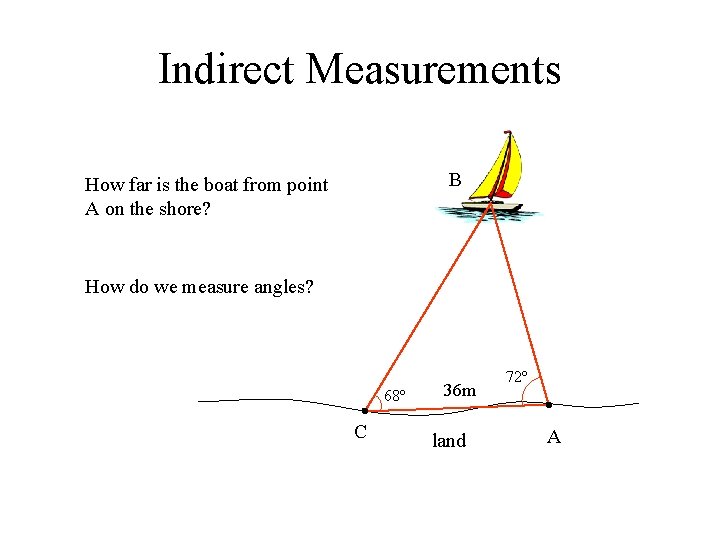
Indirect Measurements B How far is the boat from point A on the shore? How do we measure angles? 68º C 36 m land 72º A

Artillery Rangefinder

A large (3. 5 m) optical rangefinder mounted on the flying bridge of the USS Stewart (a Destroyer Escort)

A Transit is a surveying instrument to measure horizontal angles. Glass reticle on both models has stadia lines for measuring distance. Stadia ratio 1: 100

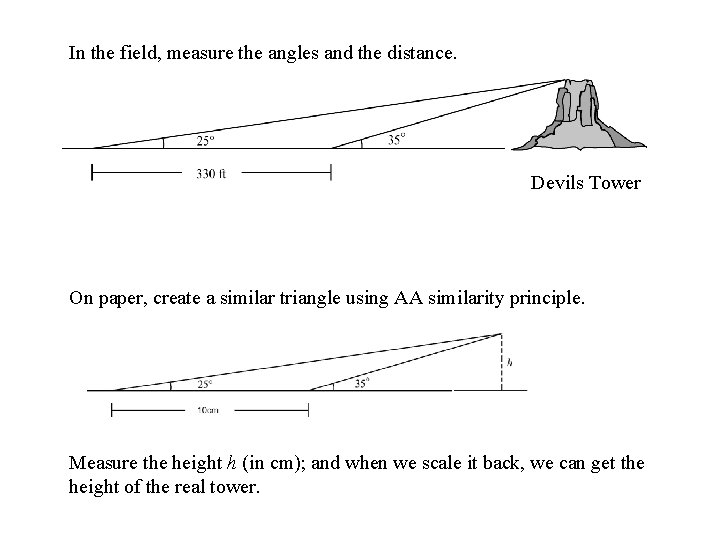
Measure the height of Devils Tower in Wyoming

In the field, measure the angles and the distance. Devils Tower On paper, create a similar triangle using AA similarity principle. Measure the height h (in cm); and when we scale it back, we can get the height of the real tower.

The first 'proper' ascent was in 1937 when some of America's best climbers took on the project. The Weissner Route was the result, a 5. 7 (decent VS) classic on which he placed a single per runner on the crux pitch.

A bizarre incident took place only a couple of years later, in 1941 when local air ace Charles George Hopkins decided to parachute onto the top of the tower to advertise his aerial show. He came prepared with a length of rope, a block and tackle as well as a sharpened axle from a Model T Ford to act as an anchor for his planned escape. His parachute descent went OK but on arrival he found that his rope had disappeared over the edge and he was well and truly stuck! There was only one solution, the first ascensionists were called upon to drive halfway across America to repeat their great feat and bring down the hapless Hopkins who had spent a cold and lonely week on his island in the sky.

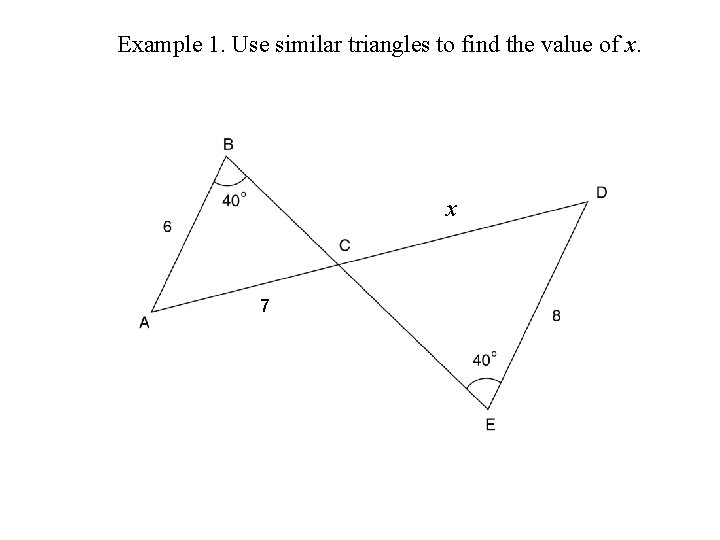
Example 1. Use similar triangles to find the value of x. x 7

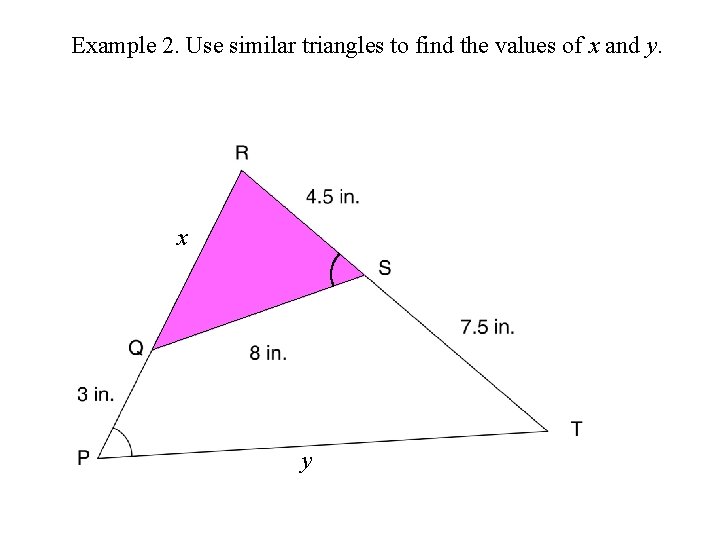
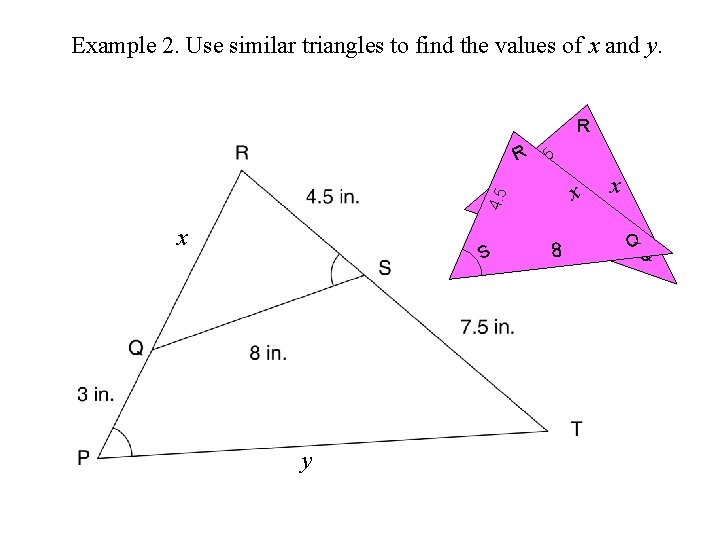
Example 2. Use similar triangles to find the values of x and y. x y

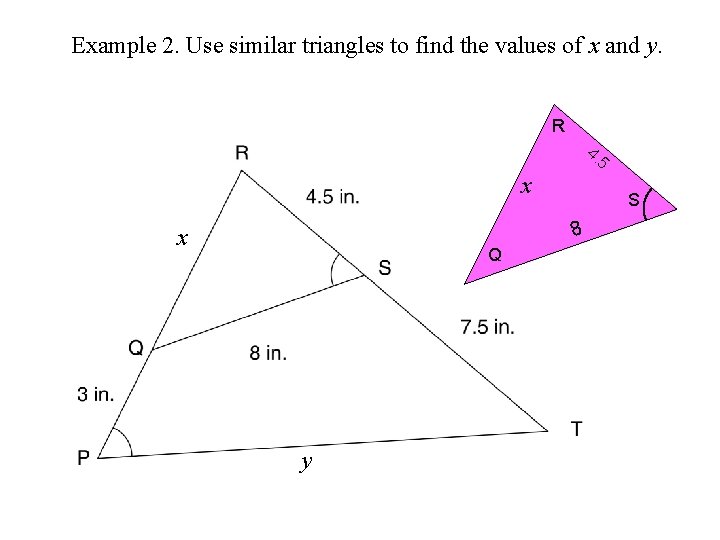
Example 2. Use similar triangles to find the values of x and y. R 4. 5 x S 8 x Q y

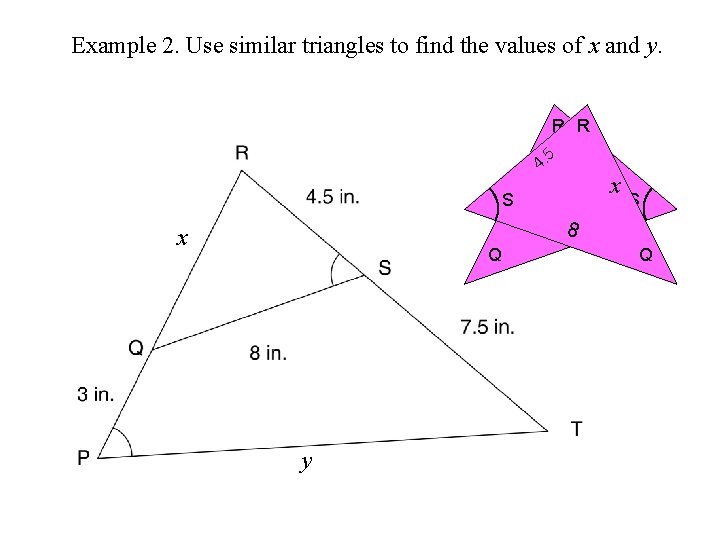
Example 2. Use similar triangles to find the values of x and y. R R S x 4. 5 x S 88 x Q y Q

Example 2. Use similar triangles to find the values of x and y. R R. 5 4 x 4. 5 S 8 x S y 8 x Q Q

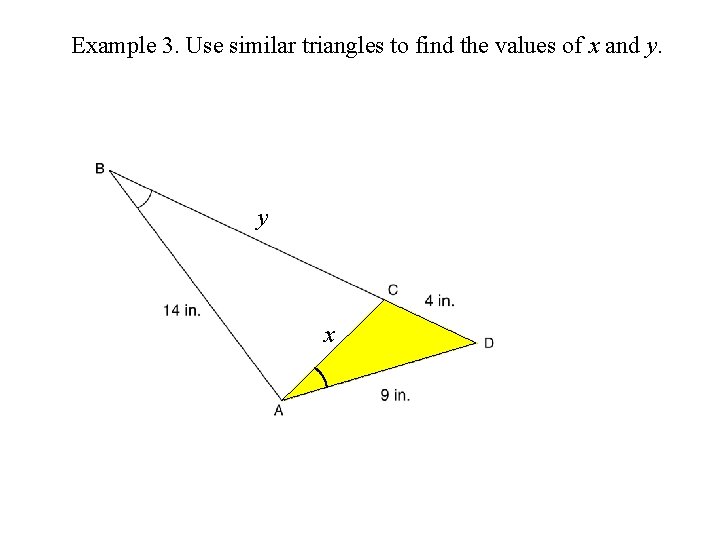
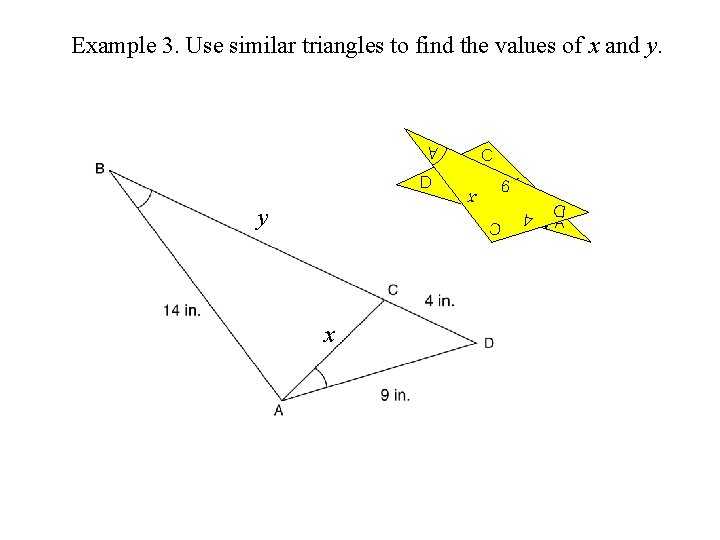
Example 3. Use similar triangles to find the values of x and y. y x

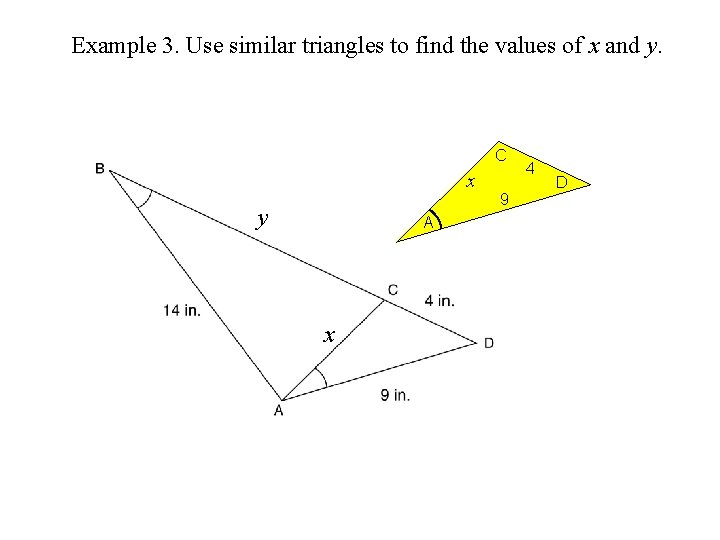
Example 3. Use similar triangles to find the values of x and y. C x y A x 9 4 D

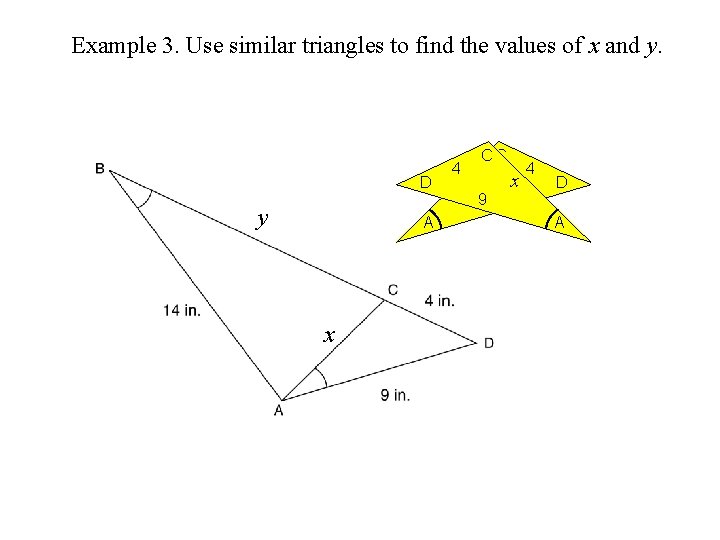
Example 3. Use similar triangles to find the values of x and y. D y A x 4 CC x 9 9 x 4 D A

Example 3. Use similar triangles to find the values of x and y. 4 x C x x D y 9 9 A D C 4 A

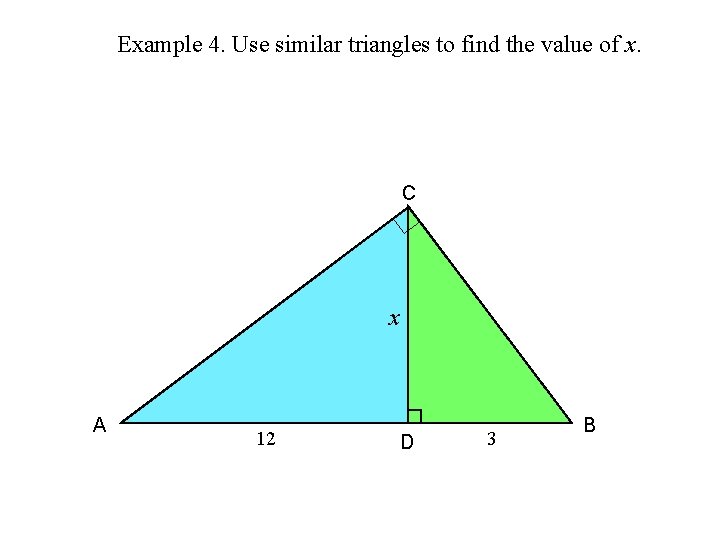
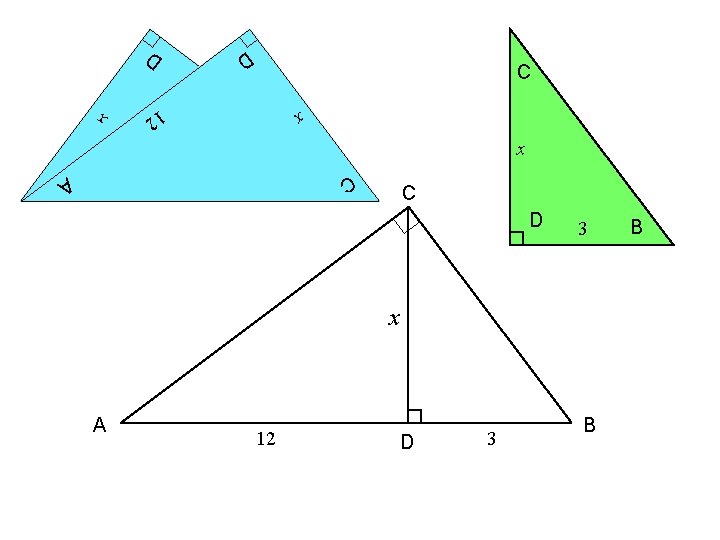
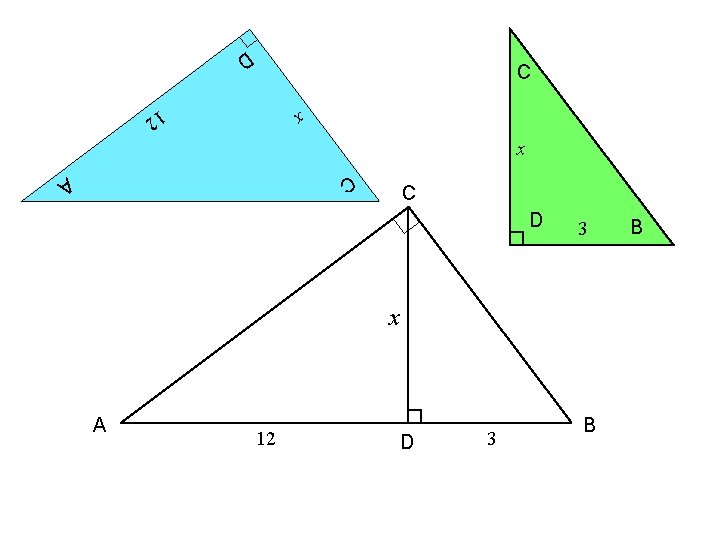
Example 4. Use similar triangles to find the value of x. C x A 12 D 3 B

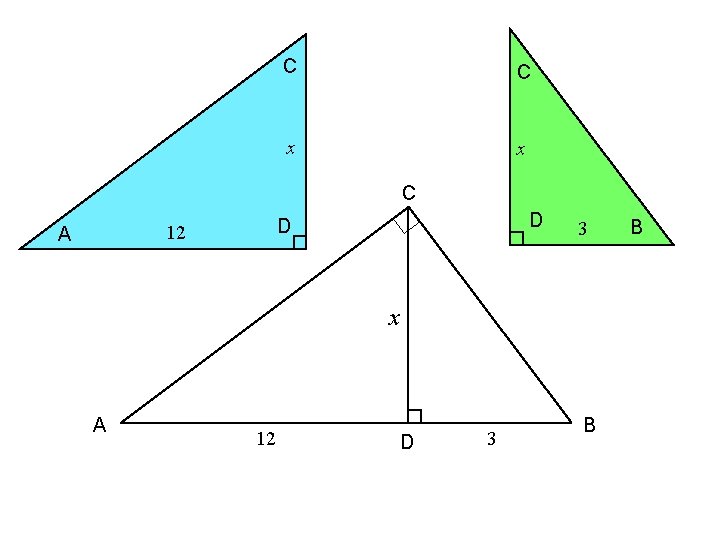
C C x x C A D D 12 3 x A 12 D 3 B B

C C x x C A D D 12 3 x A 12 D 3 B B

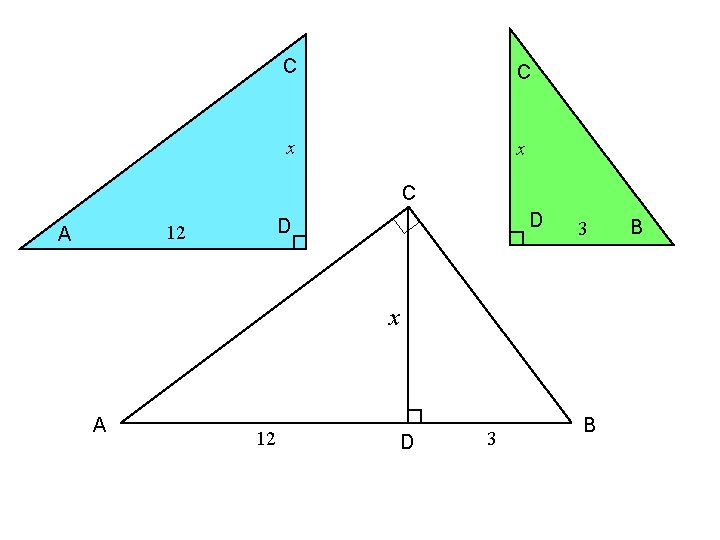
D C x x 12 D 12 x CA C AC D 3 x A 12 D 3 B B

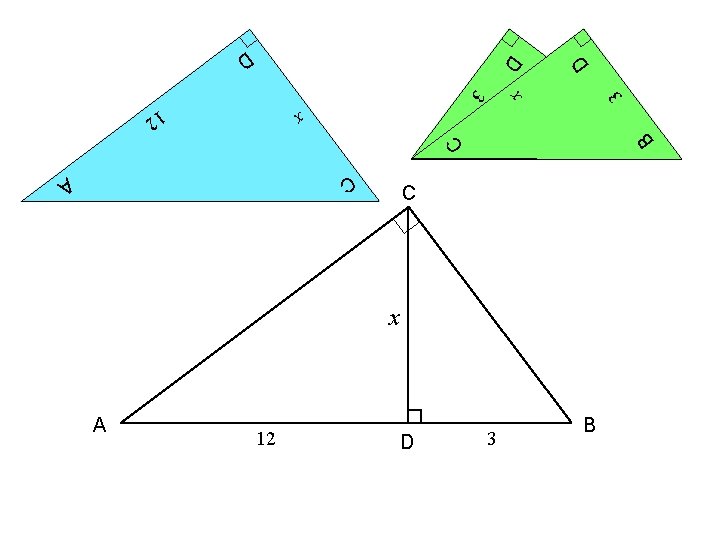
D C 12 x x C C A D 3 x A 12 D 3 B B

D x x D 12 x B C C C A x A 3 D 3 B C 12 D 3 B

Section 14. 3 Basic Euclidean Constructions (with Straight Edge and Compass) Remark A straight edge is only used to draw line segments, and it should not have any marking on it. If a ruler is used, then all the markings should be ignored.

Reasons for not using a Protractor or Ruler 1. We need to prepare for situations where some equipments are not available. 2. Small protractors are not accurate enough for large scale projects. 3. Many geometric constructions cannot be done by protractors but can be done by a compass and straight edge, such as finding the center of a circle.

What can the equipments do? 1. A straight edge is infinitely long and is only used to draw line segments connecting given points or extend an existing line segment. 2. A compass can be used to draw circles and circular arcs with radii that have already been constructed.

Basic Rules Any construction should consist of only a finite number of steps. Only one step can be carried out at a time. Each construction must be exact. Approximation is not counted as a solution. In particular, a construction should not require drawing a line tangent to an existing circular arc because that will not provide accurate results. A point must either be given in advance, or be constructed by the intersection of two line segments, or two arcs, or an arc and a line segment.

Basic Rules All compass and straightedge constructions consist of repeated application of five basic constructions using the points, lines and circles that have already been constructed or given. These are: 1. Creating the line through two existing points 2. Creating the circle through one point with centre at another point. 3. Creating the point which is the intersection of two existing, non- parallel lines. 4. Creating the one or two points in the intersection of a line and a circle. 5. Creating the one or two points in the intersection of two circles.

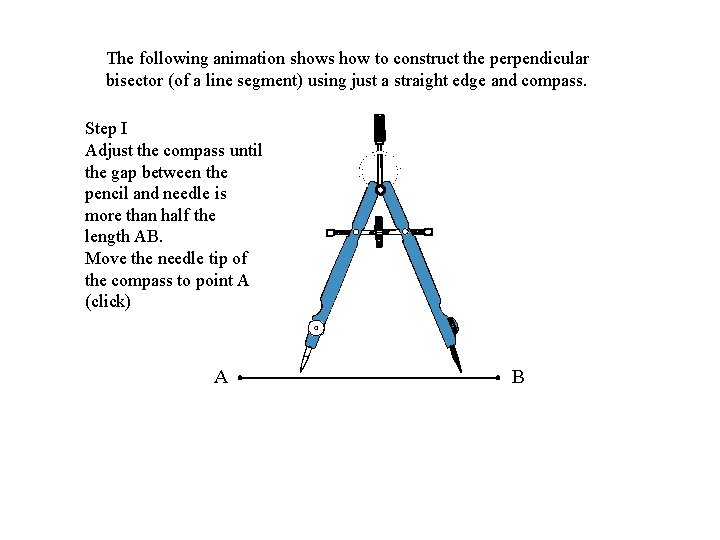
The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step I Adjust the compass until the gap between the pencil and needle is more than half the length AB. Move the needle tip of the compass to point A (click) A B

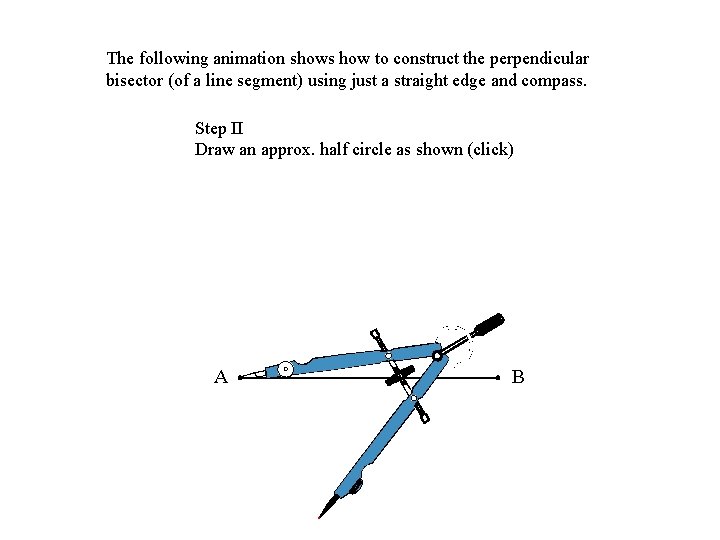
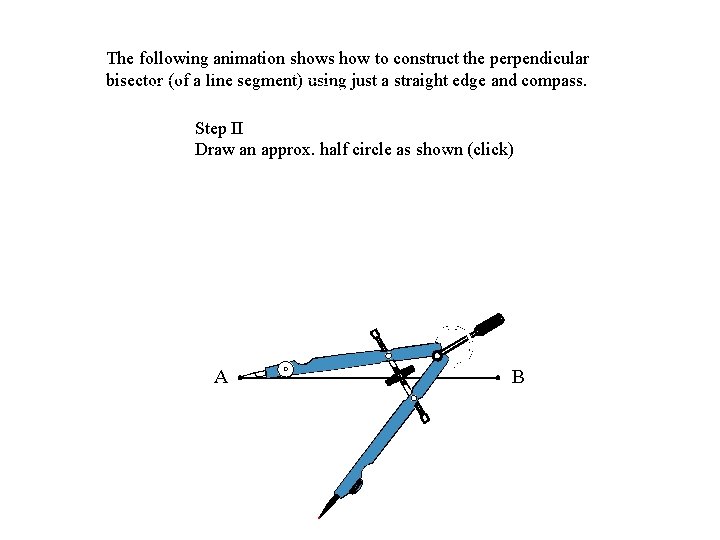
The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step II Draw an approx. half circle as shown (click) A B

The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step II Draw an approx. half circle as shown (click) A B

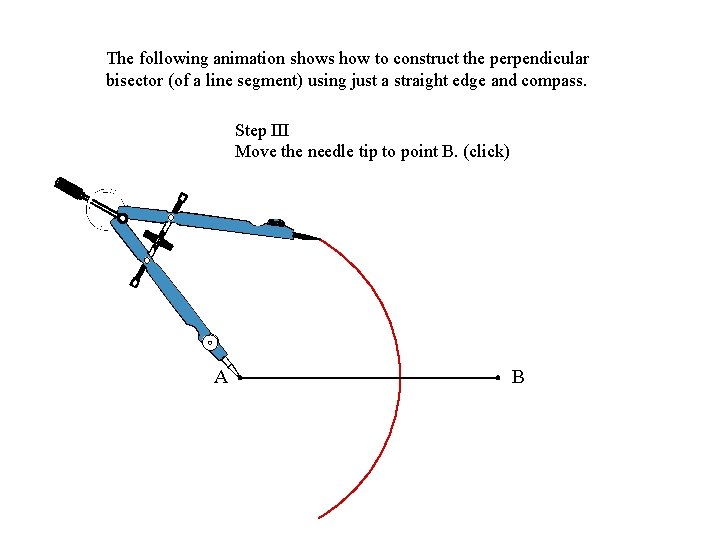
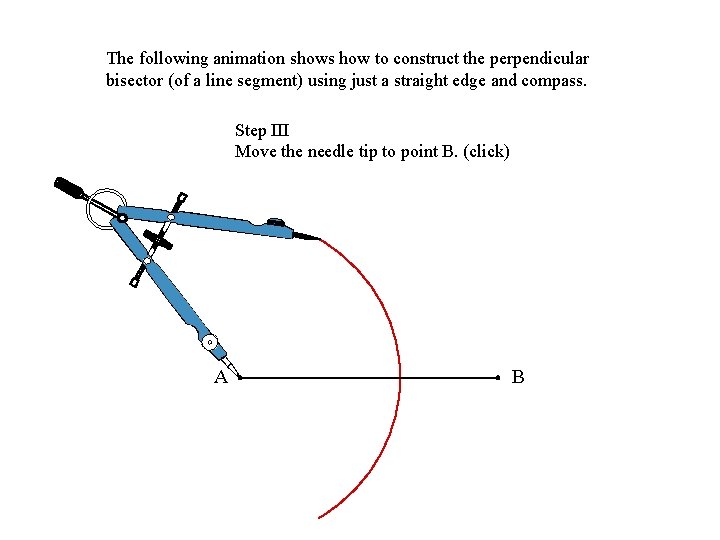
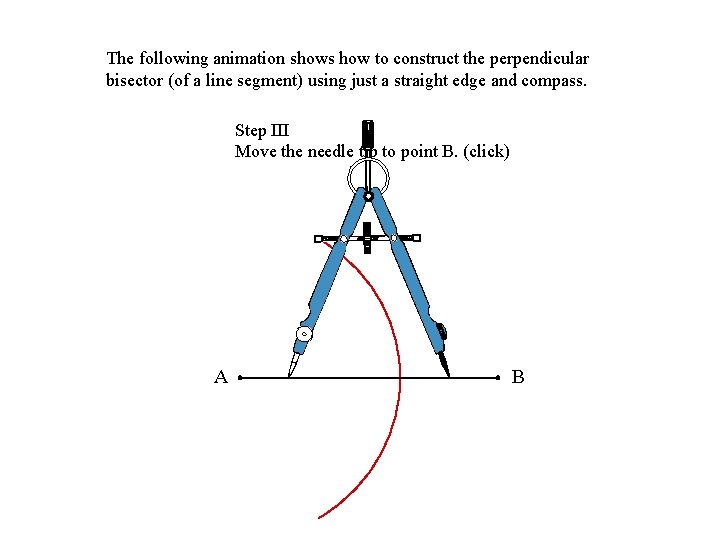
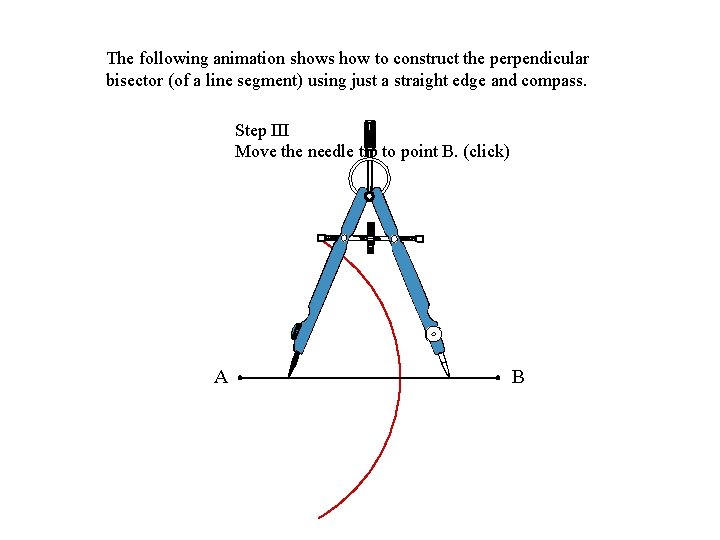
The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step III Move the needle tip to point B. (click) A B

The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step III Move the needle tip to point B. (click) A B

The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step III Move the needle tip to point B. (click) A B

The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step III Move the needle tip to point B. (click) A B

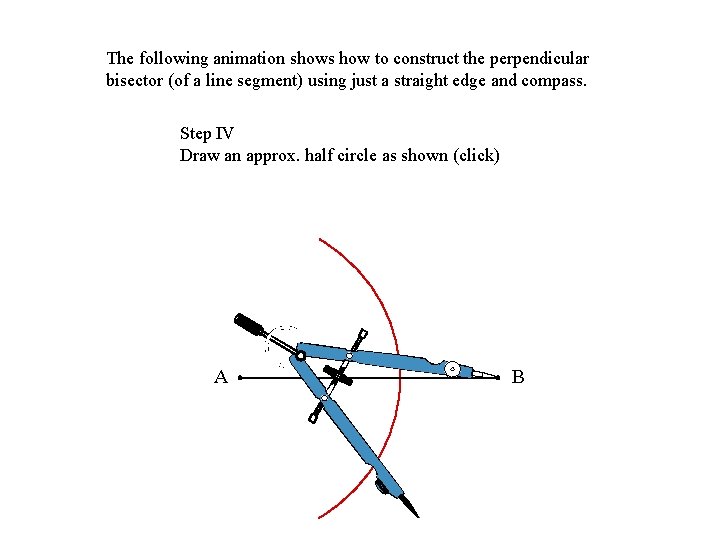
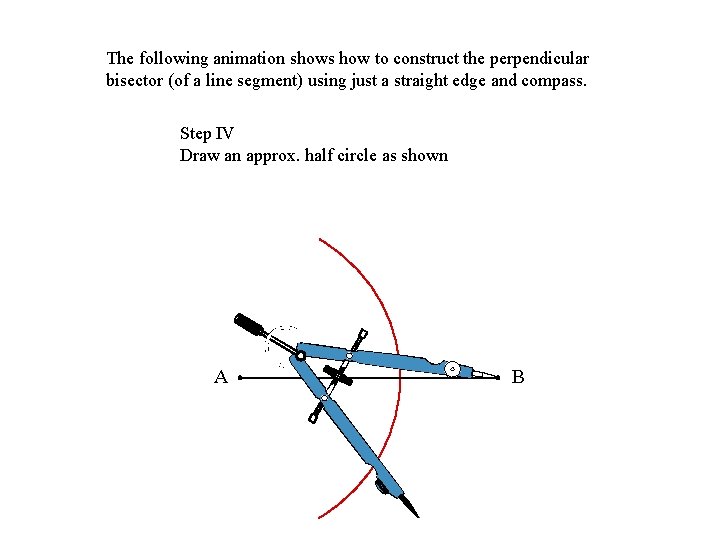
The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step IV Draw an approx. half circle as shown (click) A B

The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step IV Draw an approx. half circle as shown A B

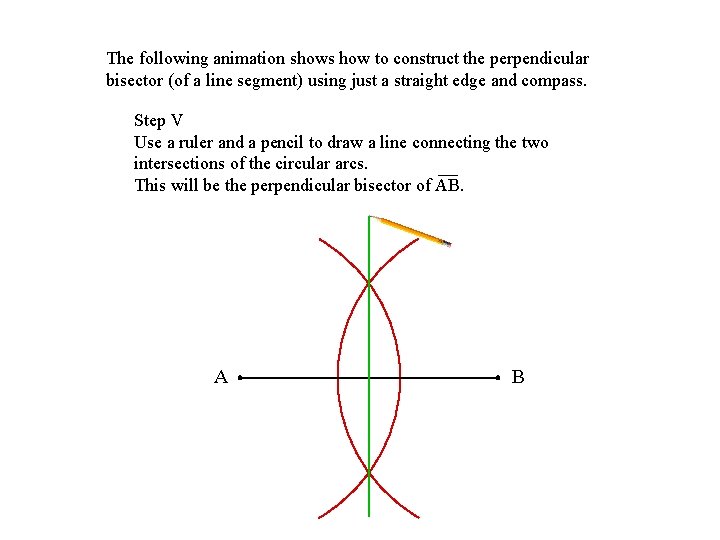
The following animation shows how to construct the perpendicular bisector (of a line segment) using just a straight edge and compass. Step V Use a ruler and a pencil to draw a line connecting the two intersections of the circular arcs. This will be the perpendicular bisector of AB. A B

Standard examples 1. Construction of an equilateral triangle, hence the construction of a 60 o angles 2. Construction of a right angle. 3. Construction of a square. 4. Bisect a given angle. 5. Construction of a line segment parallel to a given line segment. 6. Given a unit segment and any positive integer n, construction of a line segment whose length is n units. 7. Divide any given line segment into any given (whole) number of congruent parts. 8. Locating the exact centre of a given circle. 9. Given a unit segment and any positive real number x, construction of a segment whose length is square root of x times the unit segment. 10. Given a unit segment and any positive real number x, construction of a segment whose length is 1/x times the unit segment.

Construction of Regular Polygons (by compass and straight edge) 1. 2. Is it possible to construct an equilateral triangle? Is it possible to construct a square? Yes 3. Is it possible to construct a regular pentagon? Yes 4. Is it possible to construct a regular hexagon? Yes 5. Is it possible to construct a regular heptagon? No 6. Is it possible to construct a regular octagon? Yes

Important Theorem A regular n-sided polygon is constructible if and only if one of the following is true. (1) n is a power of two (but bigger than 2), or (2) n is an odd prime from the list 3, 5, 17, … (where the general form is 22 k + 1 for some whole number k. ) (3) n is of the form 2 mp 1 p 2…pr where m is a whole number and p ’s are distinct odd i primes of the above form. Examples: A regular polygon with 30 sides is constructible, but one with 35 sides will not be constructible. A regular polygon of 36 sides is also not constructible.

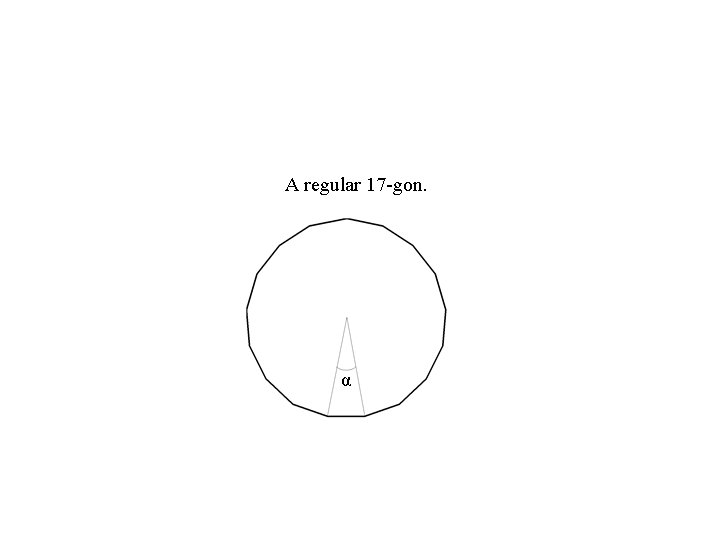
A regular 17 -gon. α

What kind of regular polygons are constructible? 1. Any equilateral triangle is constructible. 2. Any square is constructible. 3. Any regular pentagon is constructible. (see lab 20) 4. Any regular hexagon is constructible. 5. Is a regular heptagon constructible? Why? No, because 7 is a prime not on the list of the previous theorem. 6. Is a regular octagon constructible? Why? Yes, because 8 is a power of 2, and the previous theorem says that it can be done.

What kind of regular polygons are constructible? 7. Is a regular nonagon constructible? Why? No, b/c 9 = 3× 3, the 3 is repeating. 8. Is a regular decagon constructible? Why? Yes, b/c 10 = 2× 5, and 5 is on the list. 9. Is a regular 11 -gon constructible? Why? No, b/c 11 is a prime but not on the list. 10. Is a regular 12 -gon constructible? Why? Yes, b/c 12 = 2× 2× 3 and 3 is on the list. 11. Is a regular 13 -gon constructible? Why? No, b/c 13 is a prime but not on the list. 12. Is a regular 14 -gon constructible? Why? No, b/c 14 = 2× 7 but 7 is an odd prime not on the list.

Constructible Angles We know that angles with measures of 90°, 60°, 45°, 30° are all constructible by straight edge and compass (see Lab 20). 1. Is it possible to construct a 75° angle (with straight edge and compass)? Yes, b/c 75° = 45° + 30° 2. Is it possible to construct a 15° angle (with straight edge and compass)? Yes, b/c 15° = 45° – 30°, and 15° = 30° ÷ 2

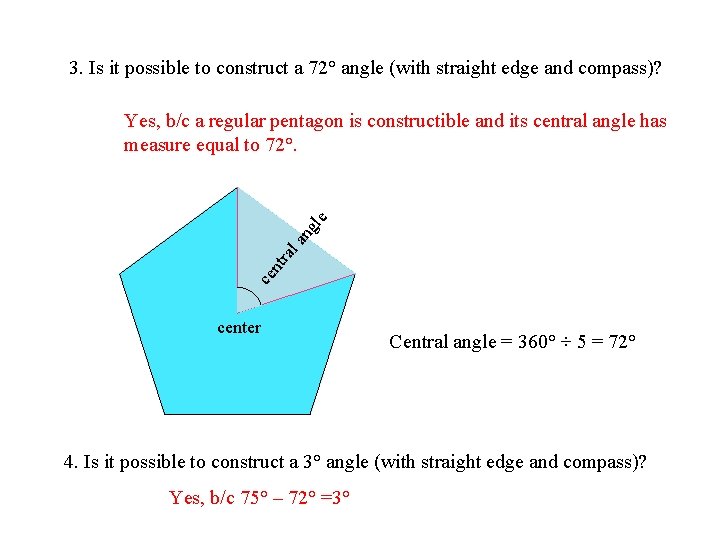
3. Is it possible to construct a 72° angle (with straight edge and compass)? ce nt ra l a ng le Yes, b/c a regular pentagon is constructible and its central angle has measure equal to 72°. center Central angle = 360° ÷ 5 = 72° 4. Is it possible to construct a 3° angle (with straight edge and compass)? Yes, b/c 75° – 72° =3°

5. Is it possible to construct a 40° angle (with straight edge and compass)? θ No, b/c the central angle θ of a regular nonagon is exactly 360° ÷ 9 = 40°, and from a previous result, we know that a regular nonagon is not constructible. 6. Is it possible to construct a 1° angle (with straight edge and compass)? No, b/c otherwise we can construct a 40° angle by repeated addition of angles.

Conclusion I. The smallest constructible angle with positive integer degree measure is a 3° angle. II. If n is a positive integer, and angle A has measure n°, then angle A is constructible if and only if n is a multiple of 3. Remark: Conclusion II above does not apply to angles with non-integer degree measures. For instance, a 7. 5° angle is constructible, but 7. 5 is not a multiple of 3. Example: Can we construct an 14° angle with just straight edge and compass?

What cannot be done? 1. Trisect an angle whose measure is not 3 times of an angle which is already constructible by another method, for instance, 90 o can be trisected because a 30 o angle is constructible by bisecting a 60 o angle. However a 30° angle cannot be trisected. 2. Square a circle: i. e. construct a square with the same area as a given circle. (consequently, circling a square is also impossible. ) 3. Construct a line segment whose length is 3 2 times a given unit line segment.

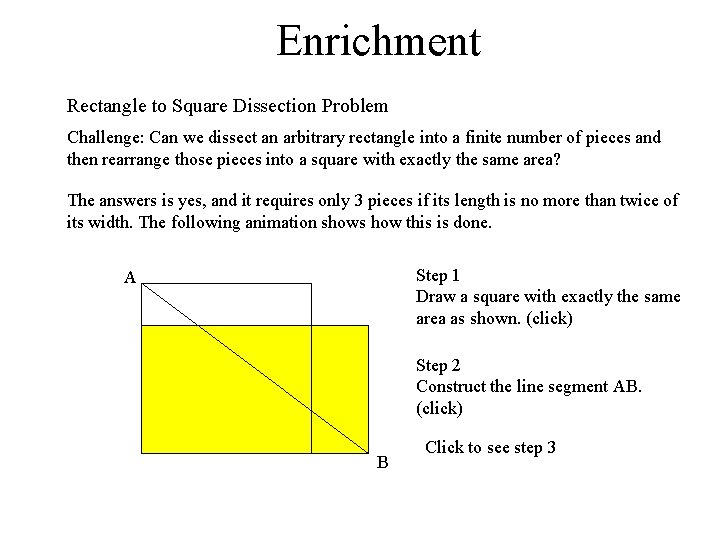
Enrichment Rectangle to Square Dissection Problem Challenge: Can we dissect an arbitrary rectangle into a finite number of pieces and then rearrange those pieces into a square with exactly the same area? The answers is yes, and it requires only 3 pieces if its length is no more than twice of its width. The following animation shows how this is done. Step 1 Draw a square with exactly the same area as shown. (click) A Step 2 Construct the line segment AB. (click) B Click to see step 3

Rectangle to Square Dissection Problem Challenge: Can we dissect an arbitrary rectangle into a finite number of pieces and then rearrange those pieces into a square with exactly the same area? The answers is yes, and it requires only 3 pieces if its length is no more than 4 times of its width. The following animation shows how this is done. Step 1 Draw a square with exactly the same area as shown. (click) Step 3 Slide the triangles up. (click) Step 2 Construct the line segment AB. (click)

If the length is more than 4 times of the width, we first cut the rectangle into two congruent shorter pieces and then rearrange them into a rectangle with shorter length. (click to see animation)

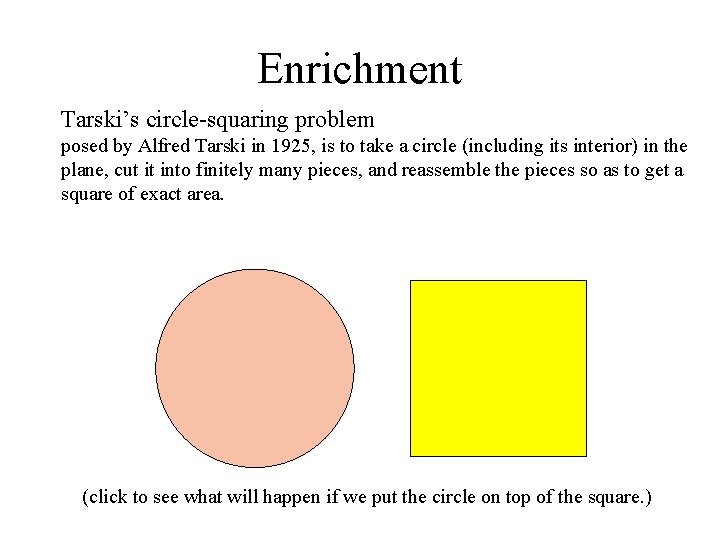
Enrichment Tarski’s circle-squaring problem posed by Alfred Tarski in 1925, is to take a circle (including its interior) in the plane, cut it into finitely many pieces, and reassemble the pieces so as to get a square of exact area. (click to see what will happen if we put the circle on top of the square. )

A partial solution was given by Miklos Laczkovich in 1990; whose decomposition consists of about 1050 different pieces, but the pieces do not have nice boundaries (i. e. not Jordan curves) and hence cannot be cut out with scissors. It might be possible that some day, some one will give a better solution to this problem.

Section 14. 5 Geometric Problem Solving using Triangle Congruence and Similarity In this section, we apply triangle congruence and similarity to prove properties of geometric shape. Many of these properties have been observed informally in Chapter 12.

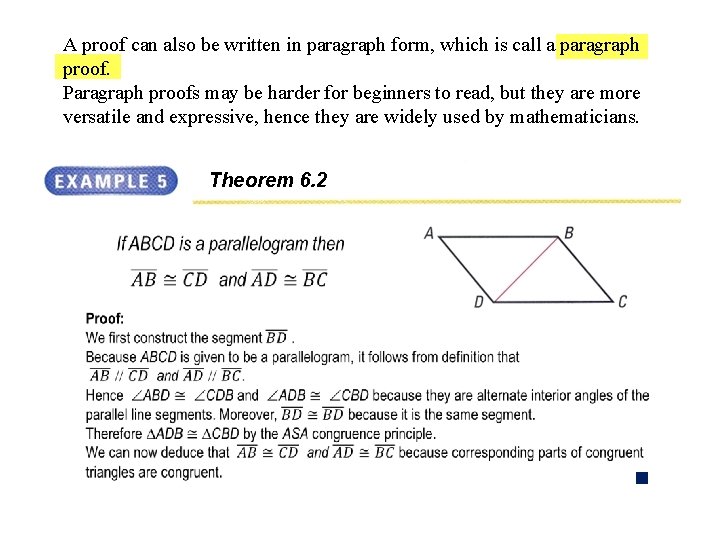
Loosely speaking, a mathematical proof is a valid logical argument for a mathematical statement. A two column proof is an argument presented in a table with 2 columns, where statements and reasons are numbered to show their order in the argument.

A proof can also be written in paragraph form, which is call a paragraph proof. Paragraph proofs may be harder for beginners to read, but they are more versatile and expressive, hence they are widely used by mathematicians. Theorem 6. 2

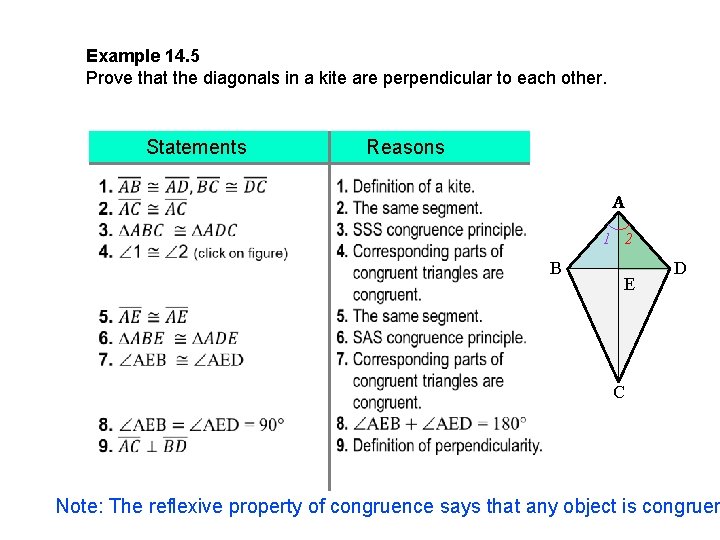
Example 14. 5 Prove that the diagonals in a kite are perpendicular to each other. Statements Reasons A 1 2 B E D C Note: The reflexive property of congruence says that any object is congruen

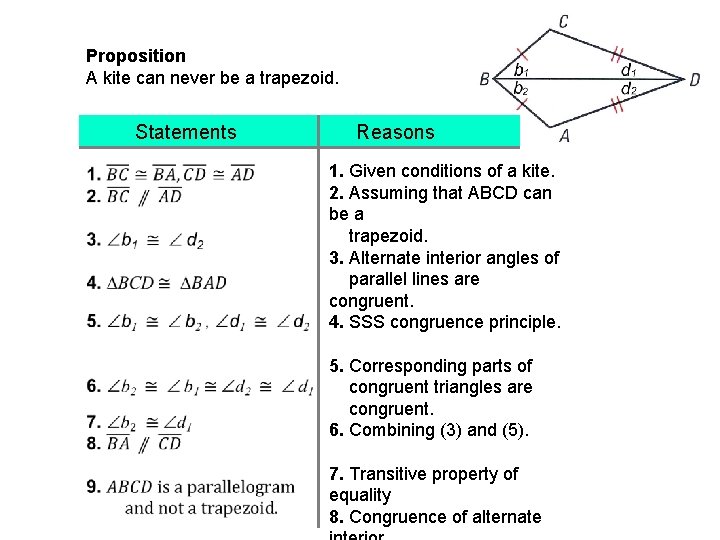
Proposition A kite can never be a trapezoid. Statements Reasons 1. Given conditions of a kite. 2. Assuming that ABCD can be a trapezoid. 3. Alternate interior angles of parallel lines are congruent. 4. SSS congruence principle. 5. Corresponding parts of congruent triangles are congruent. 6. Combining (3) and (5). 7. Transitive property of equality 8. Congruence of alternate

Statements Reasons 1. Given 2. The same angle. 3. Given 4. SAS similarity principle 5. Corresponding angles of similar triangles are congruent. 6. Converse of corresponding angle theorem for parallel lines. 7. Corresponding sides of similar triangles are in same ratio.

We call PQRS the midquad of ABCD because it is a quadrilateral formed by joining the midpoints of the sides of ABCD.

Statements Reasons 1. For any two points, we can connect a line segment. 2. Midsegment theorem for ABC. 3. Midsegment theorem for ADC. 4. Transitive property for parallel lines. 5. Similar reasons as (1) to (4).