Starter Use the Sine rule and Cosine rule






- Slides: 17


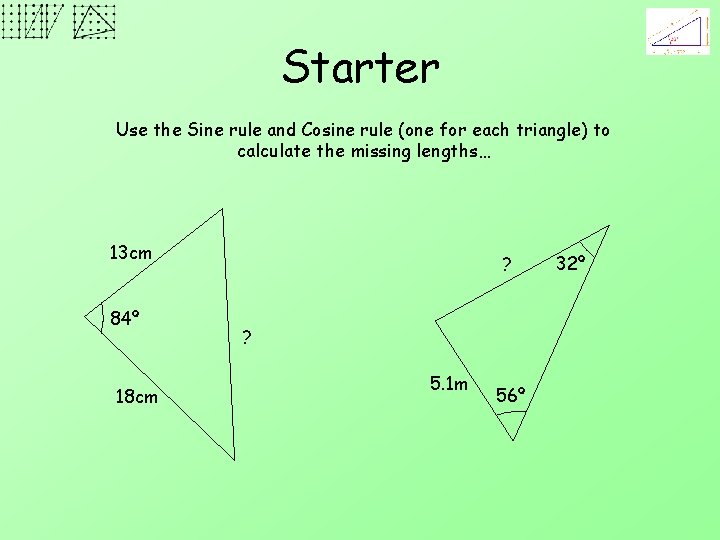
Starter Use the Sine rule and Cosine rule (one for each triangle) to calculate the missing lengths… 13 cm 84º 18 cm ? ? 5. 1 m 56º 32º

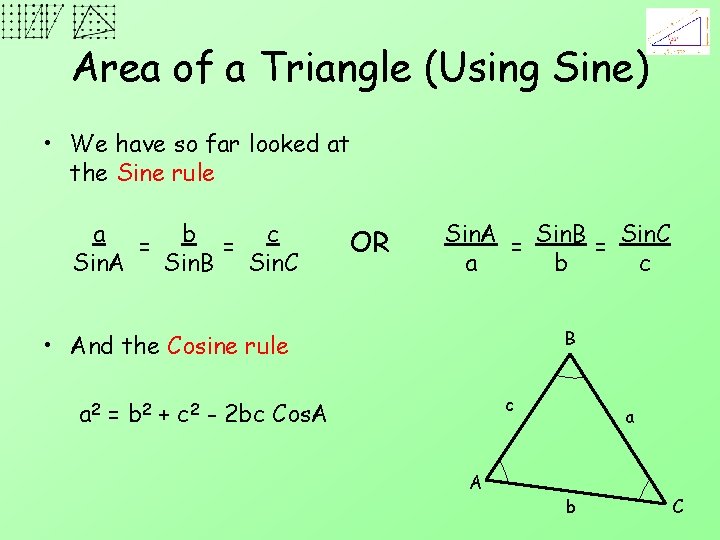
Area of a Triangle (Using Sine) • We have so far looked at the Sine rule a = b = c Sin. A Sin. B Sin. C OR Sin. A = Sin. B = Sin. C a b c B • And the Cosine rule c a 2 = b 2 + c 2 - 2 bc Cos. A A a b C

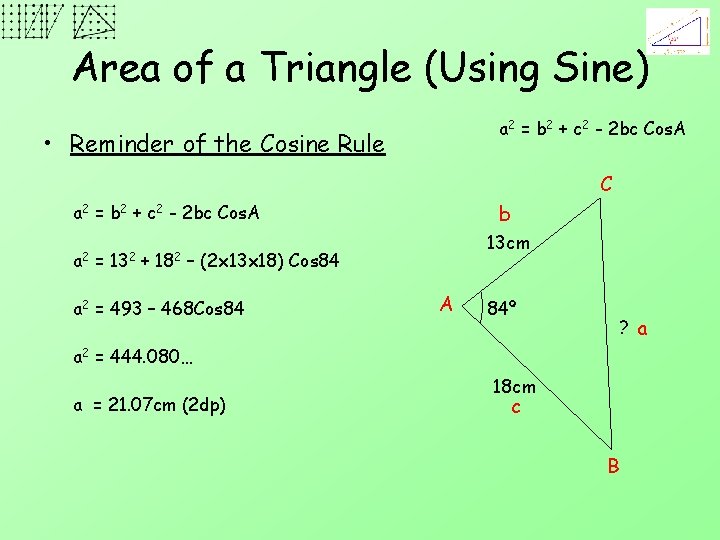
Area of a Triangle (Using Sine) a 2 = b 2 + c 2 - 2 bc Cos. A • Reminder of the Cosine Rule C b a 2 = b 2 + c 2 - 2 bc Cos. A a 2 = 132 + 182 13 cm – (2 x 13 x 18) Cos 84 a 2 = 493 – 468 Cos 84 A 84º ? a a 2 = 444. 080… a = 21. 07 cm (2 dp) 18 cm c B

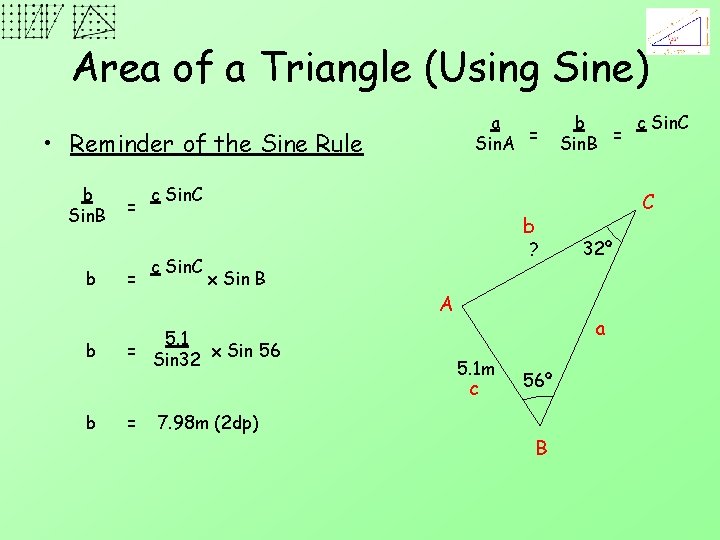
Area of a Triangle (Using Sine) a = Sin. A • Reminder of the Sine Rule b Sin. B = c Sin. C ? = b 5. 1 = x Sin 56 Sin 32 x Sin B A 7. 98 m (2 dp) 32º a 5. 1 m c = C b b c Sin. C = Sin. B 56º B

Area of a Triangle (Using Sine) • The formula for the area of a triangle is; 1/ 2 base x height OR (base x height) ÷ 2 This relies on us knowing the perpendicular height though Another formula you can use is; 1/ 2 ab. Sin. C (1/2 x a x b x Sin. C)

Area of a Triangle (Using Sine) Learning Objectives All will be able to recognise appropriate situations to use the formula for the area of a triangle using Sine (Grade A) Most will be able to then correctly use the formula to calculate areas (Grade A) Some will then be able to use this in the context of a harder question, such as finding the area of a segment (Grade A*)

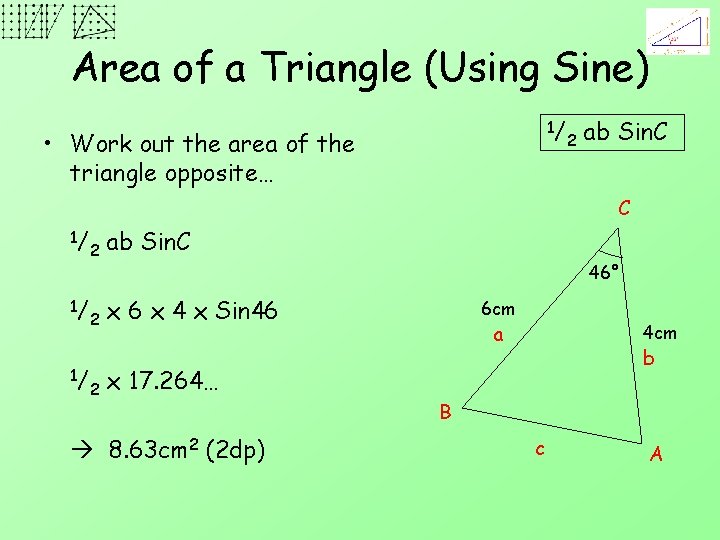
Area of a Triangle (Using Sine) 1/ • Work out the area of the triangle opposite… 2 ab Sin. C C 1/ 1/ 1/ 2 ab Sin. C 2 x 6 x 4 x Sin 46 2 46° 6 cm a 4 cm b x 17. 264… 8. 63 cm 2 (2 dp) B c A

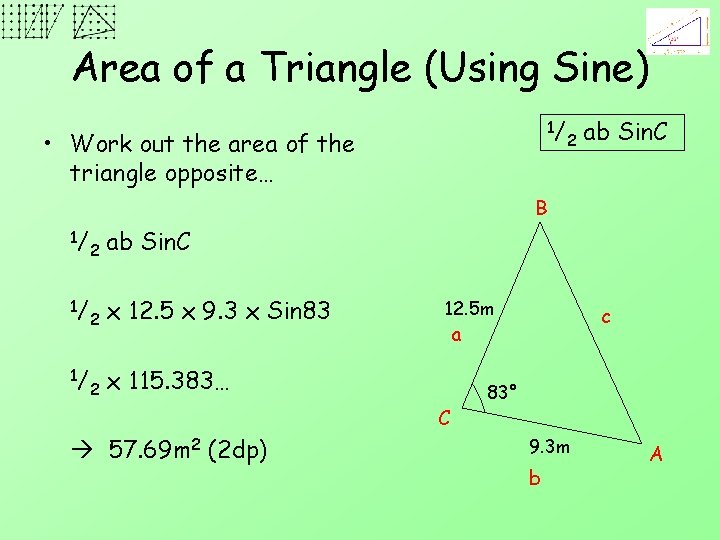
Area of a Triangle (Using Sine) 1/ • Work out the area of the triangle opposite… 2 ab Sin. C B 1/ 2 ab Sin. C 1/ 2 x 12. 5 x 9. 3 x Sin 83 1/ 2 x 115. 383… 12. 5 m a C 57. 69 m 2 (2 dp) c 83° 9. 3 m b A

Plenary B c a C 60º 5 cm b A Area = 1/2 ab sin C Area = 1/2 (5 x 5) sin 60 Area = 1/2 25 sin 60 Area = 1/2 21. 65… Area = 10. 825… 32. 48

Area of a Triangle (Using Sine) Learning Objectives All will be able to recognise appropriate situations to use the formula for the area of a triangle using Sine (Grade A) Most will be able to then correctly use the formula to calculate areas (Grade A) Some will then be able to use this in the context of a harder question, such as finding the area of a segment (Grade A*)

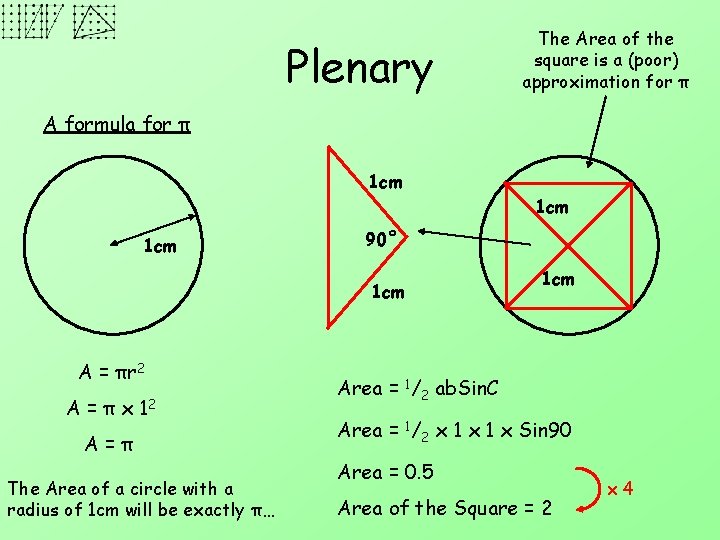
Plenary The Area of the square is a (poor) approximation for π A formula for π 1 cm 1 cm 90˚ 1 cm A = πr 2 A = π x 12 A=π The Area of a circle with a radius of 1 cm will be exactly π… 1 cm Area = 1/2 ab. Sin. C Area = 1/2 x 1 x Sin 90 Area = 0. 5 Area of the Square = 2 x 4

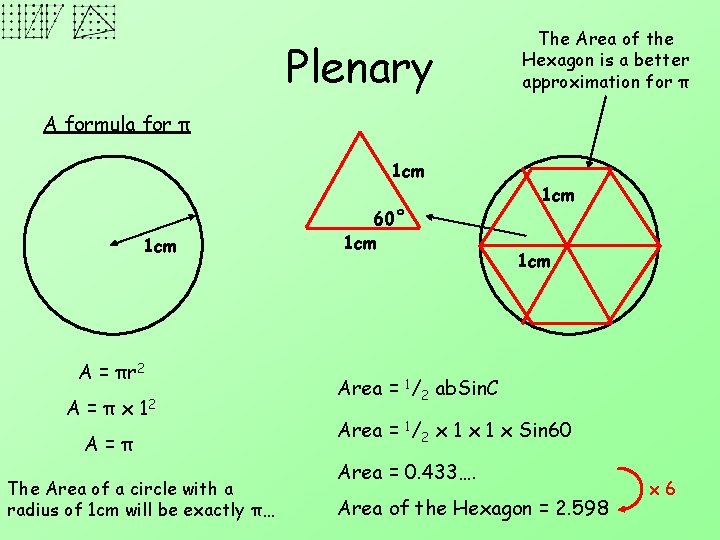
Plenary The Area of the Hexagon is a better approximation for π A formula for π 1 cm A = πr 2 A = π x 12 A=π The Area of a circle with a radius of 1 cm will be exactly π… 60˚ 1 cm 1 cm Area = 1/2 ab. Sin. C Area = 1/2 x 1 x Sin 60 Area = 0. 433…. Area of the Hexagon = 2. 598 x 6

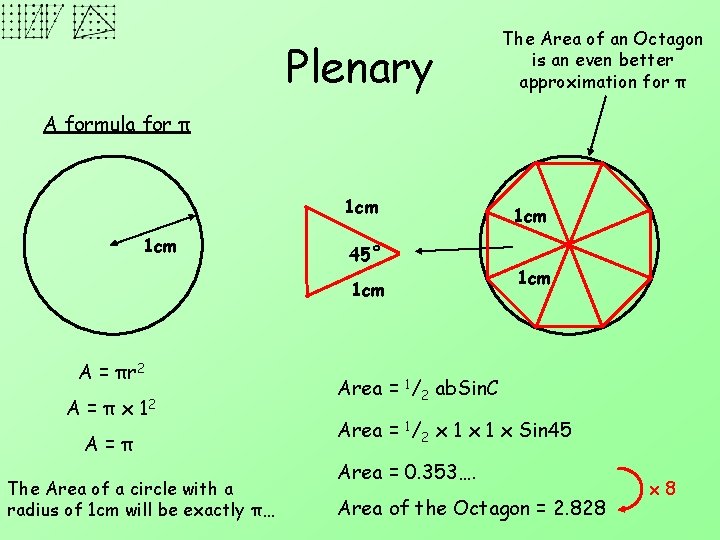
Plenary The Area of an Octagon is an even better approximation for π A formula for π 1 cm 45˚ 1 cm A = πr 2 A = π x 12 A=π The Area of a circle with a radius of 1 cm will be exactly π… 1 cm Area = 1/2 ab. Sin. C Area = 1/2 x 1 x Sin 45 Area = 0. 353…. Area of the Octagon = 2. 828 x 8

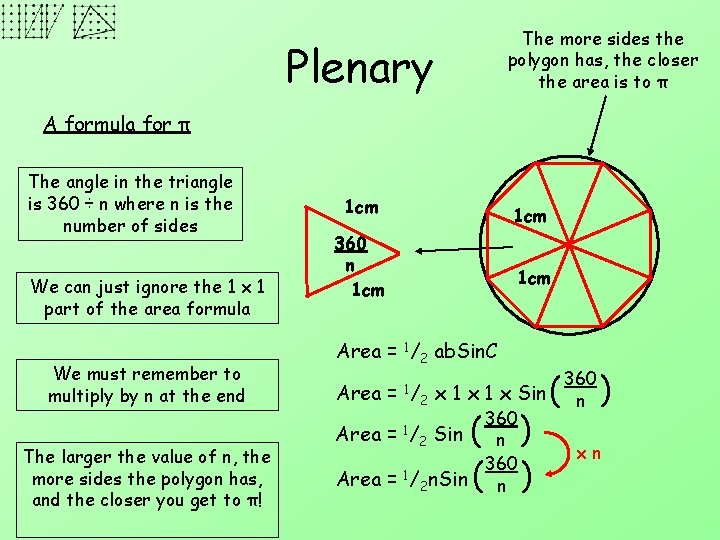
The more sides the polygon has, the closer the area is to π Plenary A formula for π The angle in the triangle is 360 ÷ n where n is the number of sides We can just ignore the 1 x 1 part of the area formula We must remember to multiply by n at the end The larger the value of n, the more sides the polygon has, and the closer you get to π! 1 cm 360 n 1 cm Area = 1/2 ab. Sin. C ) 360 Area = 2 x 1 x Sin n 360 1 Area = /2 Sin n xn 360 Area = 1/2 n. Sin n 1/ ( ( ) ) (

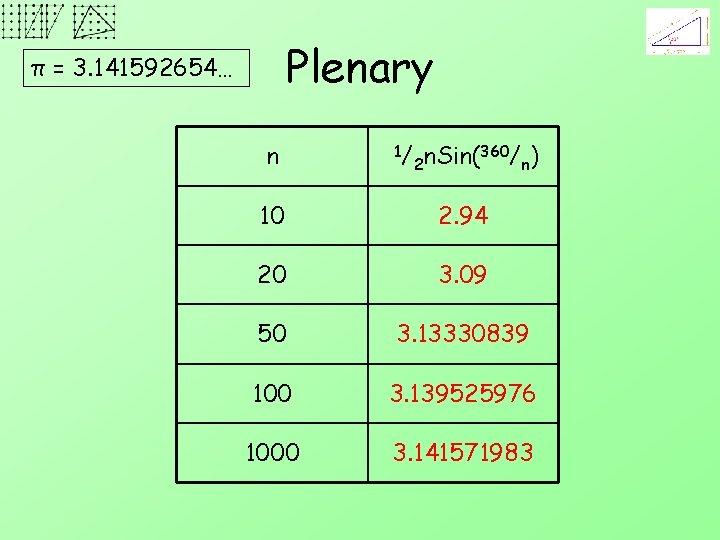
Plenary π = 3. 141592654… n 1/ 2 n. Sin( 360/ n) 10 2. 94 20 3. 09 50 3. 13330839 100 3. 139525976 1000 3. 141571983

Summary • We have recapped using the Sine and Cosine Rules • We have seen how to find the area of a triangle without the perpendicular height • Some questions involved using several rules one at a time
 When do we use cosine rule
When do we use cosine rule Sine and cosine rule
Sine and cosine rule Sine rule and cosine rule
Sine rule and cosine rule Magic triangle trigonometry
Magic triangle trigonometry When to use cosine rule
When to use cosine rule Dr frost sine and cosine rule
Dr frost sine and cosine rule Sine and cosine graphs
Sine and cosine graphs How to find period of cosine function
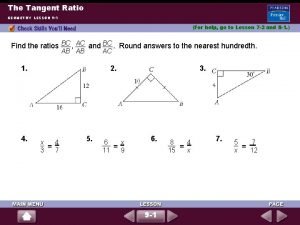
How to find period of cosine function Lesson 13-2 sine and cosine ratios answer key
Lesson 13-2 sine and cosine ratios answer key Sine maze
Sine maze Graphing sine and cosine quiz
Graphing sine and cosine quiz 4-4 graphing sine and cosine functions
4-4 graphing sine and cosine functions Sin inverse sin x is equal to
Sin inverse sin x is equal to Graph of sine and cosine functions
Graph of sine and cosine functions Sine word problems
Sine word problems Practice 8-4 sine and cosine ratios
Practice 8-4 sine and cosine ratios Sine and cosine ratios
Sine and cosine ratios 6-5 practice translations of sine and cosine functions
6-5 practice translations of sine and cosine functions