Lesson 5 3 Proving Triangles Similar AA SSS

AA Similarity (Angle-Angle) If 2 angles of one triangle are congruent to 2 angles

SSS Similarity (Side-Side) If the measures of the corresponding sides of 2 triangles are

SAS Similarity (Side-Angle-Side) If the measures of 2 sides of a triangle are proportional

Proving Triangles Similarity is reflexive, symmetric, and transitive. Steps for proving triangles similar: 1.

Problem #1 Step 1: Mark the given … and what it implies Step 2:

Problem #2 Step 1: Mark the given … and what it implies Step 2:

Problem #3 Step 1: Mark the given … and what it implies Step 2:

1. Statements G is the Midpoint of H is the Midpoint of Reasons Given

Slides: 9

Download presentation

Lesson 5 -3 Proving Triangles Similar (AA, SSS, SAS) Lesson 5 -3: Proving Triangles Similar 1

AA Similarity (Angle-Angle) If 2 angles of one triangle are congruent to 2 angles of another triangle, then the triangles are similar. Given: and Conclusion: Lesson 5 -3: Proving Triangles Similar 2

SSS Similarity (Side-Side) If the measures of the corresponding sides of 2 triangles are proportional, then the triangles are similar. 5 8 11 10 16 22 Given: Conclusion: Lesson 5 -3: Proving Triangles Similar 3

SAS Similarity (Side-Angle-Side) If the measures of 2 sides of a triangle are proportional to the measures of 2 corresponding sides of another triangle and the angles between them are congruent, then the triangles are similar. 5 10 11 22 Given: Conclusion: Lesson 5 -3: Proving Triangles Similar 4

Proving Triangles Similarity is reflexive, symmetric, and transitive. Steps for proving triangles similar: 1. Mark the Given. 2. Mark … Shared Angles or Vertical Angles 3. Choose a Method. (AA, SSS , SAS) Think about what you need for the chosen method and be sure to include those parts in the proof. Lesson 5 -3: Proving Triangles Similar 5

Problem #1 Step 1: Mark the given … and what it implies Step 2: Mark the vertical angles Step 3: Choose a method: (AA, SSS, SAS) Step 4: List the Parts in the order of the method with reasons Step 5: Is there more? Statements Reasons AA Given G D Alternate Interior <s C Alternate Interior <s E AA Similarity F Lesson 5 -3: Proving Triangles Similar 6

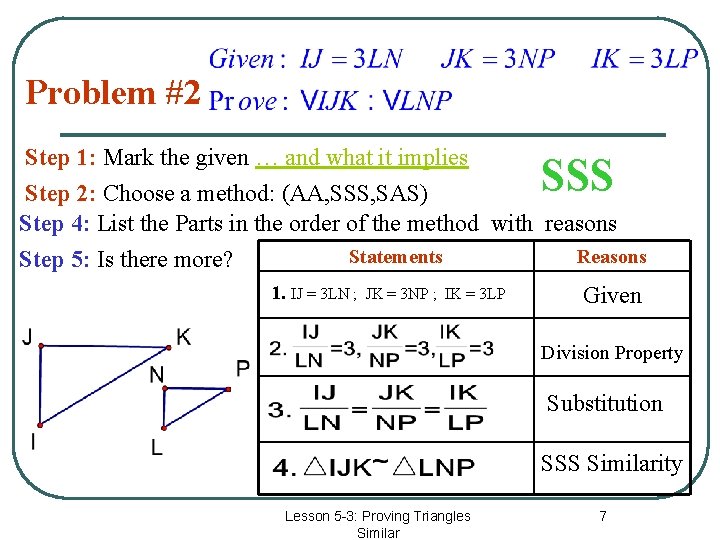
Problem #2 Step 1: Mark the given … and what it implies Step 2: Choose a method: (AA, SSS, SAS) Step 4: List the Parts in the order of the method with reasons Statements Reasons Step 5: Is there more? 1. IJ = 3 LN ; JK = 3 NP ; IK = 3 LP Given SSS Division Property Substitution SSS Similarity Lesson 5 -3: Proving Triangles Similar 7

Problem #3 Step 1: Mark the given … and what it implies Step 2: Mark the reflexive angles Step 3: Choose a method: (AA, SSS, SAS) SAS Step 4: List the Parts in the order of the method with reasons Next Slide…………. Step 5: Is there more? Lesson 5 -3: Proving Triangles Similar 8

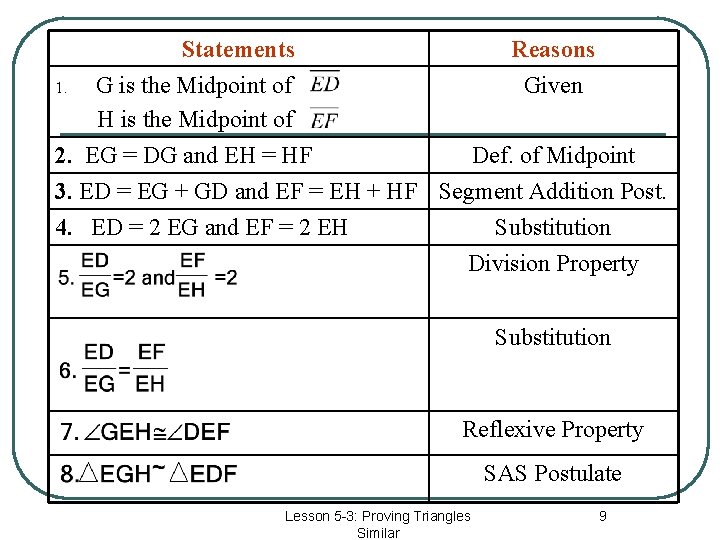
1. Statements G is the Midpoint of H is the Midpoint of Reasons Given 2. EG = DG and EH = HF Def. of Midpoint 3. ED = EG + GD and EF = EH + HF Segment Addition Post. 4. ED = 2 EG and EF = 2 EH Substitution Division Property Substitution Reflexive Property SAS Postulate Lesson 5 -3: Proving Triangles Similar 9