Proving Triangles Similar Lesson 5 3 AA SSS

Proving Triangles Similar Lesson 5 -3 (AA~, SSS~, SAS~)

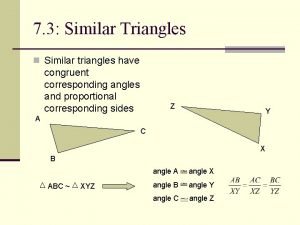
Similar Triangles Two triangles are similar if they are the same shape. That means the vertices can be paired up so the angles are congruent. Size does not matter.

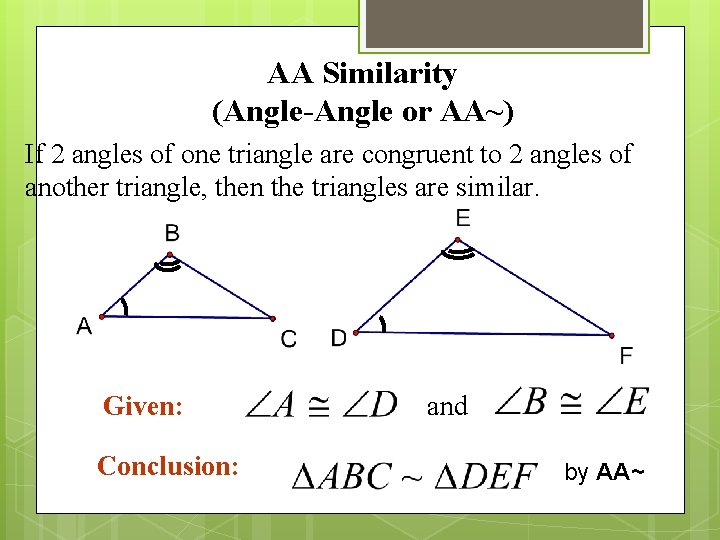
AA Similarity (Angle-Angle or AA~) If 2 angles of one triangle are congruent to 2 angles of another triangle, then the triangles are similar. Given: Conclusion: and by AA~

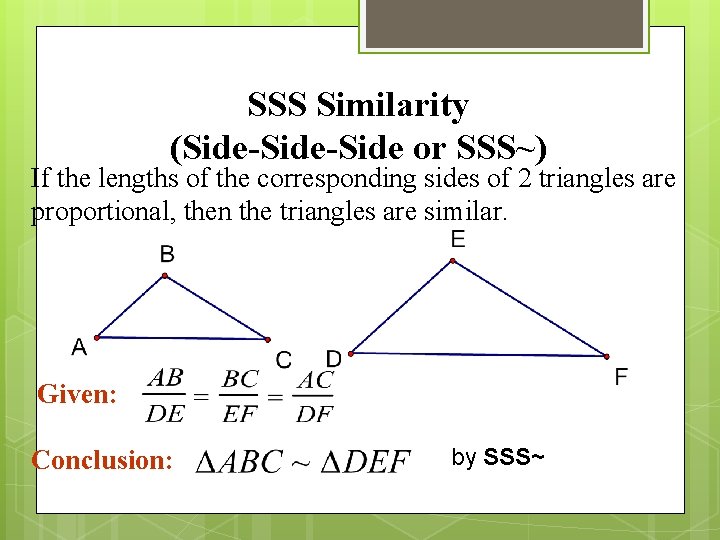
SSS Similarity (Side-Side or SSS~) If the lengths of the corresponding sides of 2 triangles are proportional, then the triangles are similar. Given: Conclusion: by SSS~

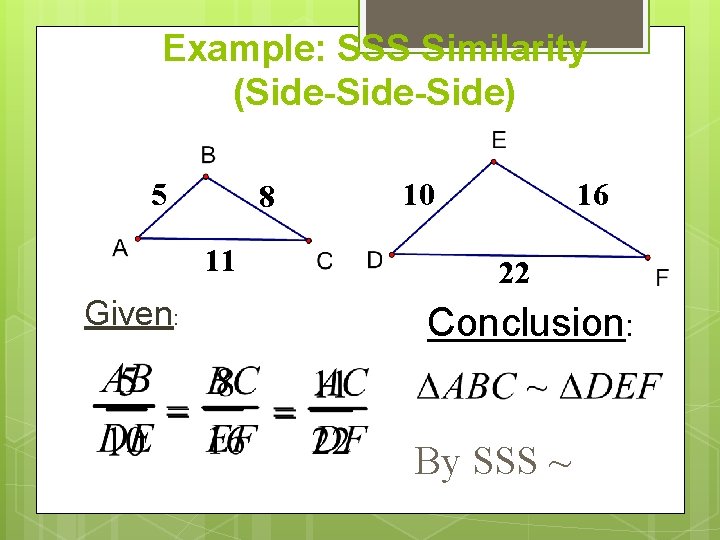
Example: SSS Similarity (Side-Side) 5 8 11 Given: 10 16 22 Conclusion: By SSS ~

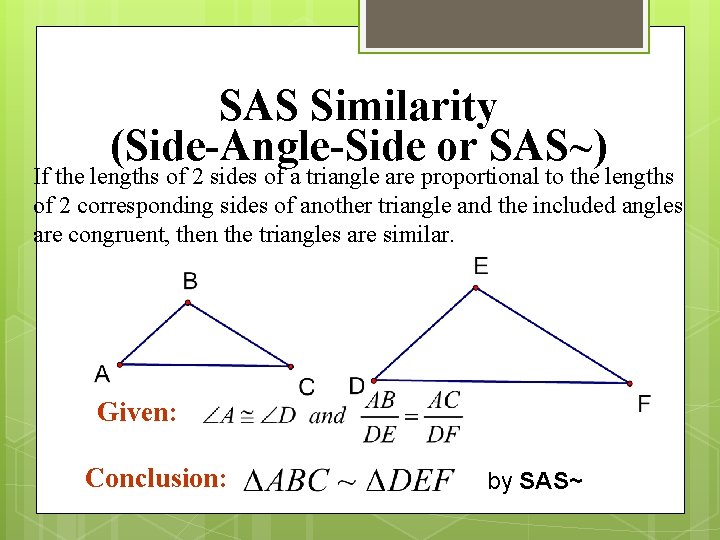
SAS Similarity (Side-Angle-Side or SAS~) If the lengths of 2 sides of a triangle are proportional to the lengths of 2 corresponding sides of another triangle and the included angles are congruent, then the triangles are similar. Given: Conclusion: by SAS~

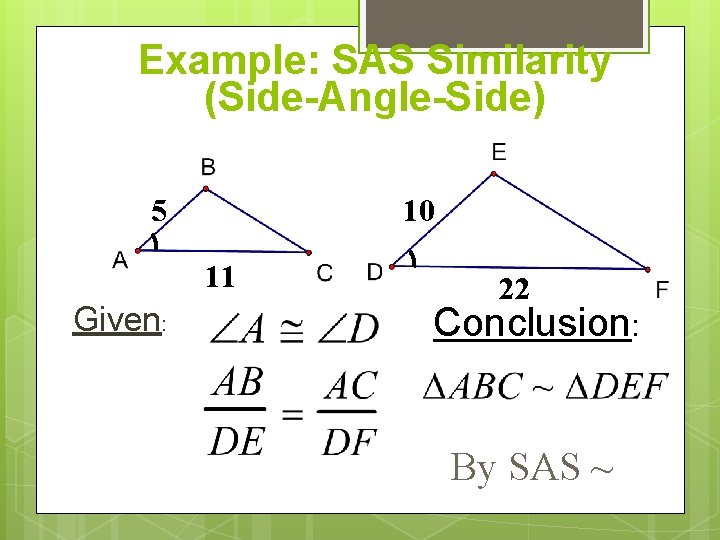
Example: SAS Similarity (Side-Angle-Side) 5 10 11 Given: 22 Conclusion: By SAS ~

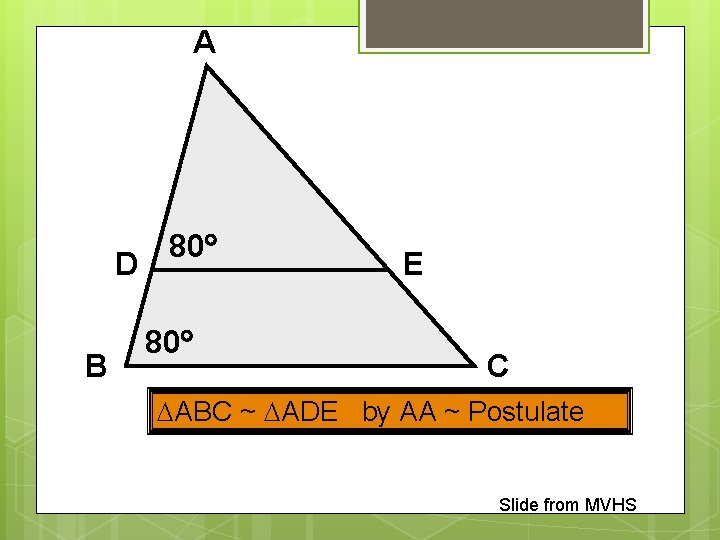
A D B 80 80 E C ABC ~ ADE by AA ~ Postulate Slide from MVHS

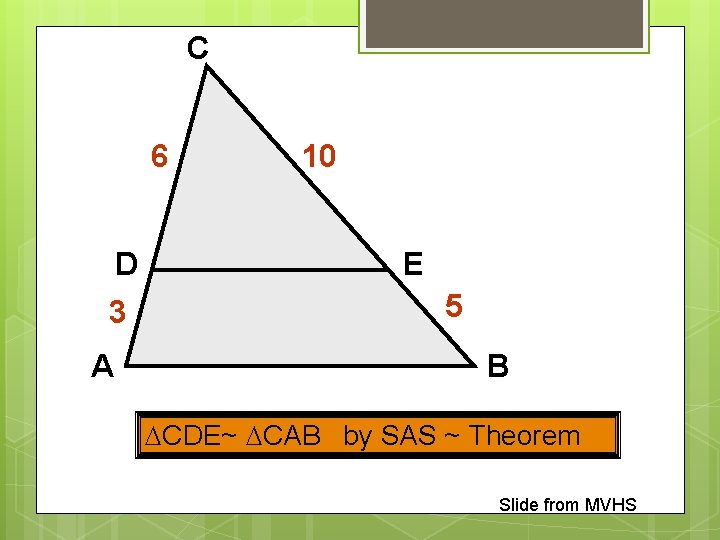
C 6 D 3 A 10 E 5 B CDE~ CAB by SAS ~ Theorem Slide from MVHS

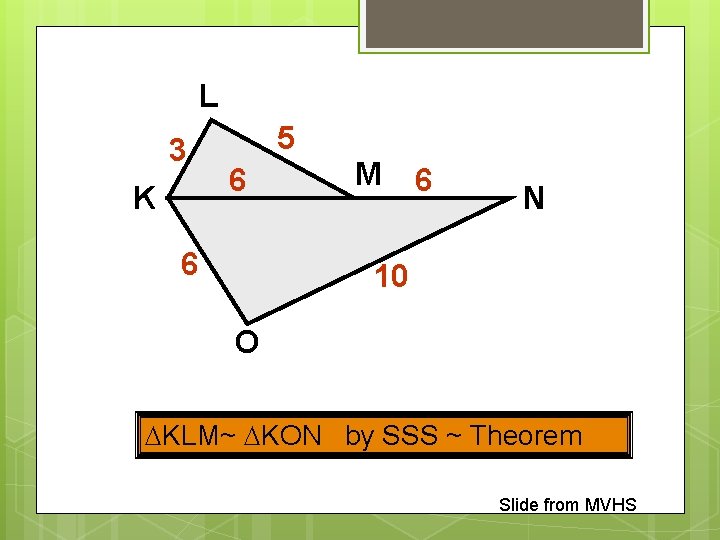
L 3 K 5 6 6 M 6 N 10 O KLM~ KON by SSS ~ Theorem Slide from MVHS

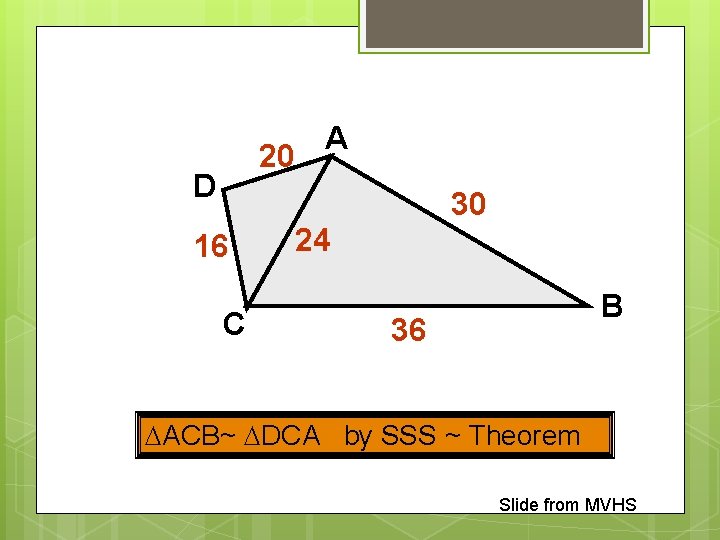
20 D A 30 16 C 24 B 36 ACB~ DCA by SSS ~ Theorem Slide from MVHS

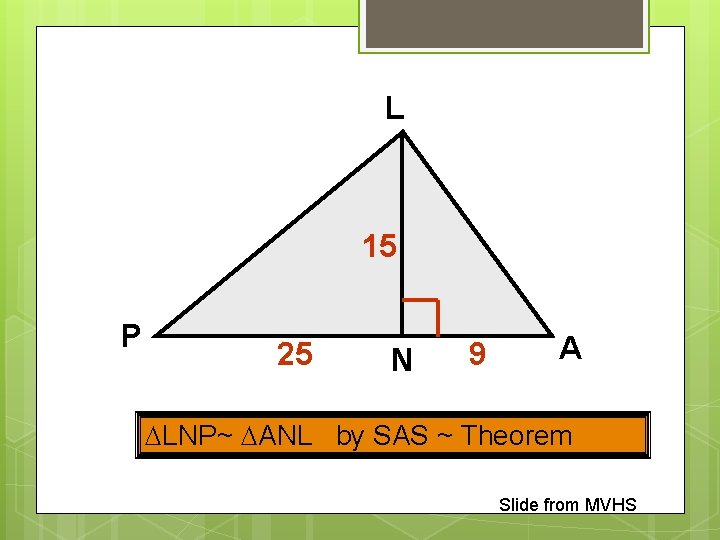
L 15 P 25 N 9 A LNP~ ANL by SAS ~ Theorem Slide from MVHS

Proving Triangles Similarity is reflexive, symmetric, and transitive. Steps for proving triangles similar: 1. Mark the Given. 2. Mark … Reflexive (shared) Angles or Vertical Angles 3. Choose a Method. (AA~, SSS~, SAS~) Think about what you need for the chosen method and be sure to include those parts in the proof.

Problem #1 Step 1: Mark the given … and what it implies Step 2: Mark the vertical angles Step 3: Choose a method: (AA, SSS, SAS) Step 4: List the Parts in the order of the method with reasons Step 5: Is there more? Statements Reasons AA G D Given Alternate Interior <s C Alternate Interior <s E F AA Similarity

Problem #2 Step 1: Mark the given … and what it implies Step 2: Choose a method: (AA, SSS, SAS) Step 4: List the Parts in the order of the method with reasons Statements Reasons Step 5: Is there more? 1. IJ = 3 LN ; JK = 3 NP ; IK = 3 LP Given SSS Division Property Substitution SSS Similarity

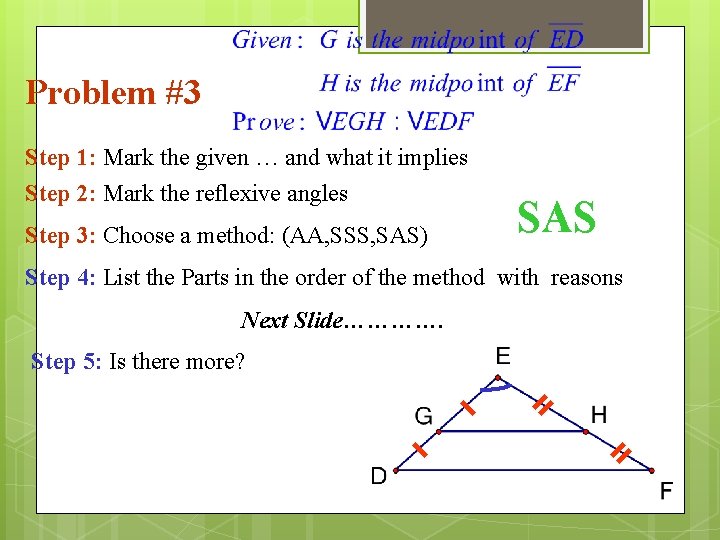
Problem #3 Step 1: Mark the given … and what it implies Step 2: Mark the reflexive angles Step 3: Choose a method: (AA, SSS, SAS) SAS Step 4: List the Parts in the order of the method with reasons Next Slide…………. Step 5: Is there more?

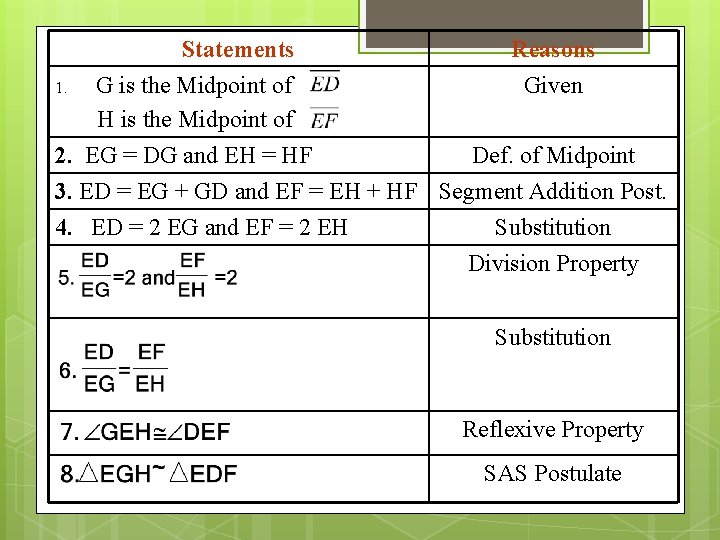
Statements Reasons 1. G is the Midpoint of Given H is the Midpoint of 2. EG = DG and EH = HF Def. of Midpoint 3. ED = EG + GD and EF = EH + HF Segment Addition Post. 4. ED = 2 EG and EF = 2 EH Substitution Division Property Substitution Reflexive Property SAS Postulate

Similarity is reflexive, symmetric, and transitive.

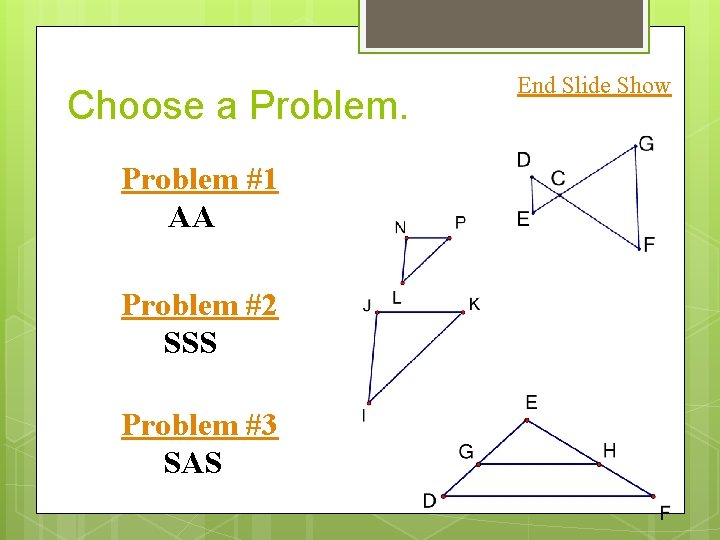
Choose a Problem #1 AA Problem #2 SSS Problem #3 SAS End Slide Show

The End 1. Mark the Given. 2. Mark … Shared Angles or Vertical Angles 3. Choose a Method. (AA, SSS , SAS) **Think about what you need for the chosen method and be sure to include those parts in the proof.