SIMILAR TRIANGLES SIMILAR TRIANGLES If two angles of
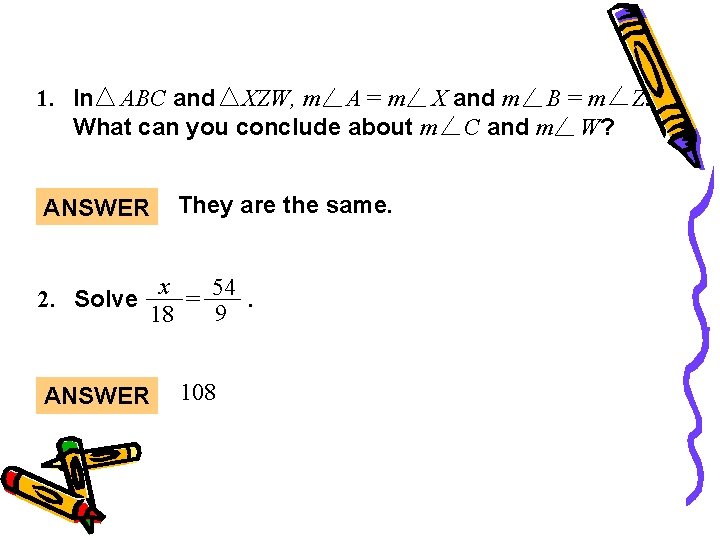







- Slides: 20

SIMILAR TRIANGLES

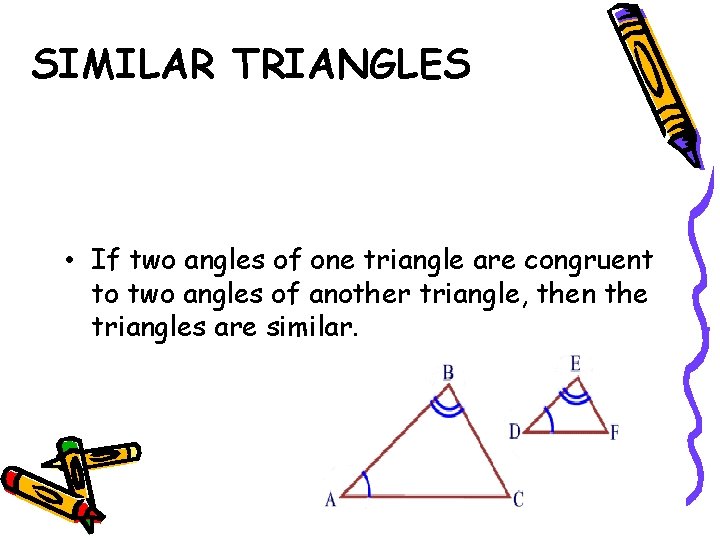
SIMILAR TRIANGLES • If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
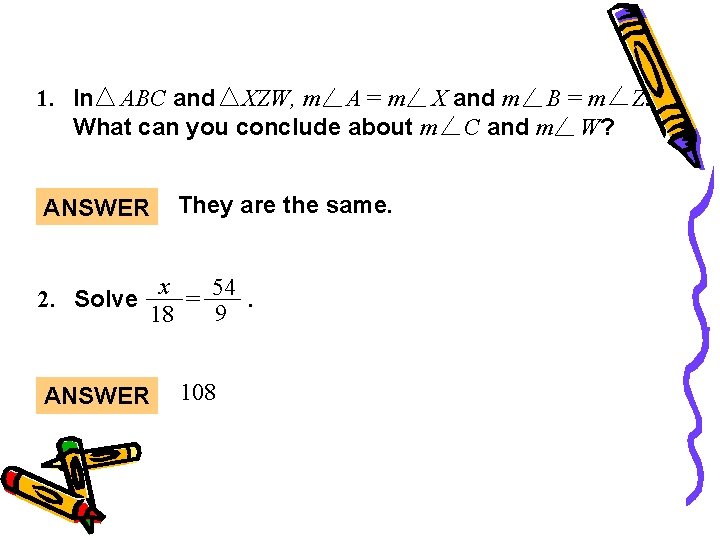
Warm-Up 1. In ABC and XZW, m A = m X and m B = m Z. What can you conclude about m C and m W? They are the same. ANSWER 2. Solve x = 54. 9 18 ANSWER 108

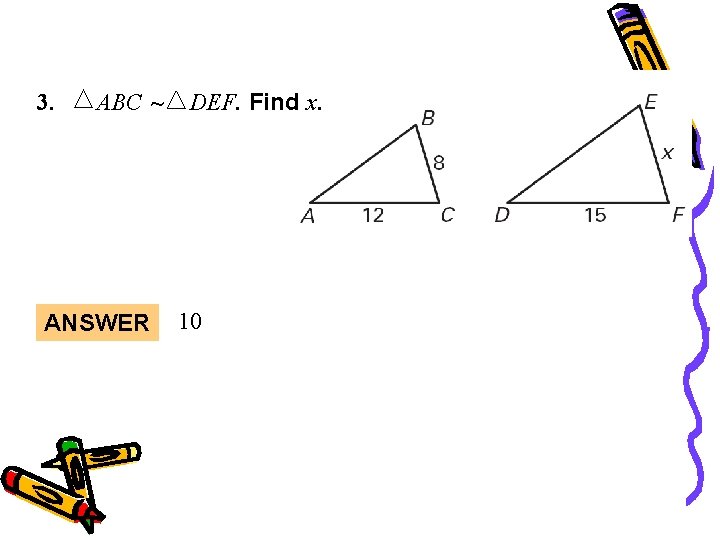
Warm-Up 3. ABC ~ ANSWER DEF. Find x. 10

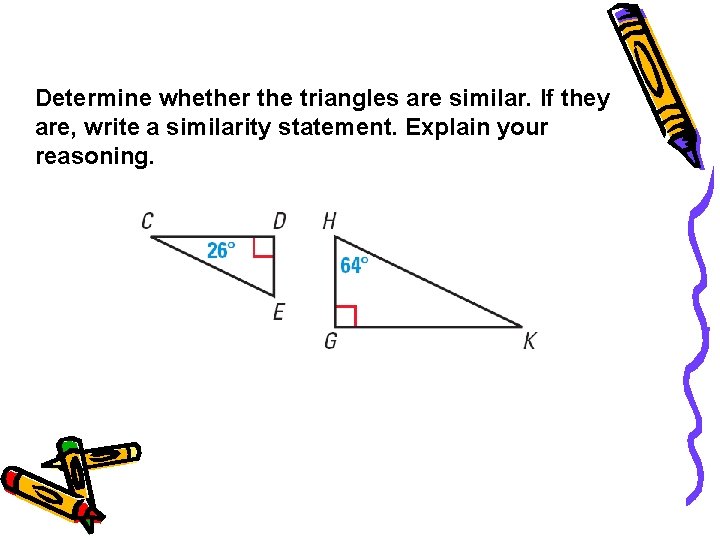
Example 1 Determine whether the triangles are similar. If they are, write a similarity statement. Explain your reasoning.

Example 1 SOLUTION Because they are both right angles, congruent. D and G are By the Triangle Sum Theorem, 26° + 90° + m E = 180°, so m E = 64°. Therefore, E and H are congruent. So, ∆CDE ~ ∆KGH by the AA Similarity Postulate.

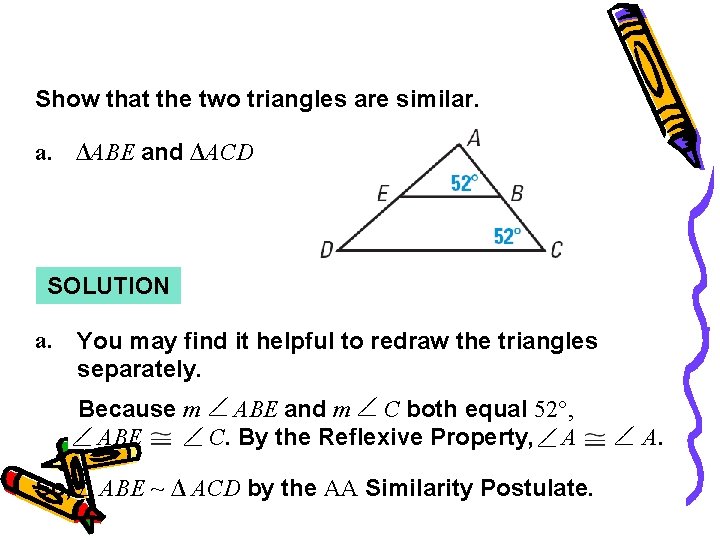
Example 2 Show that the two triangles are similar. a. ∆ABE and ∆ACD SOLUTION a. You may find it helpful to redraw the triangles separately. Because m ABE and m C both equal 52°, ABE C. By the Reflexive Property, A So, ∆ ABE ~ ∆ ACD by the AA Similarity Postulate. A.

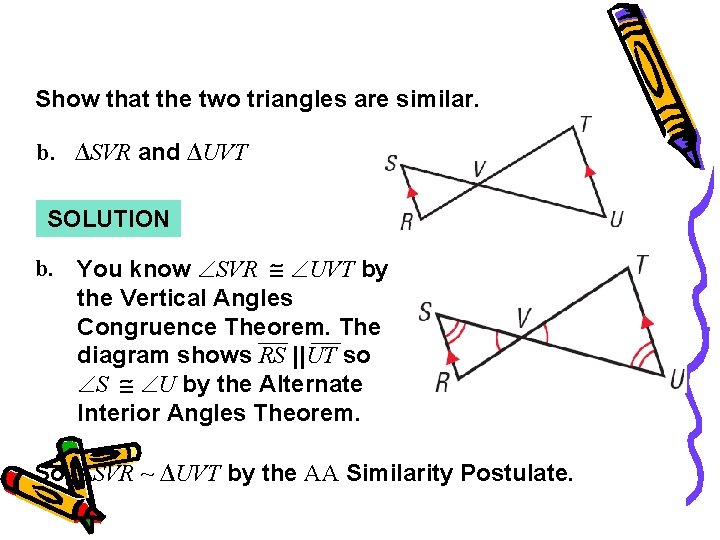
Example 2 Show that the two triangles are similar. b. ∆SVR and ∆UVT SOLUTION b. You know SVR UVT by the Vertical Angles Congruence Theorem. The diagram shows RS ||UT so S U by the Alternate Interior Angles Theorem. So, ∆SVR ~ ∆UVT by the AA Similarity Postulate.

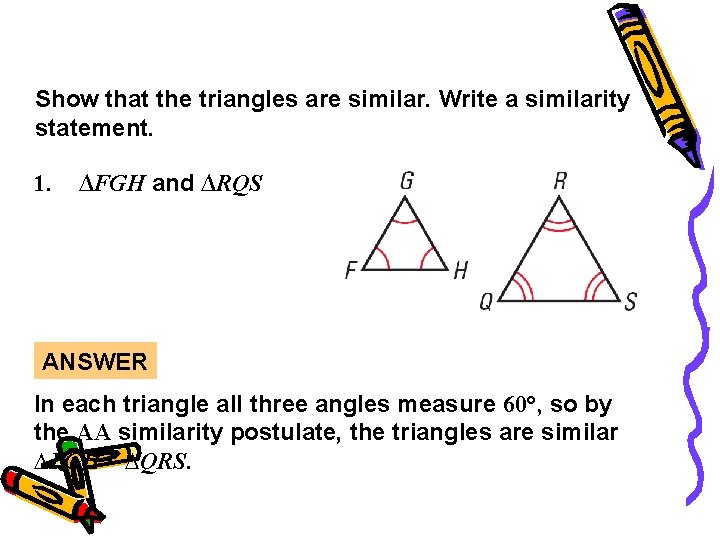
Guided Practice Show that the triangles are similar. Write a similarity statement. 1. ∆FGH and ∆RQS ANSWER In each triangle all three angles measure 60°, so by the AA similarity postulate, the triangles are similar ∆FGH ~ ∆QRS.

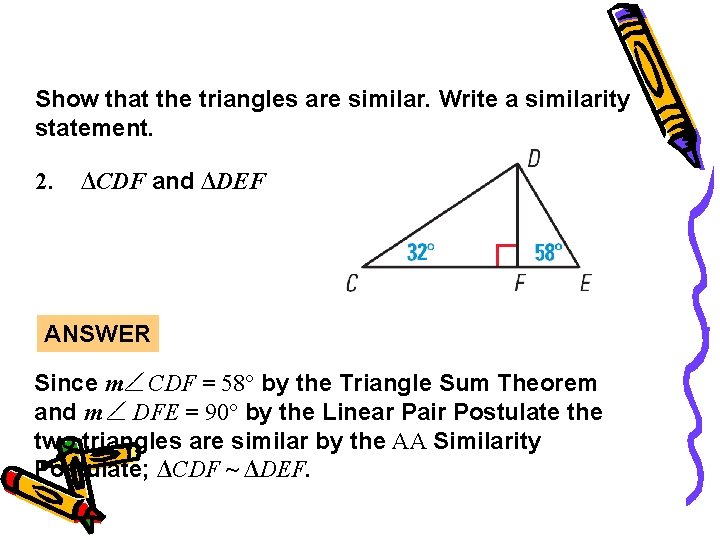
Guided Practice Show that the triangles are similar. Write a similarity statement. 2. ∆CDF and ∆DEF ANSWER Since m CDF = 58° by the Triangle Sum Theorem and m DFE = 90° by the Linear Pair Postulate the two triangles are similar by the AA Similarity Postulate; ∆CDF ~ ∆DEF.

Guided Practice 3. REASONING Suppose in Example 2, part (b), SR Could the triangles still be similar? Explain. ANSWER Yes; if S T, the triangles are similar by the AA Similarity Postulate. TU.

Example 3

Example 3 SOLUTION The flagpole and the woman form sides of two right triangles with the ground, as shown below. The sun’s rays hit the flagpole and the woman at the same angle. You have two pairs of congruent angles, so the triangles are similar by the AA Similarity Postulate.

Example 3 You can use a proportion to find the height x. Write 5 feet 4 inches as 64 inches so that you can form two ratios of feet to inches. 50 ft x ft = 40 in. 64 in. 40 x = 64(50) x = 80 Write proportion of side lengths. Cross Products Property Solve for x. ANSWER The flagpole is 80 feet tall. The correct answer is C.

Guided Practice 4. WHAT IF? A child who is 58 inches tall is standing next to the woman in Example 3. How long is the child’s shadow? ANSWER 36. 25 in.

Guided Practice 5. You are standing in your backyard, and you measure the lengths of the shadows cast by both you and a tree. Write a proportion showing how you could find the height of the tree. SAMPLE ANSWER tree height your height = length of shadow length of your shadow

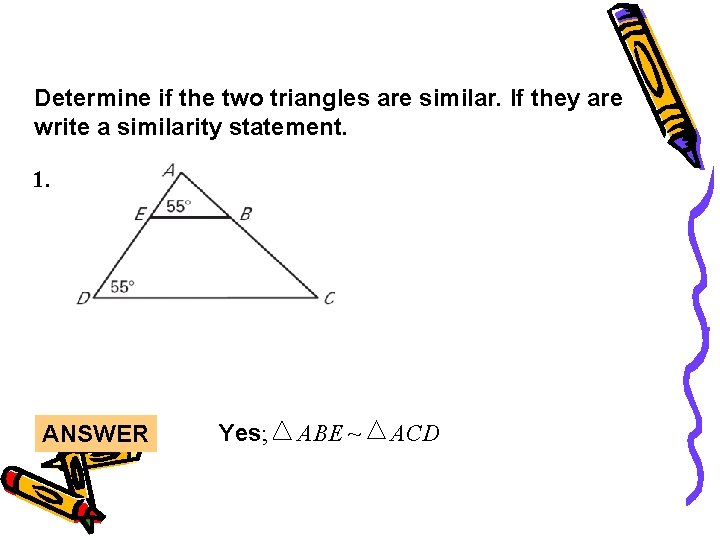
Lesson Quiz Determine if the two triangles are similar. If they are write a similarity statement. 1. ANSWER Yes; ABE ~ ACD

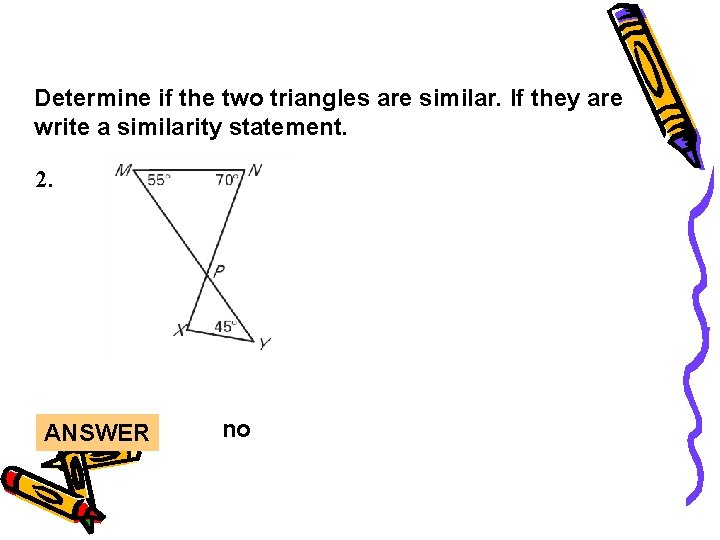
Lesson Quiz Determine if the two triangles are similar. If they are write a similarity statement. 2. ANSWER no

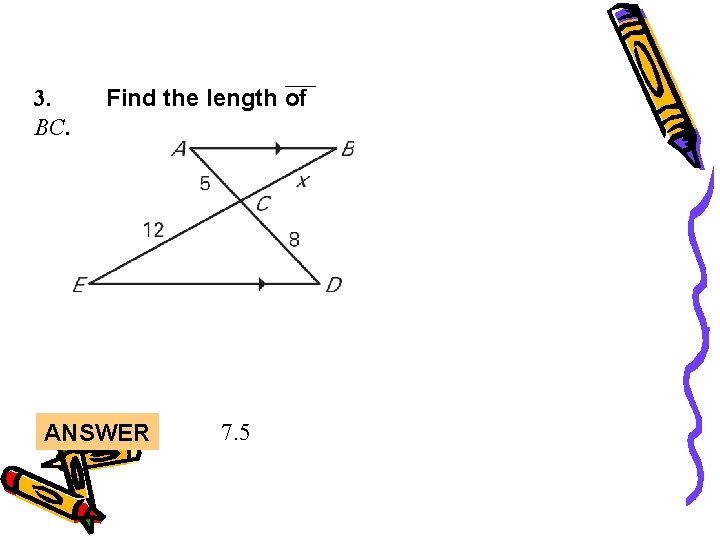
Lesson Quiz 3. BC. Find the length of ANSWER 7. 5

Lesson Quiz 4. A tree casts a shadow that is 30 feet long. At the same time a person standing nearby, who is five feet two inches tall, casts a shadow that is 50 inches long. How tall is the tree to the nearest foot? ANSWER 37 ft