GEOMETRY 3 CONGRUENCE OF TRIANGLE 3 1 Congruent

GEOMETRY 3. CONGRUENCE OF TRIANGLE.

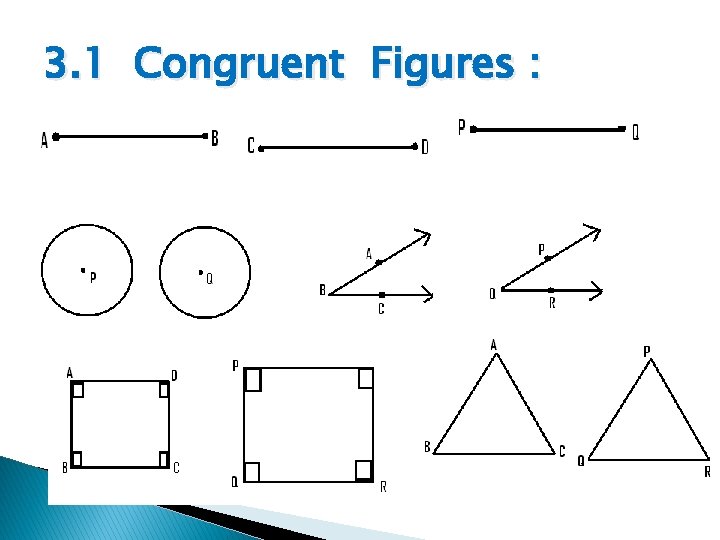
3. 1 Congruent Figures :

One to one corresponds & congruency of triangle � � � � � To determine whether the given two triangle are congruent i, e whether they have same shape & size. 1] Draw triangle ABC and triangle PQR of any shape and size on paper. 2] Cut this triangular pieces along the boundary. 3]Put one triangular piece over the other triangular piece & try to match them. 4]Try to find out all possible ways of keeping one triangular piece over other triangular piece. There are six different ways of putting one triangle over the other, among the two sets of vertices of triangles. � � 1] ∆ ABC ≅ ∆ PQR � 4] ∆ ABC≅ ∆ RQP 2] ∆ ABC ≅ ∆ QPR 5] ∆ ABC ≅ ∆ RQP 3] ∆ ABC ≅ ∆ QRP 6] ∆ ABC ≅ ∆ PRQ

� From this we understand that, out of this six correspondences, between the vertices of the triangles, if there exits at least one, in which the triangles cover each other exactly then we say the triangles are congruent with respect to that correspondence. � Definition : Out of six one to one correspondence between the vertices of two triangles, if there exist at-least one, one to one correspondence such that the sides and the angles of one triangle are congruent to the corresponding sides and angles of there triangles are said to be congruent with respect to that correspondence, and the property is known as congruence. Properties of Congruency in Triangles : � 1]Reflaxivity : ∆ABC≈∆ABC � 2]Symmetry : If ∆ABC ≈ ∆PQR then � ∆PQR ≈ ∆ABC � 3]Transitivity : If ∆ ABC≈∆PQR & ∆PQR ≈∆ XYZ then � ∆ ABC≈ ∆ XYZ. �

3. 5 Sufficient conditions for congruence of triangles : � in all six conditions are required to determine the congruency of the triangles. What are the least possible conditions to ensure the congruence of two triangles? � it can be seen that, three out of six conditions, if properly chosen are sufficient determine the congruency of the two triangles. when this tree conditions are satisfied, then the other tree automatically get satisfied, hence the triangles become congruent. This fact was first proved by ‘Euclid’ , the father of Geometry. � � Euclid of Alexandria was a Greek Mathematician known as ‘Father of Geometry. ’ His ‘Element’ is one of the most influence book in the history of Mathematics, serving as the main text book for teaching Geometry. Euclid also work on perspective, conic sections, spherical geometry and number theory.

3. 6] SAS test for congruency of triangles : � For a given correspondence, when two sides and included angle of one triangle are congruent to corresponding two sides and the included angle of the other triangle, then this two triangles are congruent. � 3. 7] Isosceles Triangle Theorem [the application � � SAS of test] 1] if two sides of triangles are congruent then the angle opposite to them are congruent. 2]If two angles of a triangle are congruent then the sides opposite them are congruent.

Isosceles triangle theorem : � If two sides of triangle are congruent then the angle opposite to them are congruent. Given : In ∆ PQR , seg PR ≅ seg PQ � To prove: ∠Q ≅ ∠R � Construction : Draw angle bisector of ∠QPR, which intersect � � � � side QR. Name the point of intersection as S. Proof : In ∆PQS & ∆ PRS seg PQ ≅ seg PR …. . . . [Given] ∠ QPS ≅ ∠RPS…………. [construction] seg PS ≅seg PS ………. [common side] ∴∆ PQS ≅ ∆PRS………. [SAS test] ∴ ∠Q ≅ ∠R ……………. [c. a. c. t]

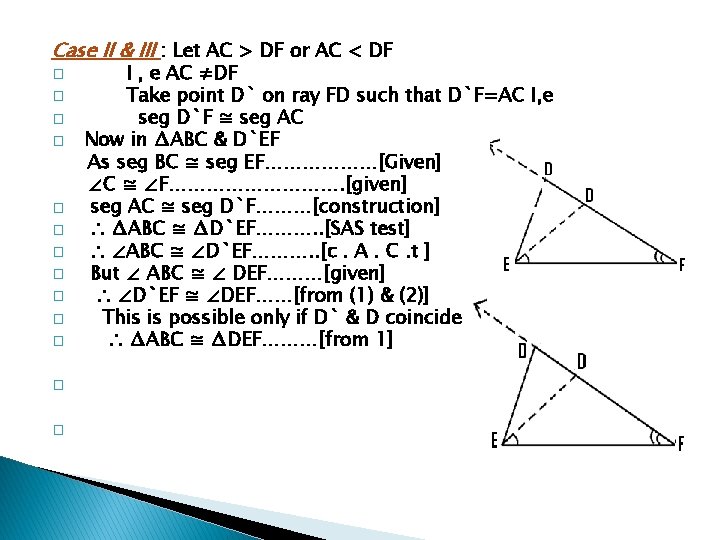
3. 8] A-S-A test for congruence of triangles � � � : For a given corresponds, when two angles & included side of one triangle are congruent to the corresponding to angles & the included side of the another triangle , then the two angles are congruent. Given: - In ∆ ABC & ∆ DEF ∠ABC ≅ ∠DEF, ∠ ACB ≅ ∠DEF , seg BC ≅ seg EF To prove: - ∆ ABC ≅ ∆ DE � Proof : - there are three possibilities regarding the seg AC & seg DF � � � 1]: - AC=DF ii] AC > DF iii] AC < DF CASE 1] : Let AC ≅ DF i , e seg AC ≅ DF & seg BC ≅seg………. [given] ∠C ≅ ∠F ………………………. . [given] ∴ ∆ ABC ≅ ∆DEF……………. . […………. . SAS Test]

Case II & III : Let AC > DF or AC < DF � � � � I , e AC ≠DF Take point D` on ray FD such that D`F=AC I, e seg D`F ≅ seg AC Now in ∆ABC & D`EF As seg BC ≅ seg EF………………[Given] ∠C ≅ ∠F……………. [given] seg AC ≅ seg D`F………[construction] ∴ ∆ABC ≅ ∆D`EF………. . [SAS test] ∴ ∠ABC ≅ ∠D`EF………. . [c. A. C. t ] But ∠ ABC ≅ ∠ DEF………[given] ∴ ∠D`EF ≅ ∠DEF……[from (1) & (2)] This is possible only if D` & D coincide ∴ ∆ABC ≅ ∆DEF………[from 1]

3. 9] SAA test for congruence of triangles for a given correspondence, when two angles & a non included side of one triangle are congruent to corresponding angles & the side of another triangle , then the two triangles are congruent. Given : In ∆ABC & ∆DEF ∠A≅ ∠D , ∠B ≅ ∠E , Seg BC ≅ seg EF prove that : ∆ ABC ≅ ∆ DEF Proof : In ∆ABC ∠A+ ∠B+ ∠C=180………[sum of the angles of triangle] In ∆DEF ∠D + ∠E+ ∠F= 180……. [sum of angles triangles] ∠A+ ∠B + ∠C= ∠D + ∠E+∠F…. [from (1) & (2)] but ∠A= ∠D & ∠B= ∠E ……. [given] ∴∠C= ∠F I, e ∠C=∠F Now consider ∆ABC and ∆DEF ∠B ≅ ∠E ……………. [Given] Seg BC ≅ seg EF………………[Given] ∠ C ≅ ∠F ……………. . [from iii] ∆ ABC ≅ ∆ DEF …………………[ASA test]

3. 10] SSS test for congruence of triangles For a given correspondence, when three sides of one triangle are congruent with three corresponding sides of another triangle then the two triangles are congruent. Given : In ∆ ABC & ∆ DEF seg AB ≅ seg DE, seg BC ≅ seg EF, and seg AC ≅ seg DF To prove : ∆ ABC ≅ ∆ DEF Construction: suppose seg BC is largest Side of ∆ABC , draw ∠PEF ≅ ∠ABC proof ; In ABC and PEF ∠ABC ≅ ∠PEF……. [construction] ∠ACB ≅ ∠ PFE……[construction] seg BC ≅ seg EF. . [Given] ∆ ABC ≅ ∆ PEF…. [ASA test]-(i) seg AB ≅ seg DE & seg AC ≅ seg PF. –(i) but seg AB ≅ seg DE & seg AC ≅ seg DF…. . [given]-(iii) Seg PE ≅ seg DE & seg PF ≅ seg DF …. . (iv) [from ii & iii]

Now in ∆DEP , seg PE ≅ seg DE………………… [from iv] ∠EDP ≅ ∠EPD……………. [v]…. . [Isosceles triangle theorem] Similarly in ∆ DEP ; Seg PF≅ seg DF……………. [from iv] ∠EDP ≅ ∠EPD ……………. [v]. [isosceles triangles theorem] I , e ∠FDP ≅ ∠ FPD…………. [vi] Adding [v] and [vi] We get ∠EDP+ ∠FDP= ∠EPD+ ∠FPD ∠EDF =∠ EPF…………………. [vii] Now in ∆ PEF & ∆DEF Seg PE ≅ seg DE…………. [from iv] Seg PF ≅ seg DF……………[from v] ∠EPF ≅ ∠EDF……………. . [from vii] ∆ PEF ≅ ∆ DEF……………. . [SAS test]……. . viii from [i] and [viii]we have, ∆ ABC ≅ ∆ DEF ………………[by transitivity]

3. 11] Hypotenuse – side theorem Two right angle triangle are congruent if the hypotenuse & a side of one triangle are congruent to the hypotenuse & corresponding side of the other triangle. Given : In ∆ABC & ∆PQR, � � � Hypotenuse AC ≅Hypotenuse PR Seg AB ≅seg PQ, ∠ABC= ∠PQR=90’ To prove : ∆ABC ≅∆PQR Construction : Take point S on ray RQ such that R-Q-S & seg BC ≅ seg QS.

Proof : In ∆ABC & ∆PQS Seg AB ≅seg PQ………. [Given] ∠ ABC ≅ ∠ PQS……………. . [each of 90’] Seg BC ≅ seg QS………. [construction] ∴ ∆ABC ≅∆ PQS………. . [SAS test] Seg AC ≅ seg PS……………. [c. S. c. t. ] But seg AC ≅ seg PR……. . [given] ∴ Seg PS ≅ seg PR…………. [ii] ∴ ∠R ≅ ∠S …………[Isosceles triangle theorem] Now In ∆PQR & ∆PQS ∠R ≅ ∠S ……………. . [from iii] ∠PQR ≅ ∠PQS…………. [Given] Seg PR ≅ seg PS………………. . [from ii] ∴ ∆PQR ≅ ∆PQS…………………. . [SAA test] ∴ ∆ABC ≅ ∆PQR …………………. . [from (i) & (ii)]

3. 14]Converse of an Isosceles triangle theorem If two angles of a triangle are congruent then the side opposite to them are congruent. Given : In ∆ABC ∠B ≅ ∠C � To prove : seg AB ≅ seg AC � Construction : Draw angle bisector of � � � � � ∠BAC which intersect side BC in point D. Proof : Consider ∆ABD & ∆ACD ∠BAD ≅ ∠CAD……………[construction] ∠B ≅ ∠ C…………. [Given] Seg AD ≅ seg AD ………………[common side] ∴ ∆ABD ≅ ∆ ACD…………………. [SAA test] Seg AB ≅ seg AC…………………[c. s. c. t. ] Hence sides opposite to congruent angle of triangle are congruent.

3. 15] In a right angle triangle the length of median drawn to the hypotenuse is half of the hypotenuse. Given : In ∆ABC , ∠ ABC=90’ Side AC is hypotenuse seg BD is median To prove : BD= ½ AC Construction : On ray BD take point E such that seg BD ≅ seg DE, draw seg EC Proof : In ∆ABD and ∆CED seg AD ≅seg CD………. . [Given] ∠ADB ≅ ∠CDE………………… [vertically opp. angle] Seg BD ≅seg ED…………………. [Construction] ∴ ∆ABD ≅ ∆CED………………. [SAS test] ∴seg AB ≅ seg CE………………. [c. s. c. t] And ∠BAD ≅ ∠ECD………………[c. a. c. t. ]

But these angles are alternate angles formed by transversal AC. ∴seg AB ‖ seg CE……………[Alternate angle test] � Now consider seg AB ‖ seg CE & transversal BC � ∠ABC and ∠ECB are interior angles. � ∴ ∠ABC+ ∠ECB=180’………………. . [interior angles] � But ∠ABC=90’……………. . [Given] � ∴ ∠ECB=90’ ………………[ii] � Now consider ∆ABC & ∆ECB � Seg AB ≅ seg EC ……………. [from i] � ∠ABC ≅ ∠ECB ………………[each is 90’ from (ii)] � Seg BC ≅ seg CB……………. . [common side] � ∴ ∆ABC ≅ ∆ECB……………[SAS test] � ∴seg AC ≅ seg BE, …………. [c. s. c. t. ] � i, e AC=BE � ∴½ AC = ½ BE………………[multiplying by ½] � But ½ BE=BD………………[Construction] � ∴BD= ½AC.

3. 16 Perpendicular Bisector of a Segment In this figure which line is the perpendicular l 1 l 2 bisector of seg AB and why ? l A B A 3 B Here , two conditions are imposed on the line. They are I. To be Perpendicular over the seg AB II. To be bisector of seg AB i. e. to pass through over the seg AB Using this criteria , let us define Perpendicular bisector � Definition : the line said to be a Perpendicular bisector of a given segment if it is Perpendicular to the segment and passes through its midpoint.

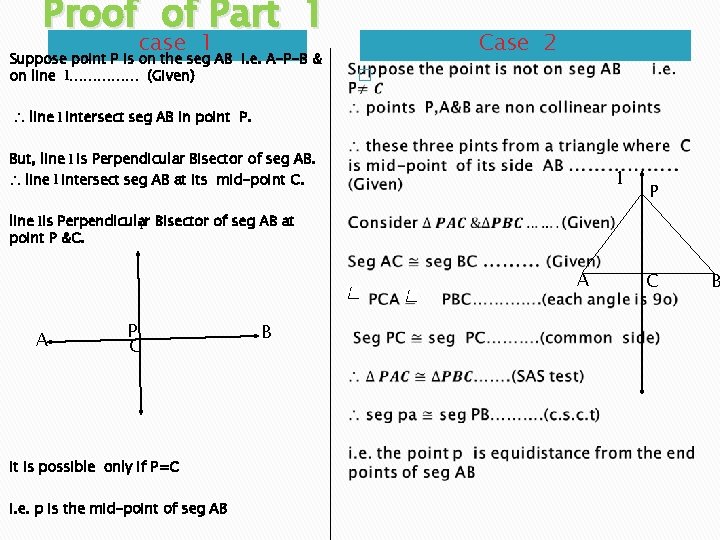
3. 17 Perpendicular Bisector theorem Part 1: if a point is on the Perpendicular Bisector of a given seg then it is equidistance from the end point of that seg Part 2: if a point is equidistance from the two points, then it lies on the Perpendicular Bisector of a seg joining the points. Proof of Part 1 Given: 1) line l is Perpendicular Bisector of seg AB. 2) Point P is on the line l 3) point C is the mid-point of seg AB. To prove: PA=PB Proof : Point P is on the line l ……………. (Given) there are two possibilities regarding point P 1)If may be seg AB i. e. A-PB or 2)If may not be on seg AB

Proof of Part 1 Case 2 case 1 Suppose point P is on the seg AB i. e. A-P-B & on line l…………… (Given) � ∴ line l intersect seg AB in point P. But, line l is Perpendicular Bisector of seg AB. ∴ line l intersect seg AB at its mid-point C. l P line lis Perpendicular l Bisector of seg AB at point P &C. A A P C It is possible only if P=C i. e. p is the mid-point of seg AB B C B

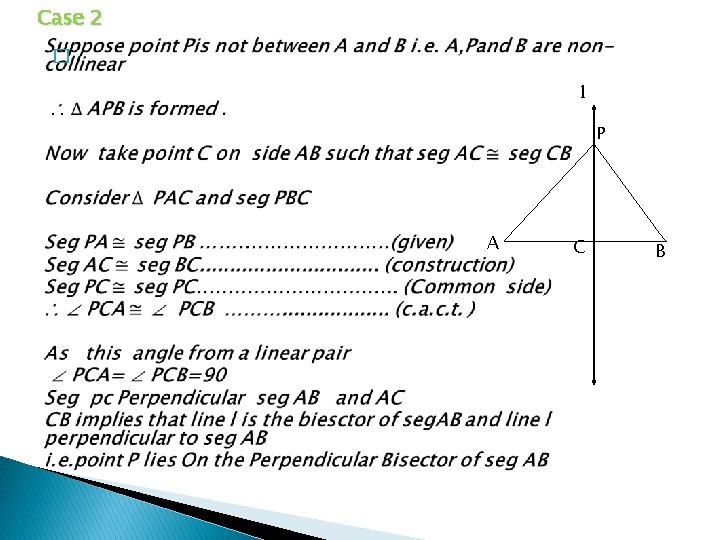
Proof of Part 2 �

Case 2 � l P A C B

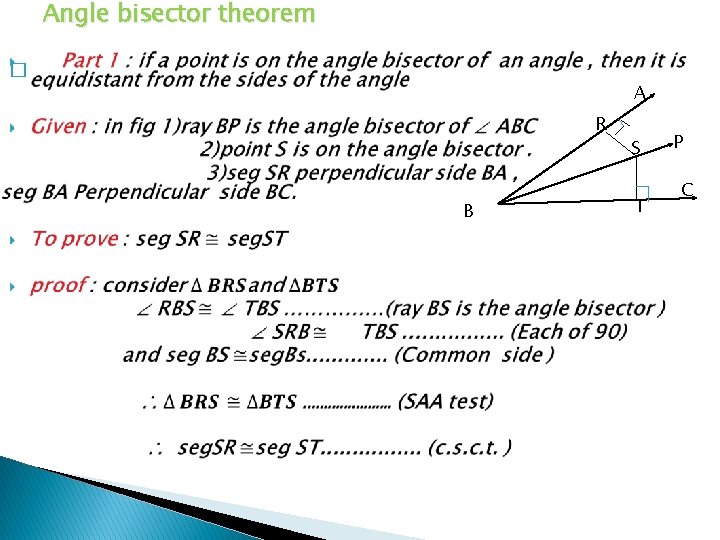
Angle bisector theorem � A R B S T P C

Part 2 �

locus � We have studied that theorems of perpendicular bisector and angle bisector. Do you remember condition is satisfied by the set of the point which lie on the perpendicular bisector of the segment ? Sudha replied : the point of equidistant from the points of that segment i. e. To equidistant from the end point of segment is the condition satisfied. � � Similarly think what condition is satisfied by the point of an angle bisector The set of point which satisfy certain condition is known as locus

Properties of triangle based on inequalities � P Q T R

� D E F A B C

� D A B C