Proving s are SSS SAS HL ASA AAS

Proving Δs are : SSS, SAS, HL, ASA, AAS, & CPCTC

SSS Side-Side Postulate • If 3 sides of one Δ are to 3 sides of another Δ, then the Δs are .

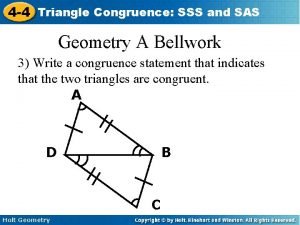
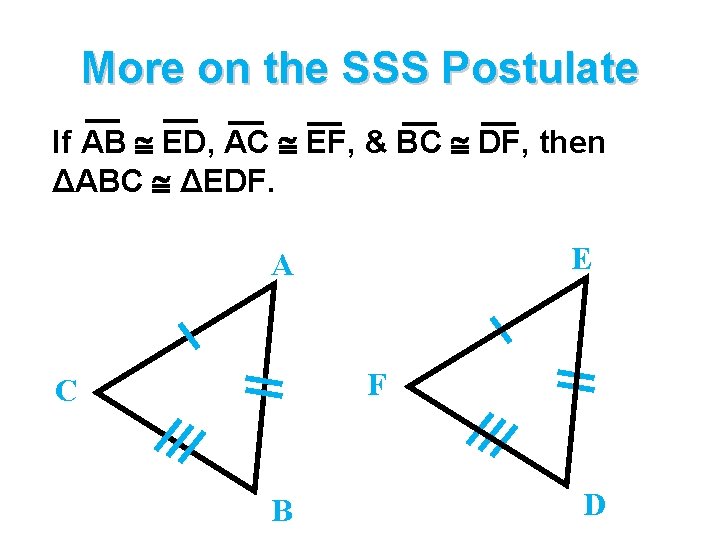
More on the SSS Postulate If AB ED, AC EF, & BC DF, then ΔABC ΔEDF. E A F C B D

EXAMPLE 1: Use the SSS Congruence Postulate Write a proof. GIVEN PROVE Proof KL NL, KM KLM NM NLM It is given that KL NL and KM By the Reflexive Property, LM So, by the SSS Congruence Postulate, KLM NM LN.

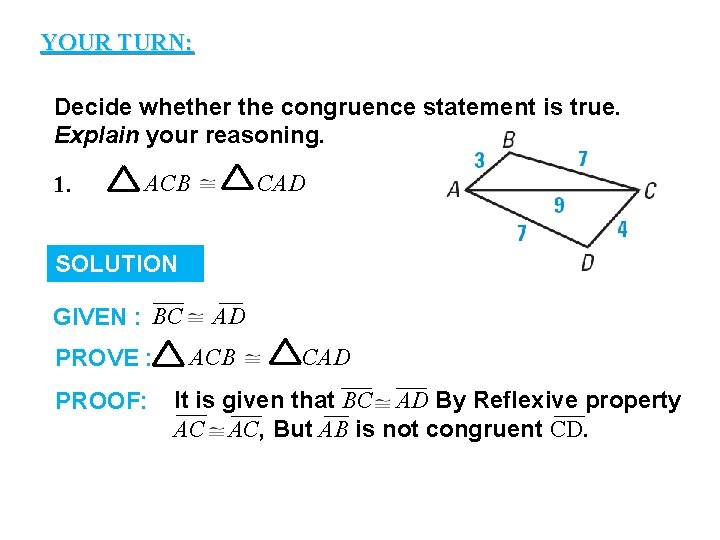
YOUR TURN: GUIDED PRACTICE Decide whether the congruence statement is true. Explain your reasoning. 1. ACB CAD SOLUTION GIVEN : BC PROVE : PROOF: AD ACB CAD It is given that BC AD By Reflexive property AC AC, But AB is not congruent CD.

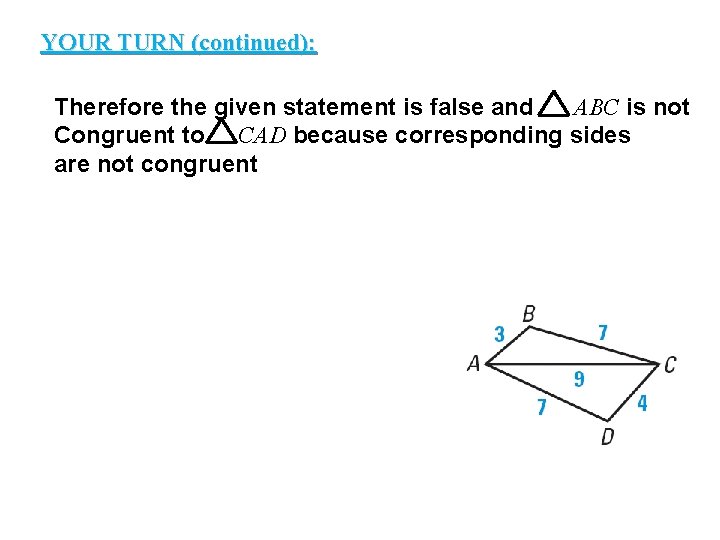
YOUR TURN (continued): GUIDED PRACTICE Therefore the given statement is false and ABC is not Congruent to CAD because corresponding sides are not congruent 1.

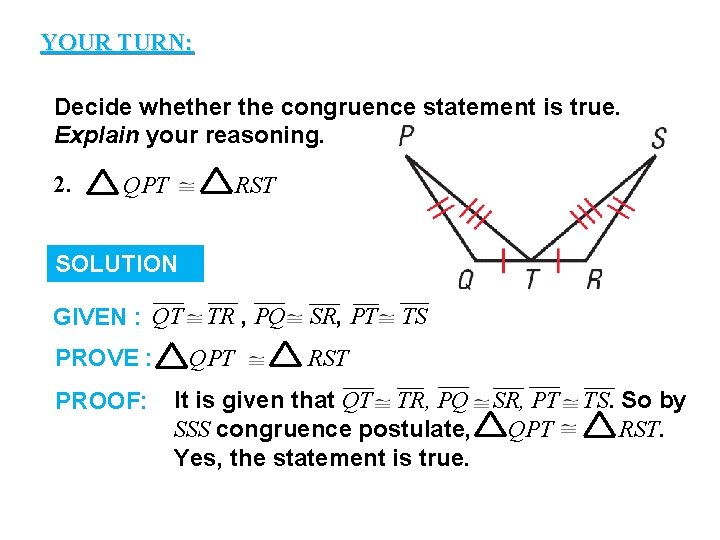
YOUR TURN: GUIDED PRACTICE Decide whether the congruence statement is true. Explain your reasoning. 2. QPT RST SOLUTION GIVEN : QT PROVE : PROOF: TR , PQ QPT SR, PT TS RST It is given that QT TR, PQ SR, PT SSS congruence postulate, QPT Yes, the statement is true. TS. So by RST.

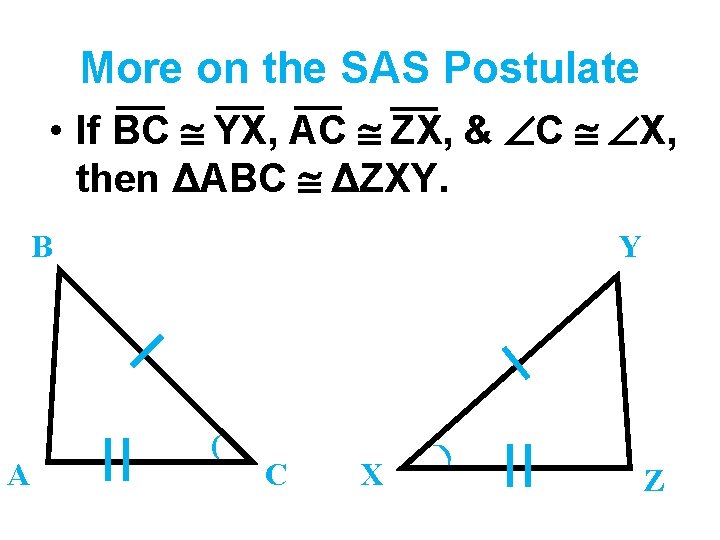
SAS Side-Angle-Side Postulate • If 2 sides and the included of one Δ are to 2 sides and the included of another Δ, then the 2 Δs are .

More on the SAS Postulate • If BC YX, AC ZX, & C X, then ΔABC ΔZXY. B A Y ( C X ) Z

EXAMPLE Example 2: 2 Use the SAS Congruence Postulate Write a proof. GIVEN BC DA, BC AD ABC PROVE CDA STATEMENTS S REASONS 1. BC DA 1. Given 2. BC AD 2. Given A 3. S 4. BCA AC DAC CA 3. Alternate Interior Angles Theorem 4. Reflexive Property of Congruence

EXAMPLE Example 22(continued): STATEMENTS 5. ABC CDA REASONS 5. SAS Congruence Postulate

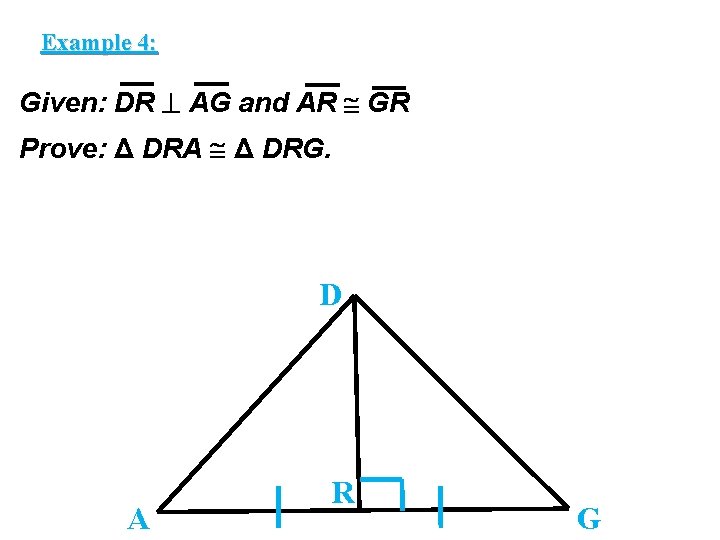
Example 4: Given: DR AG and AR GR Prove: Δ DRA Δ DRG. D A R G

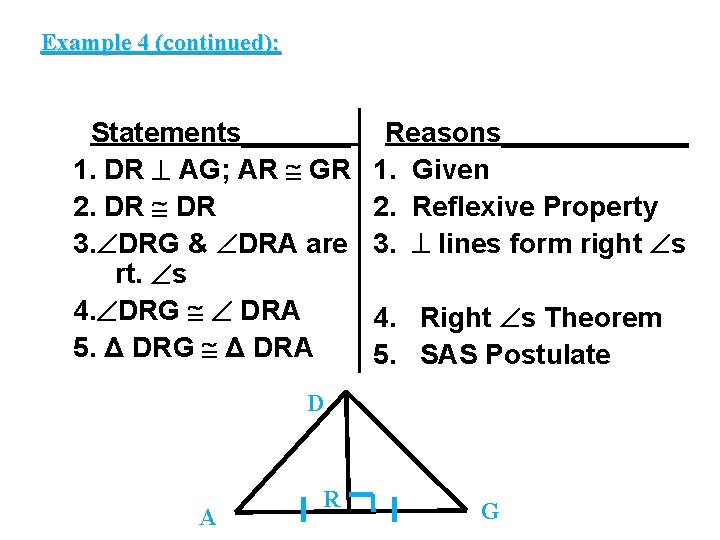
Example 4 (continued): Statements_______ 1. DR AG; AR GR 2. DR 3. DRG & DRA are rt. s 4. DRG DRA 5. Δ DRG Δ DRA Reasons______ 1. Given 2. Reflexive Property 3. lines form right s 4. Right s Theorem 5. SAS Postulate D A R G

HL Hypotenuse - Leg Theorem • If the hypotenuse and a leg of a right Δ are to the hypotenuse and a leg of a second Δ, then the 2 Δs are .

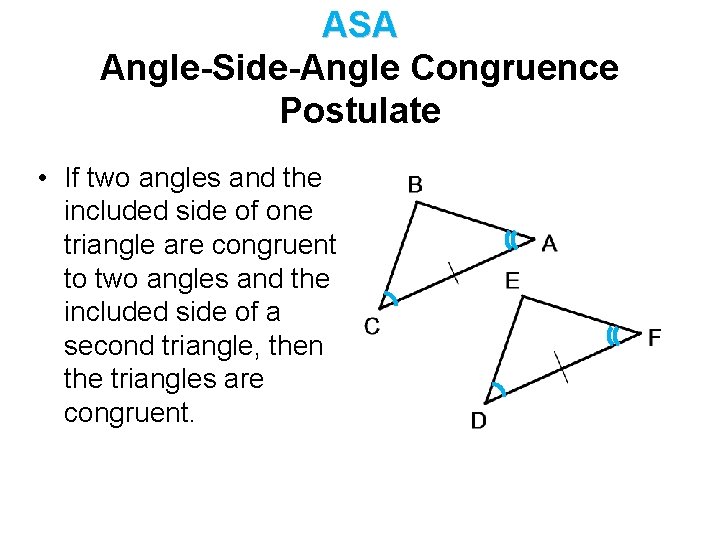
ASA Angle-Side-Angle Congruence Postulate • If two angles and the included side of one triangle are congruent to two angles and the included side of a second triangle, then the triangles are congruent.

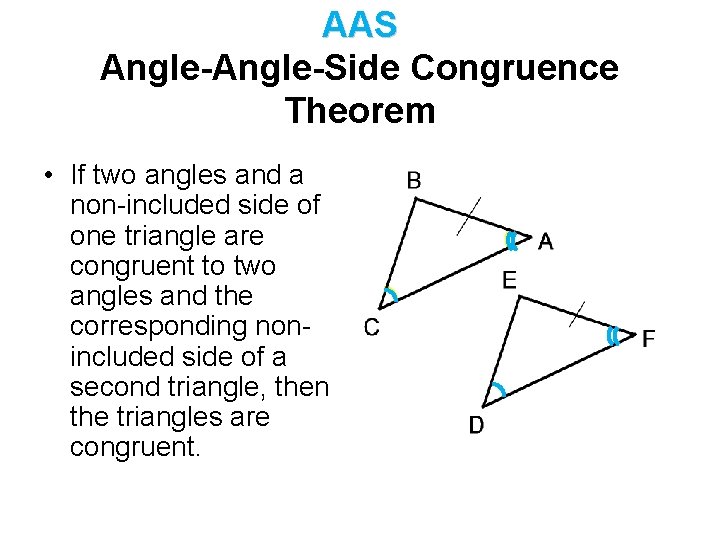
AAS Angle-Side Congruence Theorem • If two angles and a non-included side of one triangle are congruent to two angles and the corresponding nonincluded side of a second triangle, then the triangles are congruent.

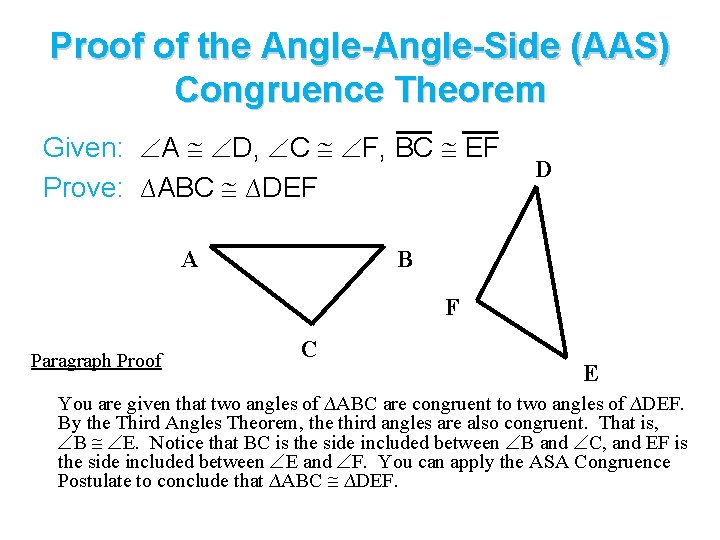
Proof of the Angle-Side (AAS) Congruence Theorem Given: A D, C F, BC EF Prove: ∆ABC ∆DEF A D B F Paragraph Proof C E You are given that two angles of ∆ABC are congruent to two angles of ∆DEF. By the Third Angles Theorem, the third angles are also congruent. That is, B E. Notice that BC is the side included between B and C, and EF is the side included between E and F. You can apply the ASA Congruence Postulate to conclude that ∆ABC ∆DEF.

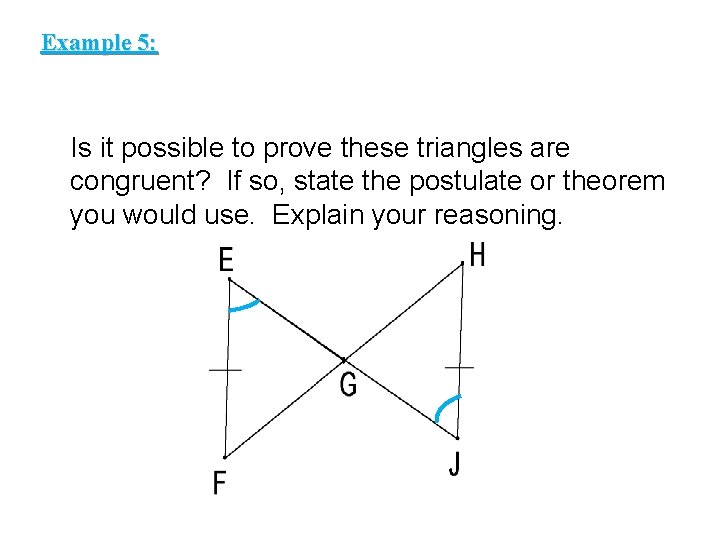
Example 5: Is it possible to prove these triangles are congruent? If so, state the postulate or theorem you would use. Explain your reasoning.

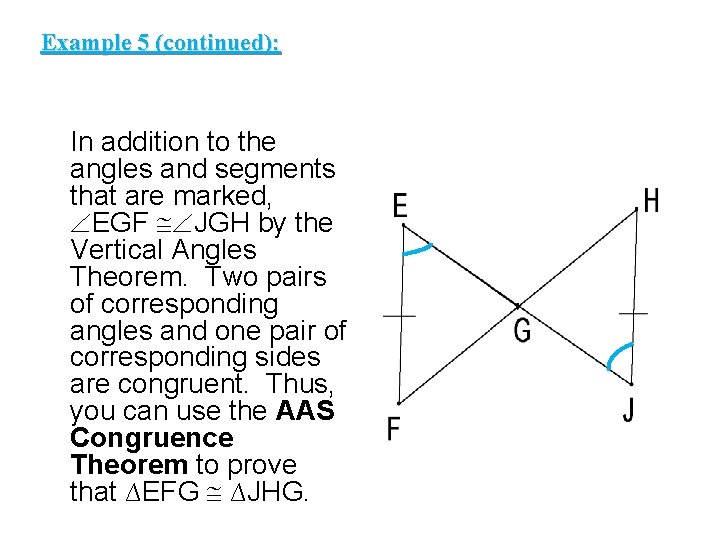
Example 5 (continued): In addition to the angles and segments that are marked, EGF JGH by the Vertical Angles Theorem. Two pairs of corresponding angles and one pair of corresponding sides are congruent. Thus, you can use the AAS Congruence Theorem to prove that ∆EFG ∆JHG.

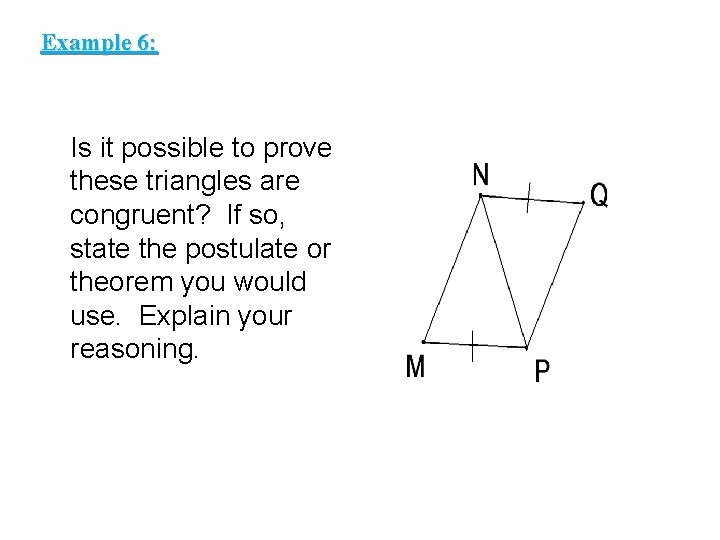
Example 6: Is it possible to prove these triangles are congruent? If so, state the postulate or theorem you would use. Explain your reasoning.

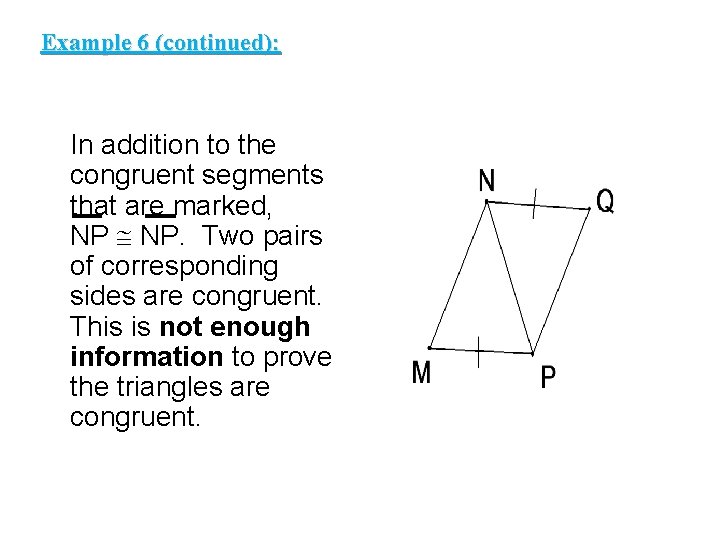
Example 6 (continued): In addition to the congruent segments that are marked, NP NP. Two pairs of corresponding sides are congruent. This is not enough information to prove the triangles are congruent.

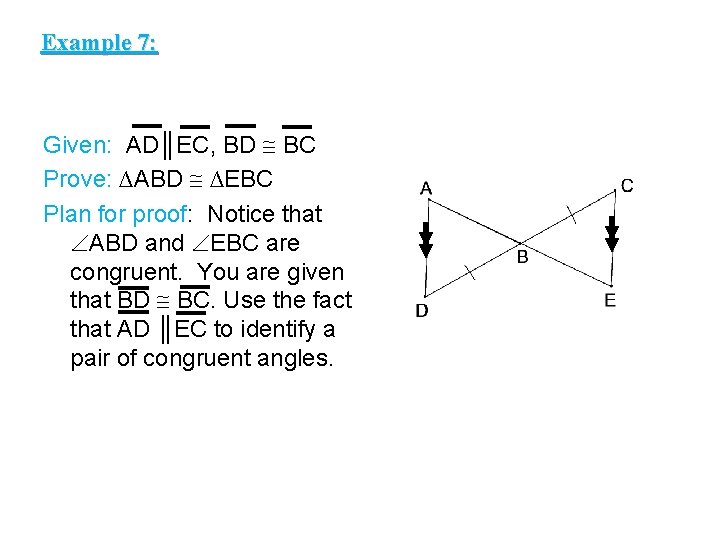
Example 7: Given: AD║EC, BD BC Prove: ∆ABD ∆EBC Plan for proof: Notice that ABD and EBC are congruent. You are given that BD BC. Use the fact that AD ║EC to identify a pair of congruent angles.

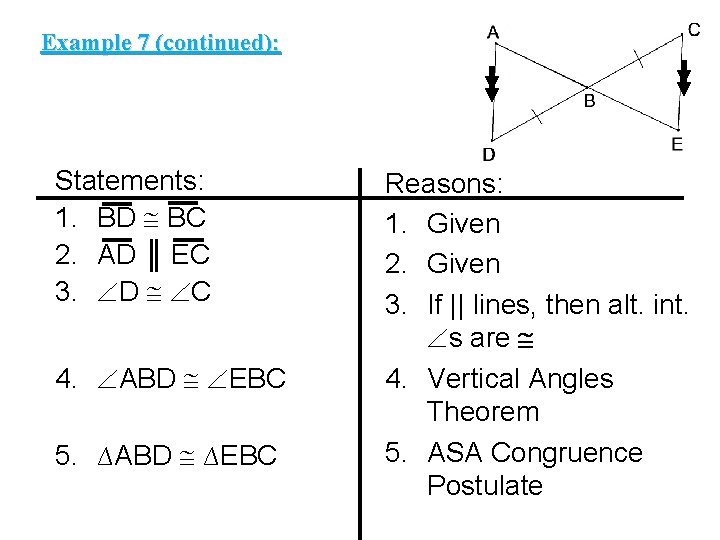
Example 7 (continued): Statements: 1. BD BC 2. AD ║ EC 3. D C 4. ABD EBC 5. ∆ABD ∆EBC Reasons: 1. Given 2. Given 3. If || lines, then alt. int. s are 4. Vertical Angles Theorem 5. ASA Congruence Postulate

CPCTC

CPCTC Given: Prove: D B STATEMENTS REASONS