Logique et raisonnement scientifique cours transversal Collge Doctoral

Logique et raisonnement scientifique cours transversal Collège Doctoral Pr. Alain Lecomte

1. Un sommaire et quelques idées de la logique argumentation à la logique des processus

l Qu’est-ce que la logique? – – – Un truc de philosophe? Un truc de matheux? La science du raisonnement? l – l L’étude du « vrai » ? Une idée : les discours – – l oui… lequel? Évaluer leur cohérence L’argumentation, le dialogue Quels discours? – – Les mathématiques Frege : « Après que la mathématique se fut pour un temps écartée de la rigueur euclidienne, elle y revient, et non sans de vifs efforts pour la dépasser » (Les Fondements de l’Arithmétique)

suite l C’est tout? Seulement les mathématiques? – – Déjà beaucoup… Et puis non, pas seulement les mathématiques l Les mathématiques comme « laboratoire »

suite l Une vieille histoire – – – Une vieille histoire (1) : Aristote, logique antique et logique médiévale, la disputatio, l’argument de Saint-Anselme, « fallacies » , des logiques exotiques Une vieille histoire (2) : Kant, Husserl, Cavaillès, Wittgenstein Une vieille histoire (3): la rencontre avec les mathématiques, Cantor, Dedekind, Frege

suite l La crise des fondements et le « programme de Hilbert » – Comment peut-on être sûr qu’une théorie est correcte? Qu’elle est « vraie » ? l – Peut-on définir le « vrai » ? l – En refaisant tous ses raisonnements avec des moyens dont on est sûr : idée de Hilbert Le concept de vérité dans les langages formalisés : Tarski théorie des modèles, langue / métalangue Peut-on démontrer tout ce qui est « vrai » ? l Théorèmes d’incomplétude : Gödel

suite l Le rôle de l’intuitionnisme – – – Une réaction contre le formalisme : Brouwer Une présentation de la logique intuitionniste (Heyting) Qu’est-ce qu’elle apporte? l l Quelques surprises: interprétation de Kripke Comment le savoir croît…

Le rôle de l’intuitionnisme l « doutes sur le tiers exclu » Brouwer, 1908 – – « La fonction des principes logiques n’est pas de diriger les raisonnements mathématiques appliqués à des réalités empiriques, mais de décrire, dans le langage des raisonnements, les régularités qui ont été obéies. Si on s’exprime en langage en suivant ces régularités, et en perdant le contact des systèmes mathématiques, on court le risque de paradoxes tels que l’Epiménide » .

Le rôle de l’intuitionnisme-2 l l l Syllogisme : non contestable (simple idée d’emboîtement de systèmes) Contradiction : idem ( « l’effectuation de l’emboîtement d’un système a dans un système b d’une façon déterminée, et vle fait de se heurter à l’impossibilité de cet emboîtement, sont mutuellement incompatibles » Tiers exclu : ?

Interrogation sur les concepts fondamentaux l Faut-il modifier la logique? – – – « Si A alors B » … une pure question d’arrangement de valeurs de vérité, Une « implication stricte » ? (Lewis) Vers les logiques modales

Logiques modales l Vous avez dit « modale » ? – – Le nécessaire et le possible L’obligatoire et le permis Le futur et le passé Savoir et croire l – Quel sens attribuer à un énoncé de croyance? Comment modéliser le temps à l’intérieur d’une logique?

où la machine intervient l Le problème de la décision, la logique et la machine – l Introduction d’une nouvelle problématique en logique : Turing, Church A. Church: Le lambda-calcul et nos retrouvailles avec l’intuitionnisme

Un autre problème posé par Hilbert: l’Entscheidungsproblem Le problème de la décision est résolu si l’on connaît une procédure qui permette de déterminer, en utilisant un nombre fini d’opérations, la validité, respectivement la satisfaisabilité d’une expression logique donnée (1928)

Turing (1936) l l l Machines de Turing Machine de Turing universelle Indécidabilité du problème de l’arrêt

Le -calcul de Church 1934? - 1936 l formuler avec précision le problème de la substitution des variables dans une expression qui représente une fonction – – l l l Application Abstraction Équivalence avec Md. T Théorème de Church-Rosser Une condition pour la normalisation : termes « typés »

Où cela rencontre l’intuitionnisme l l l Système de typage = logique intuitionniste Application = modus ponens Abstraction = introduction de La logique intuitionniste a un contenu algorithmique Prouver c’est programmer!

l Pourquoi la logique est utile: – – l Prouver c’est programmer Prouver c’est planifier La logique et les sciences modernes – La logique comme science des processus informationnels convergents : l langue, biologie, cognition

Prouver c’est planifier l l l cf. une action produit un changement dans le monde utilise des ressources se réalise par combinaison d’actions plus élémentaires

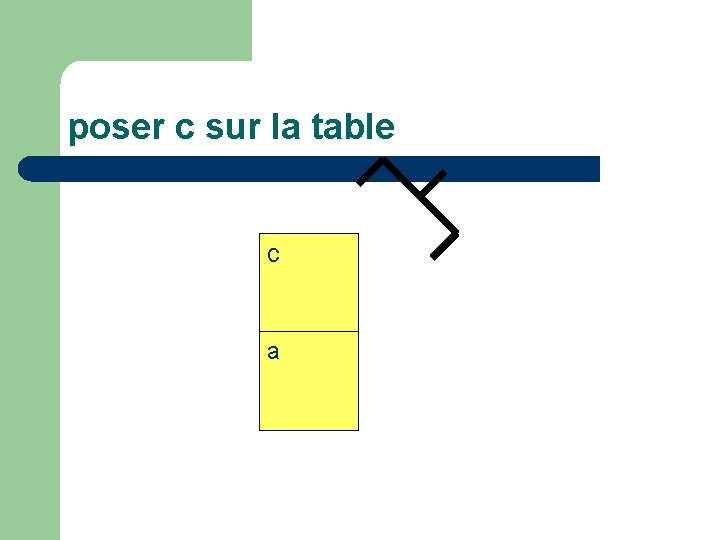
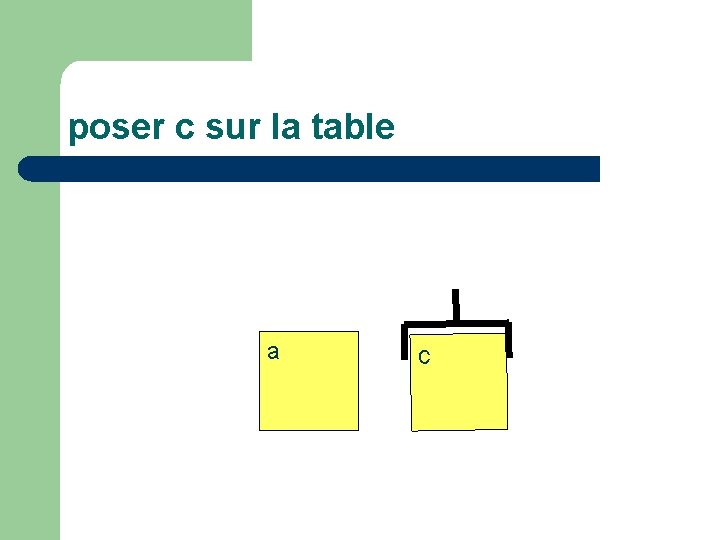
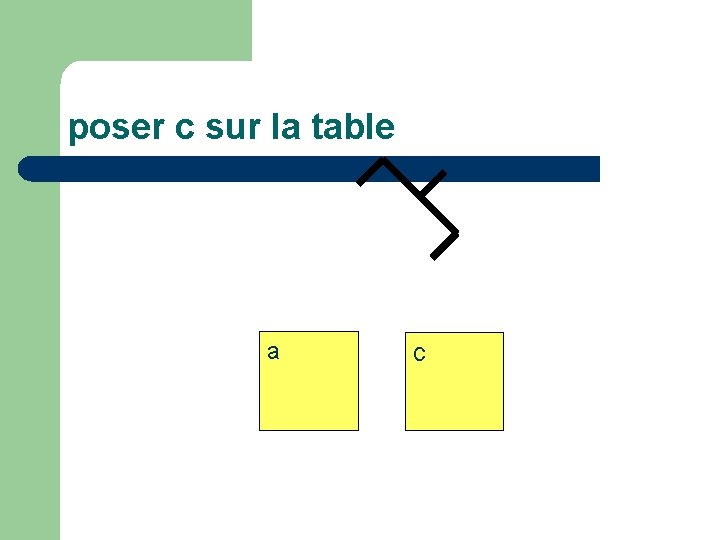
poser c sur la table c a

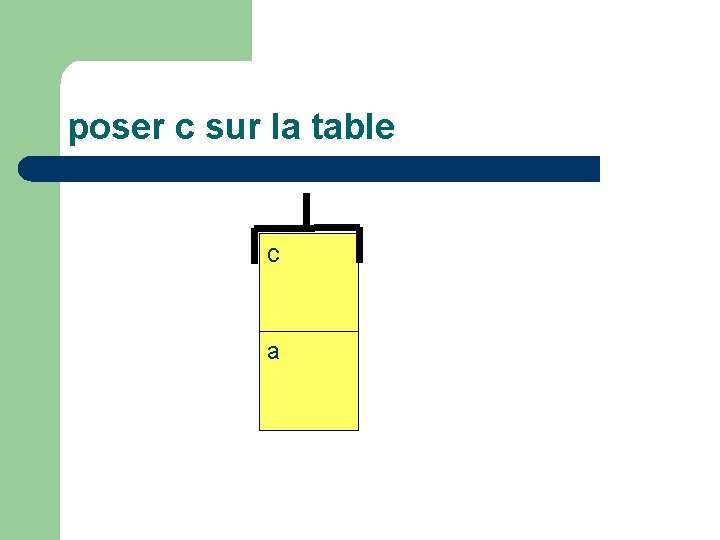
poser c sur la table c a

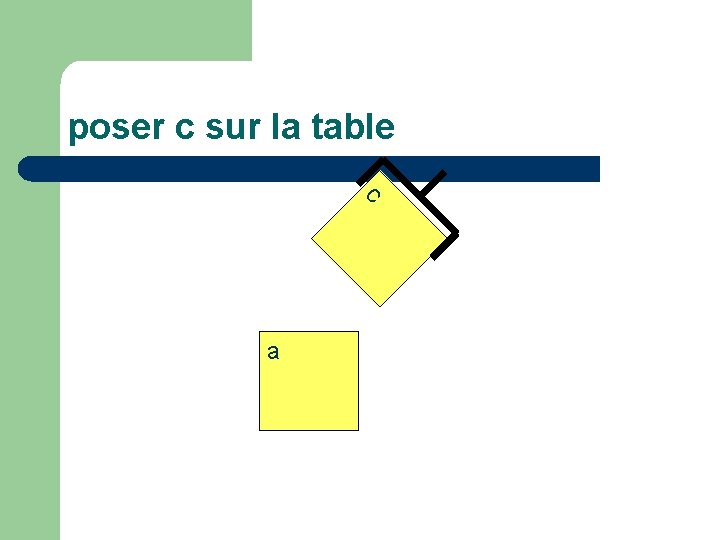
poser c sur la table c a

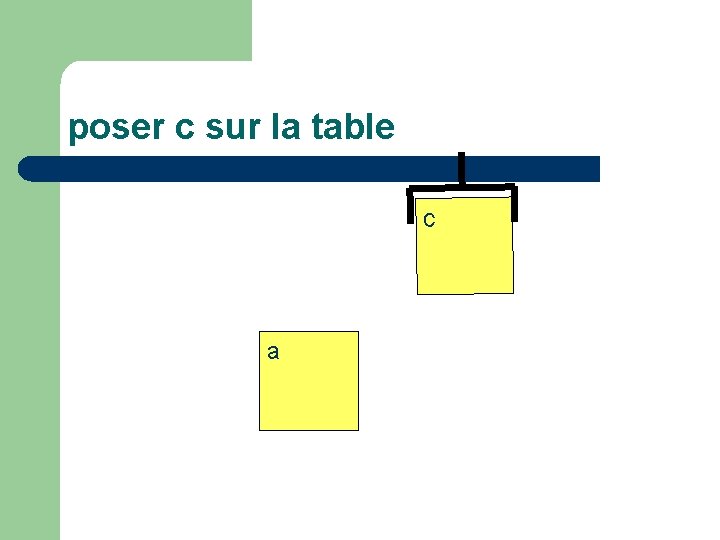
poser c sur la table c a

poser c sur la table a c

poser c sur la table a c

Passer de l’état du monde: l main vide (V) l c en haut de pile (donc accessible) (H(c)) l c sur a (S(c, a)) à l main vide l c en haut de pile l c en bas de pile (B(c)) l a en haut de pile

décrit par le séquent : V, H(c), S(c, a) V H(c) B(c) H(a)

Actions élémentaires l l prendre(x) : poser(x) : oter(x, y) : mettre(x, y) : V, H(x), B(x) T(x) V H(x) B(x) V, H(x), S(x, y) T(x) H(y) T(x), H(y) V H(x) S(x, y)

preuve poser(c) H(a) ------------------- - droite T(c), H(a) V H(c) B(c) H(a) ------------------ - gauche oter(c, a) T(c) H(a) V H(c) B(c) H(a) ------------------------------------------coupure V, H(c), S(c, a) V H(c) B(c) H(a)

preuve action? l l On peut extraire une composition d’actions d’une preuve comme on peut extraire un programme d’une preuve (informatique théorique)

biologie l Antoine Danchin: « la cellule est un ordinateur vivant » – – – Physique : matière, énergie, temps… Biologie : Physique + information, codage, contrôle… Arithmétique : chaînes d’entiers, récursivité, codage… Informatique : arithmétique + programme + machine… » « comme dans le cas de la construction d’une machine, dans celui de la construction d’une cellule, on a besoin d’un livre de recettes… cela demande ensuite qu’on soit capable de changer le texte de la recette en quelque chose de concret : ceci consiste dans le « transfert d’information » . Dans une cellule, ce transfert d’information est assuré par le programme génétique »

interaction & : choix « actif » (vous avez le choix entre … et …) : choix « passif » (l’un ou l’autre, vous ne décidez pas) : les deux, dans un ordre séquentiel non déterminé : les deux, en parallèle, par exemple l’échange (l’un contre l’autre) : le changement de point de vue

interprétation l l l Interaction la logique n’est plus seulement interprétable comme « décrivant un extérieur » , elle s’interprète « par rapport à elle-même » , autrement dit elle réfère à ses propres procédures (elles se répondent entre elles)

Un aspect… ludique? l Retour sur le dialogue et l’argumentation: – – – Logique dialogique « Game Theoretical Semantics » et IF-logique (Hintikka, Sandu…) Interprétation de la logique linéaire

2. Retour sur une vieille histoire d’Aristote à Hilbert

Qu’est-ce que la logique? l Hilary PUTNAM, 1971: (1 ) tous les S sont M tous les M sont P (donc) tous les S sont P (2) x est identique à x (3) non (p et (non p)) (4) p ou (non p)

l …. Tout ceci, même s'ils ne sont pas d'accord sur l'exposition des principes respectifs à l'œuvre dans ces différents cas. Il existe donc bien un corpus de "doctrine permanente " en logique

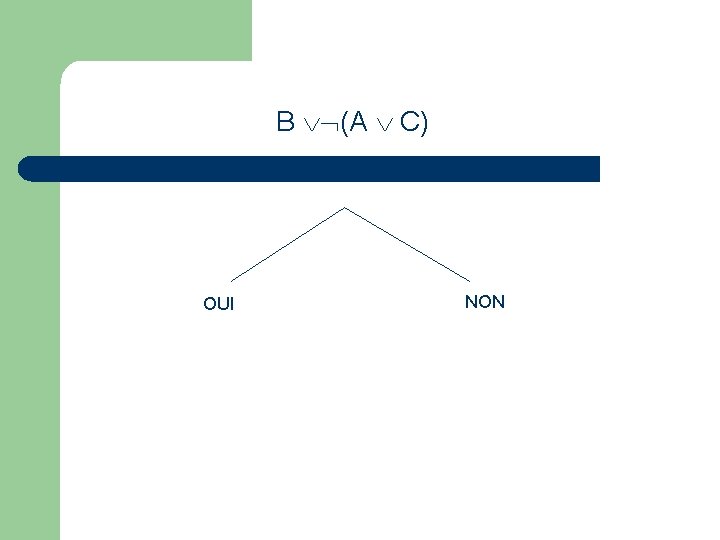
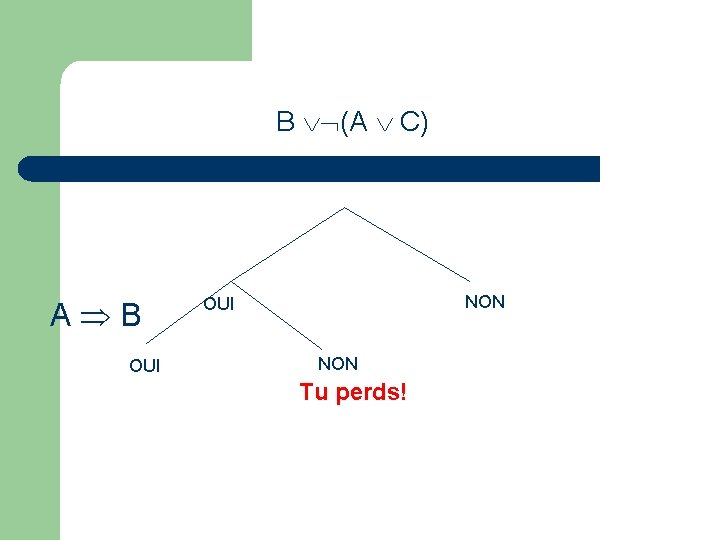
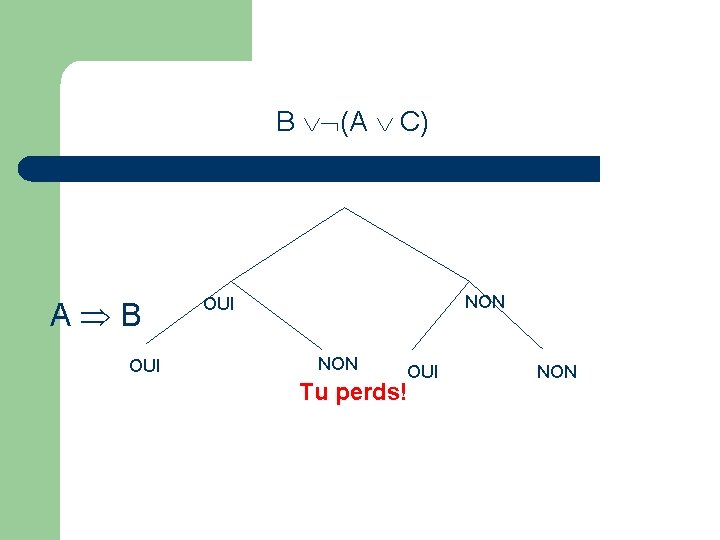
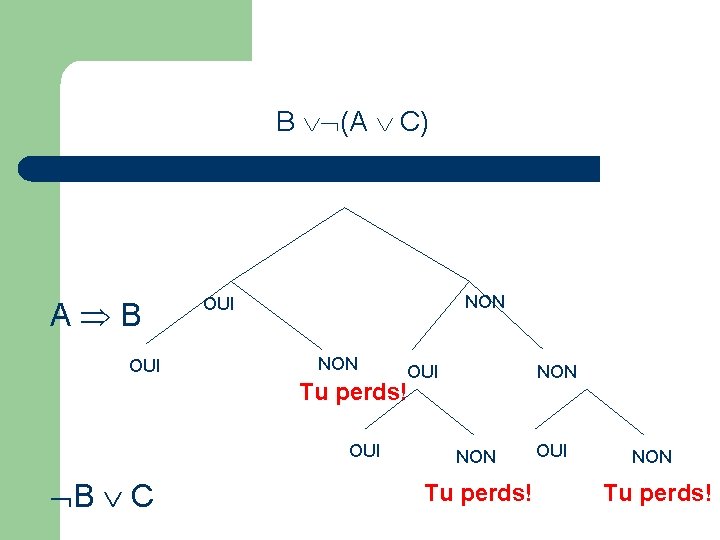
Maintenir la cohérence du discours l l Jeu de l’obligatio: (1) B (A C) (2) A B (3) B C

B (A C) OUI NON

B (A C) A B OUI NON Tu perds!

B (A C) A B OUI NON OUI Tu perds! NON

B (A C) A B OUI NON Tu perds! OUI B C NON Tu perds! OUI NON Tu perds!

Aristote l l l Théorie du syllogisme 1ère figure : BARBARA, CELARENT, DARII, FERIO 2ème figure : CESARE, CAMESTRES, FESTINO, BAROCO 3ème figure : DARAPTI, FELAPTON, DISAMIS, DATISI, BOCARDO, FERISON 4ème figure : BAMALIP, CALEMES, DIMATIS, FESAPO, FRESION

Le syllogisme aristotélicien l l l Tous les hommes sont mortels Socrate est un homme Donc Socrate est mortel – – – moyen : homme majeur : mortel mineur : Socrate

… ah! Barbara, comme il pleuvait fort sur Brest ce jour là… l l l l B A Tout M est S (universelle affirmative) R B A Tout X est M (universelle affirmative) R A Tout X est S (universelle affirmative) NB : le moyen est sujet de la majeure et prédicat de la mineure

celarent l l l l C E L A R E N T Aucun M n’est S (universelle négative) Tout X est M (universelle affirmative) Aucun X n’est S (universelle négative)

Logique indienne (à partir du 2ème siècle) l l l Proposition : il y a du feu sur la montagne Raison : parce qu’il y a de la fumée sur la montagne Exemple : comme dans une cuisine, et pas sur un lac Application : il en est ainsi Conclusion : donc il y a du feu

« fallacies » catalogue de formes d’argumentation fausses – affirmation du conséquent l – accident l – En général les oiseaux volent, Tweety le Pingouin est un oiseau, donc Tweety vole pétition de principe l – Si p alors q, q, donc p L’âme est immortelle parce qu’elle ne meurt jamais etc. ref: Hamblin, « Fallacies » , 1970

L’argument ontologique l l [l’] insensé <celui qui dit que Dieu n’est pas>, quand il entend cela même que je dis : "quelque chose de tel que rien ne se peut penser de plus grand", comprend ce qu'il entend, et ce qu'il comprend est dans son intellect, même s'il ne comprend pas que ce quelque chose est. Donc l'insensé aussi, il lui faut convenir qu'il y a bien dans l'intellect quelque chose de tel que rien ne se peut penser de plus grand, puisqu'il comprend ce qu'il entend, et que tout ce qui est compris est dans l'intellect.

l l Et il est bien certain que ce qui est tel que rien ne se peut penser de plus grand ne peut être seulement dans l'intellect. Car si c'est seulement dans l'intellect, on peut penser que ce soit aussi dans la réalité, ce qui est plus grand. Si donc ce qui est tel que rien ne peut se penser de plus grand est seulement dans l'intellect, cela même qui est tel que rien ne se peut penser de plus grand est tel qu'on peut penser quelque chose de plus grand ; mais cela est à coup sûr impossible. Il est donc hors de doute qu'il existe quelque chose de tel que rien ne se peut penser de plus grand, et cela tant dans l'intellect que dans la réalité.