La matematica nelle antiche civilt Egizi Sumeri Greci

La matematica nelle antiche civiltà Egizi, Sumeri, Greci IL GIARDINO DI ARCHIMEDE Unmuseo perla[matematica]

La matematica nell’antico Egitto Il papiro Rhind (c. 1650 a. C. ) Lungo 3 metri e alto 33 centimetri, contiene sul recto una tavola di frazioni e sul retro 84 problemi di aritmetica e geometria.

La matematica nell’antico Egitto Il papiro di Mosca (c. 1890 a. C. ) Lungo più di 5 metri e alto 8 centimetri. Contiene 25 problemi di aritmetica e geometria.

La matematica nell’antico Egitto I papiri di Kahun (c. 1800 a. C. ) Sono cinque papiri molto frammentari, che contengono tavole di frazioni e problemi simili a quelli del papiro Rhind.

La matematica nell’antico Egitto Il papiro di Reisner (c. 1800 a. C. ) Divisioni per 10 Il papiro di Berlino (c. 1800 a. C. ) Testi di medicina e di matematica. Forse una traccia del teorema di Pitagora. Il rotolo di cuoio(c. 1750 a. C. ) Tavole di frazioni. Le tavolette di legno (c. 2000 a. C. ) Cinque divisioni con le loro prove.

La scrittura dei numeri 1 10 10. 000 100 1000 1. 000

La scrittura dei numeri

La scrittura dei numeri 56 138 Proviamo a leggere

I numeri nei bassorilievi 46 11. 110 121. 200

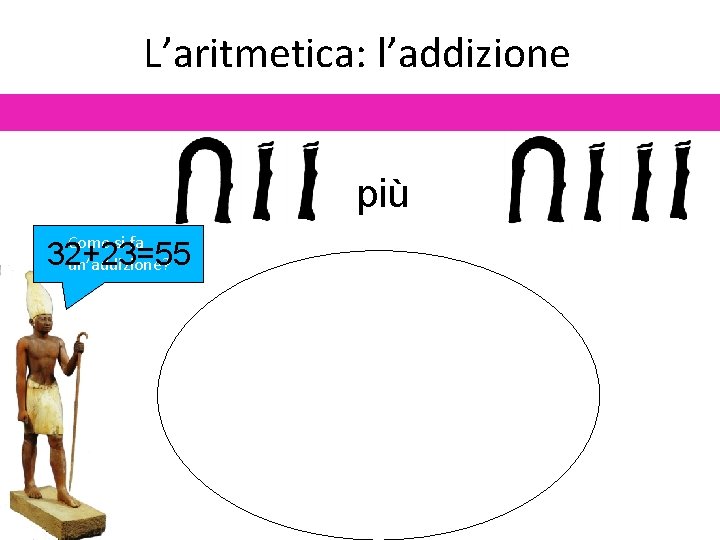
L’aritmetica: l’addizione più Come si fa un’addizione? 32+23=55

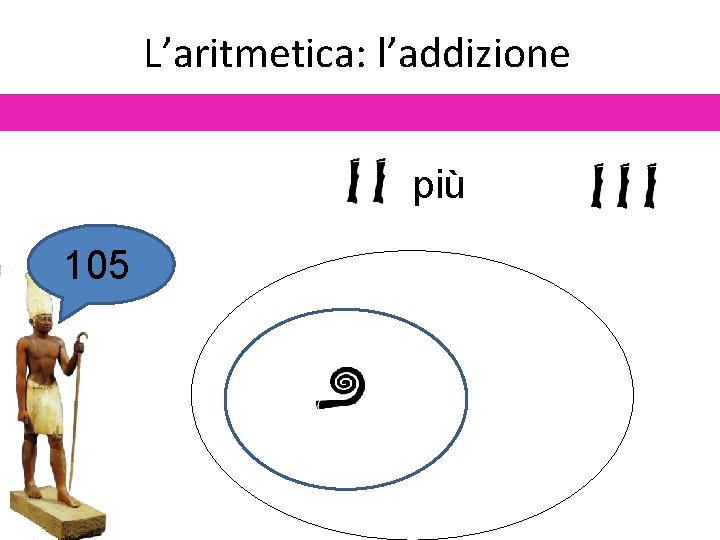
L’aritmetica: l’addizione più 105

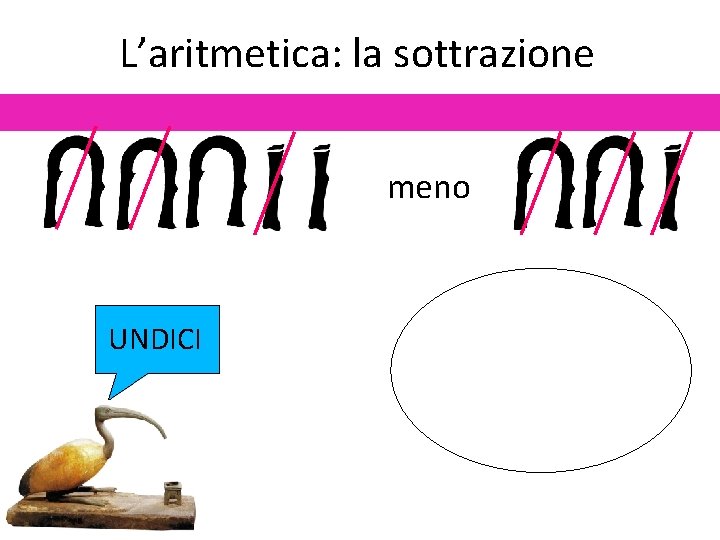
L’aritmetica: la sottrazione meno UNDICI

L’aritmetica: la sottrazione meno 108

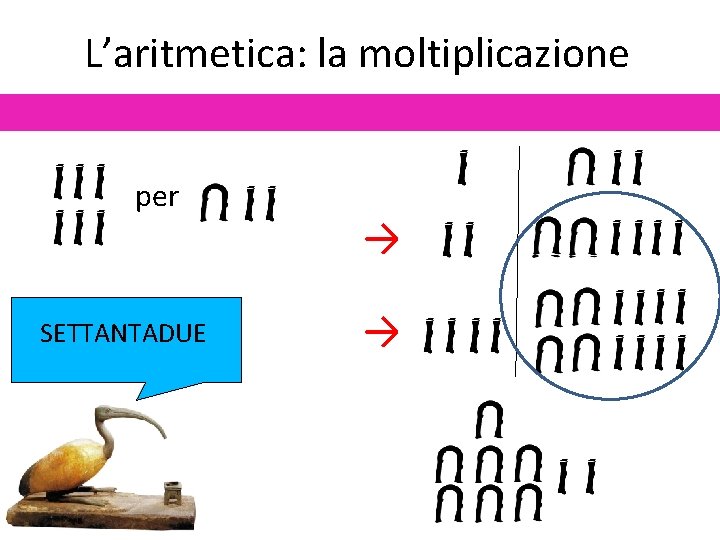
L’aritmetica: la moltiplicazione per SETTANTADUE → →

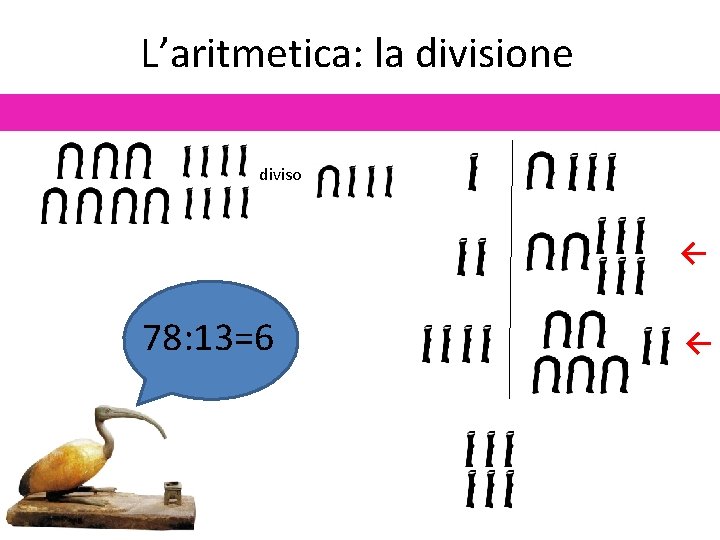
L’aritmetica: la divisione diviso ← 78: 13=6 ←

L’aritmetica: la divisione diviso ← 26: 4=6 resto 2 ←

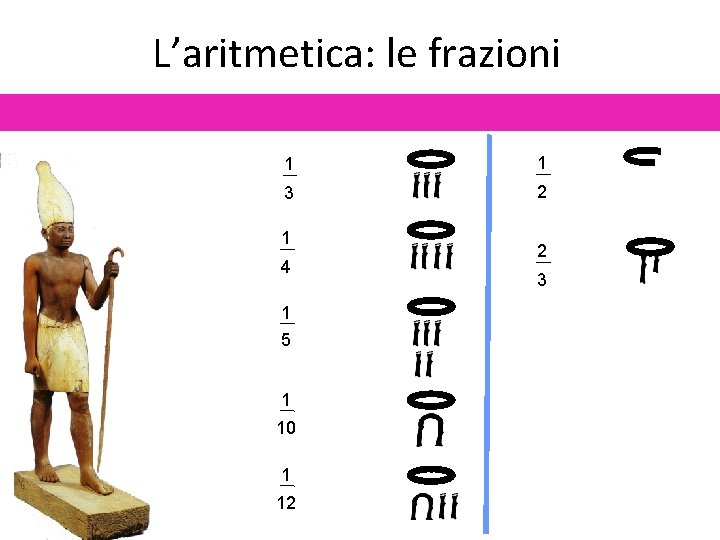
L’aritmetica: le frazioni 1 1 3 2 1 4 1 5 1 10 1 12 2 3

Le frazioni nei bassorilievi 1 40

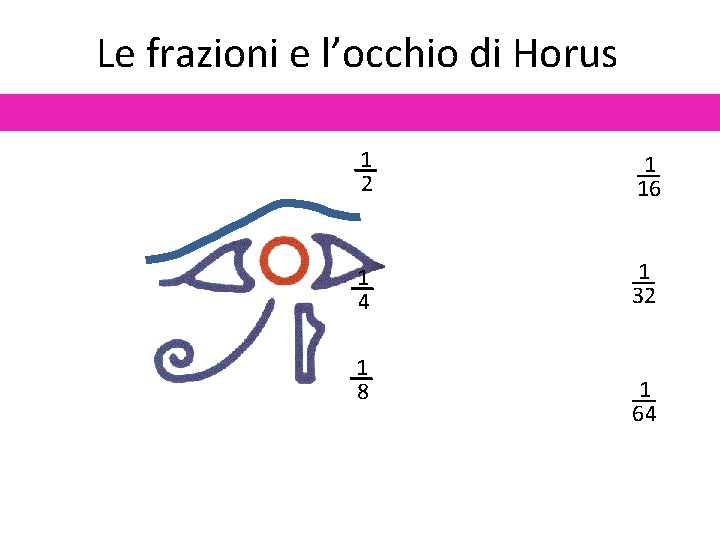
L’occhio di Horus

Le frazioni e l’occhio di Horus 1 2 1 16 1 4 1 32 1 8 1 64

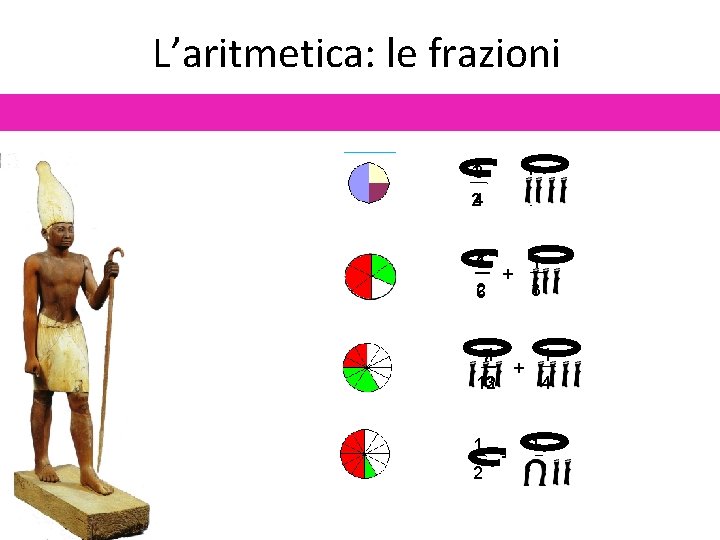
L’aritmetica: le frazioni 13 24 1 5 2 6 + + 1 4 1 3 71 + 12 3 1 2 + 1 4 1 12

Le moltiplicazioni con le frazioni 2 5 1 = 15 + 115 5 3 4 × 15 1 2 4 1 5 2 = 1 + 11 5 5 35 15 22 ++ 11 + 1 21 ++ 1 5 530 5 35 10 15

Le moltiplicazioni con le frazioni 12 15 per 3 RISULTATO: 1 12 15 2 24 36 1 1 3 15 1 1 1 3 5 15 ← ←

La composizione delle frazioni 1 1 1 3 5 15 Se dividiamo 1 in 30 parti ne abbiamo 10+6+2, cioè 18. Ma 18 = 15+3 Dividendo per 30, otteniamo 1 1 1 = 1 1 3 5 15 2 10

Le divisioni con le frazioni 63 diviso 12 12 24 48 6 3 1 2 4 1 2 1 4 resto RISULTATO: 5 1 4 ← ← ←

Un problema dal papiro Rhind Una quantità a cui si aggiunge la sua settima parte diventa 16 1 x x+ 77)= 16 8 7 (1+ 7 → 8 ? → 16

Un problema dal papiro Rhind Una quantità a cui si aggiunge la sua settima parte diventa 19 1 7 (1+ 7 )= 8 7 → 8 ? → 19

Un problema dal papiro Rhind Una quantità a cui si aggiunge la sua settima parte diventa 19 1 1 4 8 1 1 2 4 1 1 1 2 8 4 8 2 2 1 4 1 8 19: 8 = 2 2 × 7=16 1 2 4 82 4 16 49 2 1 ← ← ←

La geometria Il re Sesostri distribuì il territorio fra tutti gli egiziani, dando a ciascuno un lotto uguale, e secondo questa suddivisione si procurava le entrate, avendo imposto il pagamento di un tributo annuo. Se il fiume asportava da un podere una qualche parte, il proprietario, recatosi dal re, gli segnalava l’accaduto; egli allora mandava funzionari che osservavano e misuravano di quanto terreno era divenuto più piccolo, affinché per l’avvenire il proprietario pagasse in misura minore proporzionale il tributo. Io ritengo che in seguito a ciò abbia avuto origine la geometria e sia poi passata in Grecia. Erodoto, Storie

La geometria Nessuno dei miei contemporanei mi ha superato nel delineare le figure e nel dimostrare le loro proprietà, nemmeno gli arpedonapti dell’Egitto. Democrito

La geometria: le misure Misure di lunghezza 1 cubito ≈ 52 centimetri 1 cubito = 7 palmi = 28 dita 100 cubiti = 1 khet (rotolo di corda) ≈ 52 metri

La geometria: le misure Misure di superficie 1 setat = 1 khet quadrato = 10. 000 cubiti quadrati 1 cubito di terra = 1 khet x 1 cubito = 100 cubiti x 1 cubito 1000 di terra = 1000 cubiti di terra = 10 setat

La geometria: le misure Misure di capacità 1 cubito cubo ≈ 125 litri 1 cubito cubo = 30 hekat 1 hekat = 10 henu = 320 ro 1 khar = 20 hekat doppio hekat quadruplo hekat

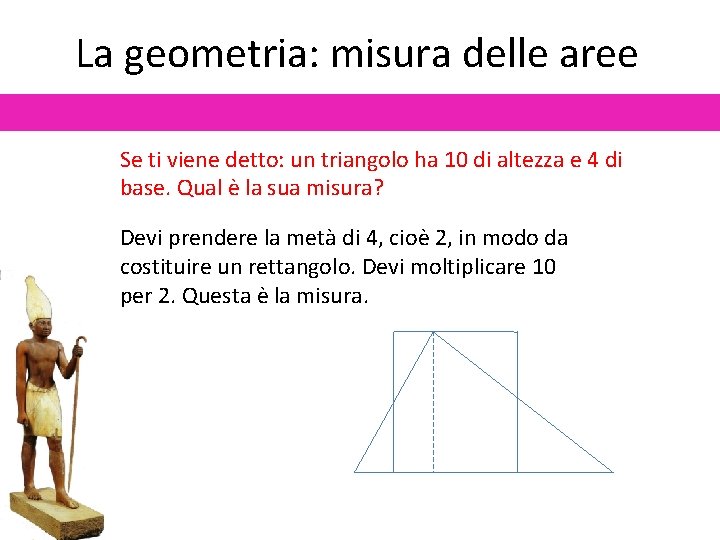
La geometria: misura delle aree Se ti viene detto: un triangolo ha 10 di altezza e 4 di base. Qual è la sua misura? Devi prendere la metà di 4, cioè 2, in modo da costituire un rettangolo. Devi moltiplicare 10 per 2. Questa è la misura.

La geometria: misura delle aree Metodo per calcolare un campo circolare di diametro 9. Qual è la sua area? Devi un nono del diametro, cioè 1: viene 8. π sottrarre ≈ 3, 1416 2 ( ) 16 moltiplicare Devi 8 otto volte: fa 64. Questa è l’area. = 3, 1605 9 A = πR 2 2 A = ( d) = ( 8 9 2 ) 16 9 R 2

La geometria: misura dei volumi Esempio di calcolo di un contenitore circolare di diametro 9 e altezza 10. Devi sottrarre la nona parte da 9: resta 8. Moltiplica 8 otto volte. Risultato: 64. Moltiplica 64 dieci volte; diventa 640. Questo è il suo contenuto. 10 9

La geometria: misura dei volumi Ti dicono: un tronco di piramide è di 6 cubiti in altezza verticale per 4 cubiti alla base per 2 cubiti alla sommità. Calcola il volume di questa piramide. Moltiplica questo 4 per 4: risultato 16. Moltiplica questo 2 per 2: risultato 4. Moltiplica 4 per 2: risultato 8. Addiziona 16, 8 e 4: risultato 28. Prendi 1/3 di 6: risultato 2. Moltiplica 28 per 2: risultato 56. Ecco che il volume è 56 (42 + 22 + 4 x 2) x 6 V= 3 (a 2 + b 2 + ab) h V= 3

La matematica nell’antico Egitto FINE