KS 4 Mathematics A 3 Formulae 1 of

KS 4 Mathematics A 3 Formulae 1 of 40 © Boardworks Ltd 2005

Contents A 3 Formulae A A 3. 1 Substituting into formulae A A 3. 2 Problems that lead to equations to solve A A 3. 3 Changing the subject of a formula A A 3. 4 Manipulating more difficult formulae A A 3. 5 Generating formulae 2 of 40 © Boardworks Ltd 2005

Formulae A formula is a special type of equation that links two or more physical variables. For example in the formula, P = 2(l + w) P represents the perimeter of a rectangle and l and w represent its length and width. We can use this formula to work out the perimeter of any rectangle given its length and width. We do this by substituting the values we are given into the formula. 3 of 40 © Boardworks Ltd 2005

Formulae Because formulae deal mainly with real-life quantities such as length, mass, temperature or time, the given variables often have units attached. Units shouldn’t be included in the formula itself. The units that have to be used are usually defined in the formula. For example, d S= t This formula doesn’t mean much unless we say “S is the average speed in m/s, d is the distance travelled in metres, and t is the time taken in seconds”. 4 of 40 © Boardworks Ltd 2005

Formulae d Use the formula S = to find the speed of a car that t travels 2 km in 1 minute and 40 seconds. Write the distance and the time using the correct units before substituting them into the formula, 2 kilometres = 2000 metres 1 minute and 40 seconds = 100 seconds Now substitute these numerical values into the formula, 2000 S= 100 We can write the units at the end. = 20 m/s 5 of 40 © Boardworks Ltd 2005

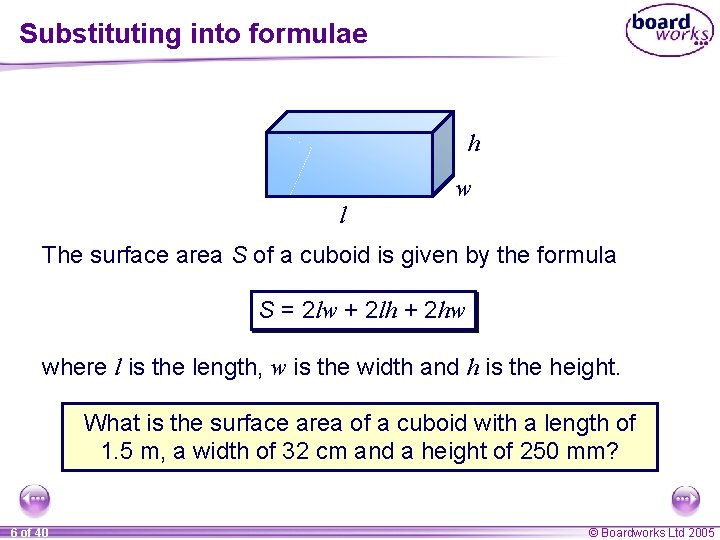
Substituting into formulae h w l The surface area S of a cuboid is given by the formula S = 2 lw + 2 lh + 2 hw where l is the length, w is the width and h is the height. What is the surface area of a cuboid with a length of 1. 5 m, a width of 32 cm and a height of 250 mm? 6 of 40 © Boardworks Ltd 2005

Substituting into formulae What is the surface area of a cuboid with a length of 1. 5 m, a width of 32 cm and a height of 250 mm? Before we can use the formula we must write all of the amounts using the same units. l = 150 cm, w = 32 cm and h = 25 cm Next, substitute the values into the formula without the units. S = 2 lw + 2 lh + 2 hw = (2 × 150 × 32) + (2 × 150 × 25) + (2 × 25 × 32) = 9600 + 7500 + 1600 = 18, 700 cm 2 Don’t forget to write the units in at the end. 7 of 40 © Boardworks Ltd 2005

Substituting into formulae The distance d, in metres, that an object falls after being dropped is given by the formula, d = 4. 9 t 2 where t is the time in seconds. Suppose a boy drops a rock from a 100 metre high cliff. How far will the rock have fallen after: a) 2 seconds b) 3 seconds c) 5 seconds? When t = 2, When t = 3, When t = 5, d = 4. 9 × 22 = 4. 9 × 4 = 19. 6 metres d = 4. 9 × 32 = 4. 9 × 9 = 44. 1 metres d = 4. 9 × 52 = 4. 9 × 25 = 122. 5 metres 8 of 40 © Boardworks Ltd 2005

Substituting into formulae 9 of 40 © Boardworks Ltd 2005

Contents A 3 Formulae A A 3. 1 Substituting into formulae A A 3. 2 Problems that lead to equations to solve A A 3. 3 Changing the subject of a formula A A 3. 4 Manipulating more difficult formulae A A 3. 5 Generating formulae 10 of 40 © Boardworks Ltd 2005

Problems that lead to equations to solve Formulae are usually (but not always) arranged so that a single variable is written on the left-hand side of the equals sign. For example, in the formula v = u + at v is called the subject of the formula. If we are given the values of u, a and t, we can find v by substituting these values into the formula. Suppose instead that we are given to values of v, u and a, and asked to find t. When these values are substituted we are left with an equation to solve in t. 11 of 40 © Boardworks Ltd 2005

Problems that lead to equations to solve For example, suppose v = 20, u = 5 and a = 3. Find t. Substituting these values into v = u + at gives us the equation, 20 = 5 + 3 t We can then solve this equation as usual. swap both sides: subtract 5 from both sides: divide both sides by 3: 12 of 40 5 + 3 t = 20 3 t = 15 t = 5 seconds © Boardworks Ltd 2005

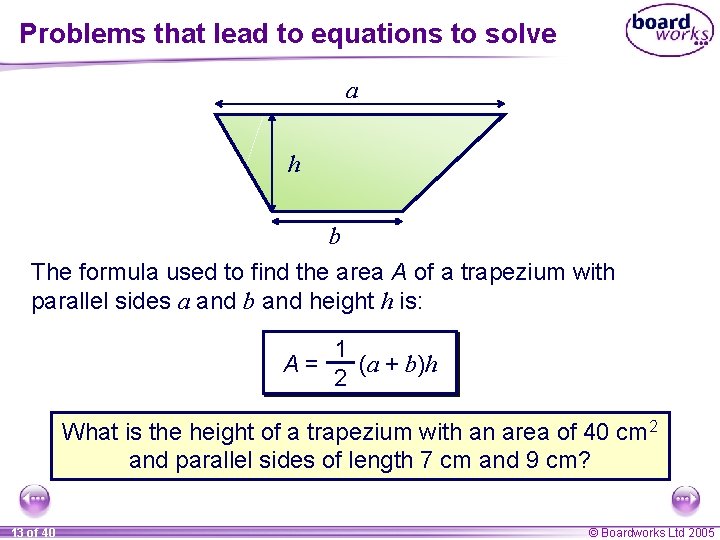
Problems that lead to equations to solve a h b The formula used to find the area A of a trapezium with parallel sides a and b and height h is: A= 1 (a + b)h 2 What is the height of a trapezium with an area of 40 cm 2 and parallel sides of length 7 cm and 9 cm? 13 of 40 © Boardworks Ltd 2005

Problems that lead to equations to solve Substituting A = 40, a = 7 and b = 9 into A = Simplifying, 40 = 1 (7 + 9)h 2 40 = 1 × 16 h 2 1 (a + b)h gives 2 40 = 8 h swap both sides: divide by 8: 8 h = 40 h=5 So the height of the trapezium is 5 cm. 14 of 40 © Boardworks Ltd 2005

Problems that lead to equations to solve 15 of 40 © Boardworks Ltd 2005

Contents A 3 Formulae A A 3. 1 Substituting into formulae A A 3. 2 Problems that lead to equations to solve A A 3. 3 Changing the subject of a formula A A 3. 4 Manipulating more difficult formulae A A 3. 5 Generating formulae 16 of 40 © Boardworks Ltd 2005

The subject of a formula Here is a formula you may know from physics: V = IR where V is voltage, I is current and R is resistance. V is called the subject of the formula. The subject of a formula always appears in front of the equals sign without any other numbers or operations. Sometimes it is useful to rearrange a formula so that one of the other variables is the subject of the formula. Suppose, for example, that we want to make I the subject of the formula V = IR. 17 of 40 © Boardworks Ltd 2005

Changing the subject of the formula V is the subject of this formula The formula: V = IR can be written as a function diagram: I ×R V ÷R V The inverse of this is: I So: V I= R 18 of 40 I is now the subject of this formula © Boardworks Ltd 2005

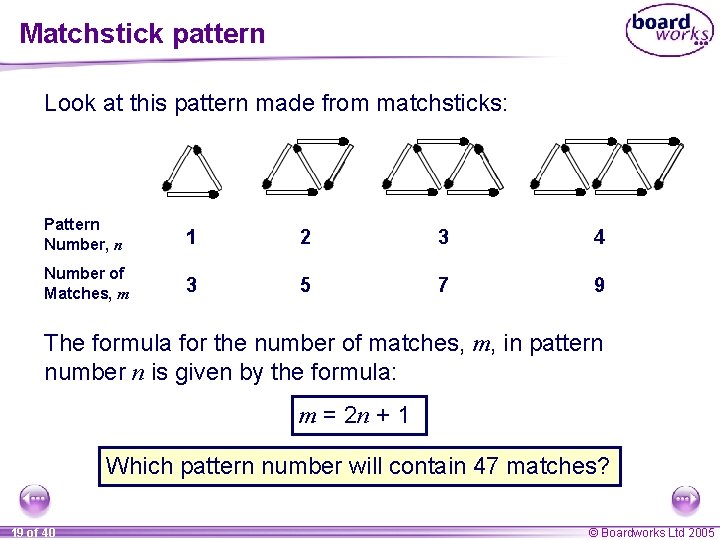
Matchstick pattern Look at this pattern made from matchsticks: Pattern Number, n 1 2 3 4 Number of Matches, m 3 5 7 9 The formula for the number of matches, m, in pattern number n is given by the formula: m = 2 n + 1 Which pattern number will contain 47 matches? 19 of 40 © Boardworks Ltd 2005

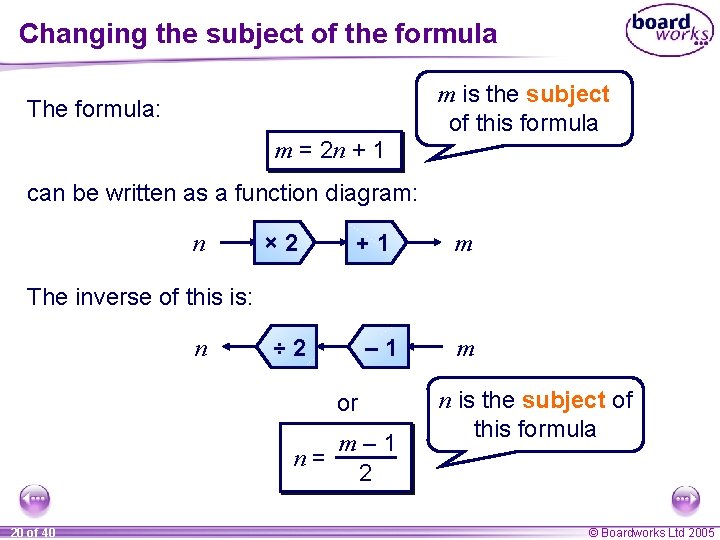
Changing the subject of the formula m is the subject of this formula The formula: m = 2 n + 1 can be written as a function diagram: n × 2 +1 m The inverse of this is: n ÷ 2 – 1 or m– 1 n= 2 20 of 40 m n is the subject of this formula © Boardworks Ltd 2005

Changing the subject of the formula To find out which pattern will contain 47 matches, substitute 47 into the rearranged formula. m– 1 n= 2 47 – 1 n= 2 n= 46 2 n = 23 So, the 23 rd pattern will contain 47 matches. 21 of 40 © Boardworks Ltd 2005

Changing the subject of the formula We can also change the subject by performing the same operations on both sides of the equals sign. For example, to make C the subject of 9 C F= + 32 5 subtract 32: multiply by 5: divide by 9: 9 C F – 32 = 5 5(F – 32) = 9 C 5(F – 32) =C 9 5(F – 32) C= 9 22 of 40 © Boardworks Ltd 2005

Change the subject of the formula 1 23 of 40 © Boardworks Ltd 2005

Find the equivalent formulae 24 of 40 © Boardworks Ltd 2005

Contents A 3 Formulae A A 3. 1 Substituting into formulae A A 3. 2 Problems that lead to equations to solve A A 3. 3 Changing the subject of a formula A A 3. 4 Manipulating more difficult formulae A A 3. 5 Generating formulae 25 of 40 © Boardworks Ltd 2005

Formulae where the subject appears twice Sometimes the variable that we are making the subject of a formula appears twice. For example, S = 2 lw + 2 lh + 2 hw where S is the surface area of a cuboid, l is its length, w is its width and h is its height. Make w the subject of the formula. To do this we must collect all terms containing w on the same side of the equals sign. We can then isolate w by factorizing. 26 of 40 © Boardworks Ltd 2005

Formulae where the subject appears twice S = 2 lw + 2 lh + 2 hw Let’s start by swapping the left-hand side and the right-hand side so that the terms with w’s are on the left. 2 lw + 2 lh + 2 hw = S subtract 2 lh from both sides: 2 lw + 2 hw = S – 2 lh factorize: w(2 l + 2 h) = S – 2 lh divide by 2 l + 2 h: 27 of 40 S – 2 lh w = 2 l + 2 h © Boardworks Ltd 2005

Formulae involving fractions When a formula involves fractions we usually remove these by multiplying before changing the subject. For example, if two resistors with a resistance a and b ohms respectively, are arranged in parallel their total resistance R ohms can be found using the formula, 1 1 1 = + a b R aΩ bΩ Make R the subject of the formula 28 of 40 © Boardworks Ltd 2005

Formulae involving fractions 1 1 1 = + a b R multiply through by Rab: Rab Rab = + a b R simplify: ab = Rb + Ra factorize: ab = R(b + a) divide both sides by a + b: ab =R a+b ab R= a+b 29 of 40 © Boardworks Ltd 2005

Formulae involving powers and roots The length c of the hypotenuse of a right-angled triangle is given by c = √a 2 + b 2 where a and b are the lengths of the shorter sides. Make a the subject of the formula square both sides: subtract b 2 from both sides: square root both sides: c 2 = a 2 + b 2 c 2 – b 2 = a 2 √c 2 – b 2 = a a = √c 2 – b 2 30 of 40 © Boardworks Ltd 2005

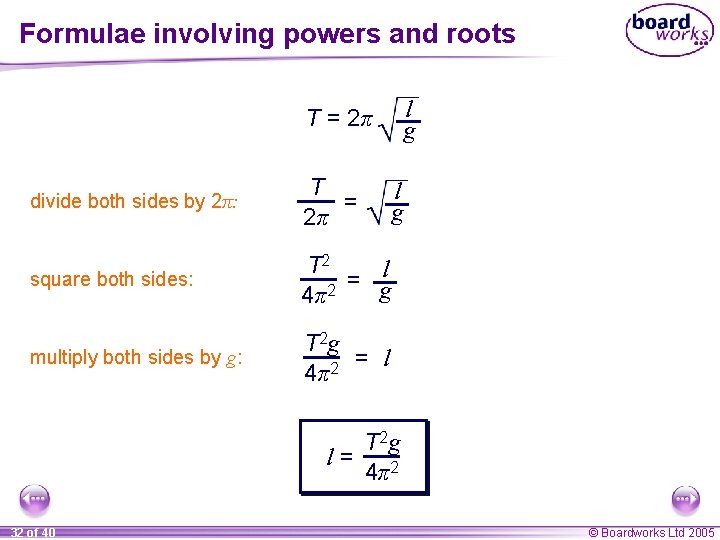
Formulae involving powers and roots The time T needed for a pendulum to make a complete swing is T = 2π gl where l is the length of the pendulum and g is acceleration due to gravity. Make l the subject of the formula When the variable that we wish to make the subject appears under a square root sign, we should isolate it on one side of the equation and then square both sides. 31 of 40 © Boardworks Ltd 2005

Formulae involving powers and roots l g T = 2π divide both sides by 2π: T = 2π square both sides: T 2 l = g 4π2 multiply both sides by g: T 2 g = l 2 4π l g T 2 g l= 4π2 32 of 40 © Boardworks Ltd 2005

Change the subject of the formula 2 33 of 40 © Boardworks Ltd 2005

Contents A 3 Formulae A A 3. 1 Substituting into formulae A A 3. 2 Problems that lead to equations to solve A A 3. 3 Changing the subject of a formula A A 3. 4 Manipulating more difficult formulae A A 3. 5 Generating formulae 34 of 40 © Boardworks Ltd 2005

Writing formulae Write a formula to work out, 1) the cost, c, of b boxes of crisps at £ 3 each c = 3 b 2) the distance left, d, of a 500 km journey after travelling k km d = 500 – k 3) the cost person, c, if a meal costing m pounds is shared between p people m c= p 35 of 40 © Boardworks Ltd 2005

Writing formulae 4) the number of seats in a theatre, n, with 25 seats in each row, r n = 25 r 5) the age of a boy Andy, a, if he is 5 years older than his sister Betty, b a=b+5 6) the average weight, w, of Alex who weighs a kg, Bob who weighs b kg and Claire who weighs c kg. a+b+c w= 3 36 of 40 © Boardworks Ltd 2005

Writing formulae A window cleaner charges a £ 10 call-out fee plus £ 7 for every window that he cleans. Write a formula to find the total cost C when n windows are cleaned. C = 7 n + 10 Using this formula, how much would it cost to clean all 105 windows of Formula Mansion? We substitute the value into the formula, C = 7 × 105 + 10 = 735 + 10 = 745 It will cost £ 745. 37 of 40 © Boardworks Ltd 2005

Writing formulae C = 7 n + 10 At another house the window cleaner made £ 94. How many windows did he have to clean? We substitute this value into the formula to give an equation, 94 = 7 n + 10 swap both sides: 7 n + 10 = 94 subtract 10 from both sides: 7 n = 84 n = 12 He cleaned 12 windows. 38 of 40 © Boardworks Ltd 2005

Using formulae to write mathematical rules When conducting a mathematical investigation, it is usually necessary to use formulae to write rules and generalizations. For example, Sophie is investigating patterns of shaded squares on a numbered grid. She starts by looking at arrangements of numbers in two by two squares on a 100 square grid. For example, 39 of 40 34 35 44 45 She notices that the sum of the numbers in a two by two square is always equal to four times the number in the top lefthand square plus 22. Sophie writes this as a formula. © Boardworks Ltd 2005

Number grid patterns 40 of 40 © Boardworks Ltd 2005