Kompetenzorientierter Mathematikunterricht Logischdeduktiv strukturieren Eine kognitive Herausforderung Am

















- Slides: 37

Kompetenzorientierter Mathematikunterricht Logisch-deduktiv strukturieren Eine kognitive Herausforderung (Am Beispiel der Elementargeometrie) H. Freudigmann 2009 1

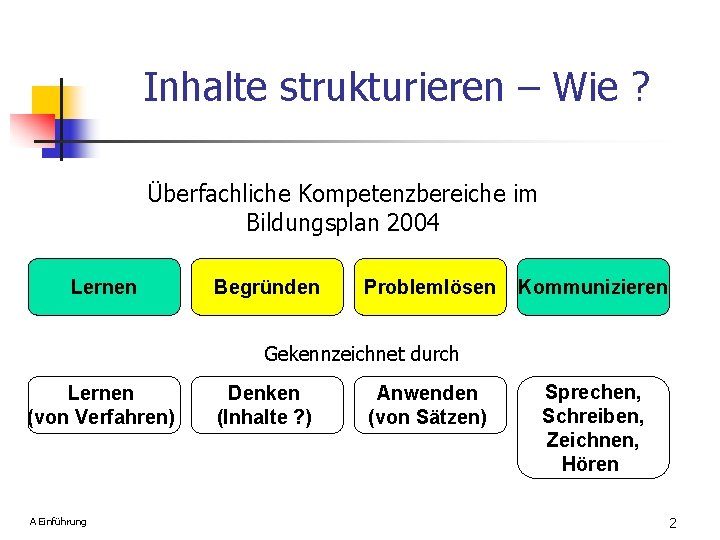
Inhalte strukturieren – Wie ? Überfachliche Kompetenzbereiche im Bildungsplan 2004 Lernen Begründen Problemlösen Kommunizieren Gekennzeichnet durch Lernen (von Verfahren) A Einführung Denken (Inhalte ? ) Anwenden (von Sätzen) Sprechen, Schreiben, Zeichnen, Hören 2

„Natürliche“ Strukturierung der Mathematik Einzigartig für die Mathematik: Mathematik kann man axiomatisch-deduktiv ordnen Das ist mehr als z. B. den Pythagoras zu kennen. Das betrifft das „Ganze“ der Mathematik, ihren Kern. A Einführung 3

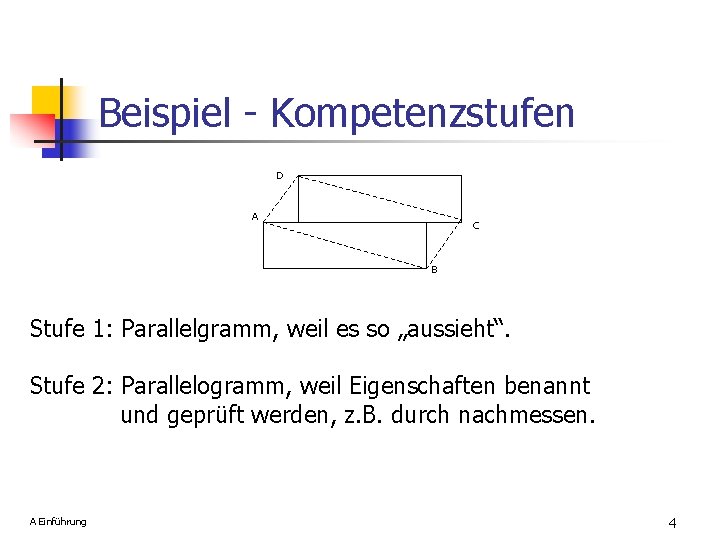
Beispiel - Kompetenzstufen D A C B Stufe 1: Parallelgramm, weil es so „aussieht“. Stufe 2: Parallelogramm, weil Eigenschaften benannt und geprüft werden, z. B. durch nachmessen. A Einführung 4

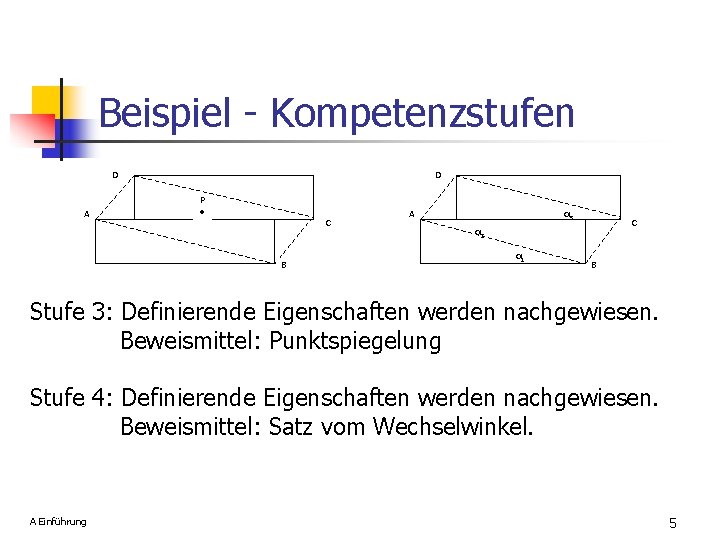
Beispiel - Kompetenzstufen D A D P ● C B α 3 A C α 2 α 1 B Stufe 3: Definierende Eigenschaften werden nachgewiesen. Beweismittel: Punktspiegelung Stufe 4: Definierende Eigenschaften werden nachgewiesen. Beweismittel: Satz vom Wechselwinkel. A Einführung 5

Beispiel - Kompetenzstufen D A C B Stufe 5: Zielgerichtetes, strukturiertes Vorgehen. „Ich will Parallelität nachweisen, muss also argumentieren mit: S. v. Stufenwinkel, S. v. Wechselwinkel, Kongruenzsätzen, S. v. Parallelogramm, Strahlensätze, S. d. Pythagoras (? ), . . A Einführung 6

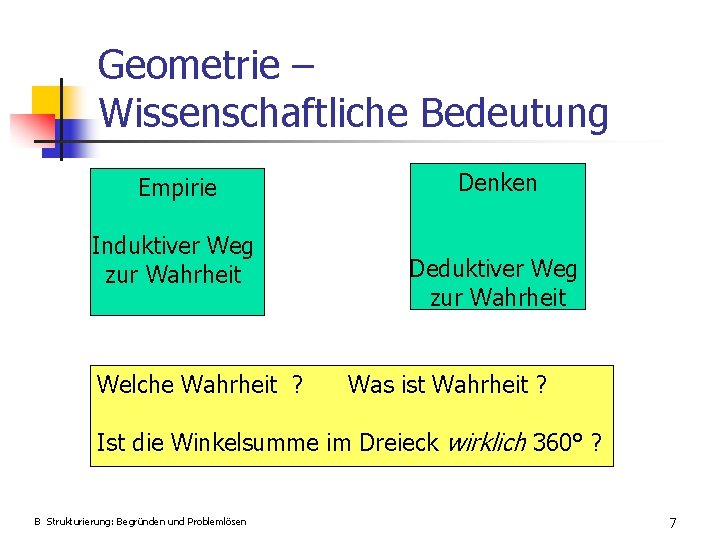
Geometrie – Wissenschaftliche Bedeutung Empirie Induktiver Weg zur Wahrheit Welche Wahrheit ? Denken Deduktiver Weg zur Wahrheit Was ist Wahrheit ? Ist die Winkelsumme im Dreieck wirklich 360° ? B Strukturierung: Begründen und Problemlösen 7

Begründungsbasis I Die anschauliche Verwendung von Kongruenzabbildungen und ihrer Eigenschaften bilden die erste Begründungsbasis der Schulgeometrie am Anfang der Klasse 7. Wenn Winkel achsen- oder punktsymmetrisch liegen, dann sind sie gleich weit. Wenn Strecken achsen- oder punktsymmetrisch liegen, dann sind sie - gleich lang - parallel. B Strukturierung: Begründen und Problemlösen 8

Begründungsbasis II n n n Nebenwinkelsatz Scheitelwinkelsatz Stufenwinkelsatz² Wechselwinkelsatz² Satz von der Mittelsenkrechten ² n n S. v. d. Winkelhalbierenden² S. v. gleichschenkligen Dreieck² Satz vom Parallelogramm² S. v. d. Mittelparallelen im Dreieck ²Satz und Kehrsatz B Strukturierung: Begründen und Problemlösen 9

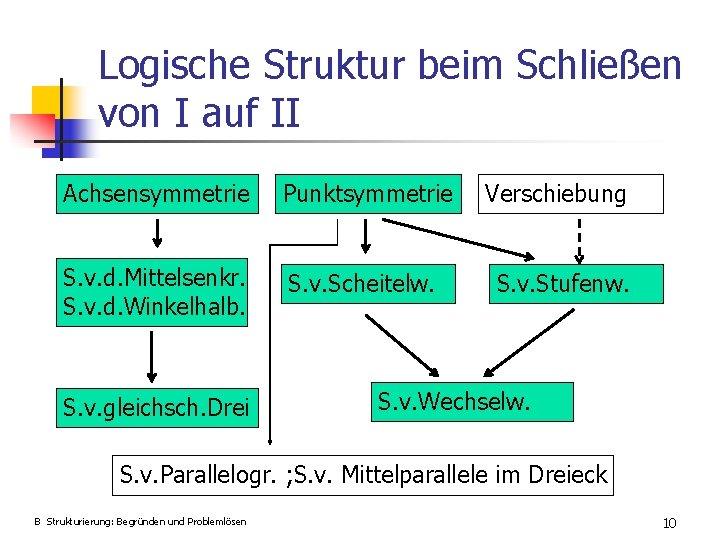
Logische Struktur beim Schließen von I auf II Achsensymmetrie Punktsymmetrie Verschiebung S. v. d. Mittelsenkr. S. v. d. Winkelhalb. S. v. Scheitelw. S. v. Stufenw. S. v. gleichsch. Drei S. v. Wechselw. S. v. Parallelogr. ; S. v. Mittelparallele im Dreieck B Strukturierung: Begründen und Problemlösen 10

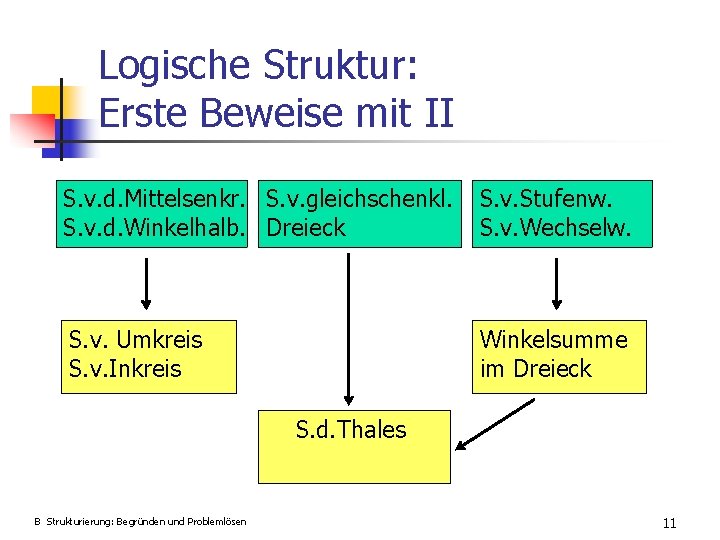
Logische Struktur: Erste Beweise mit II S. v. d. Mittelsenkr. S. v. gleichschenkl. S. v. d. Winkelhalb. Dreieck S. v. Stufenw. S. v. Wechselw. S. v. Umkreis S. v. Inkreis Winkelsumme im Dreieck S. d. Thales B Strukturierung: Begründen und Problemlösen 11

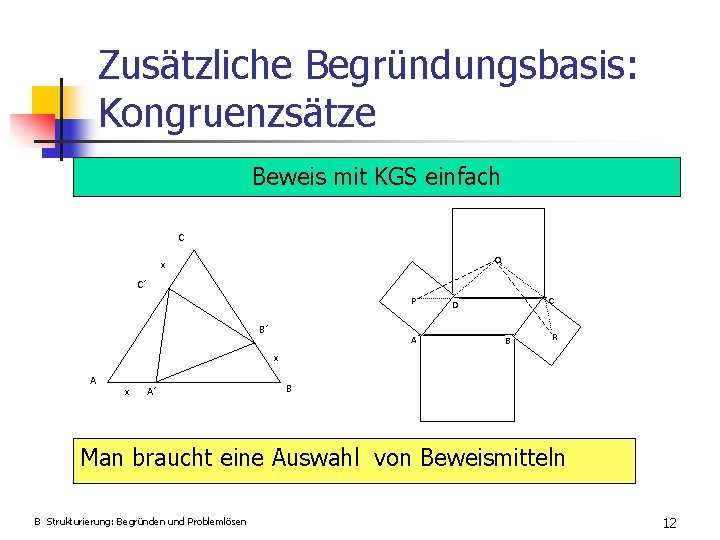
Zusätzliche Begründungsbasis: Kongruenzsätze Beweis mit KGS einfach C Q x C´ P B´ A C D B R x A´ B Man braucht eine Auswahl von Beweismitteln B Strukturierung: Begründen und Problemlösen 12

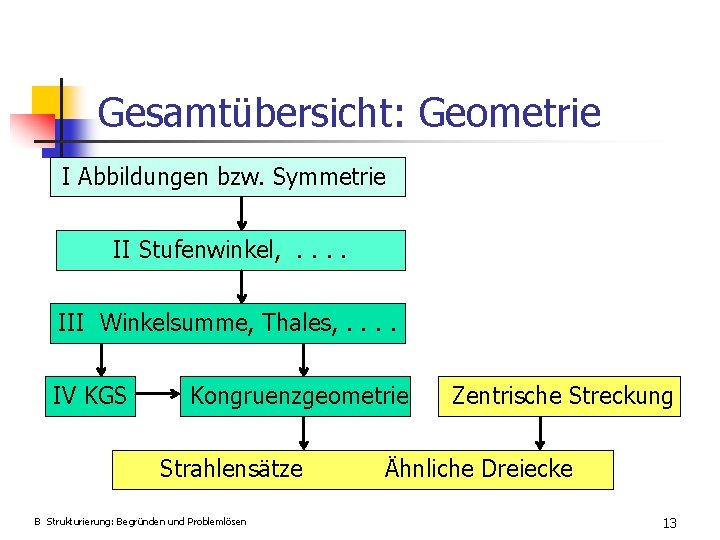
Gesamtübersicht: Geometrie I Abbildungen bzw. Symmetrie II Stufenwinkel, . . III Winkelsumme, Thales, . . IV KGS Kongruenzgeometrie Strahlensätze B Strukturierung: Begründen und Problemlösen Zentrische Streckung Ähnliche Dreiecke 13

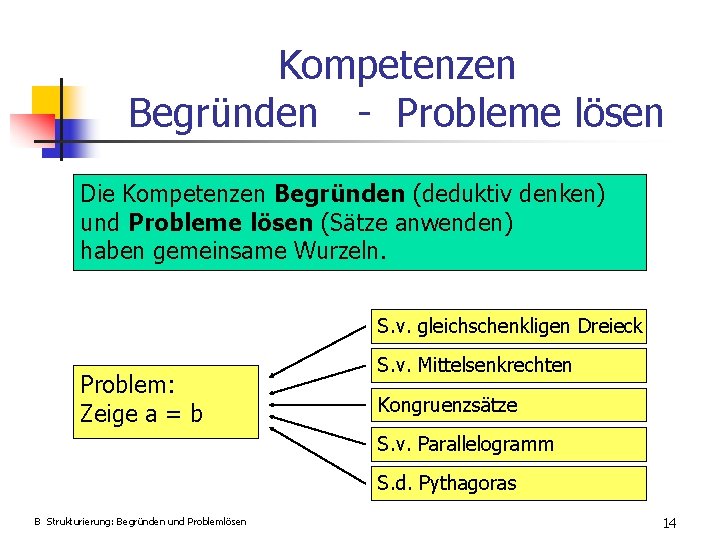
Kompetenzen Begründen - Probleme lösen Die Kompetenzen Begründen (deduktiv denken) und Probleme lösen (Sätze anwenden) haben gemeinsame Wurzeln. S. v. gleichschenkligen Dreieck Problem: Zeige a = b S. v. Mittelsenkrechten Kongruenzsätze S. v. Parallelogramm S. d. Pythagoras B Strukturierung: Begründen und Problemlösen 14

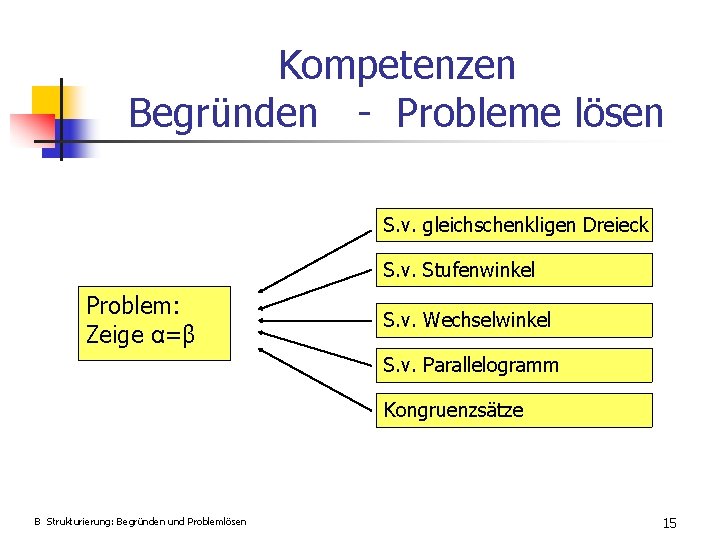
Kompetenzen Begründen - Probleme lösen S. v. gleichschenkligen Dreieck S. v. Stufenwinkel Problem: Zeige α=β S. v. Wechselwinkel S. v. Parallelogramm Kongruenzsätze B Strukturierung: Begründen und Problemlösen 15

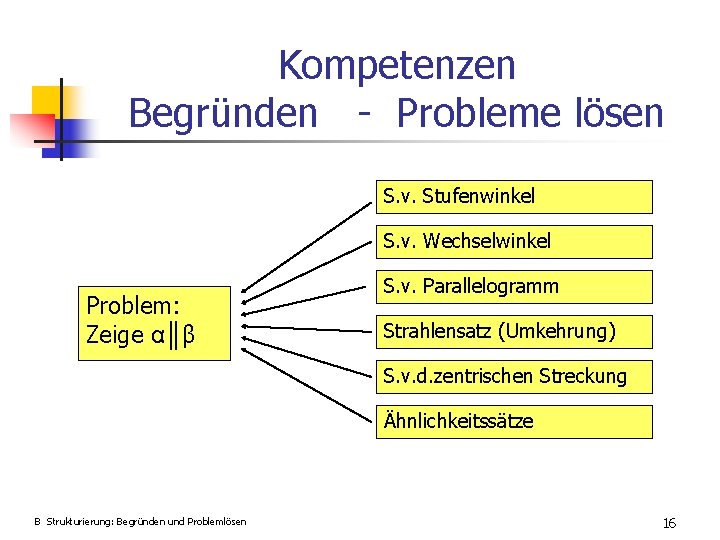
Kompetenzen Begründen - Probleme lösen S. v. Stufenwinkel S. v. Wechselwinkel Problem: Zeige α║β S. v. Parallelogramm Strahlensatz (Umkehrung) S. v. d. zentrischen Streckung Ähnlichkeitssätze B Strukturierung: Begründen und Problemlösen 16

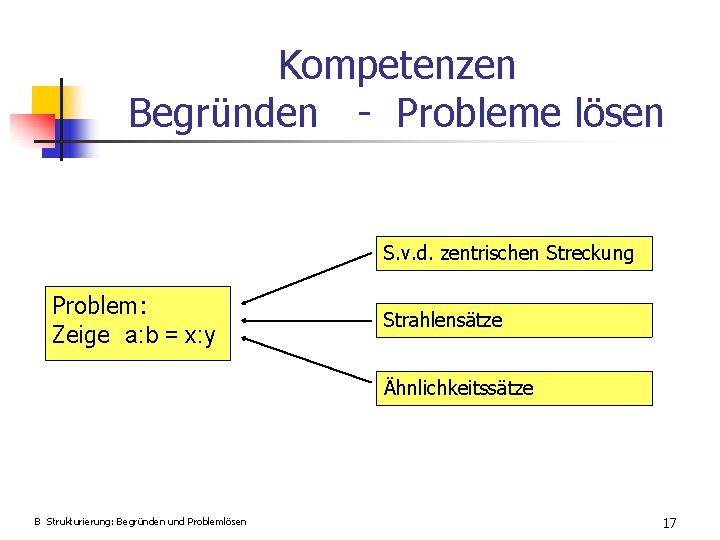
Kompetenzen Begründen - Probleme lösen S. v. d. zentrischen Streckung Problem: Zeige a: b = x: y Strahlensätze Ähnlichkeitssätze B Strukturierung: Begründen und Problemlösen 17

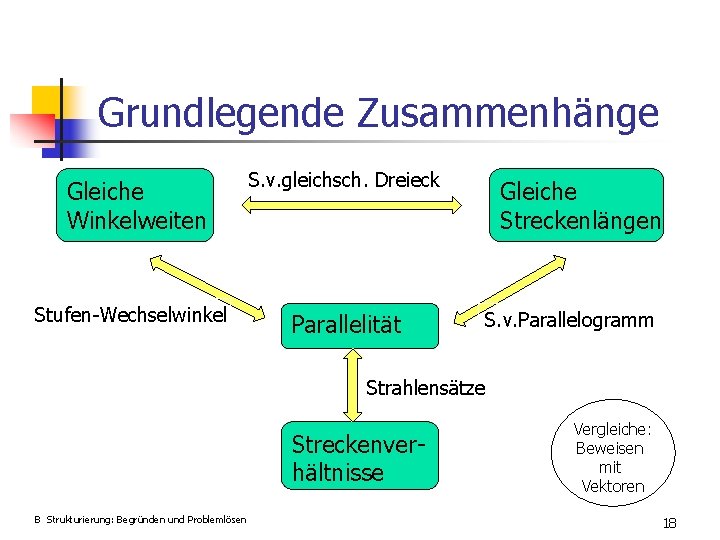
Grundlegende Zusammenhänge Gleiche Winkelweiten S. v. gleichsch. Dreieck Stufen-Wechselwinkel Parallelität Gleiche Streckenlängen S. v. Parallelogramm Strahlensätze Streckenverhältnisse B Strukturierung: Begründen und Problemlösen Vergleiche: Beweisen mit Vektoren 18

Im Unterricht: Beweismittel offenlegen Das Beweisen und Probleme lösen zum Thema machen. Anleitung: Wie beweist man (löst man Probleme) ? Beweismittel (Problemlösemittel) sind präsent. Beweismittel präsent auf Plakaten S. v. Stufenwinkel 1 S. v. Wechselwinkel 1 S. v. Nebenwinkel g║h → α = β α + β = 180° S. v. Stufenwinkel 2 S. v. Wechselwinkel 2 S. v. Scheitelwinkel g║h ← α = β α=β B Strukturierung: Begründen und Problemlösen 19

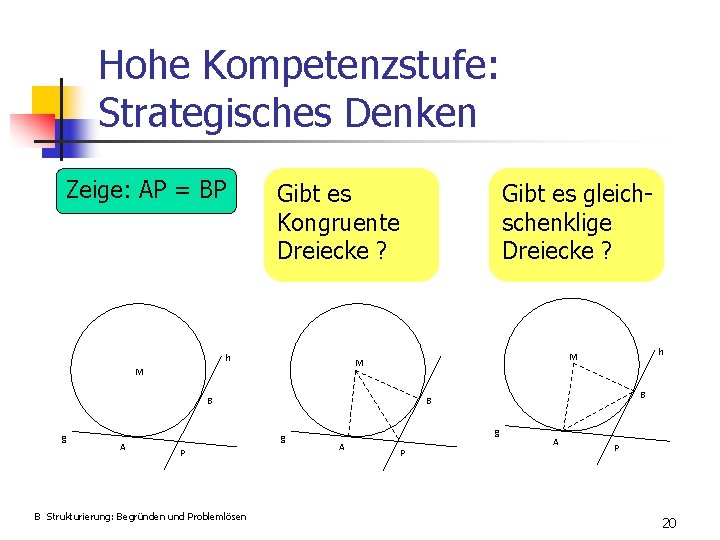
Hohe Kompetenzstufe: Strategisches Denken Zeige: AP = BP Gibt es Kongruente Dreiecke ? h Gibt es gleichschenklige Dreiecke ? M A g P B Strukturierung: Begründen und Problemlösen B B B g h M M g A P 20

Fachkonferenz: Arbeitsauftrag (Vorschlag) 1 (Material S. 12 – 16) a) Welche Beweismittel der Elementargeometrie sollen den Schülern in den Klassenstufen 6 (7, 8, 9, 10) jeweils zur Verfügung stehen ? b) Wie stellt sich der deduktive Zusammenhang dieser Beweismittel dar ? (Zum Beispiel: Werden z. B. die KGS anschaulich oder mittels Kongruenzabbildungen begründet ? ) 2 (Material S. 23 -24) Über welche Strategien für das Beweisen und Problemlösen in der Elementargeometrie sollen die Schüler in den Klassenstufen 6 (7, 8, 9, 10) jeweils verfügen ? B Strukturierung: Begründen und Problemlösen 21

Im Unterricht: Die Mittelsenkrechte Logisch nicht befriedigend: Die Mittelsenkrechte einer Strecke AB ist die Menge aller Punkte, die von A und B den gleichen Abstand haben. Die Mittelsenkrechte einer Strecke AB ist die Ortslinie aller Punkte, die von A und B den gleichen Abstand haben. Unklar beleiben: Wie ist Mittelsenkrechte festgelegt ? Wie wird sie verwendet ? (Was ist der Sinn des Begriffs? C Umsetzungsbeispiele 22

Im Unterricht: Die Mittelsenkrechte Definition: Zu einer Strecke AB heißt eine Gerade m Mittelsenkrechte, wenn sie durch die Mitte von AB verläuft und zu AB orthogonal ist. Satz 1: Wenn ein Punkt P auf der Mittelsenkrechten m von A und B liegt, dann hat P von A und von B den gleichen Abstand. Satz 2: Wenn ein Punkt P von zwei Punkten A und B den gleichen Abstand hat, dann liegt P auf der Mittelsenkrechten m von AB. C Umsetzungsbeispiele 23

Im Unterricht: Die Mittelsenkrechte Definition: Zu einer Strecke AB heißt eine Gerade m Mittelsenkrechte, wenn sie durch die Mitte von AB verläuft und zu AB orthogonal ist. Satz 1: Wenn ein Punkt P auf der Mittelsenkrechten m von A und B liegt, dann hat P von A und von B den gleichen Abstand. Beweis: m ist Symmetrieachse von AB. P liegt auf m (Voraussetzung) A und B liegen symmetrisch; AP und BP liegen symmetrisch. P Symmetrische Strecken sind gleich lang. Beweismittel: a) Die MS einer Strecke ist Symmetrieachse der Strecke. b) Symmetrisch liegende Strecken sind gleich lang. C Umsetzungsbeispiele A B m 24

Im Unterricht: Die Mittelsenkrechte Satz 2: Wenn ein Punkt P von zwei Punkten A und B den gleichen Abstand hat, dann liegt P auf der Mittelsenkrechten m von A und B. Beweis mit Kontrainduktion: Liegt Q nicht auf m, dann AQ≠BQ QR + RB > QB (Dreiecksungleichung) und RA = RB Deshalb QR + RA > QB, Deshalb AQ > BQ. Diese Begründung ist nur mit erheblichen formalen Abstrichen in der Schule zu leisten. C Umsetzungsbeispiele P Q R A B m 25

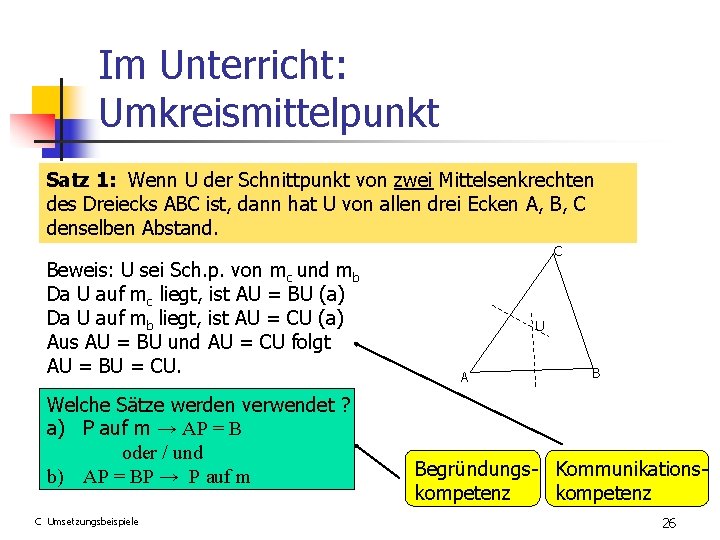
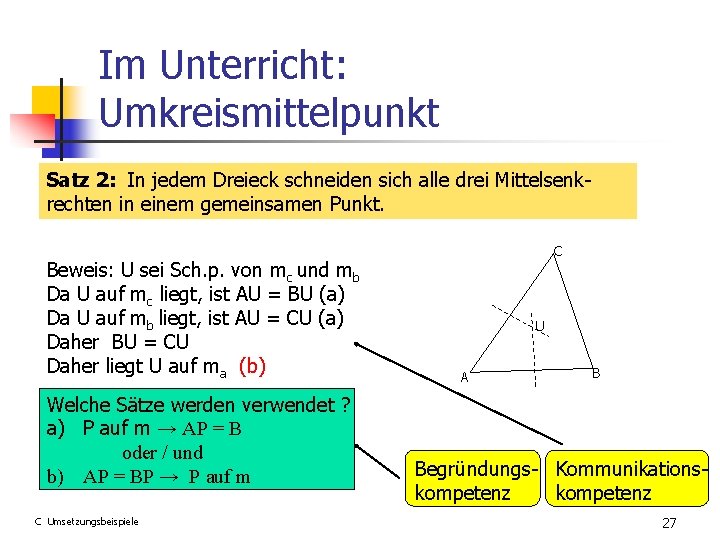
Im Unterricht: Umkreismittelpunkt Satz 1: Wenn U der Schnittpunkt von zwei Mittelsenkrechten des Dreiecks ABC ist, dann hat U von allen drei Ecken A, B, C denselben Abstand. Beweis: U sei Sch. p. von mc und mb Da U auf mc liegt, ist AU = BU (a) Da U auf mb liegt, ist AU = CU (a) Aus AU = BU und AU = CU folgt AU = BU = CU. Welche Sätze werden verwendet ? a) P auf m → AP = B oder / und b) AP = BP → P auf m C Umsetzungsbeispiele C U A B Begründungs- Kommunikationskompetenz 26

Im Unterricht: Umkreismittelpunkt Satz 2: In jedem Dreieck schneiden sich alle drei Mittelsenkrechten in einem gemeinsamen Punkt. Beweis: U sei Sch. p. von mc und mb Da U auf mc liegt, ist AU = BU (a) Da U auf mb liegt, ist AU = CU (a) Daher BU = CU Daher liegt U auf ma (b) Welche Sätze werden verwendet ? a) P auf m → AP = B oder / und b) AP = BP → P auf m C Umsetzungsbeispiele C U A B Begründungs- Kommunikationskompetenz 27

Fachkonferenz: Arbeitsauftrag (Vorschlag) 3 (Material S. 27 – 30) Am Beispiel Mittelsenkrechte / Satz vom Umkreis: Welches Niveau streben wir bei der Ausprägung der Begründungskompetenz an im Hinblick auf - die Formulierung der Sätze ? - die genaue Identifizierung der verwendeten Beweismittel ? - die schriftliche Dokumentation einer Begründung / eines Beweises ? 28

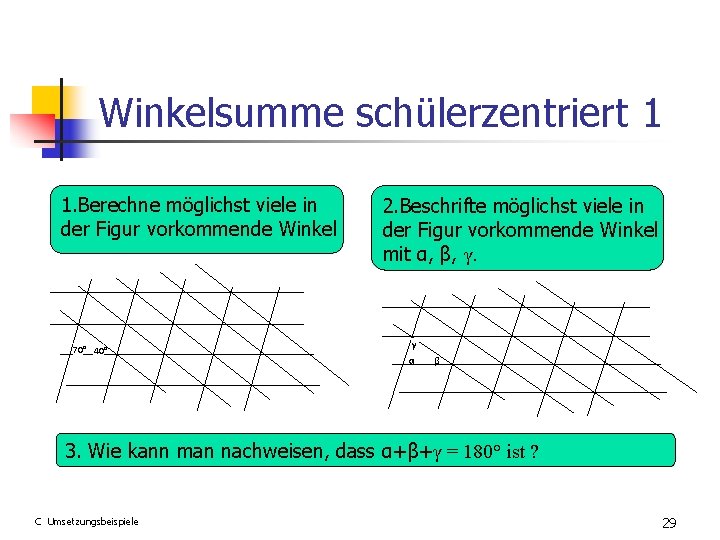
Winkelsumme schülerzentriert 1 1. Berechne möglichst viele in der Figur vorkommende Winkel 70° 40° 2. Beschrifte möglichst viele in der Figur vorkommende Winkel mit α, β, γ. γ α β 3. Wie kann man nachweisen, dass α+β+γ = 180° ist ? C Umsetzungsbeispiele 29

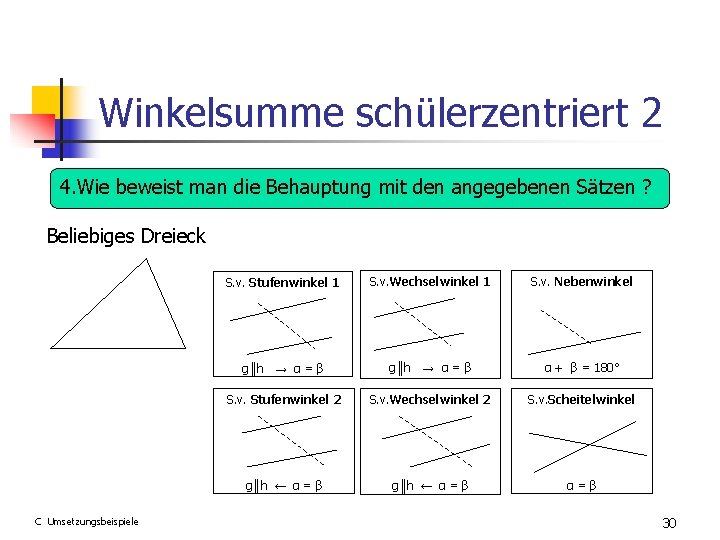
Winkelsumme schülerzentriert 2 4. Wie beweist man die Behauptung mit den angegebenen Sätzen ? Beliebiges Dreieck C Umsetzungsbeispiele S. v. Stufenwinkel 1 S. v. Wechselwinkel 1 S. v. Nebenwinkel g║h → α = β α + β = 180° S. v. Stufenwinkel 2 S. v. Wechselwinkel 2 S. v. Scheitelwinkel g║h ← α = β α=β 30

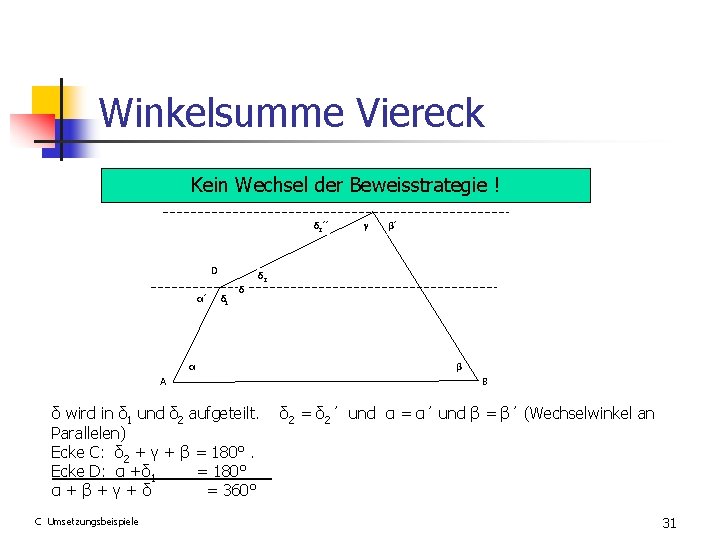
Winkelsumme Viereck Kein Wechsel der Beweisstrategie ! C δ 2´´ D α´ δ 1 δ β´ δ 2 α A δ wird in δ 1 und δ 2 aufgeteilt. Parallelen) Ecke C: δ 2 + γ + β = 180°. Ecke D: α +δ 1 = 180° α+β+γ+δ = 360° C Umsetzungsbeispiele γ β B δ 2 = δ 2´ und α = α´ und β = β´ (Wechselwinkel an 31

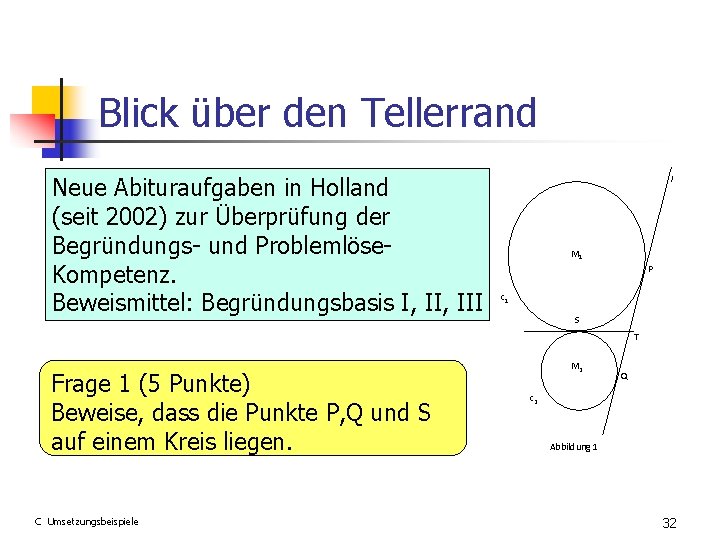
Blick über den Tellerrand Neue Abituraufgaben in Holland (seit 2002) zur Überprüfung der Begründungs- und Problemlöse. Kompetenz. Beweismittel: Begründungsbasis I, III l M 1 P c 1 S T Frage 1 (5 Punkte) Beweise, dass die Punkte P, Q und S auf einem Kreis liegen. C Umsetzungsbeispiele M 2 Q c 2 Abbildung 1 32

Fachkonferenz: Arbeitsauftrag (Vorschlag) 4 (Material S. 35 – 36) Bis zu welchem Niveau streben wir Aufgaben zur Begründungskompetenz und Problemlösekompetenz in Klassenarbeiten an ? Welche Aspekte sind für die Bewertung relevant ? 33

Logik-Lehrplan Bildungsplan 2004 (unter Begründen) elementare Regeln und Gesetze der Logik kennen und anwenden Begründungstypen und Beweismethoden der Mathematik kennen, gezielt auswählen und anwenden in mathematischen Kontexten Vermutungen entwickeln, formulieren und untersuchen. gleichartige Strukturen erkennen, verallgemeinern und spezialisieren D Logik-Lehrplan 34

Logik-Lehrplan 1 Der Schüler 1 a. weiß, dass ein math. Satz die Form „Wenn [A], dann [B] “ b. kann zwischen „für alle“ und „es gibt“ –Aussagen unterscheiden c. versteht den logischen Gehalt eines Satzes 2 a. kann zu einem Satz die Umkehrung bilden. b. weiß, dass von der Wahrheit eines Satzes nicht auf die Wahrheit der Umkehrung geschlossen werden kann. 3 a. kann den Umfang einer Definition bestimmen. b. kann zwischen Ober- und Unterbegriff unterscheiden. 4. kennt die Bedeutung eines Beispiels / eines Gegenbeispiels. 5. kann lokal deduktiv denken. D Logik-Lehrplan 35

Logik-Lehrplan 2 Das ist in der Schule kaum zu leisten: Der Schüler 6. kennt die Beweismethode der Kontraposition. 7. Kennt die Beweismethode „Beweis durch Widerspruch“. 8. kennt den Unterschied zwischen mathematischer Wahrheit und naturwissenschaftlicher Wahrheit D Logik-Lehrplan 36

Fachkonferenz: Arbeitsauftrag (Vorschlag) 5 (Material S. 37 – 40) Welche Aspekte eines Logik-Lehrplanes wollen wir im Mathematikunterricht fördern und einfordern ? Was erwarten wir jeweils in welcher Klassenstufe ? 37
 Kompetenzorientierter mathematikunterricht
Kompetenzorientierter mathematikunterricht Griff herausforderung
Griff herausforderung Lernprodukte
Lernprodukte Digitale medien im mathematikunterricht der grundschule
Digitale medien im mathematikunterricht der grundschule Rituale mathematikunterricht
Rituale mathematikunterricht Was ist eine funktion
Was ist eine funktion Perzeptive mengenbeurteilung
Perzeptive mengenbeurteilung Kognitive landkarte beispiel
Kognitive landkarte beispiel Kognitive triade
Kognitive triade Kognitive forenklingsstrategier
Kognitive forenklingsstrategier Vierte welle der verhaltenstherapie
Vierte welle der verhaltenstherapie De 7 kognitive evner
De 7 kognitive evner Dr. samuel pfeifer
Dr. samuel pfeifer Hva er kasusformulering
Hva er kasusformulering Die kommunikative methode
Die kommunikative methode Affektive lernziele
Affektive lernziele Læringsstile e-learning
Læringsstile e-learning Lernbereiche kognitiv
Lernbereiche kognitiv Depressiver grundkonflikt oral-regressive verarbeitung
Depressiver grundkonflikt oral-regressive verarbeitung Praktische anleitung über arbeitsblätter
Praktische anleitung über arbeitsblätter Den kognitive pyramide
Den kognitive pyramide Whiskysmagning holstebro
Whiskysmagning holstebro Kognitive grammatik langacker
Kognitive grammatik langacker Kognitive krav
Kognitive krav Perzeptive und kognitive mengenbeurteilung
Perzeptive und kognitive mengenbeurteilung Kognitive und kommunikative fähigkeiten beispiele
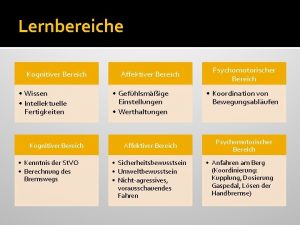
Kognitive und kommunikative fähigkeiten beispiele Lernbereiche
Lernbereiche Mesimdhenia interaktive
Mesimdhenia interaktive Ergonomie referat
Ergonomie referat Kognitive triade
Kognitive triade Dysfunktionale grundannahmen beispiele
Dysfunktionale grundannahmen beispiele Was ist eine wärmeströmung
Was ist eine wärmeströmung Glagoli vrste
Glagoli vrste Alle sind mitreisende im zug des lebens
Alle sind mitreisende im zug des lebens Was ist eine gruppe
Was ist eine gruppe Psychose
Psychose Was ist eine lebensmittelsicherheitskultur
Was ist eine lebensmittelsicherheitskultur Sucht hat immer eine geschichte
Sucht hat immer eine geschichte