Was ist eine Funktion Eine Zuordnung die jedem

Was ist eine Funktion? Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet

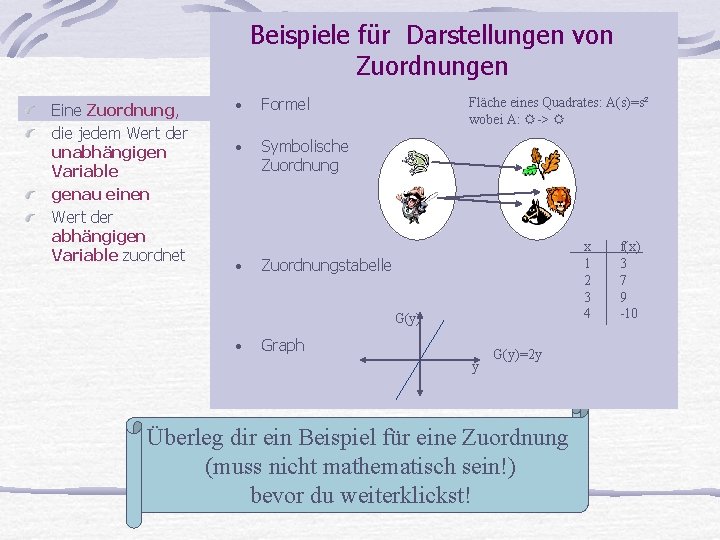
Beispiele für Darstellungen von Zuordnungen Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet • Formel • Symbolische Zuordnung • Fläche eines Quadrates: A(s)=s² wobei A: -> x 1 2 3 4 Zuordnungstabelle G(y) • Graph y G(y)=2 y Überleg dir ein Beispiel für eine Zuordnung (muss nicht mathematisch sein!) bevor du weiterklickst! f(x) 3 7 9 -10

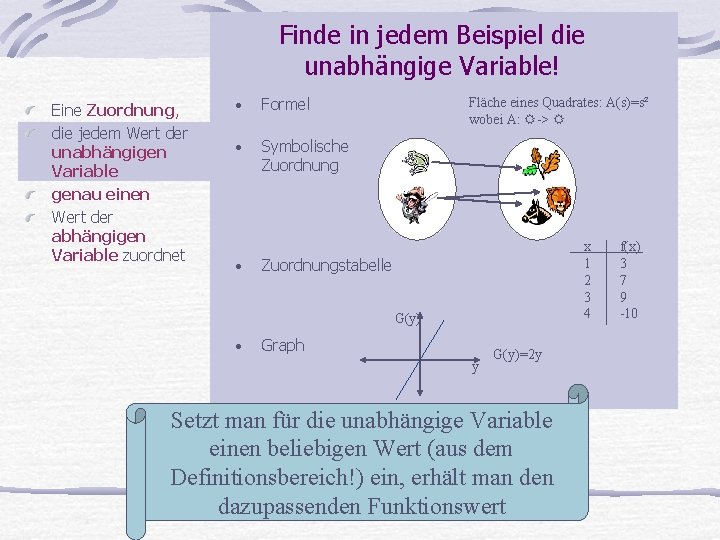
Finde in jedem Beispiel die unabhängige Variable! Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet • Formel • Symbolische Zuordnung • Fläche eines Quadrates: A(s)=s² wobei A: -> x 1 2 3 4 Zuordnungstabelle G(y) • Graph y G(y)=2 y Setzt man für die unabhängige Variable einen beliebigen Wert (aus dem Definitionsbereich!) ein, erhält man den dazupassenden Funktionswert f(x) 3 7 9 -10

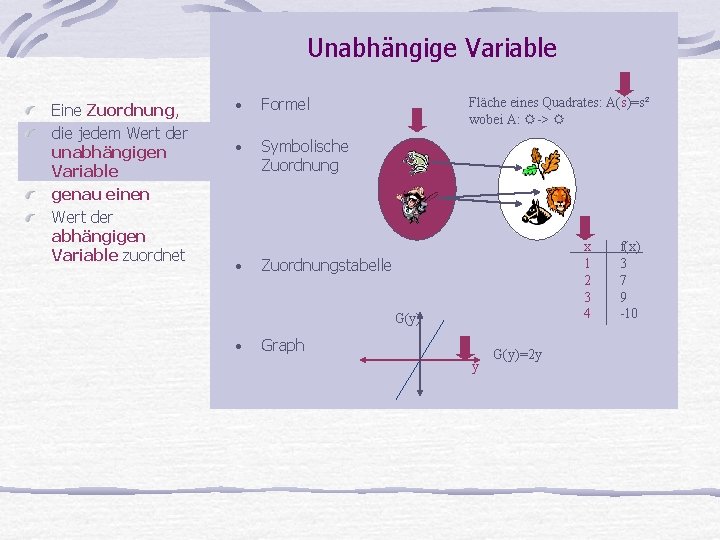
Unabhängige Variable Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet • Formel • Symbolische Zuordnung • Fläche eines Quadrates: A(s)=s² wobei A: -> x 1 2 3 4 Zuordnungstabelle G(y) • Graph y G(y)=2 y f(x) 3 7 9 -10

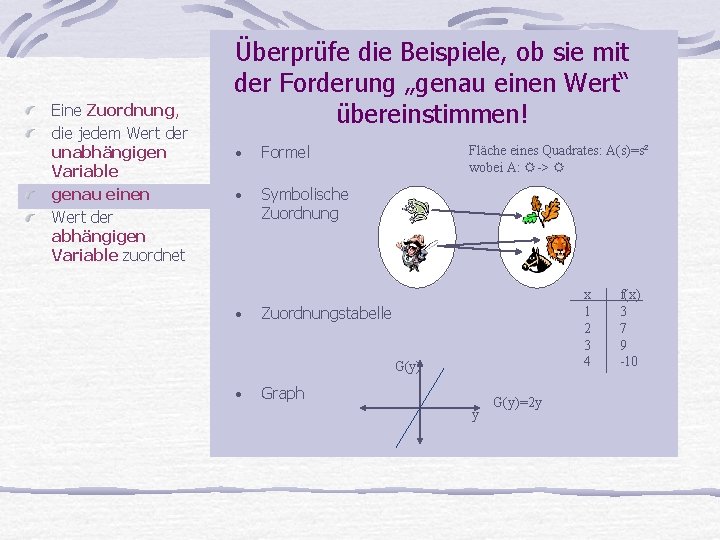
Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet Überprüfe die Beispiele, ob sie mit der Forderung „genau einen Wert“ übereinstimmen! • Formel • Symbolische Zuordnung • Fläche eines Quadrates: A(s)=s² wobei A: -> x 1 2 3 4 Zuordnungstabelle G(y) • Graph y G(y)=2 y f(x) 3 7 9 -10

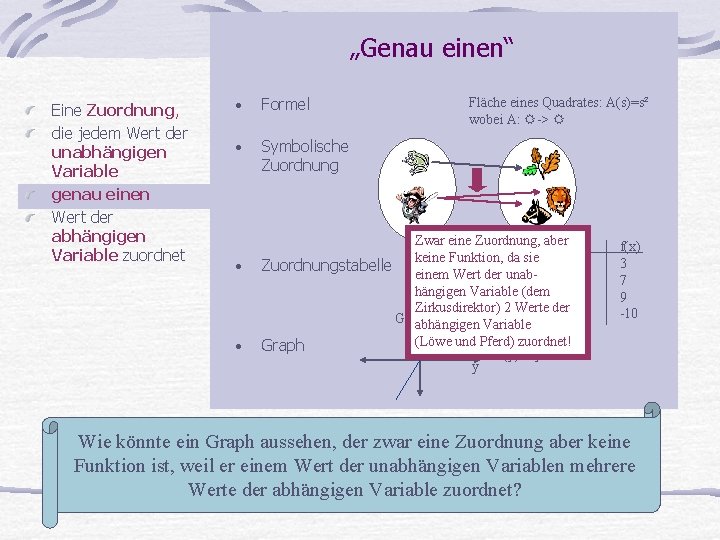
„Genau einen“ Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet • Formel • Symbolische Zuordnung • • Fläche eines Quadrates: A(s)=s² wobei A: -> Zwar eine Zuordnung, aber keine Funktion, da sie Zuordnungstabelle einem Wert der unabhängigen Variable (dem Zirkusdirektor) 2 Werte der G(y)abhängigen Variable (Löwe und Pferd) zuordnet! Graph G(y)=2 y y x 1 2 3 4 f(x) 3 7 9 -10 Wie könnte ein Graph aussehen, der zwar eine Zuordnung aber keine Funktion ist, weil er einem Wert der unabhängigen Variablen mehrere Werte der abhängigen Variable zuordnet?

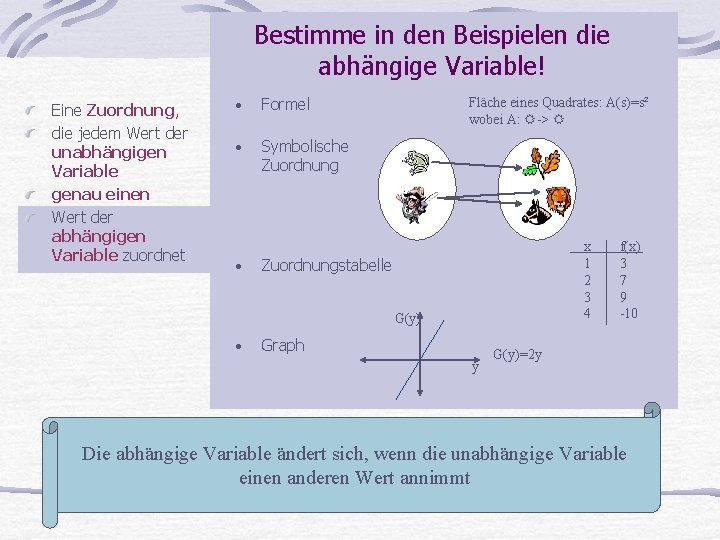
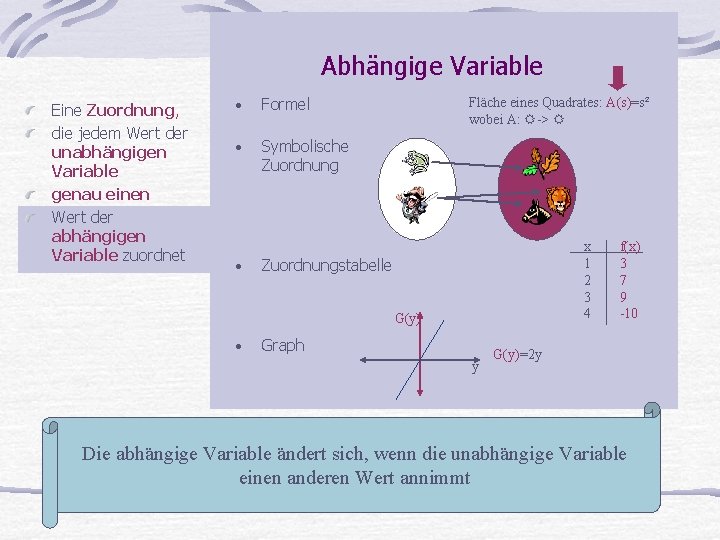
Bestimme in den Beispielen die abhängige Variable! Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet • Formel • Symbolische Zuordnung • Fläche eines Quadrates: A(s)=s² wobei A: -> x 1 2 3 4 Zuordnungstabelle G(y) • Graph y f(x) 3 7 9 -10 G(y)=2 y Die abhängige Variable ändert sich, wenn die unabhängige Variable einen anderen Wert annimmt

Abhängige Variable Eine Zuordnung, die jedem Wert der unabhängigen Variable genau einen Wert der abhängigen Variable zuordnet • Formel • Symbolische Zuordnung • Fläche eines Quadrates: A(s)=s² wobei A: -> x 1 2 3 4 Zuordnungstabelle G(y) • Graph y f(x) 3 7 9 -10 G(y)=2 y Die abhängige Variable ändert sich, wenn die unabhängige Variable einen anderen Wert annimmt

Beispiele Bestimme, ob es sich um eine Funktion handelt und welches die abhängige/unabhängige Variable ist: y=2 x+3 In diesem Beispiel treten 2 Variable auf, x und y. Leider ist nicht ersichtlich, welches die abhängige und welches die unabhängige ist. Aus der Schule weißt du, dass meist x für die unabhängige Variable verwendet wird. Um im Beispiel klar zu machen, dass es sich um eine Funktion handelt, müsste man schreiben: y(x)=2 x+3

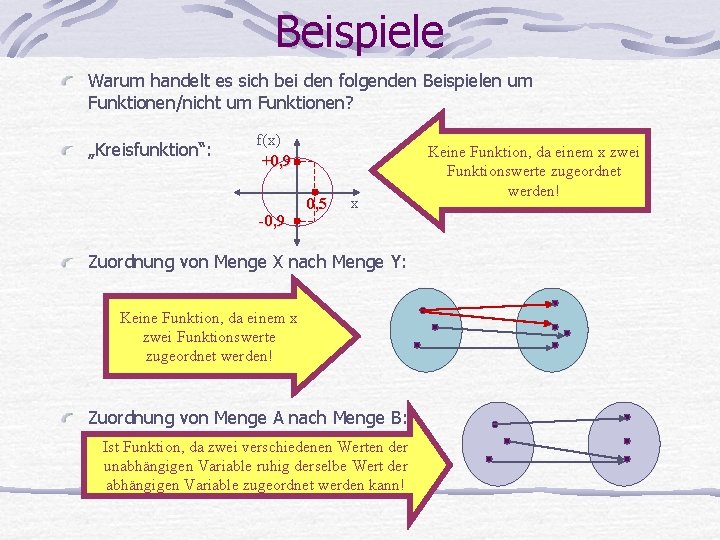
Beispiele Warum handelt es sich bei den folgenden Beispielen um Funktionen/nicht um Funktionen? „Kreisfunktion“: f(x) +0, 9 -0, 9 0, 5 x Zuordnung von Menge X nach Menge Y: Keine Funktion, da einem x zwei Funktionswerte zugeordnet werden! Zuordnung von Menge A nach Menge B: Ist Funktion, da zwei verschiedenen Werten der unabhängigen Variable ruhig derselbe Wert der abhängigen Variable zugeordnet werden kann! Keine Funktion, da einem x zwei Funktionswerte zugeordnet werden!