KELAS XI SEMESTER GENAP Standar Kompetensi Menggunakan konsep

KELAS XI SEMESTER GENAP

Standar Kompetensi Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah Kompetensi dasar Menggunakan turunan untuk menentukan karakteristik suatu fungsi dan memecahkan masalah. Indikator 1. Menentukan fungsi monoton naik dan turun dengan enggunakan konsep turunan pertama. 2. Menggambarkan sketsa grafik fungsi dengan menggunakan ifatsifat turunan. 3. Menentukan titik ekstrim grafik fungsi 4. Menentukan persamaan garis singgung dari sebuah fungsi.

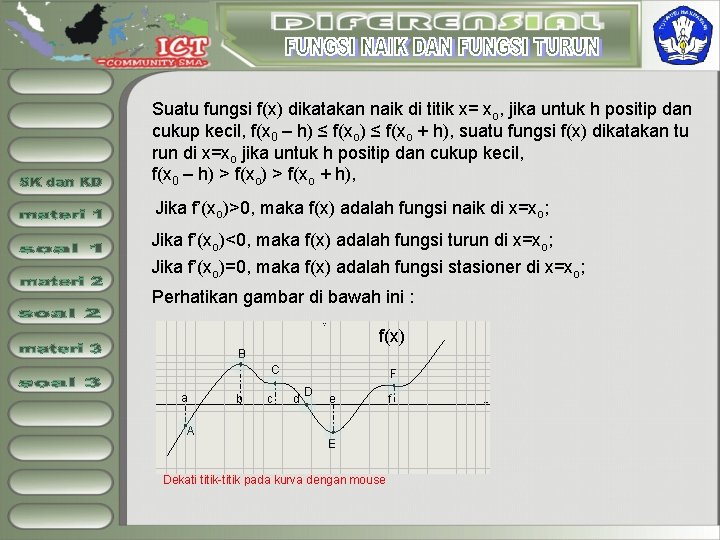
Suatu fungsi f(x) dikatakan naik di titik x= xo, jika untuk h positip dan cukup kecil, f(x 0 – h) ≤ f(xo + h), suatu fungsi f(x) dikatakan tu run di x=xo jika untuk h positip dan cukup kecil, f(x 0 – h) > f(xo + h), Jika f’(xo)>0, maka f(x) adalah fungsi naik di x=xo; Jika f’(xo)<0, maka f(x) adalah fungsi turun di x=xo; Jika f’(xo)=0, maka f(x) adalah fungsi stasioner di x=xo; Perhatikan gambar di bawah ini : f(x) B C a b c F d D e A E Dekati titik-titik pada kurva dengan mouse f

Suatu fungsi f(x) dikatakan naik di titik x= xo, jika untuk h positip dan cukup kecil, f(x 0 – h) ≤ f(xo + h), suatu fungsi f(x) dikatakan tu run di x=xo jika untuk h positip dan cukup kecil, f(x 0 – h) > f(xo + h), Jika f’(xo)>0, maka f(x) adalah fungsi naik di x=xo; Jika f’(xo)<0, maka f(x) adalah fungsi turun di x=xo; Jika f’(xo)=0, maka f(x) adalah fungsi stasioner di x=xo; Perhatikan gambar di bawah ini : f(x) B C a b c F d D e A E Dekati titik-titik pada kurva dengan mouse f Pada selang a<f(x)<b fungsi f(x) naik , di titik A garis singgung Pada kurva condong ke kanan (mempunyai Gradien positip), m=f ’(x)>0

Suatu fungsi f(x) dikatakan naik di titik x= xo, jika untuk h positip dan cukup kecil, f(x 0 – h) ≤ f(xo + h), suatu fungsi f(x) dikatakan tu run di x=xo jika untuk h positip dan cukup kecil, f(x 0 – h) > f(xo + h), Jika f’(xo)>0, maka f(x) adalah fungsi naik di x=xo; Jika f’(xo)<0, maka f(x) adalah fungsi turun di x=xo; Jika f’(xo)=0, maka f(x) adalah fungsi stasioner di x=xo; Perhatikan gambar di bawah ini : f(x) B C a b c F d D e A E Dekati titik-titik pada kurva dengan mouse f Pada titik B yaitu pada x=b fungsi f(x) stasioner , di titik B garis singgung Pada kurva sejajar sb. x (mempunyai Gradien nol), m=f ’(x)=0, Titik B disebut titik puncak

Suatu fungsi f(x) dikatakan naik di titik x= xo, jika untuk h positip dan cukup kecil, f(x 0 – h) ≤ f(xo + h), suatu fungsi f(x) dikatakan tu run di x=xo jika untuk h positip dan cukup kecil, f(x 0 – h) > f(xo + h), Jika f’(xo)>0, maka f(x) adalah fungsi naik di x=xo; Jika f’(xo)<0, maka f(x) adalah fungsi turun di x=xo; Jika f’(xo)=0, maka f(x) adalah fungsi stasioner di x=xo; Perhatikan gambar di bawah ini : f(x) B C a b c F d D e A E Dekati titik-titik pada kurva dengan mouse f Pada titik C yaitu pada x=c fungsi f(x) stasioner , di titik C garis singgung Pada kurva sejajar sb. x (mempunyai Gradien nol), m=f ’(x)=0, Titik C disebut titik belok

Suatu fungsi f(x) dikatakan naik di titik x= xo, jika untuk h positip dan cukup kecil, f(x 0 – h) ≤ f(xo + h), suatu fungsi f(x) dikatakan tu run di x=xo jika untuk h positip dan cukup kecil, f(x 0 – h) > f(xo + h), Jika f’(xo)>0, maka f(x) adalah fungsi naik di x=xo; Jika f’(xo)<0, maka f(x) adalah fungsi turun di x=xo; Jika f’(xo)=0, maka f(x) adalah fungsi stasioner di x=xo; Perhatikan gambar di bawah ini : f(x) B C a b c F d D e A E Dekati titik-titik pada kurva dengan mouse f Pada selang c<f(x)<e fungsi f(x) turun , di titik D garis singgung Pada kurva condong ke kiri (mempunyai Gradien negatip), m=f ’(x)<0

Suatu fungsi f(x) dikatakan naik di titik x= xo, jika untuk h positip dan cukup kecil, f(x 0 – h) ≤ f(xo + h), suatu fungsi f(x) dikatakan tu run di x=xo jika untuk h positip dan cukup kecil, f(x 0 – h) > f(xo + h), Jika f’(xo)>0, maka f(x) adalah fungsi naik di x=xo; Jika f’(xo)<0, maka f(x) adalah fungsi turun di x=xo; Jika f’(xo)=0, maka f(x) adalah fungsi stasioner di x=xo; Perhatikan gambar di bawah ini : f(x) B C a b c F d D e A E Dekati titik-titik pada kurva dengan mouse f Pada titik E yaitu pada x=e fungsi f(x) stasioner , di titik E garis singgung Pada kurva sejajar sb. x (mempunyai Gradien nol), m=f ’(x)=0, Titik E disebut titik puncak

Suatu fungsi f(x) dikatakan naik di titik x= xo, jika untuk h positip dan cukup kecil, f(x 0 – h) ≤ f(xo + h), suatu fungsi f(x) dikatakan tu run di x=xo jika untuk h positip dan cukup kecil, f(x 0 – h) > f(xo + h), Jika f’(xo)>0, maka f(x) adalah fungsi naik di x=xo; Jika f’(xo)<0, maka f(x) adalah fungsi turun di x=xo; Jika f’(xo)=0, maka f(x) adalah fungsi stasioner di x=xo; Perhatikan gambar di bawah ini : f(x) B C a b c F d D e A E Dekati titik-titik pada kurva dengan mouse f Pada titik F yaitu pada x=f fungsi f(x) stasioner , di titik F garis singgung Pada kurva sejajar sb. x (mempunyai Gradien nol), m=f ’(x)=0, Titik F disebut titik belok

Contoh Soal : Selidikilah fungsi di bawah ini termasuk fungsi naik, fungsi stasioner atau fungsi turun pada titik yang ditentukan 1. Y = 3 x 2 + x -2 2. Y = x 3 - 2 x 2 - 1 3. Y = ½. x 4 - 4 x 2 - 7 4. Y = sin 2 x + cos x di titik x= 4 di titik x= 1 di titik x = ½ Jawab. 1. y = 3 x 2 + x -2 di titik x= 4 y ’ = 6 x + 1 y ‘ = 25 > 0 karena y ‘ > 0 maka fungsi di titik x = 4 merupakan fungsi naik 2. Y = x 3 - 2 x 2 - 1 di titik x= 1 y ’= 3 x 2 - 4 x y ‘ = -1 < 0 karena y ‘ < 0 maka fungsi di titik x = 1 merupakan fungsi turun

Jawab. 3. y = ½. x 4 - 4 x 2 - 7 di titik x= 2 4. Y = sin 2 x + cos x di titik x = ½ y ’= 2 cos 2 x – sin x y ’ = 2 x 3 - 8 x y ‘= -3 < 0 y‘=0 karena y ‘ < 0 maka fungsi di karena y ‘ = 0 maka fungsi di titik x = 1 merupakan fungsi titik x = 2 merupakan fungsi turun stasioner Latihan soal : Selidikilah fungsi di bawah ini termasuk fungsi naik, fungsi stasioner atau fungsi turun pada titik yang ditentukan 1. y = 5 x 2 + x - 7 di titik x= 1 2. Y = 2 x 3 - 5 x 2 - 1 di titik x= 1 3. Y = 2. x 4 - 4 x 3 - 7 di titik x= 1 4. Y = cos 2 x + sin x di titik x = ½

Pengujian turunan pertama : 1. Pecahkan f ’(x)= 0 untuk mendapatkan harga kritis 2. Gambarkan harga kritis tersebut pada garis bilangan, dengandemikian terbentuk sejumlah selang 3. Tentukan tanda f ‘ (x) pada tiap selang 4. Misalkan x bertambah setelah tiap harga kritis x=xo; maka f(x) mempunyai harga maksimum (=f(xo) jika f ‘ (x) berubah dari + ke f(x) mempunyai harga minimum (=f(xo) jika f ‘ (x) berubah dari – ke + f(x) tidak mempunyai harga maksimum maupun minimum di (x=xo) jika f ‘ (x) tidak mengalami perubahan tanda

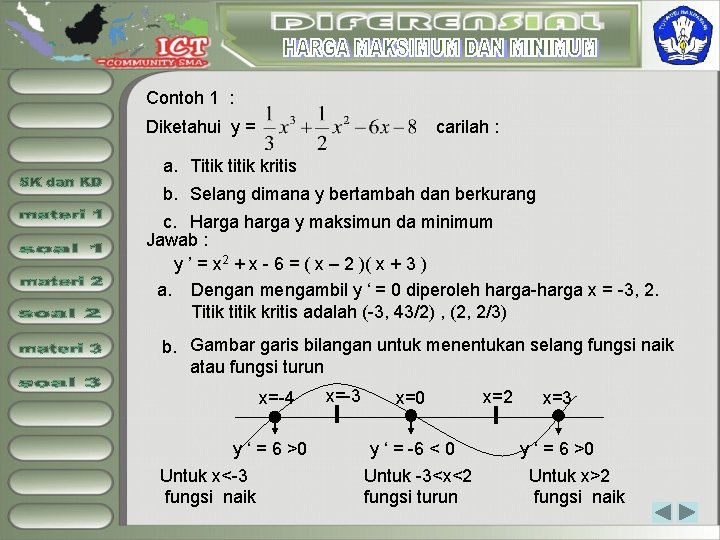
Contoh 1 : Diketahui y = carilah : a. Titik titik kritis b. Selang dimana y bertambah dan berkurang c. Harga harga y maksimun da minimum Jawab : y ’ = x 2 + x - 6 = ( x – 2 )( x + 3 ) a. Dengan mengambil y ‘ = 0 diperoleh harga-harga x = -3, 2. Titik titik kritis adalah (-3, 43/2) , (2, 2/3) b. Gambar garis bilangan untuk menentukan selang fungsi naik atau fungsi turun x=-4 y ‘ = 6 >0 Untuk x<-3 fungsi naik x=-3 x=0 y ‘ = -6 < 0 Untuk -3<x<2 fungsi turun x=2 x=3 y ‘ = 6 >0 Untuk x>2 fungsi naik

Jawab : y = c. Untuk y ‘= 0 maka f(p) disebut nilai stasioner dari f pada x=p y ‘ = 0 untuk x = -3 dan x = 2 Substitusikan nilai x = -3 dan x = 2 pada fungsi : y= Untuk x = -3 maka nilai stasioner y = 43/2 f ‘(x) berubah dari + menuju - menunjukkan nilai stasioner tersebut merupakan nilai maksimum relatif Untuk x = 2 maka nilai stasioner y = 2/3 f ‘(x) berubah dari - menuju + menunjukkan nilai stasioner tersebut merupakan nilai minimum relatif

Jawab : y = sin x + cos x c. Untuk y ‘= 0 maka f(p) disebut nilai stasioner dari f pada x=p y ‘ = 0 untuk x = dan x = Substitusikan nilai x = dan x = pada fungsi : y = sin x + cos x Untuk x = maka nilai stasioner y = f ‘(x) berubah dari + menuju - menunjukkan nilai stasioner tersebut merupakan nilai maksimum relatif Untuk x = maka nilai stasioner y = f ‘(x) berubah dari - menuju + menunjukkan nilai stasioner tersebut merupakan nilai minimum relatif

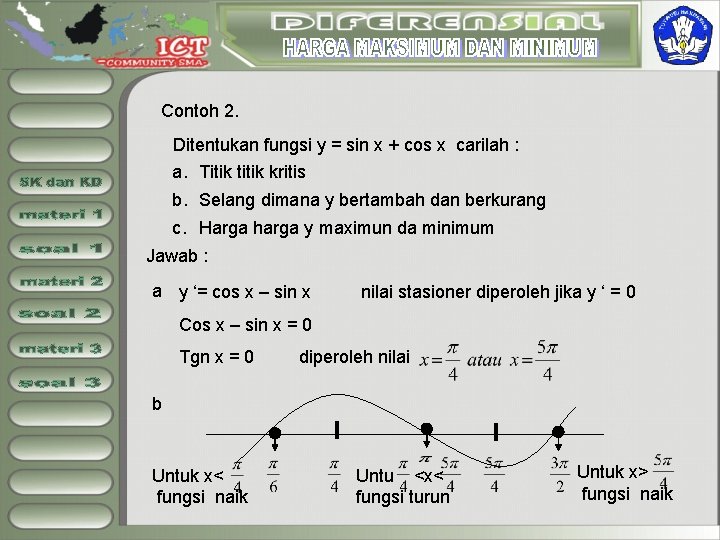
Contoh 2. Ditentukan fungsi y = sin x + cos x carilah : a. Titik titik kritis b. Selang dimana y bertambah dan berkurang c. Harga harga y maximun da minimum Jawab : a y ‘= cos x – sin x nilai stasioner diperoleh jika y ‘ = 0 Cos x – sin x = 0 Tgn x = 0 diperoleh nilai b Untuk x< fungsi naik Untu <x< fungsi turun Untuk x> fungsi naik

Tentukan : a. Titik titik kritis b. Selang dimana y bertambah dan berkurang c. Harga harga y maksimun da minimum Untuk fungsi dibawah ini : a. y = x 2 – 4 x e. y = ( 2 – x )3 b. y = f. y = (x-4)4(x-3)3 c. y = g. y = d. y = x 4 + 2 x 3 -3 x 2 -4 x + 4 h. y = cos 2 x untuk ½ ≤ x ≤ 3/2

Contoh soal : Dengan menggunakan pagar kawat sepanjang 200 m akan dibangun suatu kandang ayam yang bentuknya persegi panjang, tentukan ukuran kandang agar luas kandang maksimum Jawab. Keliling kandang = 2 P + 2 L = 200 P + L = 100 P = 100 - L Luas kandang = p x L Luas = P. L Luas = ( 100 – L). L Luas = 100 L – L 2 Nilai stasioner dicari dengan Luas ‘ = 0 Luas ‘ = 100 – 2 L = 0 2 L = 100 L = 50 50 40 60 Luas ‘ = 100 – 2. 40 Luas ‘ = 100 – 2. 60 = 20 > 0 = -20 < 0 Untuk L = 50 maka nilai stasioner y = 50 x 50 = 2500 Luas ‘ berubah dari + menuju - menunjukkan nilai stasioner tersebut merupakan nilai maksimum

Contoh soal : Jumlah dua bilangan adalah 30, tentukan kedua bilangan tersebut agar hasil kalinya maksimum Jawab. Misal bilangan tersebut a dan b maka a + b = 30; a = 30 – b, misal Hasil kali kedua bilangan = P P =axb = (30 – b)xb = 30 b – b 2 Nilai stasioner jika P’ = 0 10 P’ = 30 – 2 b = 0 2 b = 30 P’ = 30 – 2 b b = 15 P’ = 10 15 20 P’ = 30 – 2 b P’ = -10 Untuk b = 15 maka nilai stasioner y = 15 x 15 = 225 hasil kali antara a dan b berubah dari + menuju - menunjukkan nilai stasioner tersebut merupakan nilai maksimum

Soal Latihan : 1. Dari suatu karton persegi panjang yang sisinya 24 cm, akan dibuat suatu kotak tanpa tutup dengan jalan memotong pada keempat sudut persegi panjang tersebut dengan sisi x cm tentukan x agar sisi kotak maksimum. 2. Segitiga siku AOB terbentuk dari sumbu X, sumbu Y, dan sisi AB dengan persamaan y = 10 – 2 x. Dari titik C(x, y) yang terletak pada AB, dibuat garis tegak lurus sumbu koordinat sehingga terjadi persegi panjang dengan diagonal OC. 3. Jumlah dua bilangan adalah 40. tentukan masing bilangan tersebut agar hasil kali antara bilangan yang satu dengan kuadrat yang lainnya maksimum. 4. Suatu kotak tanpa tutup dengan alas persegi berisi x cm dan tinggi t cm. isi kotak tersebut 2. 000 cm 3. tentukan ukuran kotak agar bahan untuk membuat kotak minimum. ( cari luas permukaan kotak minimum). 5. Suatu tangki air berbentuk silinder lingkaran tegak dengan diameter alasnya 1 m. apabila tinggi air dalam tangki x cm, tentukan laju perubahan volume v terhadap penambahan tinggi x, ketika air diisikan ke dalam tangki tersebut