KELAS XI SEMESTER GENAP Standar Kompetensi Menggunakan konsep

KELAS XI SEMESTER GENAP

Standar Kompetensi Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah Kompetensi dasar Menggunakan konsep dan aturan turunan dalam perhitungan turunan fungsi Indikator 1. Menghitung fungsi yang mengarah ke konsep turunan 2. Menjelaskan arti fisis (sebagai laju perubahan) dan arti geometri turunan di satu titik. 3. Menghitung turunan fungsi yang sederhana dengan menggu nakan defenisi turunan. 4. Menentukan sifat-sifat turunan fungsi 5. Menentukan turunan fungsi aljabar dan trigonometri dengan menggunakan sifat-sifat turunan 6. Menentukan turunan fungsi komposisi dengan aturan rantai

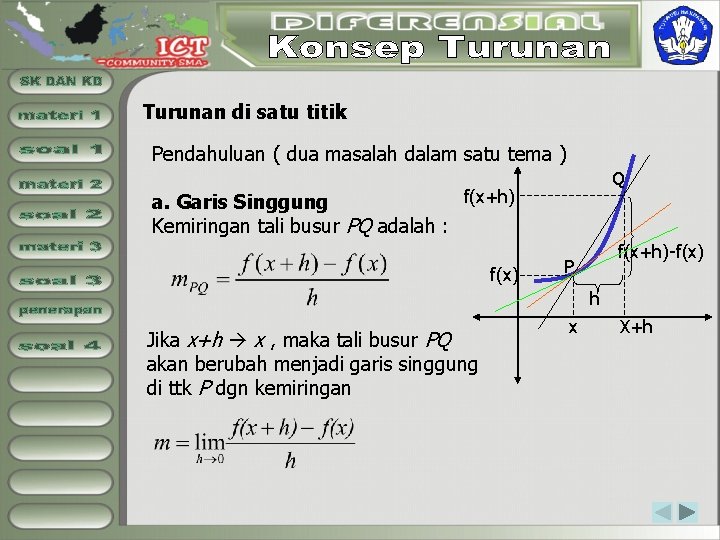
Turunan di satu titik Pendahuluan ( dua masalah dalam satu tema ) Q f(x+h) a. Garis Singgung Kemiringan tali busur PQ adalah : f(x) f(x+h)-f(x) P h Jika x+h x , maka tali busur PQ akan berubah menjadi garis singgung di ttk P dgn kemiringan x X+h

• b. Kecepatan Sesaat Misal sebuah benda bergerak sepanjang garis koordinat sehingga posisinya setiap saat diberikan oleh s = f(t). Pada saat t = c benda berada di f(c) dan saat t = c + h benda berada di f(c+h). Perubahan waktu c c+h Perubahan posisi f(c) f(c+h) s • Sehingga kecepatan rata-rata pada selang waktu [c, c+h] adalah

Jika h 0, diperoleh kecepatan sesaat di x = c : Untuk kecepatan sesaat di sembarang tempat dapat Dituliskan sebagai berikut Dari dua bentuk diatas : kemiringan garis singgung dan kecepatan sesaat terlihat bahwa dua masalah tersebut berada dalam satu tema, yaitu turunan : Definisi : Turunan pertama fungsi f(x) dinotasikan dengan lambang f’(x) dan didefinisikan sebagai berikut :

Notasi dari turunan fungsi f(x) : Contoh : Diketahui f(x) -. f(x) = C Jawab : f’(x) = -. f(x) = x 2 Jawab : f’(x) = tentukan f’(x) jika :

-. f(x) = x 3 Jawab : f’(x) = -. f(x) = xn Jawab : f’(x) =

Secara umum dapat dirumuskan jika : Untuk :

Contoh Soal : Tentukan turunan dari f(x) jika : a. f(x) = 2 x 2 + 3 x - 5 b. f(x) = Jawab : a. f(x) = 2 x 2 + 3 x - 5 f’(x) = 4 x + 3 b. f(x) = 3 – 4 x-3 +5 x-2

Soal Tentukan Turunan dari fungsi f(x) di bawah ini : 1. f(x) = 5 x 4 +2 x 2 -3 x +6 2. f(x) = 2 x 7 + 5 x 3. f(x) = 3 x-2 + 4 x-3 + 4 4. f(x) = 5. f(x) = ( 2 x + 3 )2 6. f(x) = 7. f(x) =

Dengan menggunakan definisi tersebut dapat diturunkan aturan untuk mencari turunan sebagai berikut : 1. 2. 3. dengan g(x) ≠ 0.

Bukti aturan ke-2 Misal u(x) = f(x). g(x)

Contoh 1. Tentukan turunan pertama dari Jawab : 2. Tentukan turunan pertama dari Jawab : 3. Tentukan turunan pertama dari Jawab :

Tentukan fungsi turunan pertama dari 1. 2. 3. 4. 5.

Perhatikan gambar di samping. Misalkan = AOB adalah sudut pusat lingkaran dengan jari =1. Sektor COD ≤▲COB ≤ sektor AOB Sehingga ½ cos 2 ≤ ½ sin cos ≤ ½ . 1 Bagi dengan ½ cos > 0 diperoleh; O Jika → 0 maka cos → 1 sehingga : Sehingga : B D OC= cos ; CB= sin A C

Bukti: a. Misal f(x) = sin x maka

b. Misal f(x) = cos x maka

Untuk turunan fungsi trigonometri yang lain dapat diperoleh Dengan menerapkan rumus perhitungan turunan, khususnya turunan bentuk u/v

Soal Latihan Tentukan turunan dari fungsi f(x) berikut ini : a. f(x) = sin 3 x + cos 2 x b. f(x) = x 2 sin 2 x c. f(x) = sin 2 x d. f(x) = 3 cos 2 x e. f(x) = tgn x f. f(x) = tgn 2 x g. f(x) = ½ tan x sin 2 x

Andaikan y = f(u) dan u = g(x). Jika Contoh 1: Tentukan dari Jawab : sehingga bentuk diatas menjadi Misal : Karena dan maka ada ,

Jika f(x)= un maka f’(x)=nu’un-1 Contoh 2 : Tentukan turunan dari : y = (3 x 2+4)4 Jawab : Misal u=(3 x 2+4) maka Dan y= u 4 maka sehingga : = 6 x. 4 u 3 = 6 x. 4(3 x 2+4)3 = 24 x. (3 x 2+4)3 Turunan dari y = (3 x 2+4)4 adalah y’= 24 x. (3 x 2+4)3

Jika y = f(u), u = g(v), v = h(x), dan Contoh 3: Tentukan dari Jawab : Misal u = Sin v sehingga Ada, maka

A. Tentukan fungsi turunan pertama dari 1. 2. 3. 4. 5. 6. y = sin x tan [ x 2 + 1 ] B. Tentukan turunan kedua dari 1. 3. 2. 4.

Untuk menentukan persamaan garis singgung pada kurva. Telah disinggung didepan bahwa gradien garis singgung pada suatu Kurva f(x) adalah turunan pertama dari fungsi terebut : m = f’(x) = Contoh Soal: Tentukan nilai gradien garis singgung pada kurva : a. y = x 2 -3 x +4 b. y = sin x Jawab : a. y = x 2 -3 x +4 b. y = sin x di titik A. ( 2, 2 ) untuk x = gradien m = y’ = 2 x – 3 di titik ( 2, 2 ) m = y’ = 2. 2 – 3 = 1 gradien m = y’ = cos x untuk x = m = cos =½

Pemakaian Gradien untuk menentukan persamaan garis singgung Terhadap suatu kurva di titik tertentu. Misalkan titik P(x 1, y 1) terletak pada kurfa f(x), maka persamaan Garis singgung yang melalui titik P pada kurva f(x) dituliskan sbb: Y – y 1 = f’(x) ( x – x 1) Contoh soal : Tentukan persamaan garis singgung pada kurva f(x) = x 3 – 2 x + 3 Dititik P(2, 7). Jawab : Gradien garis singgung = m = f’(x) = 3 x 2 – 2 di titik ( 2, 7) maka m = f’(x) = 10 Persamaan garis singgungnya , Y – y 1 = f’(x)(x-x 1) yaitu y – 7 = 10 ( x – 2 ) y – 7 = 10 x – 20 y = 20 x - 13

Jika l 1 garis yang memiliki gradien m 1; dan l 2 garis yang memiliki Gradien m 2, maka hubungan antara m 1 dan m 2 terhadap kedudukan Garis l 1 dan l 2 adalah sebagai berikut : Jika l 1 sejajar l 2 maka nilai m 1 = m 2 dan Jika l 1 tegak lurus l 2 maka nilai m 1. m 2 = -1 Contoh soal : Tentukan persamaan garis singgung pada kurva f(x) = x 2 – 3 x + 2 Yang sejajar terhadap garis y= 3 x + 4 Jawab : Gradien garis singgung = m = f’(x) = 2 x – 3 sejajar garis y = 3 x + 4 m 1 = m 2 = 3 maka 2 x – 3 = 3 ; x = 3 untuk x = 3 nilai y = 32 – 3. 3 + 2 = 2 maka titik singgungnya di ( 3, 2) Persamaan garis singgung yang ditanyakan adalah : Y– 2=3(x– 3) Y = 3 x – 11

Selain digunakan untuk menentukan gradien garis singgung, turunan Juga digunakan untuk menentukan kelajuan. Jika suau variabel x ada lah fungsi dari waktu laju perubahan x terhadap waktu dinyatakan Dalam dx/dt. Contoh soal : Mobil meluncur dengan membentuk fungsi S = 50 – 3 t – 2 t 2, tentukan Kecepatan mobil saat t=3. Jawab. Kecepatan = v = d. S/dt = -3 – 4 t Maka v = -3 -4. 3 = - 15 saat t=3

Contoh soal : Air mengalir keluar dari corong kerucut dengan kelajuan 5 cm 3 s-1 Jari-jari dasar corong adalah 10 cm dan tingginya 20 cm. hitung kelajuan air saat ketinggian air turun berjarak 5 cm dari puncak. Segitiga OAB sebangun dengan segitiga OCD maka r/10 = h/20 sehingga r = ½ h Karena r = ½ h maka Diketahui dv/dt = 5 cm 3 s-1 Air berjarak 5 cm dari puncak Maka air telah turun sejauh h = 20 – 5 = 15 cm B A 10 20 C r D h O Maka kelajuan air yang ditanyakan adalah : cm 3 s-1

SOAL LATIHAN 1. Tentukan persamaan garis singgung pada kurva f(x)= x 4 + 12 x – 5 1. Di titik ( 1, 11) 2. Tentukan persamaan garis singgung pada kurva f(x) = 2 x 3 - 23 x – 2 1. Yang sejajar dengan garis y = x - 7 3. Tentukan pesamaan garis singgung pada kurva f(x) = x 2 – 6 x + 4 Yang tegak lurus dengan garis y= ½ x - 5 4. Tentukan persamaan garis singgung pada lingkaran berpusat di (0, 0) 1. yang berjari 5 dan melalui titik P(3, 4). 5. Sebuah beban w diikatkan pada tali sepanjang 15 m, yang melewati 1. Katrol di p berjarak 6 m di atas tanah, ujung lain diikatkan pada truk 2. Dengan jarak 0. 5 m dari atas tanah, jika truk bergerak dengan kela 3. Juan 3 ms-s, berapa cepat beban naik jika beban berada 2 m diatas 4. Tanah? Perhatikan gambar dibawah ini. 9 -x 6 -x y x 0. 5