KARMAIK SAYILAR KARMAIK SAYININ TANIMI nin KUVVETLER K

KARMAŞIK SAYILAR

KARMAŞIK SAYININ TANIMI İ’nin KUVVETLERİ İKİ KARMAŞIK SAYININ EŞİTLİĞİ İKİ KARMAŞIK SAYININ EŞLENİĞİ KARMAŞIK SAYILARDA DÖRT İŞLEM KARMAŞIK DÜZLEM VE BİR KARMAŞIK SAYININ GÖRÜNTÜSÜ BİR KARMAŞIK SAYININ MUTLAK DEĞERİ (MODÜLÜ) KARMAŞIK SAYILARIN KUTUPSAL GÖSTERİMİ BİR KARMAŞIK SAYININ KUVVETİ BİR KARMAŞIK SAYININ KÖKLERİ

A. Tanım ax 2 + bx + c = 0 denkleminin < 0 iken reel kökünün olmadığını daha önce ortaya koymuştuk. Mesela x 2 + 1= 0 denkleminin reel kökü yoktur. Çünkü (x 2 + 1 = 0 x 2 = -1 ) karesi -1 olan reel sayı yoktur. Şimdi, bu türden denklemlerin çözümünü mümkün kılan ve reel sayılar kümesini de kapsayan yeni bir küme tanımlayacağız. Ø a ve b birer reel sayı ve i = olmak üzere z = a + bi şeklinde ifade edilen z sayısına karmaşık ( kompleks) sayı denir. Karmaşık sayılar kümesi C ile gösterilir. C= Ø z = a + bi karmaşık sayısında a ya karmaşık sayının reel ( gerçel) kısmı, b ye karmaşık sayının imajiner (sanal) kısmı denir ve Re(z) = a, İm(z)=b şeklinde gösterilir. Örnek. . . 1 sayıları birer karmaşık sayıdır. Re(z 1) = 2 ve İm(z 1) = -3 tür. Re(z 2) = ve İm(z 2) = -1 dir. Re(z 3) = -2 ve İm(z 3) = 0 dır. Re(z 4) = 0 ve İm(z 4) = 3 tür.

B. i nin Kuvvetleri i 0 = 1 i 1 = i n N olmak üzere i 2 = -1 i 3 = -i i 4 n = 1 i 4 n+1 = i i 5 = i Görüldüğü gibi i nin kuvvetleri ; 1, i, -1, -i değerlerinden birine eşit olmaktadır. i 4 n+2 = -1 i 4 n+3 = -i dir. Örnek. . . 2 84 = 4. 21 olduğu için i 84 = 1, 61 = 4. 15 + 1 olduğu için i 61 = i, 98 = 4. 24 + 2 olduğu için i 98 = -1 47 = 4. 11 + 3 olduğu için i 47 = -i dir. Örnek. . . 3 i 2 = -1 olmak üzere i 20= (i 4)5 = 1 , i 21= (i 4)5. i = i ve (1+ i 20). (1+ i 21). (1+ i 22) çarpımı aşağıdakilerden hangisine eşittir? A) -i B) -1 C) 0 Çözüm D) 1 E) i i 22= (i 4)5. i 2 = 1. (-1) = -1 olduğu için, (1+ i 20). (1+ i 21). (1+ i 22) = (1 + 1). (1+ i). (1 – 1) = 2. (1 + i). 0 = 0 olur.

C. İki Karmaşık Sayının Eşitliği Reel kısımları ve imajiner kısımları kendi aralarında eşit olan iki karmaşık sayı eşittir. Örnek. . . 4 A) -2 B) -1 C) 2 D) 3 E) 5 Çözüm Cevap D

D. Bir Karmaşık Sayının Eşleniği Örnek. . . 5 Reel katsayılı ax 2+bx+c=0 ikinci dereceden denkleminin köklerinden biri z=m+ni karmaşık sayısı ise diğeri bu kökün eşleniği olan z=m-ni sayısıdır. Örnek. . . 6 Çözüm x 2 - 2 x + 5 = 0 denkleminin çözüm kümesini bulalım. Verilen denklemde a = 1, b = -2, c = 5 tir.

E. Karmaşık Sayılarda Dört İşlem 1. Toplama - Çıkarma Karmaşık sayılar toplanırken ya da çıkarılırken reel ve sanal kısımlar kendi aralarında toplanır ya da çıkarılır. Örnek. . . 7 2. Çarpma Karmaşık sayılarda çarpma işlemi, i 2 = -1 olduğu göz önüne alınarak, reel sayılardakine benzer şekilde yapılır.

Örnek. . . 8 1. 3. 2. Çözüm 1. 3. 2. Örnek. . . 9 A) 125 B) 64 C) 27 D) 8 i Çözüm Cevap A E) 4 i

3. Bölme Karmaşık sayılarda bölme işlemi, paydanın eşleniği ile pay ve paydanın çarpılmasıyla sonuçlandırılır. Örnek. . . 10 Örnek. . . 11 z=a+bi sayısının, toplama işlemine göre tersi : -z = - a – bi çarpma işlemine göre tersi : Çözüm

F. Karmaşık Düzlem ve Bir Karmaşık Sayının Görüntüsü Ø İki boyutlu analitik düzlemdeki x ekseninin reel eksen, y ekseninin imajiner eksen alınmasıyla oluşturulan düzleme karmaşık düzlem denir. Ø z = a + bi karmaşık sayısının karmaşık düzlemdeki görüntüsü M(a, b) noktasıdır. Ø z = a + bi kompleks sayısının iki boyutlu vektör uzayındaki görüntüsü M = (a, b) olmak üzere OM vektörüdür. Örnek. . . 12 1. 2. İmajiner Eksen 2 O y z = 3+2 i. 3 Reel Eksen 2 z =. 3+2 i O 3 x

G. Bir Karmaşık Sayının Mutlak Değeri (Modülü) y Karmaşık düzlemde, bir karmaşık sayıya karşılık gelen noktanın başlangıç noktasına uzaklığına mutlak değeri (modülü) denir ve Iz. I şeklinde gösterilir. z =. a+bi b Iz. I O Iz. I Örnek. . . 13 z = 4 + 3 i sayısının mutlak değerini bularak karmaşık düzlemde gösterelim. Çözüm y z =. 4+3 i 3 5 Iz. I= O 4 x a x

H. Mutlak Değerle İlgili Özellikler Örnek. . . 14 A) 1 B) C) D) 2 E) 5 Çözüm Cevap A

Örnek. . . 15 A) – 4 -3 i Çözüm B) – 3 -4 i Cevap C C) – 4+3 i D) 3+4 i E) 4+3 i

Ø z 1= x 1+ iy 1 ve z 2= x 2+ iy 2 sayıları arasındaki uzaklık, bu sayıların karmaşık düzlemdeki görüntüleri olan noktalar arasındaki uzaklığa eşittir. Yani, Ø Iz-z 0 I = r şartını sağlayan z karmaşık sayılarının kümesi, z 0 sabit noktasına r birim uzaklıktaki noktaların kümesidir. Bu küme, merkezi z 0 ve yarıçapı r olan çemberdir. Ø Iz-z 0 I < r ifadesi merkezi z 0, yarıçapı r olan çemberin iç bölgesindeki noktaların kümesini gösterir. Ø Iz-z 0 I > r ifadesi merkezi z 0, yarıçapı r olan çemberin dış bölgesindeki noktaların kümesini gösterir. Örnek. . . 16 A) 5 B) 6 C) 8 D) 10 Çözüm Cevap D E) 13

A. Karmaşık Sayıların Kutupsal Gösterimi y M(a, b). b Iz. I O H a x Ø Yukarıda ifade edilen eşitlikleri sağlayan reel sayısına z nin argümenti denir ve arg(z) = şeklinde gösterilir. 0 2 ise ya karmaşık sayının esas argümenti denir. Ø Karmaşık sayının mutlak değer ve argümentine bu sayının kutupsal koordinatları denir ve (Iz. I, ) şeklinde gösterilir. Ø z= Iz. I. (cos +i. sin ) sayısı z=Iz. I. cis şeklinde de yazılabilir.

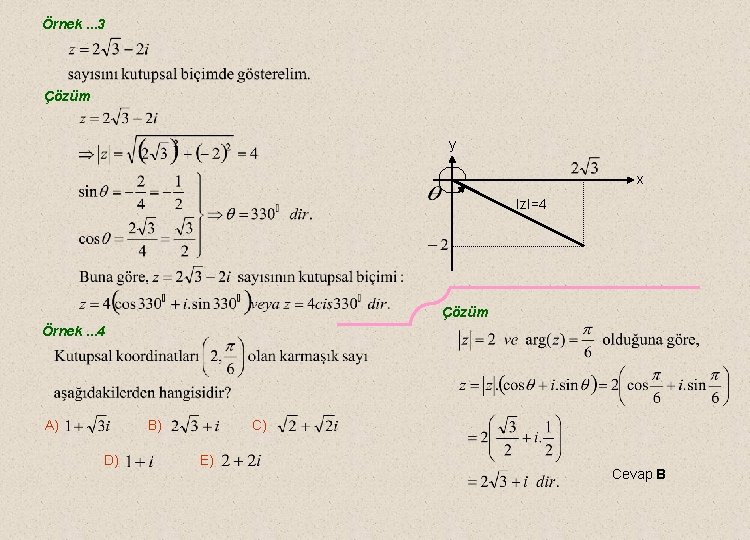
Örnek. . . 3 Çözüm y x Iz. I=4 Çözüm Örnek. . . 4 A) B) D) C) E) Cevap B

1. 2. 3. Örnek. . . 5 A) B) C) D) E) Çözüm Cevap D

Örnek. . . 6 A) B) C) D) E) Çözüm Cevap B y P M x

B. Kutupsal Biçimde İşlemler Örnek. . . 7 Çözüm

C. Bir Karmaşık Sayının Kuvveti Örnek. . . 8 A)-64 i B)32 C)32 i D)64 E)64 i Çözüm Cevap E

Örnek. . . 9 A) Çözüm B) C) D) E) Cevap A Örnek. . . 10 A) -i B) -1 C) D)i E)1 Çözüm Cevap E

D. Bir Karmaşık Sayının Kökleri Ø Ø Örnek. . . 11 Çözüm