Grunnskolelrerutdanningen 1 7 nett Matematikk 1 modul 2

Grunnskolelærerutdanningen 1– 7, nett Matematikk 1, modul 2 Forelesning mandag 20. januar 2017 Algebra 3

Ulikheter • Jeg hadde gleden av å undervise i ulikheter da jeg var i praksis på ungdomsskolen høsten 2010. • Jeg oppdaget der en artig konsekvens av elevenes skjemaoppbygning når det gjaldt å finne svaret på en oppgave. • Svaret hadde nemlig alltid, helt siden elevene begynte på skolen, bestått av ett tall. Tilsvarende, når de tidligere hadde løst ligninger, var det også alltid ett tall x skulle være. • Så hvordan gikk det da elevene skulle løse oppgaver som x – 3 < 5 ? • Jo, elevene valgte ut et eksempel på hva x kunne være. F. eks. x = 4. Og satte to streker under.

Ulikheter • Ifølge forskning eksisterer følgende misforståelser blant elever, og også universitetsstudenter, innenfor ulikheter: • Elevene er usikre på hva ulikhetstegnene egentlig betyr. • Når de har løst en ulikhet, klarer de ikke å forstå hva løsningen betyr. • De tror at ulikhetene skal løses nøyaktig som ligninger. • Universitetsstudentene syntes låst fast til å kun holde seg til algebraiske løsningsmetoder, og det var alltid disse metodene som førte til flest feil i oppgavene. • Bakgrunnen for vanskelighetene synes å være manglende fordypning i bruk av ulikhetstegnene i barneskolen. R. V. Rowntree (2009): Students' Understandings and Misconceptions of Algebraic Inequalities. School Science and Mathematics, vol. 109, nr. 6, s. 311– 312. Mangler tillatelse til å legge ut på Fronter, men kan bestilles fra biblioteket. 1

Ulikheter • Visualisering av løsningene til ulikhetene (f. eks. grafiske løsninger) synes å redusere mange av misforståelsene. • Generelt er innføring av flere måter å løse ulikhetene på heldig for oppbygging av forståelsen.

De matematiske tegnene for ulikheter • En ulikhet er f. eks. 2 x > 3 eller 5+x < 6 x – 8. • Tegnene er: • • > > < < Betyr at uttrykket på venstre side er større enn høyre. Betyr at uttrykket på venstre side er større enn eller lik høyre. Betyr at uttrykket på venstre side er mindre enn eller lik høyre.

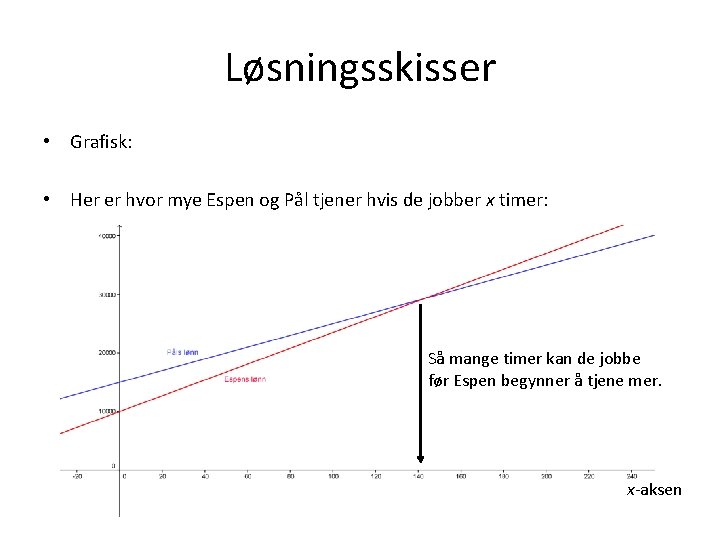
Oppgaveeksempel • Pål og Espen jobber sammen som dataprogrammerere. De jobber på timebasis, og jobber alltid like mye (siden de jobber sammen). Men de har ulike kontrakter. Pål har en fast månedslønn på 15 000 kr. og en timelønn på 100 kr på toppen av den faste lønnen. Espen har en fast månedslønn på 10 000 kr og en timelønn på 135 kr på toppen. • Pål blir veldig lett misunnelig hvis noen tjener mer enn ham. Så hvor mange timer i måneden kan Pål og Espen jobbe uten at Pål begynner å bli sur? • Svar: Vi setter opp en ulikhet. Påls lønn > Espens lønn. • Det blir 15 000 + 100 x > 10000 + 135 x

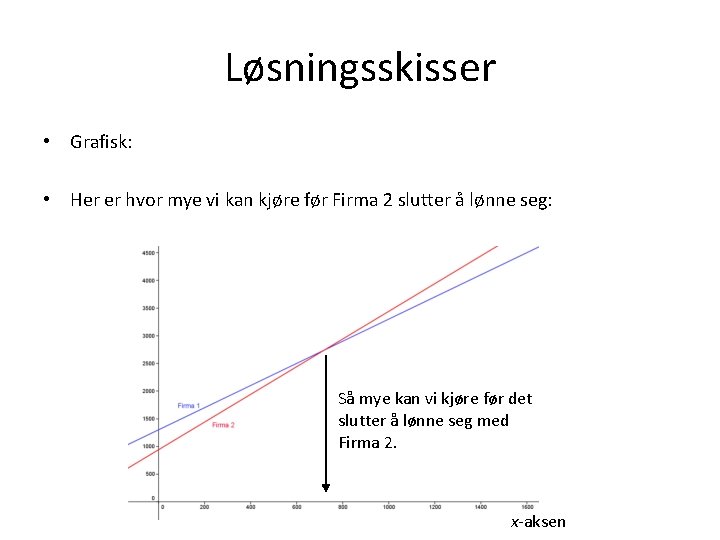
Oppgaveeksempel • Oppgaveeksempel fra alfa: To bilutleiefirmaer har følgende tilbud: • • Firma 1: 650 kr. pr. dag og 2 kr. pr. kilometer. Firma 2: 470 kr. pr. dag og 2, 5 kr. pr. kilometer. • Vi skal ha en leiebil i to dager, og så har vi gjort den tabben at vi har forpliktet oss til firma 2 uten å ha sjekket prisen hos firma 1 på forhånd. Hvor mye kan vi kjøre uten at vi har tapt på dealen? (Kan alternativt spørre hvor mye vi kan kjøre før vi har tapt på dealen. Det blir samme regnestykke. ) • Vi setter opp en ulikhet med x antall km. kjørt. Vi ønsker å ha Firma 2 < Firma 1 • 470· 2 + 2, 5 x < 650· 2 + 2 x

Løsningsskisser • Grafisk: • Her er hvor mye Espen og Pål tjener hvis de jobber x timer: Så mange timer kan de jobbe før Espen begynner å tjene mer. x-aksen

Løsningsskisser • Grafisk: • Her er hvor mye vi kan kjøre før Firma 2 slutter å lønne seg: Så mye kan vi kjøre før det slutter å lønne seg med Firma 2. x-aksen

Algebraisk løsning – legge til og trekke fra • Mange av de samme reglene som gjelder for ligninger, gjelder også for ulikheter. • x+2>4 • Hvilke x-er passer dette for? • Vi har x+2– 2>4– 2 • x>2 • Vi kan alltid trekke fra eller legge til det samme tallet på høyre og venstre side i en ulikhet.

Algebraisk løsning – ganging og deling •

Algebraisk løsning •

Ulikheter og negative tall • Vi har 3 < 5. • Men hvis vi ganger med – 1 på hver side, så er det ikke sånn at – 3 < – 5. Vi må snu ulikhetstegnet, slik at vi får – 3 > – 5. • Vi har 14 > 7. • Men hvis vi deler med – 7 på hver side, så er det ikke sånn at – 2 > – 1. Vi må igjen snu ulikhetstegnet, slik at vi får • – 2 < – 1.

Regler for deling og ganging • Vi har dermed følgende regler for ulikheter: • Vi kan alltid dele eller gange med et positivt tall på begge sider av ulikhetstegnet. • Hvis vi deler eller ganger med et negativt tall, må ulikhetstegnet snus.

Eksempler •

Eksempler •

Eksempler • NB! Merk!

Oppgaver •

Ligningssystemer med to ukjente •

Ligningssystemer med to ukjente •

Ligningssystemer med to ukjente • Men vanligvis kommer det til å være x-er og y-er i begge ligningene. Men løsningsmetoden vil faktisk fortsatt være den samme som vi nettopp viste. Metoden kalles for innsettingsmetoden. Vi viser nå eksempel 3. 79 på s. 261– 262 i alfa. x–y =1 x + 5 y = 13 • Vi begynner med å nummerere ligningene. Vi kaller den ene for I og den andre for II: I II x–y =1 x + 5 y = 13

Ligningssystemer med to ukjente • Så bruker vi ligning I til å få x alene på den ene siden: I I x–y =1 x=1+y • Vi har fortsatt den andre ligningen: II x + 5 y = 13 • Vi tar nå x-en i ligning II og bytter ut med 1+y , slik at vi får: II • 1+y + 5 y = 13 Nå er ligning II blitt gjort om til en ligning der vi bare har y som ukjent. Det er ingen x-er igjen i den ligningen.

Ligningssystemer med to ukjente • Vi løser ligning II: II II II 1+y + 5 y = 13 1 + 6 y = 13 – 1 6 y = 12/6 = 2. • Vi har altså at y = 2. Vi bruker nå ligning I til å finne x: I x–y=1 I x– 2=1 I x=1+2=3 • Endelig svar: (x, y) = (3, 2)

Ligningssystemer med to ukjente • Det finnes også en annen metode for å løse ligningssett, nemlig addisjonsmetoden: I II 3 x + y = 6 2 x – 2 y = 4 • Vi ganger ligning I med 2 på begge sider av likhetstegnet: I II 6 x + 2 y = 12 2 x – 2 y = 4

Ligningssystemer med to ukjente • Vi har altså I 6 x + 2 y = 12 II 2 x – 2 y = 4 • Nå plusser vi begge venstresidene sammen, og vi plusser begge høyresidene sammen. Vi kan gjøre det fordi hver enkelt høyreside er lik hver enkelt venstreside. Derfor vil summen av høyresidene også være lik summen av venstresidene: I+II 6 x + 2 y + 2 x – 2 y = 12 + 4 • Nå forsvinner y-ene, siden det sto +2 y i ligning I og – 2 y i ligning II. (Det var grunnen til at vi ganget ligning I med 2 i begynnelsen. ) Vi sitter altså igjen med kun x-er i ligningen.

Ligningssystemer med to ukjente • • Vi får: I+II Vi har altså at x=2. Vi må finne y. Da kan vi velge om vi vil bruke ligning I eller II. Ligning I er lettest å bruke i akkurat dette eksempelet: I I • 6 x + 2 y + 2 x – 2 y = 12 + 4 8 x = 16/8 = 2 3 x + y = 6 3· 2 + y = 6 6+y=6 y=6– 6=0 Endelig løsning: (x, y) = (2, 0)

Prøve • På samme måte som før går det fint an å sette prøve på ligningssystemene. • Ligning I: • V. s. : 3 x + y = 3· 2 + 0 = 6. • H. s. : 6. • Ligning II: • V. s. : 2 x – 2 y = 2· 2 – 2· 0 = 4 • H. s. : 4 • V. s. = h. s. på begge ligningene. OK.

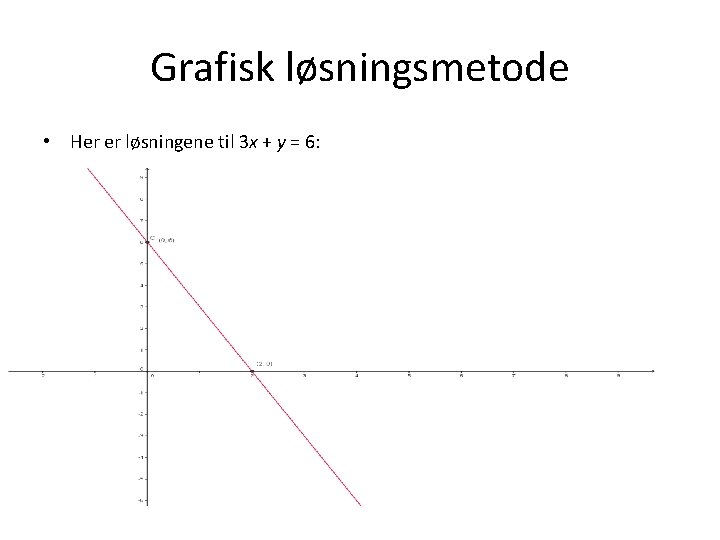
Grafisk løsningsmetode • La oss igjen se på det siste ligningssettet vi jobbet med: I 3 x + y = 6 II 2 x – 2 y = 4 • Hvis vi bare hadde ligning I, ville vi hatt følgende: 3 x + y = 6 • • Går det an å løse denne ligningen alene? Hvis vi setter inn f. eks. x = 0, så får vi 0 + y = 6. Altså er (x, y) = (0, 6) en løsning. • • Men setter vi inn x = 1, ser vi at y = 3. Altså er (x, y) = (1, 3) også en løsning. Og hvis x = 2, er y = 0. Altså er (x, y) = (2, 0) også en løsning. • Det viser seg at det finnes uendelig mange løsninger!

Grafisk løsningsmetode • Her er løsningene til 3 x + y = 6:

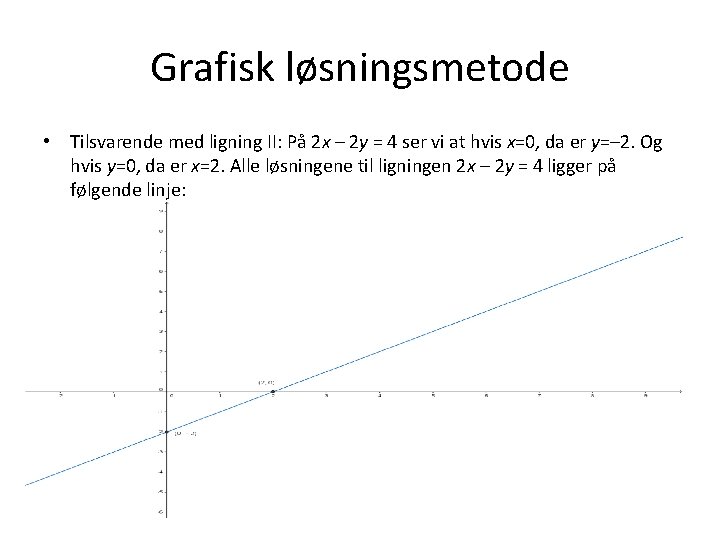
Grafisk løsningsmetode • Tilsvarende med ligning II: På 2 x – 2 y = 4 ser vi at hvis x=0, da er y=– 2. Og hvis y=0, da er x=2. Alle løsningene til ligningen 2 x – 2 y = 4 ligger på følgende linje:

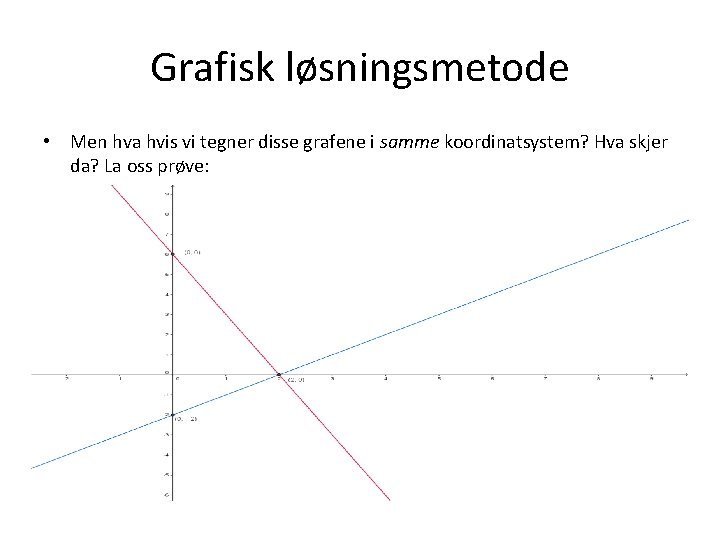
Grafisk løsningsmetode • Men hva hvis vi tegner disse grafene i samme koordinatsystem? Hva skjer da? La oss prøve:

Grafisk løsningsmetode • Grafene krysser hverandre i punktet (2, 0)! Altså punktet med x=2 og y=0. Og det var nøyaktig den løsningen vi fikk da vi løste ligningssettet! • Dette kalles for grafisk løsningsmetode. Vi lager en graf som viser alle løsningene for hver enkelt ligning. Og så ser vi hvor de to ligningene krysser hverandre.

Oppgaver • Løs ligningssystemene med bruk av innsettingsmetoden: 3 x + 9 y = 15 8 x – 6 y = 10 4 x + 20 y = – 8 3 x + 12 y = 3 • Sett opp et ligningssett og løs ved hjelp av addisjonsmetoden. 1 • Per Olsen hadde en bondegård, og på den gården hadde han både kalkuner og griser. Han tok med seg alle dyrene sine til dyrskuen i Seljord, og der fikk han solgt 10 griser og 40 kalkuner. De dyrene Olsen reiste hjem igjen til gården sin med hadde 100 bein og 30 hoder. • Hvor mange kalkuner hadde Per Olsen med seg fra Seljord? 1 Oppgaven er hentet fra http: //www. matematikk. org/uopplegg/vis. html? tid=83349&modus=elev.

Oppgaver dere kan regne hjemme • Alfa s. 281– 282: Oppgave 3. 60, 3. 61 (a), 3. 68, 3. 69, 3. 70.