Grunnskolelrerutdanningen 1 7 nett Matematikk 1 modul 2

Grunnskolelærerutdanningen 1– 7, nett Matematikk 1, modul 2 Forelesning mandag 13. februar 2017 Algebra 2

Ligninger • Det verserer mye forvirring i forbindelse med ligninger. • I en undersøkelse gjort blant australske 10. -klassinger 1, svarte 25 % av elevene feil på spørsmålet om hva ligningen a = 28 + b • betydde. (Her skulle elevene krysse av på riktig utsagn, og etterpå gi en begrunnelse for alternativet de valgte. ) • Blant de feilaktige svarene var følgende: – b var størst fordi den hadde 28 lagt til seg mens a ikke hadde noe lagt til seg. – a var lik 28. Og så legger vi til b. – Det er ikke mulig å bestemme hva a og b kan være, siden de kan være hva som helst. 1 Se K. Stacey og M. Mac. Gregor (1997): Ideas about symbolism that students bring to algebra. The 90(2): 110– 113. Mathematics Teacher,

Ligninger • Ligninger skal forstås på følgende måte: Uttrykket på høyre side av likhetstegnet skal alltid være lik uttrykket på venstre side. dette kalles for den ukjente disse kalles for konstanter • I ligningen 7 x + 3 = 5 x + 9 • har vi dermed at x er ukjent, men at vi vet at 5 x + 3 er like stort som 7 x + 9. • Vi løser ligningen ved å alltid trekke fra og legge til det samme tallet på hver side. Vi kan dermed begynne med å trekke fra 3 på begge sider slik at vi ikke har noen konstanter igjen på venstre side. Vi har da: 7 x + 3 – 3 = 5 x + 9 – 3 7 x = 5 x + 6

Ligninger disse kalles for koeffisienter •

Ligninger •

Ligninger • Vi må alltid sette prøve på ligningen etterpå. Det betyr at vi må bytte ut alle x-ene med 3 -tall i den opprinnelige ligningen for å sjekke at det faktisk er riktig svar. Det gjør vi slik: • Venstre side: 7 x + 3 = 7· 3 + 3 = 24. • Høyre side: 5 x + 9 = 5· 3 + 9 = 24. • Venstre side = høyre side. OK.

Ligninger • For de som blir litt forvirret av alle likhetstegnene, kan prøven også settes på følgende måte: • Venstre side: 7 x + 3 7· 3 + 3 24 • Høyre side: 5 x + 9 5· 3 + 9 24 • Venstre side = høyre side. OK.

Prealgebra • I barneskolen får elevene ofte arbeide med prealgebra, som er matematikkstykker som klargjør dem for arbeidet med ligninger de kommer til å møte på ungdomsskolen. Dette er stykker som 50 = 20 + · 2 eller 51 + 9 = 8 · + 4. • Slike oppgaver har to formål: • 1. Å ha noe konkret å knytte x-en opp mot når den introduseres. • 2. Å gjøre elevene vant til likhetstegnets betydning. Forskning har nemlig avdekket at mange elever oppfatter likhetstegnet som en beskjed om at «noe skal utføres» heller enn at det som står på høyre og venstre side er like stort. 2 2 Se L. S. Grønmo og B. Rosén (1998): Att förstå algebra. Nämnaren, 1: 46– 49.

Husk! •

Husk! •

Oppgaver • Løs ligningene: 5 x – 4 = 3 x + 6 2 z + 3 z – 8 = 9 z + 12 3, 2 a + 5, 47 = – 11, 23 + 7, 345 a + 2, 89 a

Enkle andregradsligninger •

Enkle andregradsligninger • Dette symbolet betyr «eller» . Dette kalles for løsningsmengden, og er det endelige svaret på oppgaven. Dette betyr at x kan være – 2 eller 10. Vi kan også bruke løsningsmengde på ligninger med bare én løsning.

Enkle andregradsligninger • Prøve for x = – 2: Venstre side: (x – 4)2 = (– 2 – 4)2 = (– 6)2 = 36 Høyre side: 36 Venstre side = høyre side = 36. OK. • Prøve for x = 10: Venstre side: (x – 4)2 = (10 – 4)2 = 62 = 36 Høyre side: 36 Venstre side = høyre side = 36. OK.

Enkle andregradsligninger • Men hva med følgende type ligninger? x 2 – 3 x = 0 • Her kan vi ikke ta kvadratrot. Og selv om vi har x-ene samlet på én side, kan vi ikke trekke dem sammen eller dele på noen koeffisient slik at vi ender opp med bare én x alene på venstre side. • Hva skal vi gjøre?

Enkle andregradsligninger •

Enkle andregradsligninger •

Formelt oppsett •

Formelt oppsett • Prøve for x=0: Venstre side: x 2 – 3 x = 02 – 3· 0 = 0 Høyre side: 0 Venstre side = høyre side = 0. OK. • Prøve for x=3: Venstre side: x 2 – 3 x = 32 – 3· 3 = 0 Høyre side: 0 Venstre side = høyre side = 0. OK.

Ikke dele med null •

Ikke dele med null •

Nytt eksempel på enkel andregradsligning •

Nytt eksempel på enkel andregradsligning •

Oppgaver • Løs følgende enkle andregradsligninger: x 2 = 49 (x – 2)2 = 9 (x + 4)2 = 16 x 2 – 5 x = 0 x 2 = 3 x • (Litt utfordrende) Løs følgende ligninger: (Hint: Tenk kvadratsetningene. ) x 2 + 2 x + 1 = 0 x 2 – 2 x + 1 = 36

Generelle andregradsligninger • Veldig viktig å huske

Generelle andregradsligninger •

Generelle andregradsligninger • Prøve for x ≈ – 2, 84: Venstre side: 3 x 2 + 5 x – 10 = 3· (– 2, 84)2 + 5·(– 2, 84) – 10 ≈ 0 Høyre side: 0 Venstre side = høyre side = 0. OK. • Prøve for x ≈ 1, 17: Venstre side: 3 x 2 + 5 x – 10 = 3· 1, 172 + 5· 1, 17 – 10 ≈ 0 Høyre side: 0 Venstre side = høyre side = 0. OK.

Generelle andregradsligninger •

Oppgaver • Løs følgende ligninger: 2 x 2 + 10 x + 3 = 0 5 x 2 + 4 = 9 x – 4 x 2 + 3 x = 2 x 2 – 4 x + 1

Oppgaver dere kan jobbe med hjemme • Alfa s. 279– 282: 3. 40, 3. 41, 3. 42, 3. 44 (d) (e), 3. 52 (a), 3. 54 (bruk bare andregradsformelen), 3. 58, 3. 71.

Problemløsningsoppgaver • Noen problemløsningsoppgaver dere kan tenke på (hentet fra Developing Thinking in Algebra av Mason, Graham og Johnston-Wilder): • Velg hvilke som helst tre etterfølgende heltall (f. eks. 3, 4, 5 eller 20, 21, 22). Summen av disse tre tallene vil alltid være delelig med 3. Hvorfor? • Velg nå et tall som er delelig med 3. Kan vi alltid finne tre etterfølgende heltall der summen blir dette tallet? (Hvis vi f. eks. velger 9, finner vi at dette er summen av 2, 3 og 4. ) Ikke pensum. Kun for de som er interesserte. Ta kontakt med meg direkte hvis dere vil ha løsningen.

Problemløsningsoppgaver • Problemløsningsoppgave fra Breiteig: Bevisets didaktiske karakter. Normat, 1987: • Skriv ned et tall opp til 15. Skriv ned det neste tallet. Adder de to tallene og skriv ned svaret. Du har nå skrevet tre tall. Gerd sier at nøyaktig ett av disse finnes i listen 3, 6, 9, 12, 15, 18, 21, 24, 27, 30. • 1. Har hun rett? • 2. Har hun alltid rett, også for større tall? • 3. Forklar hvorfor. Ikke pensum. Kun for de som er interesserte. Ta kontakt med meg direkte hvis dere vil ha løsningen.

Problemløsningsoppgaver • 1. Problemløsningsoppgave fra Breiteig: Bevisets didaktiske karakter. Normat, 1987: (Kanskje ikke akkurat problemløsning, men kan være en fin utfordring. ) Start med 6, doble det, 12, og adder til det neste tallet, 13. 12+13=25. Starter på 6, slutter på 25. • Start med 11, doble det, 22, og adder 22+23. Svaret er 45. Du starter på 11 og ender på 45. • Gjør to flere regnestykker. • Kan du slutte på tallet 13? Hva må du i så fall starte på? Kan du slutte på 21? På 14? 2. 3. 4. Finn regler for hvilke tall du kan få og hvilke du ikke kan få som slutt-tall. Finn også en regel for å finne starttallet når sluttallet er oppgitt. For hver av reglene, si om den alltid er sann – eller bare av og til – og si hvorfor. Ikke pensum. Kun for de som er interesserte. Ta kontakt med meg direkte hvis dere vil ha løsningen.

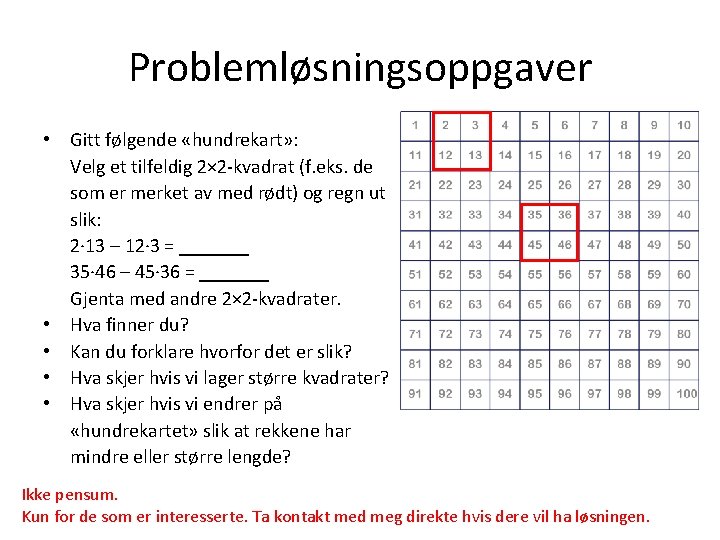
Problemløsningsoppgaver • • • • Gitt følgende «hundrekart» : Velg et tilfeldig 2× 2 -kvadrat (f. eks. de som er merket av med rødt) og regn ut slik: 2· 13 – 12· 3 = _______ 35· 46 – 45· 36 = _______ Gjenta med andre 2× 2 -kvadrater. Hva finner du? Kan du forklare hvorfor det er slik? Hva skjer hvis vi lager større kvadrater? Hva skjer hvis vi endrer på «hundrekartet» slik at rekkene har mindre eller større lengde? Ikke pensum. Kun for de som er interesserte. Ta kontakt med meg direkte hvis dere vil ha løsningen.