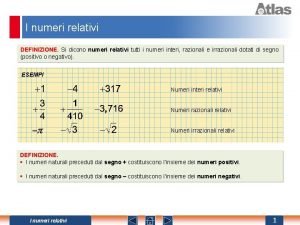
GLI INSIEMI RAPPRESENTAZIONE Per rappresentare un qualsiasi insieme













- Slides: 40

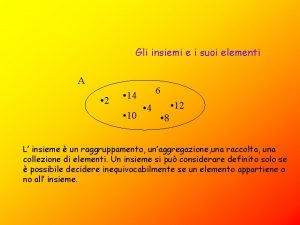
GLI INSIEMI

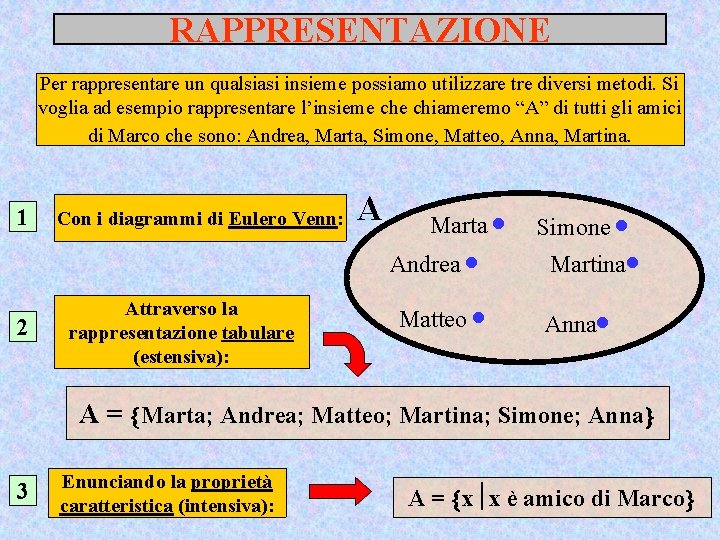
RAPPRESENTAZIONE Per rappresentare un qualsiasi insieme possiamo utilizzare tre diversi metodi. Si voglia ad esempio rappresentare l’insieme chiameremo “A” di tutti gli amici di Marco che sono: Andrea, Marta, Simone, Matteo, Anna, Martina. 1 Con i diagrammi di Eulero Venn: A Marta Andrea 2 Attraverso la rappresentazione tabulare (estensiva): Matteo Simone Martina Anna A = Marta; Andrea; Matteo; Martina; Simone; Anna 3 Enunciando la proprietà caratteristica (intensiva): A = x x è amico di Marco

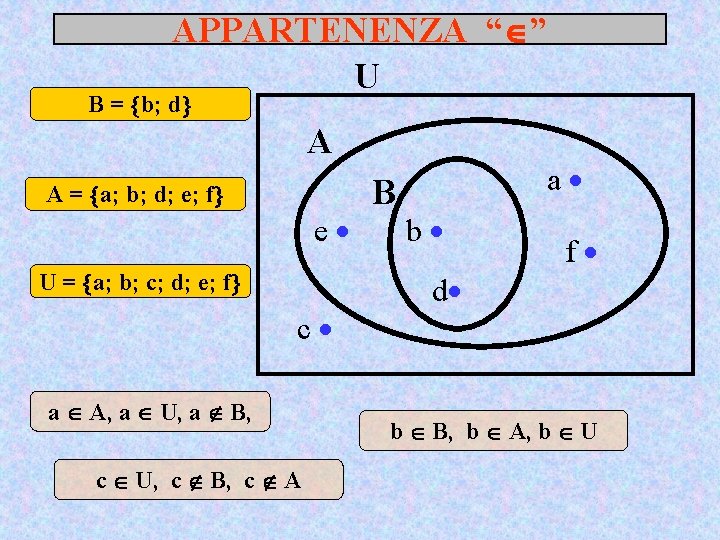
APPARTENENZA “ ” U B = b; d A A = a; b; d; e; f e U = a; b; c; d; e; f c a A, a U, a B, c U, c B, c A B a b f d b B, b A, b U

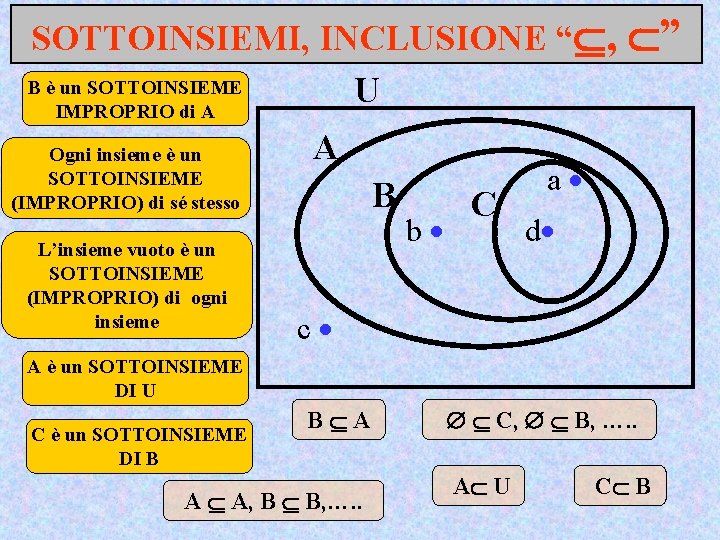
SOTTOINSIEMI, INCLUSIONE “ , B è un SOTTOINSIEME U IMPROPRIO di A Ogni insieme è un SOTTOINSIEME (IMPROPRIO) di sé stesso L’insieme vuoto è un SOTTOINSIEME (IMPROPRIO) di ogni insieme A B b C ” a d c A è un SOTTOINSIEME DI U C è un SOTTOINSIEME DI B B A A A, B B, …. . C, B, …. . A U C B

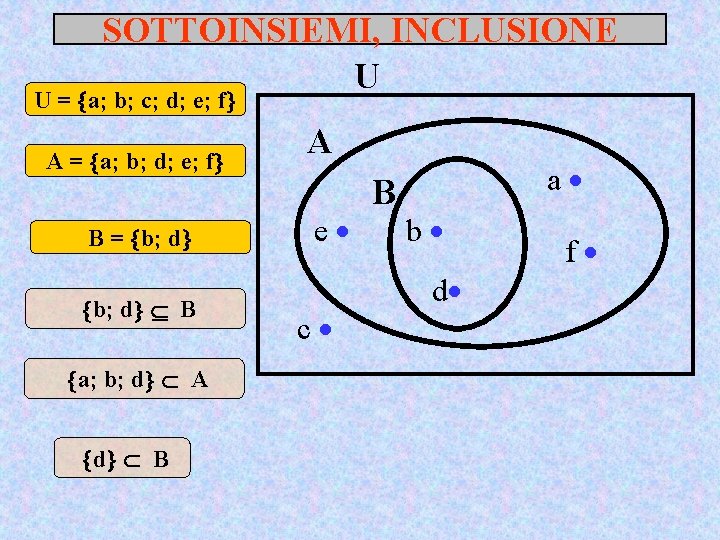
SOTTOINSIEMI, INCLUSIONE U U = a; b; c; d; e; f A = a; b; d; e; f B = b; d B a; b; d A d B A e c B a b d f

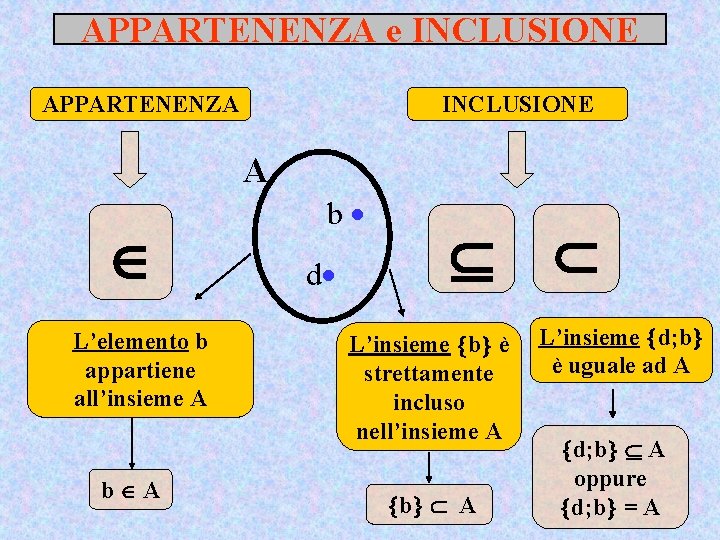
APPARTENENZA e INCLUSIONE APPARTENENZA INCLUSIONE A L’elemento b appartiene all’insieme A b d L’insieme b è strettamente incluso nell’insieme A b A L’insieme d; b è uguale ad A d; b A oppure d; b = A

Esercizio 1 Dati gli insiemi A={a, b, c} e B= {a, b, e, c, d} A B? SI NO

Esercizio 2 Dati gli insiemi A={a, b, c, r} e B= {a, b, e, c, t} A B? SI NO

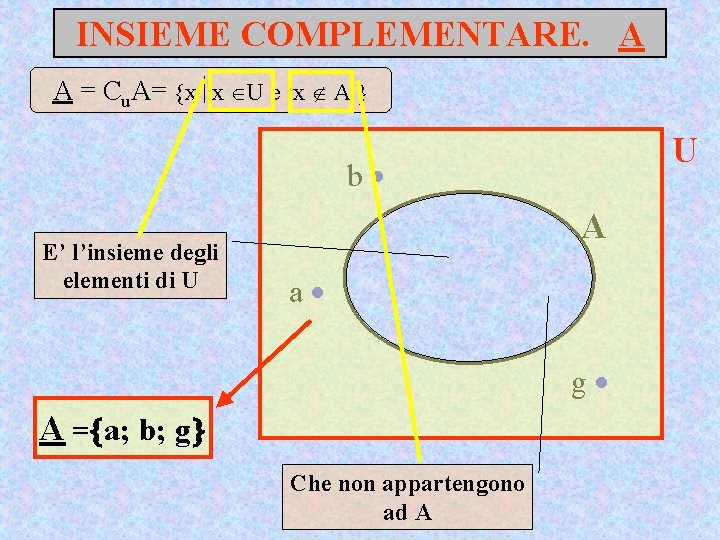
INSIEME COMPLEMENTARE. A A = Cu. A= x x U e x A U b E’ l’insieme degli elementi di U a c d f e A g A = a; b; g Che non appartengono ad A

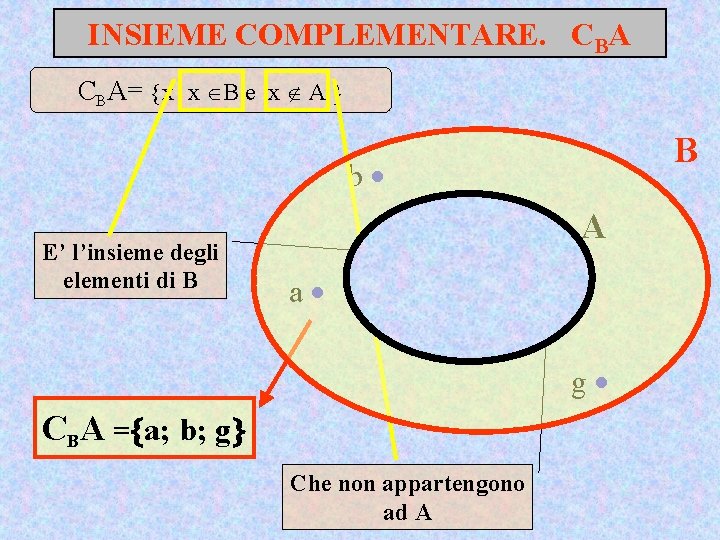
INSIEME COMPLEMENTARE. CBA= x x B e x A B b E’ l’insieme degli elementi di B a c d f e A g CBA = a; b; g Che non appartengono ad A

Esercizio Dati gli insiemi A={a, b} e B ={a, c, b, e} Trova il complementare di A rispetto a B 1) {c, e} 2) {a, e} 3) {a, b} 4) {c, b}

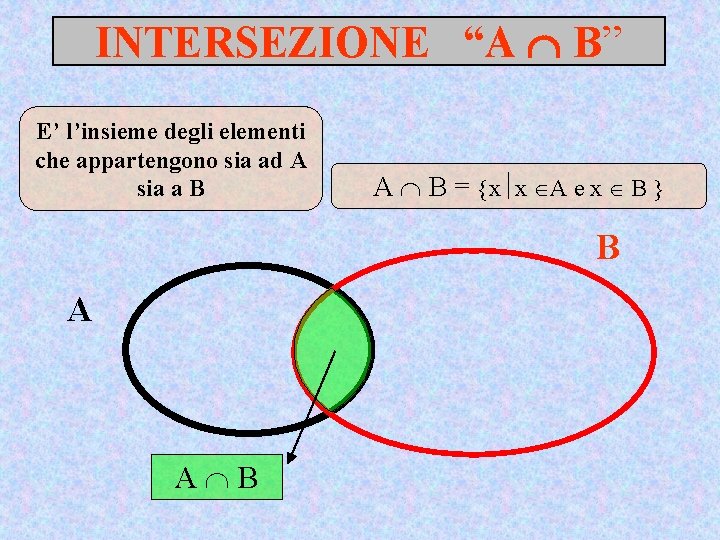
INTERSEZIONE “A B” E’ l’insieme degli elementi che appartengono sia ad A sia a B A B = x x A e x B B A A B

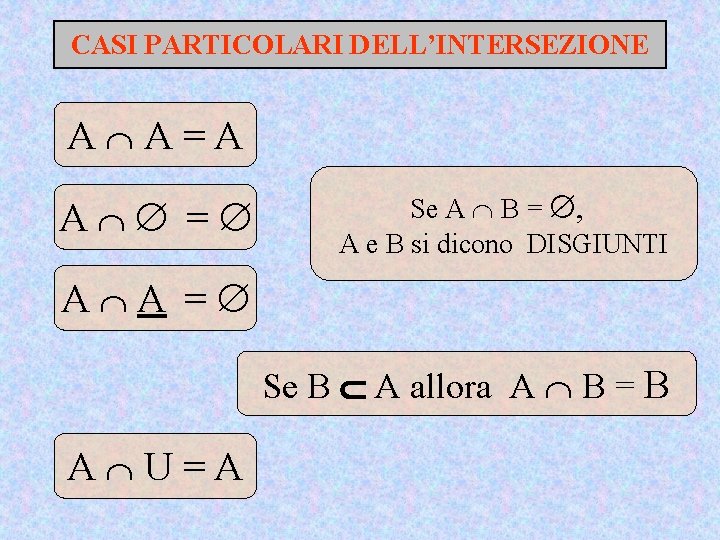
CASI PARTICOLARI DELL’INTERSEZIONE A A=A A = Se A B = , A e B si dicono DISGIUNTI A A = Se B A allora A B = B A U=A

Esercizio Dati gli insiemi A={a, b, d} e B ={a, c, b, e} Trova A B 1){a, b, c} 2){a, b, d, c, } 3) {a, b} 4) {c, b}

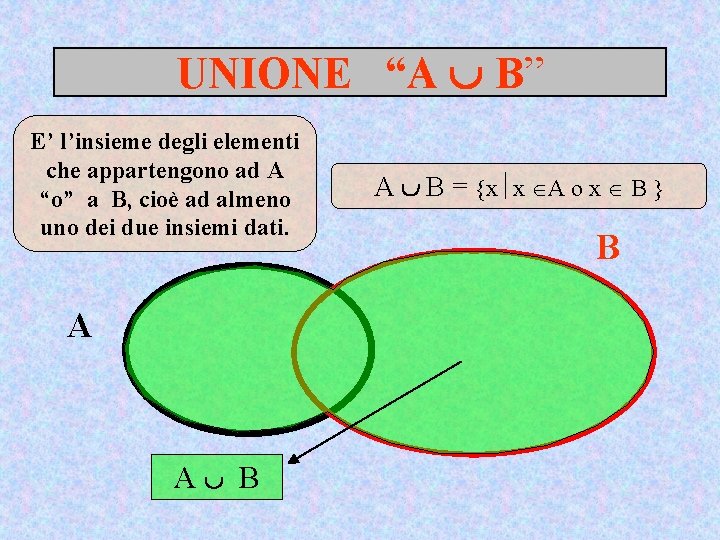
UNIONE “A B” E’ l’insieme degli elementi che appartengono ad A “o” a B, cioè ad almeno uno dei due insiemi dati. A A B A B = x x A o x B B

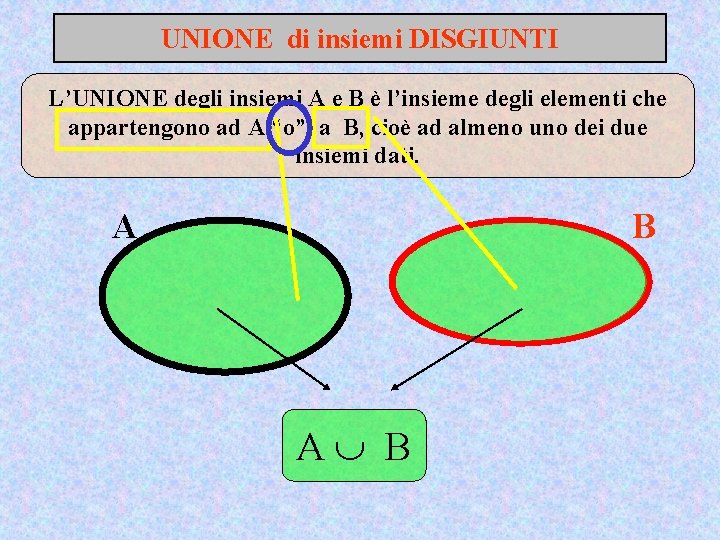
UNIONE di insiemi DISGIUNTI L’UNIONE degli insiemi A e B è l’insieme degli elementi che appartengono ad A “o” a B, cioè ad almeno uno dei due insiemi dati. A B

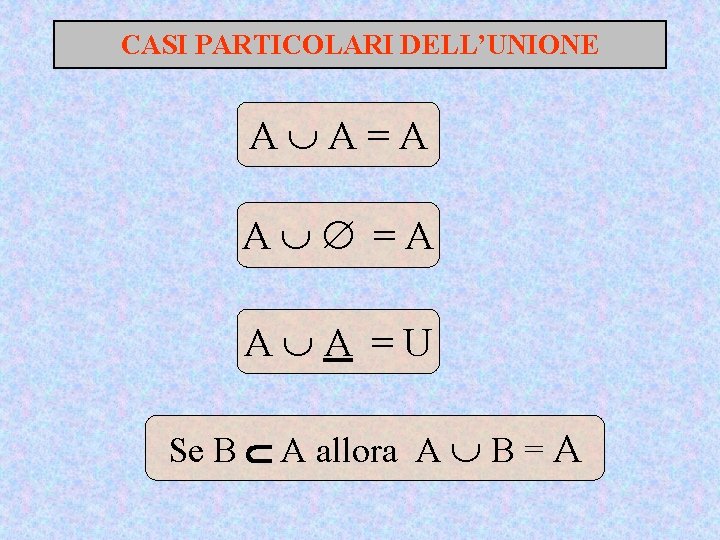
CASI PARTICOLARI DELL’UNIONE A A=A A A =U Se B A allora A B = A

Esercizio Dati gli insiemi A={a, d} e B ={a, c, b, } Trova A B 1){a, b, c} 2){a, d, c, b} 3) {a} 4){a, d, a, c, b}

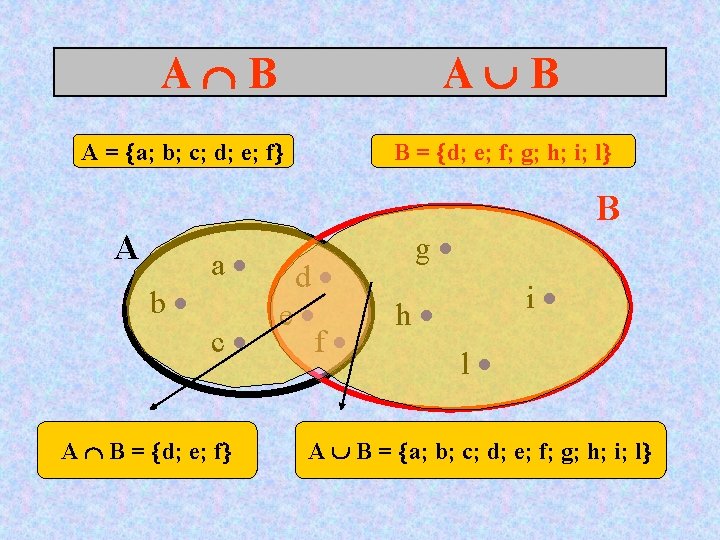
A B A = a; b; c; d; e; f A a B = d; e; f; g; h; i; l d b e c f A B = d; e; f B g i h l A B = a; b; c; d; e; f; g; h; i; l

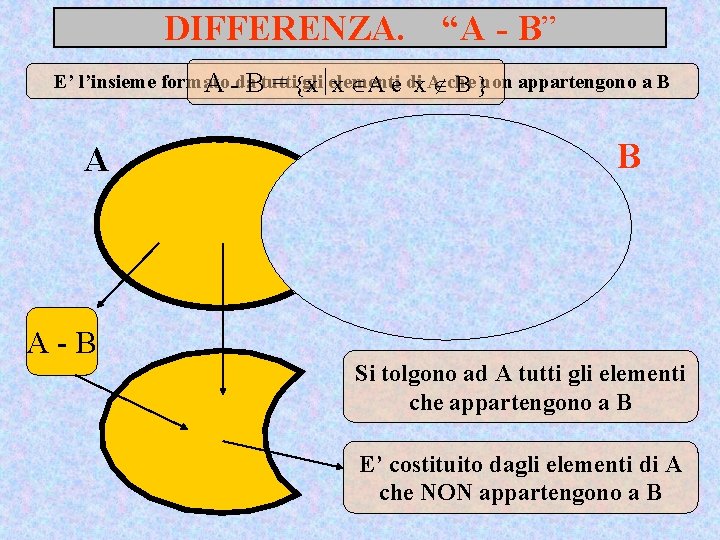
DIFFERENZA. “A - B” E’ l’insieme formato gli elementi A -da. Btutti = x x A e dix A che B non appartengono a B A A-B B Si tolgono ad A tutti gli elementi che appartengono a B E’ costituito dagli elementi di A che NON appartengono a B

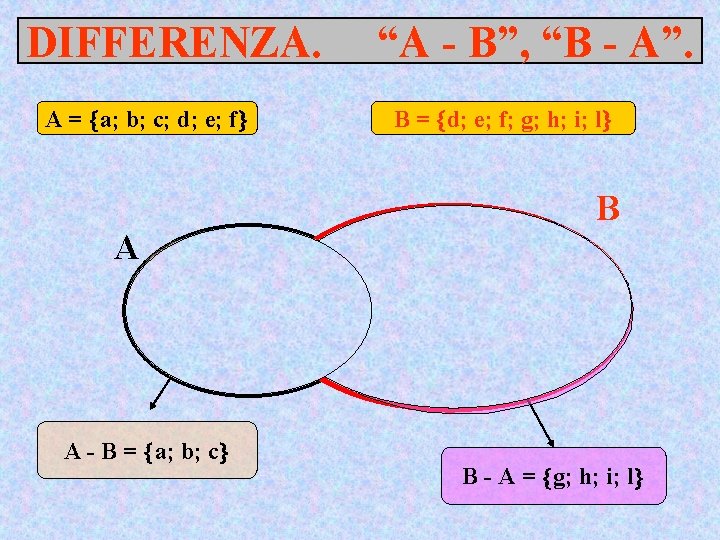
DIFFERENZA. A = a; b; c; d; e; f A a d b e c f A - B = a; b; c “A - B”, “B - A”. B = d; e; f; g; h; i; l B g i h l B - A = g; h; i; l

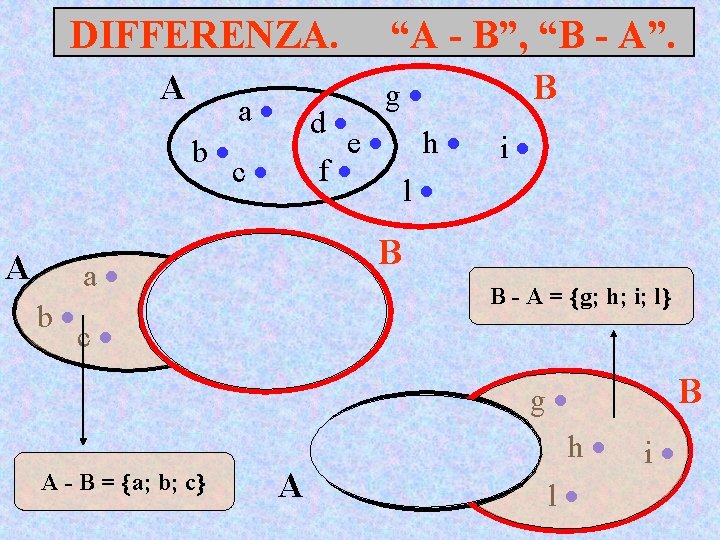
DIFFERENZA. A A a b c g d e h f l a b “A - B”, “B - A”. c g d e h f l A i B B - A = g; h; i; l i a A - B = a; b; c B b c g d e h f l B i

CASI PARTICOLARI DELLA DIFFERENZA TRA INSIEMI A-A= A- =A Se A B = allora A - B = A e B - A = B Se B A allora B - A =

Esercizio Dati gli insiemi A={a, b, c, d} e B ={a, c, b, e} Trova A - B 1){d} 2){e} 3) {d, e} 2){a, d, a, c, b}

INSIEME DELLE PARTI “P(A)” Dato un insieme A, l’insieme di tutti i suoi SOTTOINSIEMI propri e impropri, si definisce insieme delle parti di A e si indica A = a; b; c; A b a a con P(A) c b I possibili SOTTOINSIEMI di A L’insieme delle parti di A è: sono: c a; b a; c b; c a; b; c P(A) = ; a ; b ; c ; a; b ; a; c ; b; c ; a; b; c Gli elementi di P(A) sono INSIEMI Se A contiene n elementi, P(A) ne contiene 2 n

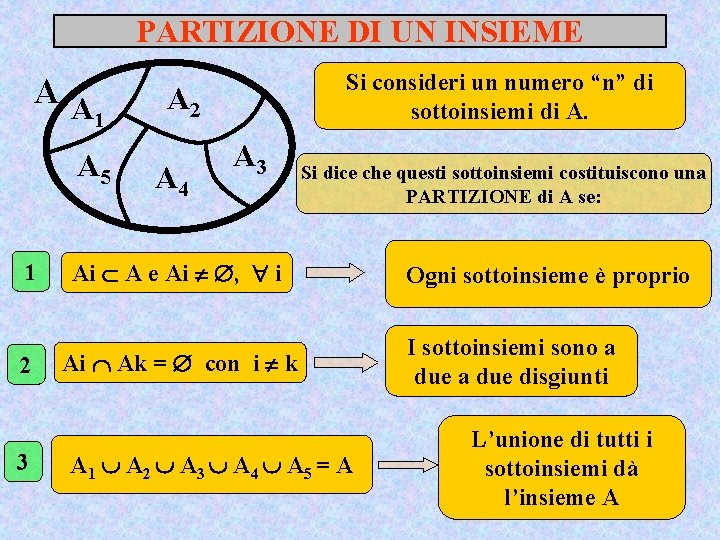
PARTIZIONE DI UN INSIEME AA 1 A 5 1 2 3 Si consideri un numero “n” di sottoinsiemi di A. A 2 A 4 A 3 Si dice che questi sottoinsiemi costituiscono una PARTIZIONE di A se: Ai A e Ai , i Ai Ak = con i k A 1 A 2 A 3 A 4 A 5 = A Ogni sottoinsieme è proprio I sottoinsiemi sono a due disgiunti L’unione di tutti i sottoinsiemi dà l’insieme A

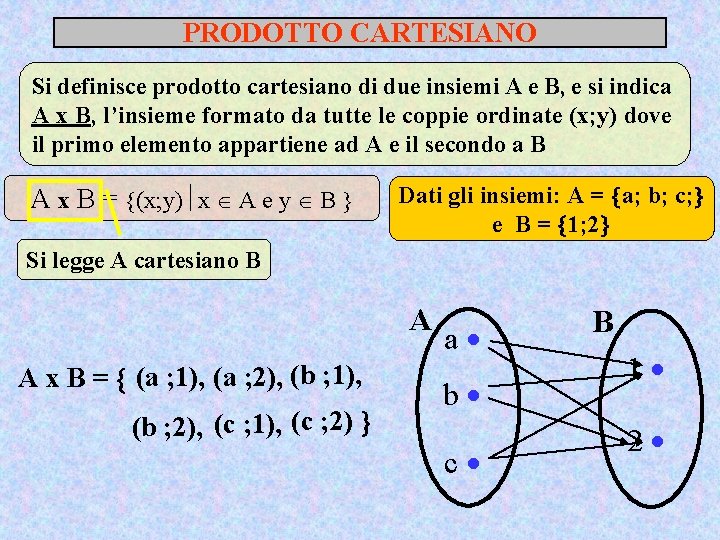
PRODOTTO CARTESIANO Si definisce prodotto cartesiano di due insiemi A e B, e si indica A x B, l’insieme formato da tutte le coppie ordinate (x; y) dove il primo elemento appartiene ad A e il secondo a B A x B = (x; y) x A e y B Dati gli insiemi: A = a; b; c; e B = 1; 2 Si legge A cartesiano B A A x B = (a ; 1), (a ; 2), (b ; 1), (b ; 2), (c ; 1), (c ; 2) a b c B 1 2

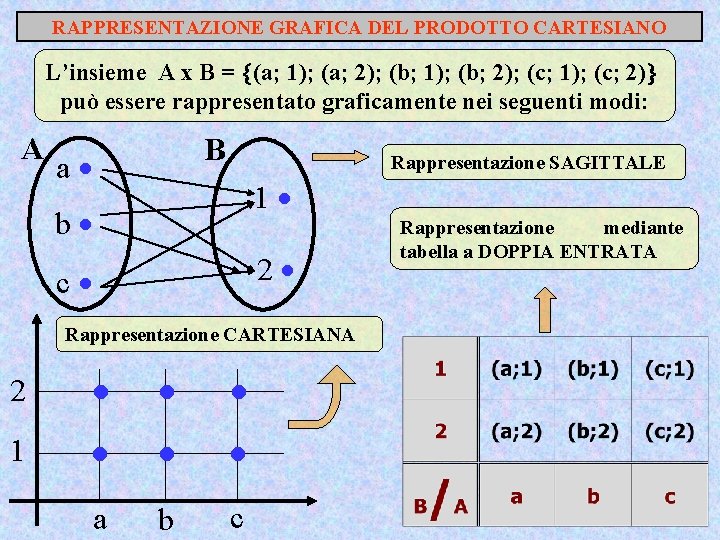
RAPPRESENTAZIONE GRAFICA DEL PRODOTTO CARTESIANO L’insieme A x B = (a; 1); (a; 2); (b; 1); (b; 2); (c; 1); (c; 2) può essere rappresentato graficamente nei seguenti modi: A B a Rappresentazione SAGITTALE 1 b 2 c Rappresentazione CARTESIANA 2 1 a b c Rappresentazione mediante tabella a DOPPIA ENTRATA

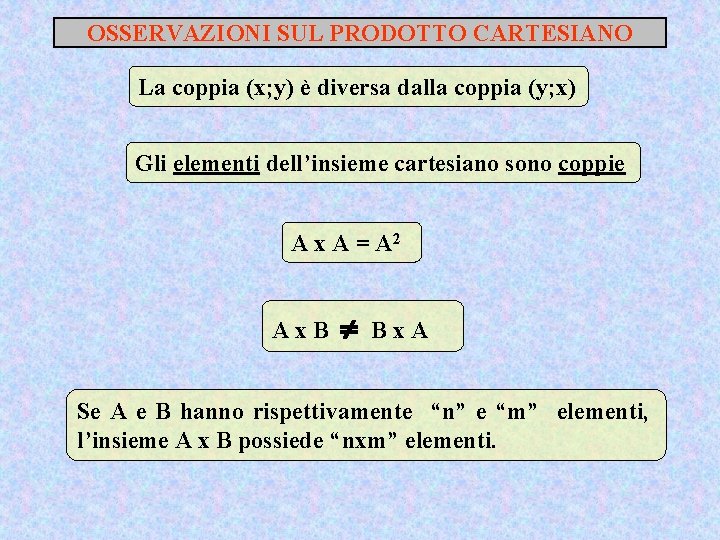
OSSERVAZIONI SUL PRODOTTO CARTESIANO La coppia (x; y) è diversa dalla coppia (y; x) Gli elementi dell’insieme cartesiano sono coppie A x A = A 2 Ax. B Bx. A Se A e B hanno rispettivamente “n” e “m” elementi, l’insieme A x B possiede “nxm” elementi.

LE STRANEZZE DEGLI INSIEMI INFINITI

Rispondi: N = 0; 1; P = 0; 2; 4; L’insieme dei numeri pari P è un sottoinsieme proprio dell’insieme dei numeri naturali N? 3; 6; 4; 8; 5; 6; 7; 10…. 8; 9; 10; 11; 12; . . Si! Infatti per costruire P scelgo solo alcuni elementi di N. Quale insieme ha più elementi? N o P? Se P ha meno elementi, come si è portati a pensare essendo P un sottoinsieme proprio di N, contando gli elementi di P ad un certo punto ci si dovrà fermare, proprio come succede quando si conta il numero delle stanze della casa dove abitiamo! PROVA A CONTARE UTILIZZANDO LE DITA IL NUMERO DELLE STANZE DELLA TUA CASA!!!!

Proviamo a contare quanti elementi (numeri) ha P. Invece che contare utilizzando le dita come facciamo qualche volta, utilizziamo l’insieme N e delle frecce. Per ora trascuriamo lo zero. N = 1; 2; P = 2; 3; 4; 6; 5; 8; 6; 10; 7; 12; 8; 9; 10; 11; 12; . . 14; 16; 18…. A quale numero ci fermiamo? ? ? Quanti sono gli elementi di P? ? Chi ha più elementi N o P? Abbiamo ottenuto un risultato assai strano! Dato un insieme con un numero infinito di elementi è possibile che un suo SOTTOINSIEME PROPRIO abbia lo stesso numero di elementi!!!

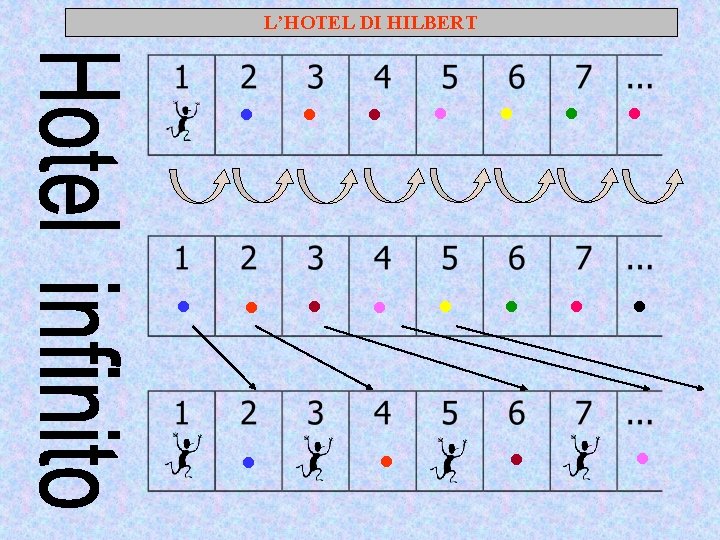
L’HOTEL DI HILBERT

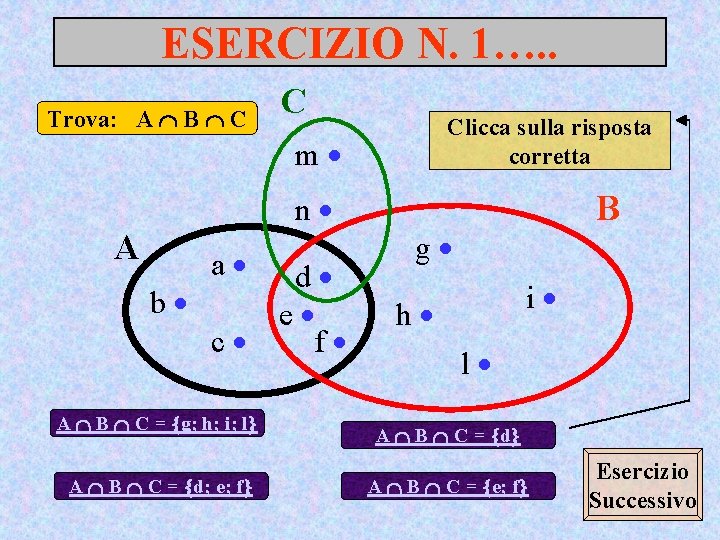
ESERCIZIO N. 1…. . Trova: A B C C Clicca sulla risposta corretta m n A a d b e c f A B C = g; h; i; l A B C = d; e; f B g i h l A B C = d A B C = e; f Esercizio Successivo

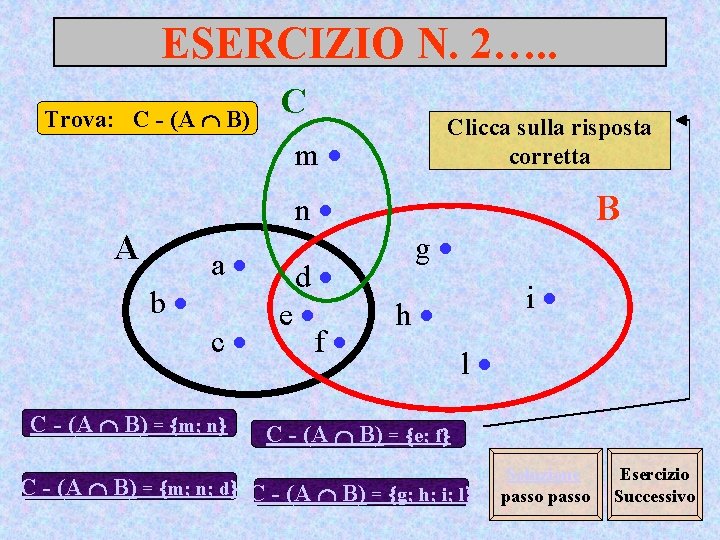
ESERCIZIO N. 2…. . Trova: C - (A B) C Clicca sulla risposta corretta m n A a d b e c f C - (A B) = m; n B g i h l C - (A B) = e; f C - (A B) = m; n; d C - (A B) = g; h; i; l Soluzione passo Esercizio Successivo

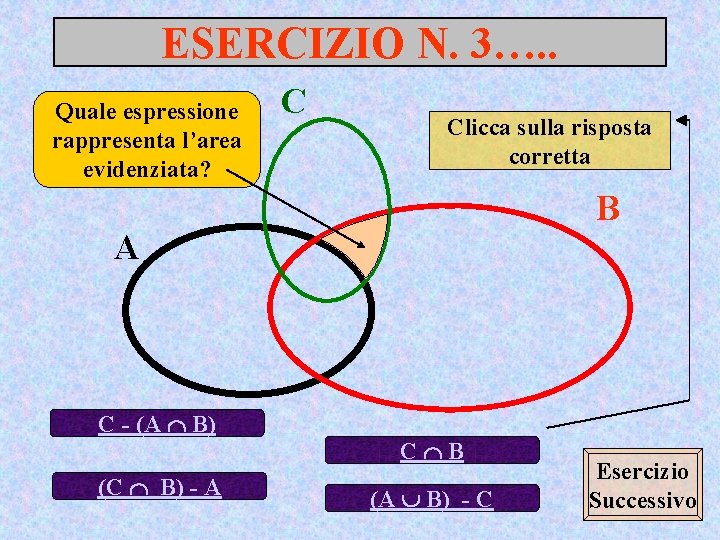
ESERCIZIO N. 3…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A C - (A B) (C B) - A C B (A B) - C Esercizio Successivo

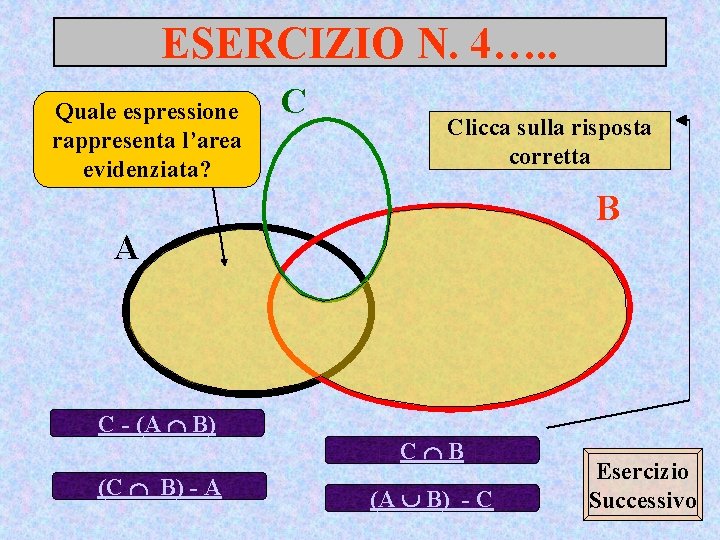
ESERCIZIO N. 4…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A C - (A B) (C B) - A C B (A B) - C Esercizio Successivo

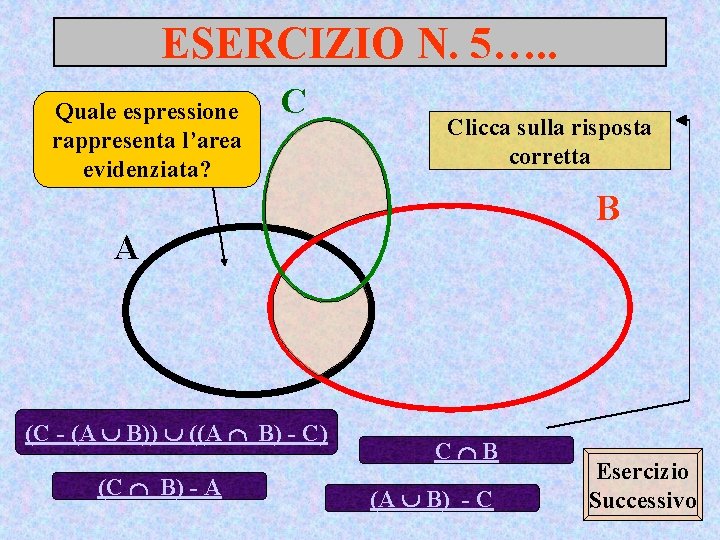
ESERCIZIO N. 5…. . Quale espressione rappresenta l’area evidenziata? C Clicca sulla risposta corretta B A (C - (A B)) ((A B) - C) (C B) - A C B (A B) - C Esercizio Successivo

TEORIA DEGLI INSIEMI COMPLIMENTI RISPOSTA ESATTA!!!! Ritorna alla diapositiva precedente

TEORIA DEGLI INSIEMI MI DISPIACE RISPOSTA ERRATA!!!! Ritorna alla diapositiva precedente
 Rappresentazione intensiva di un insieme
Rappresentazione intensiva di un insieme Scala di riduzione carta geografica
Scala di riduzione carta geografica Non ti auguro un dono qualsiasi
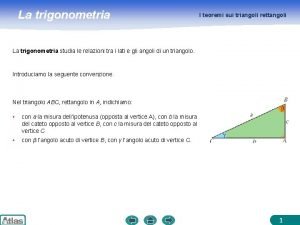
Non ti auguro un dono qualsiasi Trigonometria triangoli
Trigonometria triangoli Le regole da rispettare a scuola
Le regole da rispettare a scuola Insieme per viaggiare
Insieme per viaggiare Insieme per un mondo migliore
Insieme per un mondo migliore Fisica
Fisica Prodotto cartesiano a x b x c
Prodotto cartesiano a x b x c Simboli insiemi
Simboli insiemi Bertrand russell paradosso
Bertrand russell paradosso Insiemi disgiunti
Insiemi disgiunti Linguaggio insiemi
Linguaggio insiemi Insiemi disgiunti
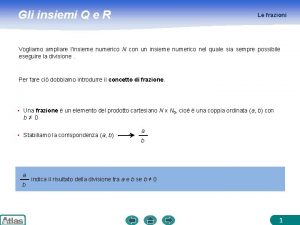
Insiemi disgiunti Numeri irrazionali
Numeri irrazionali Unione tra due insiemi
Unione tra due insiemi Voi che per li occhi mi passaste 'l core
Voi che per li occhi mi passaste 'l core Come calcolare gli oneri per la sicurezza?
Come calcolare gli oneri per la sicurezza? Biscia divisione in sillabe
Biscia divisione in sillabe Curare se stessi per curare gli altri
Curare se stessi per curare gli altri L'orchestra è un insieme di
L'orchestra è un insieme di Bruner attivo iconico simbolico
Bruner attivo iconico simbolico Potenza numeri relativi
Potenza numeri relativi Invariante di rappresentazione
Invariante di rappresentazione Strofa di 7 versi
Strofa di 7 versi Insieme di procedure
Insieme di procedure La carta geografica è una rappresentazione bidimensionale
La carta geografica è una rappresentazione bidimensionale Uova e pesce insieme
Uova e pesce insieme Retta dei numeri
Retta dei numeri Insieme di cromosomi
Insieme di cromosomi Rappresentazione numeri reali
Rappresentazione numeri reali Rappresentazione grafica delle disequazioni
Rappresentazione grafica delle disequazioni Impariamo insieme matematica
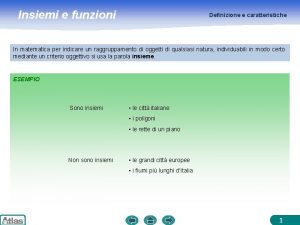
Impariamo insieme matematica Definizione di insieme matematico
Definizione di insieme matematico Enti geometrici primitivi
Enti geometrici primitivi Quotatura foro filettato
Quotatura foro filettato Ombra propria e portata
Ombra propria e portata Pseudocodifica esempi
Pseudocodifica esempi Proposizioni mentali
Proposizioni mentali Rappresentazione simbolica bruner
Rappresentazione simbolica bruner Tecniche di rappresentazione dello spazio
Tecniche di rappresentazione dello spazio