General Structural Equation LISREL Models Week 3 1

General Structural Equation (LISREL) Models Week 3 #1 l. Multiple Group Models l. An extended multiple-group model: Religiosity & Sexual Morality in 2 countries (LISREL example) l Computer programming for multiple-group models: a) LISREL b) AMOS –See Week 3 Examples 1

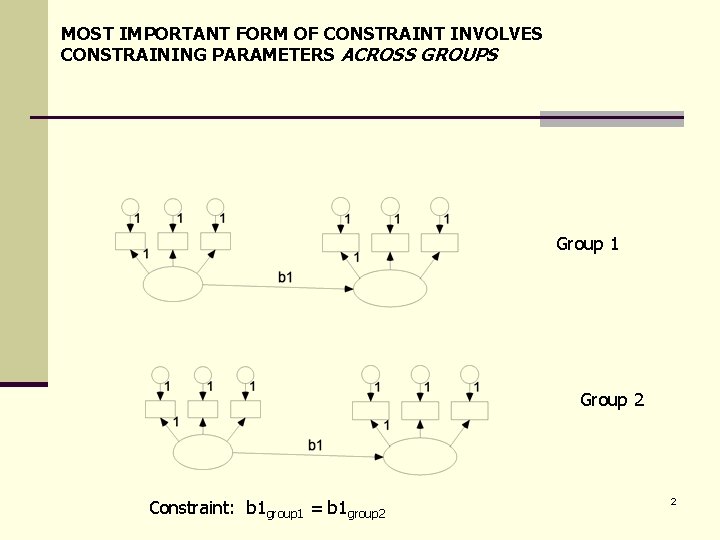
MOST IMPORTANT FORM OF CONSTRAINT INVOLVES CONSTRAINING PARAMETERS ACROSS GROUPS Group 1 Group 2 Constraint: b 1 group 1 = b 1 group 2 2

Multiple Group Models Group 2 (female) Group 1 (male) Equivalence of measurement coefficients H 0: Λ[1] = Λ[2] lambda 1 [1] = lambda 1 [2] df=2 lambda 2 [1] = lambda 2 [2] From last Friday 3

Multiple Group Models Other equivalence tests possible: 1. Equivalence of variances of latent variables H 0: PSI-1[1] = PSI-1[2] • This test will depend upon which ref. indicator used 2. Equivalence of error variances * 3. 4. H 0: Theta-eps[1] = Theta-eps[2] {entire matrix} df=3 *and covariances if there are correlated errors From last Friday 4

Multiple Group Models n Measurement model equivalence does not imply same mean levels ¨ Measurement model for Group 1 can be identical to Group 2, yet the two groups can differ radically in terms of level. Group 1 Group 2 Load mean n Always trust gov’t. 80 2. 3. 78 3. 9 n Govern. Corrupt -. 75 3. 8 -. 80 2. 3 n Politicians don’t care (where 1=agree strongly through 10=disagree strongly) n Example: From last Friday 5

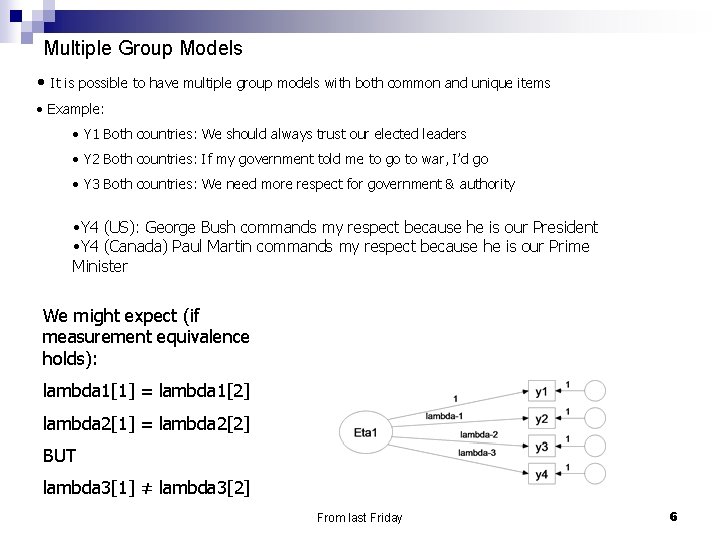
Multiple Group Models • It is possible to have multiple group models with both common and unique items • Example: • Y 1 Both countries: We should always trust our elected leaders • Y 2 Both countries: If my government told me to go to war, I’d go • Y 3 Both countries: We need more respect for government & authority • Y 4 (US): George Bush commands my respect because he is our President • Y 4 (Canada) Paul Martin commands my respect because he is our Prime Minister We might expect (if measurement equivalence holds): lambda 1[1] = lambda 1[2] lambda 2[1] = lambda 2[2] BUT lambda 3[1] ≠ lambda 3[2] From last Friday 6

Multiple Group Models • Should be careful with the use of reference indicators (and/or sensitive to the fact that apparently non-equivalent models might appear to be so simply because of a single (reference) indicator • Example: Group 1 Group 2 Lambda-1 1. 0* Lambda-2 . 50 1. 0 Lambda-3 . 75 1. 5 Lambda-4 1. 0 2. 0 • These two groups appear to have measurement models that are very different, but…. From last Friday 7

Multiple Group Models Group 1 Group 2 Lambda-1 1. 0* Lambda-2 . 50 1. 0 Lambda-3 . 75 1. 5 Lambda-4 1. 0 2. 0 • These two groups appear to have measurement models that are very different, but…. If we change the reference indicator to Y 2, we find: Gr 1 Gr 2 Lambda 1 2. 0 1. 0 Lambda 2 1. 0* Lambda 3 1. 5 Lambda 4 2. 0 From last Friday 8

Multiple Group Models Modification Indices and what they mean in multiple-group models Assuming LY[1] = LY[2] (entire matrix) Example: MODIFICATION INDICES: Group 1 Group 2 Eta 1 Y 1 --- Y 2 . 382 Y 3 1. 24 Y 4 45. 23 From last Friday 9

Multiple Group Models Modification Indices and what they mean in multiple-group models Assuming LY[1] = LY[2] (entire matrix) Example: MODIFICATION INDICES: Group 1 Group 2 Eta 1 Y 1 --- Y 2 . 382 Y 3 1. 24 Y 4 45. 23 Improvement in chisquare if equality constraint released 10

Multiple Group Models : Modification Indices MODIFICATION Group 1 Group 2 INDICES eta 1 eta 2 Y 1 Y 2 Y 3 --1. 42 0. 43 2. 42 3. 44 2. 11 --1. 42 0. 43 3. 89 1. 01 40. 89 Y 4 0. 11 --- 0. 98 --- Y 5 2. 32 1. 49 1. 22 1. 49 Y 6 1. 01 29. 23 3. 21 29. 23 Tests equality constraint lambda 5[1]=lambda 5[2] 11

Multiple Group Models : Modification Indices MODIFICATION Group 1 Group 2 INDICES eta 1 eta 2 Y 1 Y 2 Y 3 --1. 42 0. 43 2. 42 3. 44 2. 11 --1. 42 0. 43 3. 89 1. 01 40. 89 Y 4 0. 11 --- 0. 98 --- Y 5 2. 32 1. 49 1. 22 1. 49 Y 6 1. 01 29. 23 3. 21 29. 23 Tests equality constraint lambda 5[1]=lambda 5[2] Wald test (MI) for adding parameter LY(3, 3) to the model in group 2 only 12

MULTIPLE GROUP MODELS: parameter significance tests n n n When a parameter is constrained to equality across 2 (or more) groups, “pooled” significance test (more power) Possible to have a coefficient non-signif. in each of 2 groups yet significant when equality constraint imposed Possible to have a coefficient that is not significant in each of two groups (e. g. , +ve coefficient, NS, in one group, -ve, NS, in another) yet the difference between the groups is statistically significant 13

Tests in 3+ groups n n 2 -group model can be extended to m groups (in theory, infinite number as long as minimum sample size requirements met in each group; in practice, some software packages have limits) Models: ¨ ¨ ¨ n Group 1=Group 2=Group 3 Group 1=Group 2≠Group 3 Group 1 ≠ Group 2≠Group 3 Must be careful about interpretation of Modification Indices ¨ In a model with [1]=[2]=[3] ≠ 0, then a MI will provide an indication of how much the model improve if the parameter constraint is removed in the mth group only (e. g. , MI in group 2 would test against a model in which the group 1 & group 3 {same} parameter are constrained to equality but the group 2 is allowed to differ) 14

MULTIPLE GROUP MODELS: Modification Indices (again) Group 1 MOD INDICES Lambda 1 3. 01 Lambda 2 1. 52 Lambda 3 3. 22 Model: LY[1]=LY[2]=LY[3] Group 2 MOD INDICES Lambda 1 4. 22 Lambda 2 3. 99 Lambda 3 5. 22 Group 3 MOD INDICES Free LY(2, 1) in group 3 but Lambda 1 89. 22 Lambda 2 6. 11 LY(2, 1) in group 1 = LY(2, 1) in group 2 Lambda 3 1. 22 15

When do we have measurement equivalence n STRONG equivalence: all matrices identical, all groups ¨ (might possibly exclude variance of LV’s from this … i. e. , the PHI or PSI matrices) ¨ n WEAKER equivalence (usually accepted) ¨ Lambda matices identical, all groups ¨ Theta matrices could be different (and probably are), either having the same form or not n WEAKER YET: ¨ Lambda matrices have the same form, some identical coefficients 16

Measurement coefficients, construct equation coefficients in multiple group models n We usually need the measurement equation coefficients to be equivalent in order to proceed with comparison of construct equation coefficients 17

Measurement coefficients, construct equation coefficients in multiple group models n n We usually need the measurement equation coefficients to be equivalent in order to proceed with comparison of construct equation coefficients For this reason, tests for measurement equivalence are usually not as rigorous as the “substantive” tests for construct equation coefficient equivalence (though instances of poor fit should be noted in any report of results) 18

LISREL PROGRAMMING FOR MULTIPLE GROUP MODELS Basics: “Stack” the groups (one program after the next) In DA statement of first group, specify total number of groups: e. g. , DA NG=2 NI=23 NO=1246 NI specification (# of input var’s) applies only to group 1 NO specification (# of observations) applies only to group 1 19

LISREL PROGRAMMING FOR MULTIPLE GROUP MODELS DA NG=2 … Specify group 1 model as usual Title for Group 2 DA statement group 2 NI= NO= CM FI= [location of group 2 cov mtx] SE 13468/ LABELS [optional] MO NY= NX= NK= NE= + special options for matrix specification OU (as usual) 20

LISREL PROGRAMMING: MULTIPLE GROUPS MO specification: LY=PS same pattern as prev. group - for example, if group 1 specifies 2 LV’s with first three indicators on LV 1, next 6 on LV 2, this same specification will be copied to group 2 LY= IN invariant - same pattern and all free coefficients in this matrix constrained to equality with corresponding coefficients in previous group 21

LISREL PROGRAMMING: MULTIPLE GROUPS Adding equality constraints to a matrix that is otherwise allowed to differ from the same matrix in a previous group: Group 1 (e. g. ) LY=FU, FI VA 1. 0 LY 2 1 FR LY 2 1 LY 3 1 LY 4 1 Group 2 LY=PS EQ LY 1 2 1 LY 2 2 1 EQ LY 1 3 1 LY 3 1 22

LISREL PROGRAMMING: MULTIPLE GROUPS Releasing equality constraints on a single parameter when matrix is otherwise specified as Invariant: Group 2: LY=IN FR LY 4 1 LY remains invariant except for parameter LY(4, 1) 23

Examples: Example (separate handouts) n (religion & sexual morality in 2 countries) n Multiple group example #1: USA DA NO=1150 NI=19 MA=CM NG=2 CM FI=G: CLASSESICPSR 2005WEEK 3 EXAMPLESUSA. COV LA A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 GENDER AGE EDUC TOWNSIZE MARR 1 MARR 2 MARR 3 OCC 1 OCC 2 OCC 3 OCC 4 SE 1 2 3 4 5 6 7 8/ MO NY=8 NE=2 LY=FU, FI PS=SY, FR TE=SY Basic program VA 1. 0 LY 2 1 LY 5 2 FR LY 1 1 LY 3 1 LY 4 1 See handout for FR LY 6 2 LY 7 2 LY 8 2 variable list FR TE 4 3 24 OU ND=4 SC MI

Multiple group example #1: USA Number of Input Variables 19 Number of Y - Variables 8 Program & output: Number of X - Variables 0 Number of ETA - Variables 2 Two. Group 1 b. ls 8, *. out Number of KSI - Variables 0 Number of Observations 1150 Number of Groups 2 Group #2: Canada DA NO=1763 NI=19 MA=CM CM FI=G: CLASSESICPSR 2005WEEK 3 EXAMPLESCDN. COV LA A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 GENDER AGE EDUC TOWNSIZE MARR 1 MARR 2 MARR 3 OCC 1 OCC 2 OCC 3 OCC 4 SE 1 2 3 4 5 6 7 8/ MO LY=IN PS=PS TE=PS OU ND=4 SC MI Group #2: Canada Number of Input Variables 19 Number of Y - Variables 8 Number of X - Variables 0 Number of ETA - Variables 2 Number of KSI - Variables 0 Number of Observations 1763 Number of Groups 2 25

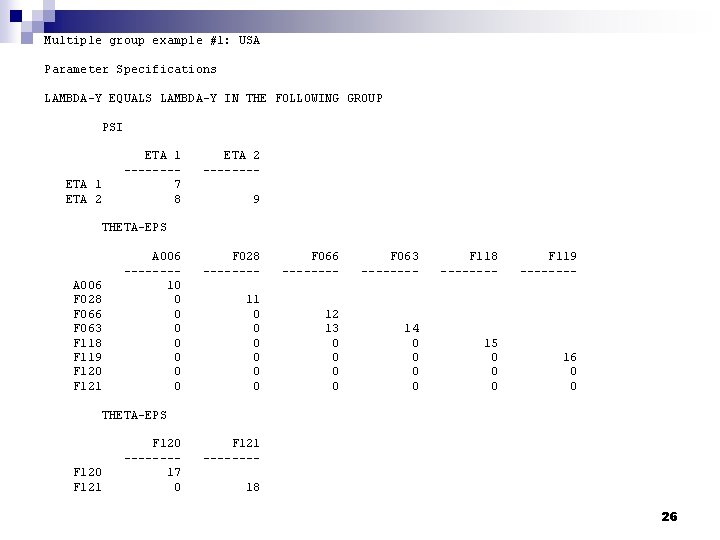
Multiple group example #1: USA Parameter Specifications LAMBDA-Y EQUALS LAMBDA-Y IN THE FOLLOWING GROUP PSI ETA 1 ETA 2 ETA 1 -------7 8 ETA 2 -------9 THETA-EPS A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 A 006 -------10 0 0 0 F 028 ---- F 066 ---- F 063 ---- F 118 ---- F 119 ---- 11 0 0 0 12 13 0 0 14 0 0 15 0 0 0 16 0 0 THETA-EPS F 120 F 121 F 120 -------17 0 F 121 -------18 26

Covariance Matrix of ETA 1 -------2. 4328 1. 9415 ETA 1 ETA 2 -------4. 5847 Group 1 PSI ETA 1 ETA 2 ETA 1 -------2. 4328 (0. 1554) 15. 6531 ETA 2 ---- 1. 9415 (0. 1464) 13. 2596 4. 5847 (0. 3118) 14. 7036 Covariance Matrix of ETA 1 -------3. 5419 2. 3997 ETA 1 ETA 2 -------5. 2741 PSI Group 2 ETA 1 ETA 2 ETA 1 -------3. 5419 (0. 1924) 18. 4093 ETA 2 ---- 2. 3997 (0. 1529) 15. 6932 5. 2741 (0. 3175) 16. 6128 27

Group Goodness of Fit Statistics (USA) Contribution to Chi-Square = 120. 0772 Percentage Contribution to Chi-Square = 51. 3912 Root Mean Square Residual (RMR) = 0. 2698 Standardized RMR = 0. 04414 Goodness of Fit Index (GFI) = 0. 9756 Global Goodness of Fit Statistics Degrees of Freedom = 42 Minimum Fit Function Chi-Square = 233. 6530 (P = 0. 0) Normal Theory Weighted Least Squares Chi-Square = 229. 0169 (P = 0. 0) Estimated Non-centrality Parameter (NCP) = 187. 0169 90 Percent Confidence Interval for NCP = (143. 2744 ; 238. 2786) Normed Fit Index (NFI) = 0. 9840 Non- Normed Fit Index (NNFI) = 0. 9824 Parsimony Normed Fit Index (PNFI) = 0. 7380 Comparative Fit Index (CFI) = 0. 9868 Incremental Fit Index (IFI) = 0. 9868 Relative Fit Index (RFI) = 0. 9787 Group Goodness of Fit Statistics (CANADA) Contribution to Chi-Square = 113. 5759 Percentage Contribution to Chi-Square = 48. 6088 Root Mean Square Residual (RMR) = 0. 2222 Standardized RMR = 0. 03069 Goodness of Fit Index (GFI) = 0. 9841 28

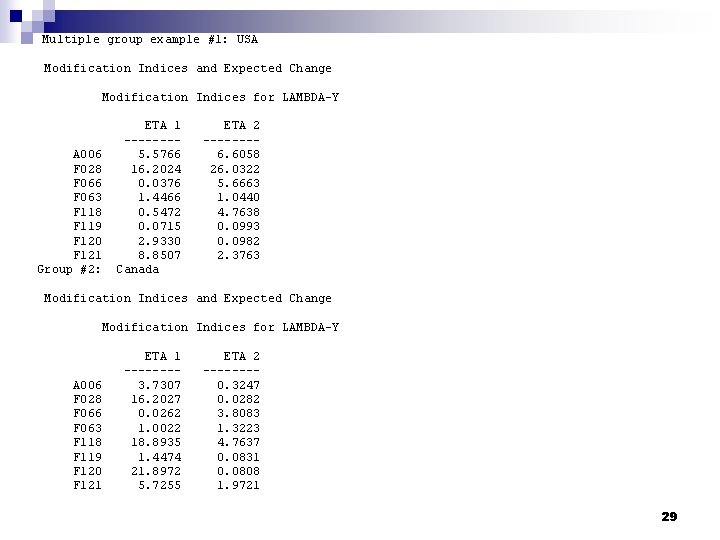
Multiple group example #1: USA Modification Indices and Expected Change Modification Indices for LAMBDA-Y A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 Group #2: ETA 1 -------5. 5766 16. 2024 0. 0376 1. 4466 0. 5472 0. 0715 2. 9330 8. 8507 Canada ETA 2 -------6. 6058 26. 0322 5. 6663 1. 0440 4. 7638 0. 0993 0. 0982 2. 3763 Modification Indices and Expected Change Modification Indices for LAMBDA-Y A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 ETA 1 -------3. 7307 16. 2027 0. 0262 1. 0022 18. 8935 1. 4474 21. 8972 5. 7255 ETA 2 -------0. 3247 0. 0282 3. 8083 1. 3223 4. 7637 0. 0831 0. 0808 1. 9721 29

LISREL Estimates (Maximum Likelihood) LAMBDA-Y A 006 ETA 1 -------0. 4590 (0. 0119) 38. 4181 F 028 1. 0000 - - F 066 0. 8854 (0. 0257) 34. 4187 - - F 063 -1. 1710 (0. 0332) -35. 2593 - - F 118 - - 1. 0000 F 119 - - 0. 7174 (0. 0262) 27. 3386 F 120 - - 1. 0684 (0. 0326) 32. 8141 F 121 - - ETA 2 ---- - 0. 7996 (0. 0267) 29. 9686 30

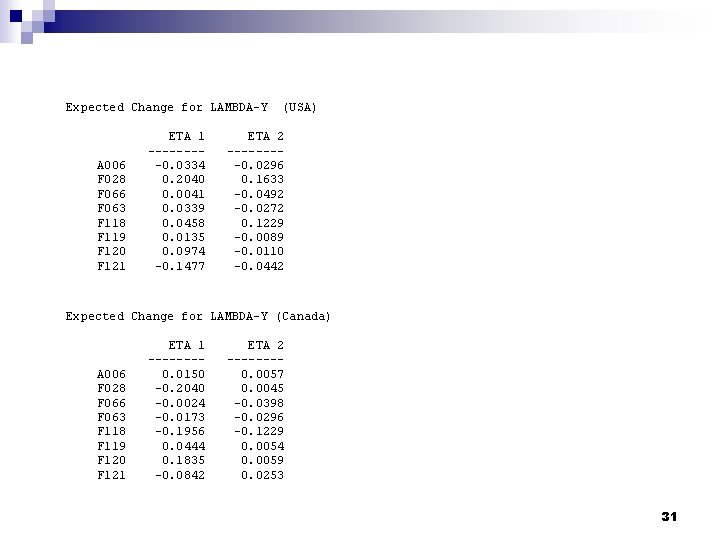
Expected Change for LAMBDA-Y A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 ETA 1 ----0. 0334 0. 2040 0. 0041 0. 0339 0. 0458 0. 0135 0. 0974 -0. 1477 (USA) ETA 2 ----0. 0296 0. 1633 -0. 0492 -0. 0272 0. 1229 -0. 0089 -0. 0110 -0. 0442 Expected Change for LAMBDA-Y (Canada) A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 ETA 1 -------0. 0150 -0. 2040 -0. 0024 -0. 0173 -0. 1956 0. 0444 0. 1835 -0. 0842 ETA 2 -------0. 0057 0. 0045 -0. 0398 -0. 0296 -0. 1229 0. 0054 0. 0059 0. 0253 31

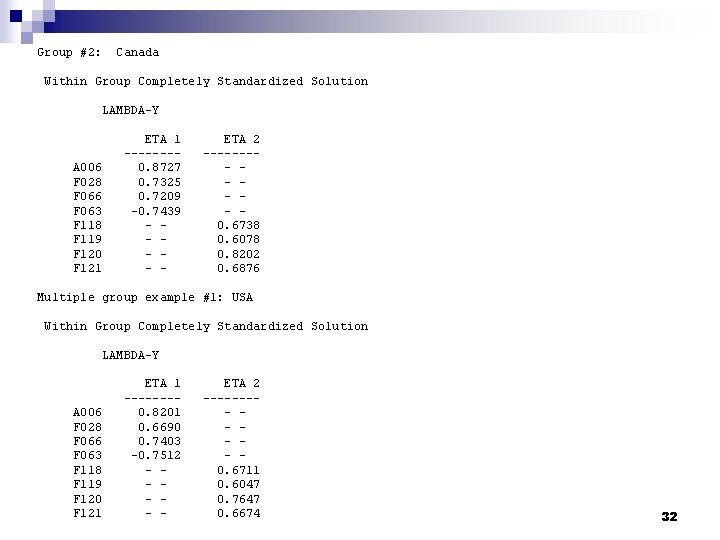
Group #2: Canada Within Group Completely Standardized Solution LAMBDA-Y A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 ETA 1 -------0. 8727 0. 7325 0. 7209 -0. 7439 - - - ETA 2 ---- - - - 0. 6738 0. 6078 0. 8202 0. 6876 Multiple group example #1: USA Within Group Completely Standardized Solution LAMBDA-Y A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 ETA 1 -------0. 8201 0. 6690 0. 7403 -0. 7512 - - - ETA 2 ---- - - - 0. 6711 0. 6047 0. 7647 0. 6674 32

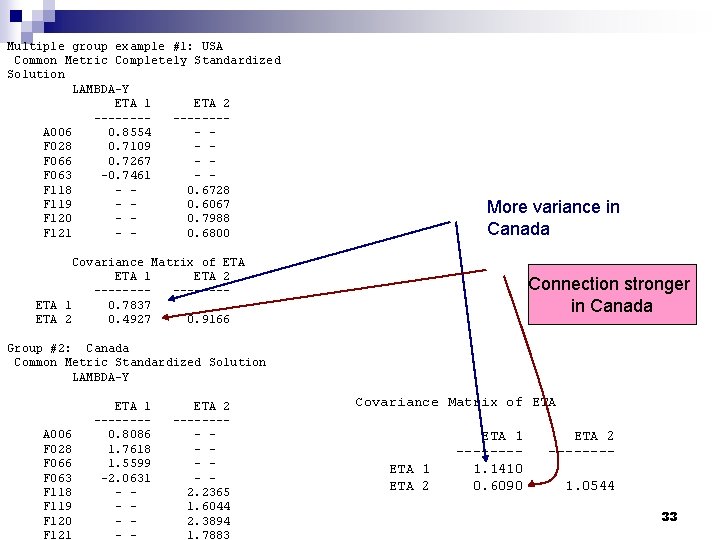
Multiple group example #1: USA Common Metric Completely Standardized Solution LAMBDA-Y ETA 1 ETA 2 -------A 006 0. 8554 - F 028 0. 7109 - F 066 0. 7267 - F 063 -0. 7461 - F 118 - 0. 6728 F 119 - 0. 6067 F 120 - 0. 7988 F 121 - 0. 6800 More variance in Canada Covariance Matrix of ETA 1 ETA 2 -------ETA 1 0. 7837 ETA 2 0. 4927 0. 9166 Connection stronger in Canada Group #2: Canada Common Metric Standardized Solution LAMBDA-Y A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 ETA 1 -------0. 8086 1. 7618 1. 5599 -2. 0631 - - - ETA 2 ---- - - - 2. 2365 1. 6044 2. 3894 1. 7883 Covariance Matrix of ETA 1 ETA 2 ETA 1 -------1. 1410 0. 6090 ETA 2 -------1. 0544 33

Testing measurement equivalence Group #2: Canada DA NO=1763 NI=19 MA=CM CM FI=G: CLASSESICPSR 2005WEEK 3 EXAMPLESCDN. COV LA A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 GENDER AGE EDUC TOWNSIZE MARR 1 MARR 2 MARR 3 OCC 1 OCC 2 OCC 3 OCC 4 SE 12345678/ MO LY=PS PS=PS TE=PS Global Goodness of Fit Statistics OU ND=4 SC MI Degrees of Freedom = 36 Minimum Fit Function Chi-Square = 209. 7783 (P = 0. 0) Normal Theory Weighted Least Squares Chi-Square = 207. 3408 (P = 0. 0) Estimated Non-centrality Parameter (NCP) = 171. 3408 90 Percent Confidence Interval for NCP = (129. 7727 ; 220. 4219) Normed Fit Index (NFI) = 0. 9856 Non-Normed Fit Index (NNFI) = 0. 9814 Parsimony Normed Fit Index (PNFI) = 0. 6336 Comparative Fit Index (CFI) = 0. 9881 Incremental Fit Index (IFI) = 0. 9881 Relative Fit Index (RFI) = 0. 9777 34

Some Model/Test Results: Matrices Chi-square Two. Group 1 b LY=IN 233. 653 42 Two. Group 1 c LY=PS 209. 778 36 Two. Group 1 d LY=IN PS=IN 272. 740 Two. Group 1 e LY=IN PS=IN but 267. 472 PS 2, 1 free df. 987. 988 45 44 IFI. 984. 985 From Two. Group 1 d, in Group #2 (Canada): Modification Indices for PSI ETA 1 ETA 2 -------ETA 1 31. 1069 ETA 2 4. 8672 4. 0391 Expected Change for PSI ETA 1 ETA 2 -------ETA 1 0. 3466 ETA 2 -0. 1158 0. 2188 35

Models with exogenous variables in construct equations: Multiple group example #1: USA DA NO=1150 NI=19 MA=CM NG=2 CM FI=G: CLASSESICPSR 2005WEEK 3 EXAMPLESUSA. COV LA A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 GENDER AGE EDUC TOWNSIZE MARR 1 MARR 2 MARR 3 OCC 1 OCC 2 OCC 3 OCC 4 SE 1 2 3 4 5 6 7 8 9 10 11 12/ MO NY=8 NE=2 LY=FU, FI PS=SY, FR TE=SY NX=4 NK=4 LX=ID C PH=SY, FR TD=ZE GA=FU, FR LE Group #2: Canada RELIG MORAL DA NO=1763 NI=19 MA=CM VA 1. 0 LY 2 1 LY 5 2 CM FI=G: CLASSESICPSR 2005WEEK 3 EXAMPLESCDN. COV FR LY 1 1 LY 3 1 LY 4 1 LA FR LY 6 2 LY 7 2 LY 8 2 A 006 F 028 F 066 F 063 F 118 F 119 F 120 F 121 GENDER FR TE 4 3 AGE EDUC TOWNSIZE MARR 1 MARR 2 MARR 3 OU ND=4 SC MI OCC 1 OCC 2 OCC 3 OCC 4 SE 1 2 3 4 5 6 7 8 9 10 11 12/ MO LY=IN PS=PS TE=PS LX=IN PH=PS TD=IN GA=PS LE RELIG MORAL OU ND=4 SC MI 36

LAMBDA-Y EQUALS LAMBDA-Y IN THE FOLLOWING GROUP GAMMA RELIG MORAL GENDER -------7 11 AGE -------8 12 EDUC -------9 13 TOWNSIZE -------10 14 AGE ---- EDUC ---- TOWNSIZE ---- 17 19 22 20 23 24 PHI GENDER AGE EDUC TOWNSIZE GENDER -------15 16 18 21 PSI RELIG MORAL RELIG -------25 26 MORAL -------27 37

Multiple group example #1: USA LISREL Estimates (Maximum Likelihood) LAMBDA-Y EQUALS LAMBDA-Y IN THE FOLLOWING GROUP GAMMA GENDER AGE EDUC TOWNSIZE --------------RELIG 0. 6772 -0. 0169 0. 0818 0. 0182 (0. 1001) (0. 0031) (0. 0351) (0. 0293) 6. 7629 -5. 5270 2. 3342 0. 6194 MORAL 0. 0671 -0. 0143 0. 3045 (0. 1451) (0. 0045) (0. 0515) 0. 4623 -3. 1968 5. 9077 Group #2: Canada Number of Iterations = 8 LISREL Estimates (Maximum Likelihood) GAMMA GENDER AGE EDUC -----------RELIG 0. 9517 -0. 0292 0. 1184 (0. 0926) (0. 0028) (0. 0397) 10. 2755 -10. 4921 2. 9799 MORAL -0. 0967 (0. 1182) -0. 8176 -0. 0222 (0. 0036) -6. 1962 0. 4775 (0. 0526) 9. 0759 -0. 0218 (0. 0428) -0. 5080 TOWNSIZE -------0. 0636 (0. 0173) 3. 6641 0. 0934 (0. 0226) 4. 1312 38

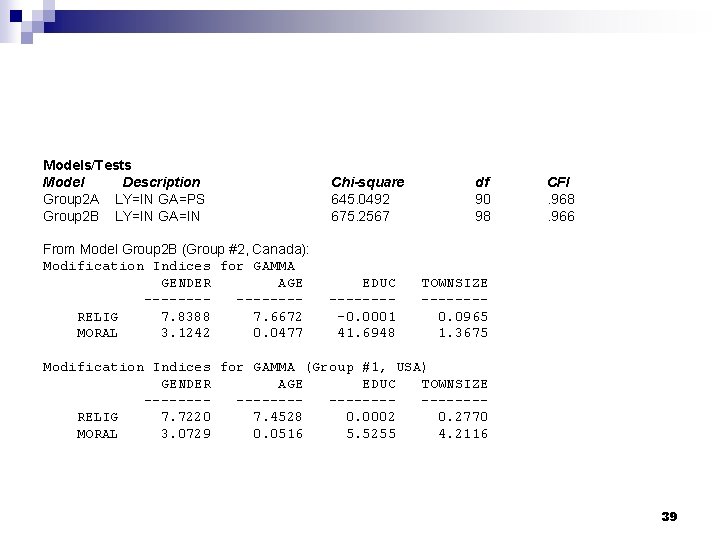
Models/Tests Model Description Group 2 A LY=IN GA=PS Group 2 B LY=IN GA=IN Chi-square 645. 0492 675. 2567 From Model Group 2 B (Group #2, Canada): Modification Indices for GAMMA GENDER AGE -------RELIG 7. 8388 7. 6672 MORAL 3. 1242 0. 0477 EDUC ----0. 0001 41. 6948 df 90 98 CFI. 968. 966 TOWNSIZE -------0. 0965 1. 3675 Modification Indices for GAMMA (Group #1, USA) GENDER AGE EDUC TOWNSIZE --------------RELIG 7. 7220 7. 4528 0. 0002 0. 2770 MORAL 3. 0729 0. 0516 5. 5255 4. 2116 39

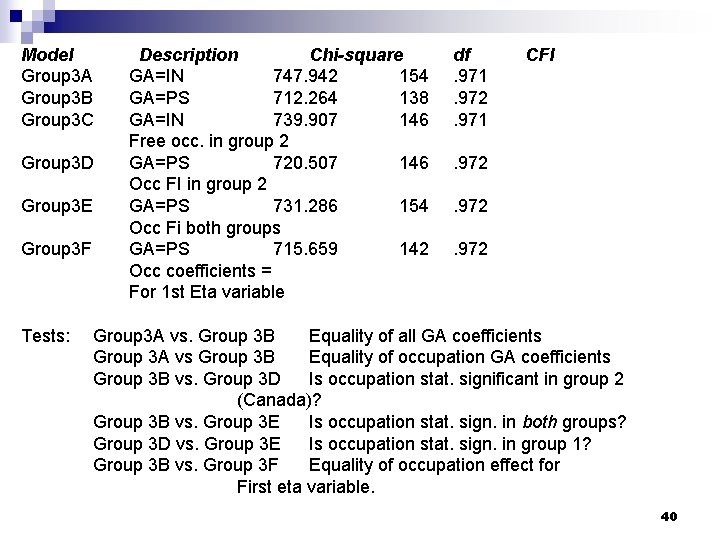
Model Group 3 A Group 3 B Group 3 C Group 3 D Group 3 E Group 3 F Tests: Description Chi-square GA=IN 747. 942 154 GA=PS 712. 264 138 GA=IN 739. 907 146 Free occ. in group 2 GA=PS 720. 507 146 Occ FI in group 2 GA=PS 731. 286 154 Occ Fi both groups GA=PS 715. 659 142 Occ coefficients = For 1 st Eta variable df. 971. 972. 971 CFI . 972 Group 3 A vs. Group 3 B Equality of all GA coefficients Group 3 A vs Group 3 B Equality of occupation GA coefficients Group 3 B vs. Group 3 D Is occupation stat. significant in group 2 (Canada)? Group 3 B vs. Group 3 E Is occupation stat. sign. in both groups? Group 3 D vs. Group 3 E Is occupation stat. sign. in group 1? Group 3 B vs. Group 3 F Equality of occupation effect for First eta variable. 40

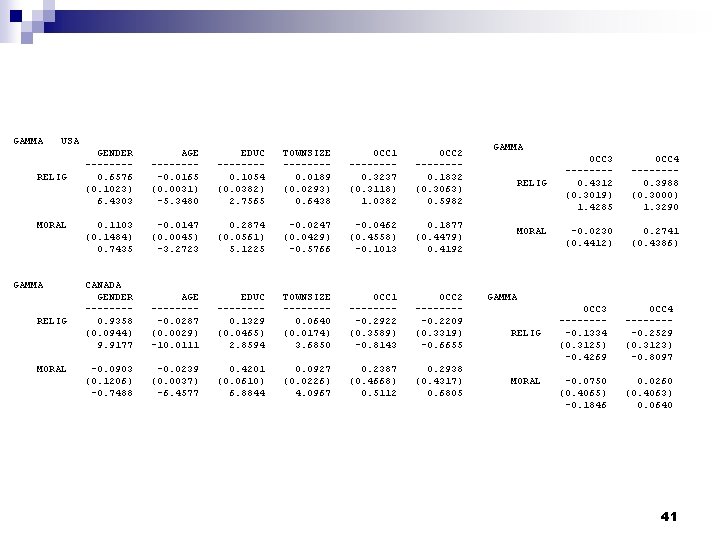
GAMMA USA RELIG MORAL GAMMA RELIG MORAL GENDER -------0. 6576 (0. 1023) 6. 4303 AGE ----0. 0165 (0. 0031) -5. 3480 EDUC -------0. 1054 (0. 0382) 2. 7565 TOWNSIZE -------0. 0189 (0. 0293) 0. 6438 OCC 1 -------0. 3237 (0. 3118) 1. 0382 OCC 2 -------0. 1832 (0. 3063) 0. 5982 0. 1103 (0. 1484) 0. 7435 -0. 0147 (0. 0045) -3. 2723 0. 2874 (0. 0561) 5. 1225 -0. 0247 (0. 0429) -0. 5766 -0. 0462 (0. 4558) -0. 1013 0. 1877 (0. 4479) 0. 4192 CANADA GENDER -------0. 9358 (0. 0944) 9. 9177 AGE ----0. 0287 (0. 0029) -10. 0111 EDUC -------0. 1329 (0. 0465) 2. 8594 TOWNSIZE -------0. 0640 (0. 0174) 3. 6850 OCC 1 ----0. 2922 (0. 3589) -0. 8143 OCC 2 ----0. 2209 (0. 3319) -0. 6655 -0. 0903 (0. 1206) -0. 7488 -0. 0239 (0. 0037) -6. 4577 0. 4201 (0. 0610) 6. 8844 0. 0927 (0. 0226) 4. 0967 0. 2387 (0. 4668) 0. 5112 0. 2938 (0. 4317) 0. 6805 GAMMA RELIG MORAL OCC 3 -------0. 4312 (0. 3019) 1. 4285 OCC 4 -------0. 3988 (0. 3000) 1. 3290 -0. 0230 (0. 4412) 0. 2741 (0. 4386) GAMMA RELIG MORAL OCC 3 ----0. 1334 (0. 3125) -0. 4269 OCC 4 ----0. 2529 (0. 3123) -0. 8097 -0. 0750 (0. 4065) -0. 1846 0. 0260 (0. 4063) 0. 0640 41

(insert AMOS demo here) 42