Frelsning 4 5 Logik med tillmpningar 97 11

Föreläsning 4 -5 Logik med tillämpningar 97 -11 -11

F 4 -5 Innehåll u Deduktiva – – system Gentzensystem Hilbertsystem u Resolution u Kapitel 2. 7 - 2. 10 i Ben-Ari u Efter dagens föreläsning kan hela laboration 1 lösas.

F 4 -5 u Semantiska tablåer kontrollerar en given formels satisfierbarhet. Den ”uppfinner” inga nya formler och utnyttjar inte några antaganden. u En teoretiker har som uppgift att hitta på en mängd intressanta axiom, från vilka han/hon sedan kan härleda teorem. u I våra termer härleder teoretikern element ur T(U) för att hitta logiska konsekvenser av axiomen U. Definition (2. 5. 14) Låt T(U) = {A | U A}. T(U) kallas teorin av U och elementen i T(U) kallas teoremen av U. Elementen i U kallas axiomen av T(U). Teorem (2. 5. 11) Vi har visat att A T(U) omm (A 1 . . . An) A är valid där U = {A 1, . . . , An}.

F 4 -5 Problem: u Mängden axiom behöver inte vara ändlig. u Inte alla logiska system har beslutsprocedurer för validitet som satslogiken. u En algoritm för validitet ger liten insikt i strukturen av beviset. u Vi har svårt att använda strukturen i ett bevis för att göra ett nytt bevis för en liknande formel.

F 4 -5 Deduktiva bevis u Välj – en mängd axiom och – en mängd regler för hur man får dra slutsaster u Slutsatser som man drar bildar teorem och beskrivningen av hur man nått teoremet kallas beviset för teoremet.

F 4 -5 Skillnaden mellan semantiska och deduktiva system: u Semantiska system kräver inte att vi är smarta, bevisen är mekaniska. u Deduktiva system kräver att vi planerar vårt bevis, och att vi har viss erfarenhet. De är sämre för datorer.

F 4 -5 Hilbert och Gentzen 1862 -1943 ”Wir müssen wissen, wir werden wissen. ” - Vi måste veta, vi ska veta. 1909 -1945 Blev Hilberts assistent 1934 Dog av undernäring i ryskt fångenskap u Hilbert-system – har flera axiom men bara en regel. – formaliserar klassiska metoder för matematiskt resonerande u Gentzen-system – har ett axiom men många regler. – är lättare än Hilbert-system att mekanisera

F 4 -5 Gentzensystem u Brukar betecknas G och kallas även naturlig deduktion. u Använder mängder av formler, precis som de semantiska tablåerna.

F 4 -5 Definition (2. 8. 1) Systemet G består av axiom och inferensregler. Ett axiom i G är en mängd formler U innehållande ett kompletterande par av literaler. Inferensreglerna har formen Premisser och Slutsatser

F 4 -5

F 4 -5 Bevis och bevisbarhet Definition (2. 8. 2) Ett bevis i G är en sekvens av formelmängder så att varje element antingen är ett axiom eller kan härledas från en eller två tidigare element i sekvensen med hjälp av en inferensregel. Om A är sista elementet i en sådan sekvens, så kallas sekvensen för ett bevis av A, och A är bevisbar. Notation: A.

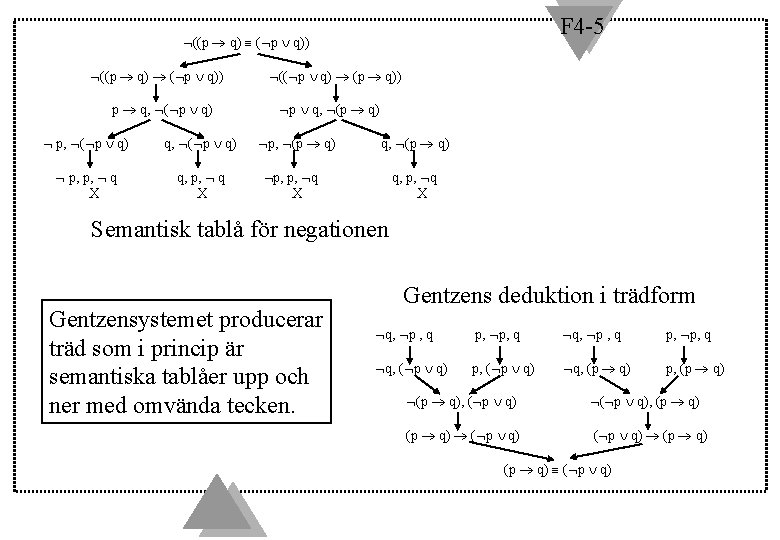
F 4 -5 ((p q) ( p q)) p q, ( p q) p, ( p q) q, ( p q) p, p, q X q, p, q X (( p q) (p q)) p q, (p q) p, (p q) q, (p q) p, p, q X q, p, q X Semantisk tablå för negationen Gentzensystemet producerar träd som i princip är semantiska tablåer upp och ner med omvända tecken. Gentzens deduktion i trädform q, p , q p, p, q q, ( p q) p, ( p q) q, (p q) p, (p q), ( p q), (p q) ( p q)

F 4 -5 Är systemet korrekt? u För att visa validitet med semantiska tablåer var vi tvungna att negera formeln och visa att den inte är satisfierbar. u Gentzensystemet gör precis detta, fast bakvägen. u Vi kan därför lätt visa att Gentzensystemet är sunt och fullständigt med hjälp av resultaten från semantiska tablåerna.

F 4 -5 Teorem (2. 8. 5) (bevisas i boken) u Låt U vara en mängd formler och låt U' vara mängden av komplementen till formlerna i U. Det finns ett bevis för U i G om det finns en stängd semantisk tablå för U'. u Specialfall: Det finns ett bevis för A i G omm den semantiska tablån för A är stängd.

F 4 -5 Sundhet och fullständighet för G Teorem (2. 8. 6) En formel A är valid omm A är bevisbar i G. Bevis: A är valid omm A är osatisfierbar omm den semantiska tablån för A är stängd omm det finns ett bevis för A i G.

Hilbertsystem u Hilbertsystemet F 4 -5 har tre axiom och en inferensregel u Axiomen definierar en oändlig mängd axiom, eftersom A, B och C representerar godtyckliga formler. Definition (2. 9. 1) För godtyckliga formler A, B och C så är följande formler axiom i H: (A (B A)) ((A (B C)) ((A B) (A C)) ( B A) (A B)

F 4 -5 Inferensregeln Definition (2. 9. 2) För godtyckliga formler A och B så är inferensregeln i H. Denna regel kallas för modus ponens eller MP.

F 4 -5 Härledda inferensregler u Vi kan utöka Hilbertsystem med s k härledda inferensregler. Vi kan då använda dessa regler precis som vi använder modus ponens. u Vi måste kunna visa att den nya regeln är sund. u Detta görs genom att visa hur ett bevis som använder den nya regeln kan transformeras till ett nytt bevis som bara använder MP.

F 4 -5 Antaganden (assumptions) Definition (2. 9. 4) Låt U vara en mängd formler och A en formel. Notationen U A betyder att formlerna i U är antaganden i beviset av A, dvs, de kan användas precis som axiomen i bevisföringen.

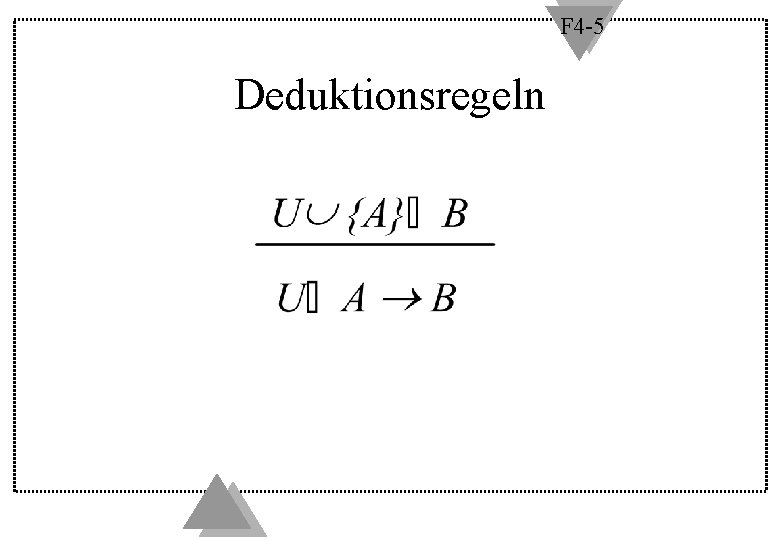
F 4 -5 Deduktionsregeln

F 4 -5 Kontrapositiva regeln

F 4 -5 Tranisitivitets regeln Detta teorem visar att det är OK att visa ett teorem med hjälp av en serie lemman.

F 4 -5 Byte av antecedenter Det spelar ingen roll i vilken ordning man gör sina antaganden.

F 4 -5 Dubbla negeringsregeln u Vanligt resonemang i – Om inte x y så är x = y matematik. u Kan vara lurigt att använda i dagligt tal… – ”Det är inte sant att jag inte är glad” behöver inte vara samma sak som ”Jag är glad”.

F 4 -5 Är Hilbertsystemet korrekt? u Sundhet: Om A så gäller att A. Dvs om A är bevisbar så ska A vara valid. – Visas genom att visa att axiomen är valida (med semantiska tablåer) och sedan göra ett motbevis. Vi antar att Modus Ponens inte är valid och når en motsägelse. u Fullständighet: Om A så gäller att A. Dvs om A är valid så ska A vara bevisbar. – Utnyttjar att vi bevisat fullständighet hos Gentzen-system och visar hur ett bevis i G transformeras till ett i H.

F 4 -5 Exempel q q p ( p q) ( q p) up (p q) p (p q)) p ( p q)) p up

F 4 -5 Resolution u Resolution lämpar sig ypperligt för att implementera automatisk bevissökning på dator. u Resolution är förhållandevis effektivt. bildar den teoretiska basen för logikprogrammering.

CNF F 4 -5 Definition (2. 10. 1) En formel är i konjunktiv normalform (CNF) om den är en konjunktion av disjunktioner av literaler. ( p q) ( r) (p) ( p q) ((p q) r) (p) ( p q) ( r p) Teorem (2. 10. 2) Alla satslogiska formler kan omvandlas till konjunktiv normalform.

F 4 -5 Klausul, klausulform, enhetsklausul u Klausul = mängd med literaler u Formel = mängd med klausuler u Man säger att en formel enligt ovan är i klausulform u Enhetsklausul = en klausul med endast en literal u En formel i klausulform är satisfierbar omm motsvarande CNF-formel är satisfierbar.

F 4 -5 Förkortad skrivform Formler i klausulform tex: ( p q r) ( r) skrivs som Notera att negation markeras med ett streck över symbolen.

F 4 -5 Transformationer av formler Definition (2. 10. 4) Låt S och S' vara klausulmängder. S S' betyder att S är satisfierbar omm S' är satisfierbar. Vi kommer att titta på flera lemman där man kan transformera formlerna till en ny mängd utan att förändra satisfierbarheten.

F 4 -5 u. I följande lemman och teorem kommer S vara klausulmängder, C klausuler och l literaler. Om l är en literal, så är lc dess komplement. u Lemma (2. 10. 5) Antag att en literal l finns i S, men inte lc. Låt S' vara klausalmängden där alla klausuler som innehåller l tagits bort. Då gäller S S'.

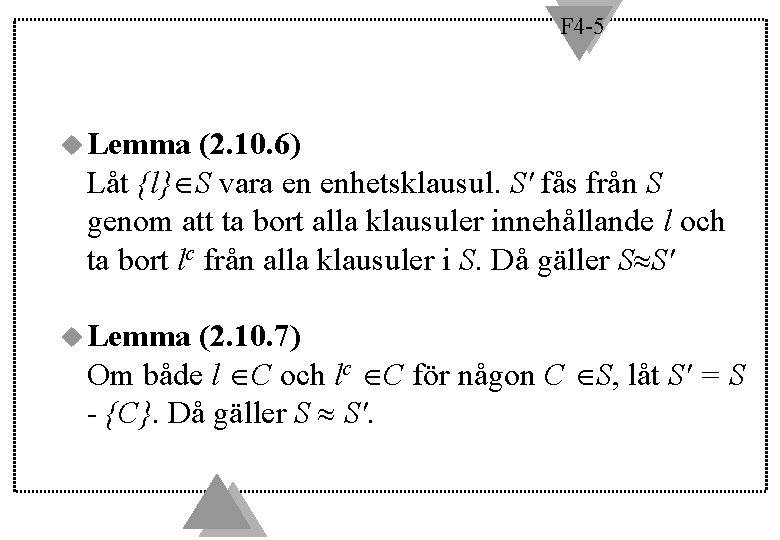
F 4 -5 u Lemma (2. 10. 6) Låt {l} S vara en enhetsklausul. S' fås från S genom att ta bort alla klausuler innehållande l och ta bort lc från alla klausuler i S. Då gäller S S' u Lemma (2. 10. 7) Om både l C och lc C för någon C S, låt S' = S - {C}. Då gäller S S'.

F 4 -5 Subsumering u Definition (2. 10. 8) Om C 1 C 2, så säger vi att C 1 subsumerar C 2, och C 2 är subsumerad av C 1. u Lemma 2. 10. 9 Om C 1, C 2 S och C 1 subsumerar C 2, låt S' = S - {C 2}. Då gäller S S', dvs den större klausulen kan tas bort.

F 4 -5 Tomma mängder av klausuler u Antag S=. S är uppenbart valid, dvs de möjliga interpretationerna v(p) = T och v(p) = F satisfierar båda S. u Enligt lemma (2. 10. 7) så kan vi ta bort alla klausuler som innehåller kompletterande literaler utan att påverka satisfierbarheten. S' = {} = , dvs tomma mängden. u En tom klausulmängd är alltså satisfierbar.

F 4 -5 Tomma klausuler S = {p, }. S är ekvivalent med p p, en formel som är uppenbart osatisfierbar. u Enligt lemma (2. 10. 6) kan vi ta bort en enhetsklausul och samtidigt ta bort alla komplement till literalen ur kvarvarande klausuler i S utan att påverka satisfierbarheten. Vi får då S' = { }, där står för den tomma klausulen. u En klausulmängd innehållande en tom klausul är alltså inte satisfierbar. u Antag

F 4 -5 Resolutionsregeln C 1 och C 2 vara klausuler så att l C 1 och lc C 2. C 1 och C 2 är då kolliderande (clashing) klausuler och de kolliderar på de kompletterande literalerna l och lc. u Klausulen C = Res(C 1, C 2) = (C 1 - (l}) (C 2 - (lc }) kallas för resolventen av C 1 och C 2. u C 1 och C 2 är föräldraklausuler till C. u Låt

F 4 -5 Är resolventen satisfierbar? ? u Teorem (2. 10. 12) Resolventen C är satisfierbar omm föräldraklausulerna C 1 och C 2 är (ömsesidigt) satsifierbara.

F 4 -5 Resolutionsproceduren u Låt S vara en mängd klausuler och definiera S 0 = S. Antag att vi har konstruerat Si. Välj två kolliderande klausuler C 1, C 2 Si, och låt C vara resolventen Res(C 1, C 2). u Om C = kan proceduren avbrytas, eftersom S då är osatsifierbar. u Annars konstruera Si+1 = Si {C}. Om Si+1 = Si för alla möjliga kollisioner, avbryts proceduren, S är satisifierbar.

F 4 -5 u Resolution är inte en beslutsprocedur för validitet, utan för satisiferbarhet. Som vi vet sedan tidigare är detta inte ett problem. u För att avgöra om formeln A är valid, så kontrollerar vi om A är satisfierbar. Om A inte är satisfierbar, så är A valid. u Resolution u Det är alltså en refuteringsprocedur. normala användningssättet för resolution är att använda det för teorembevisning.