Finding Volumes Using Cross Sections Known Cross Sections









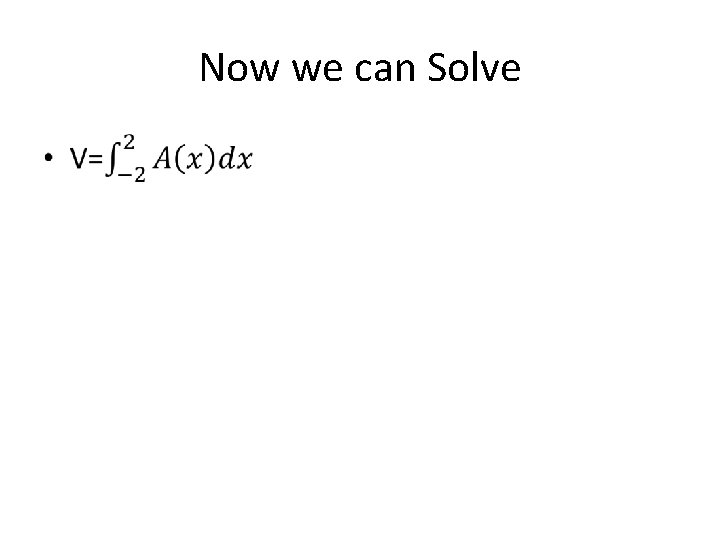
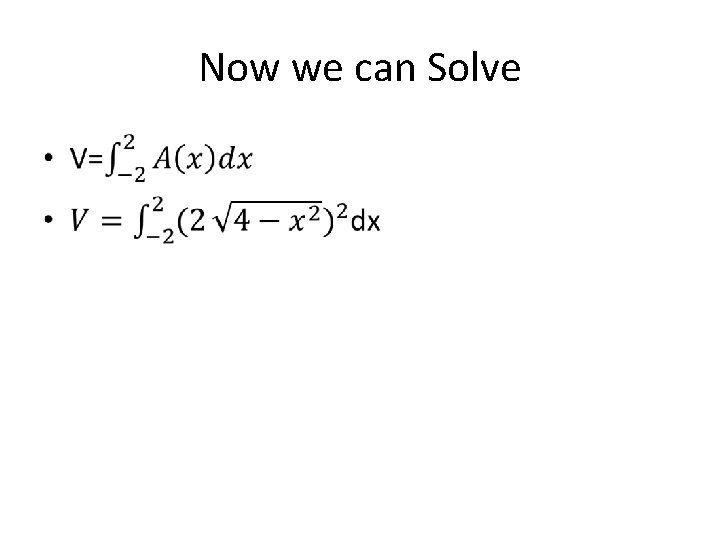
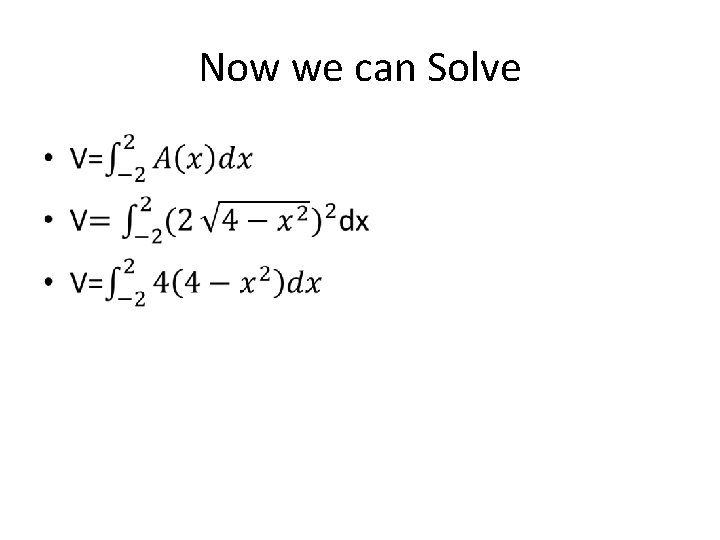
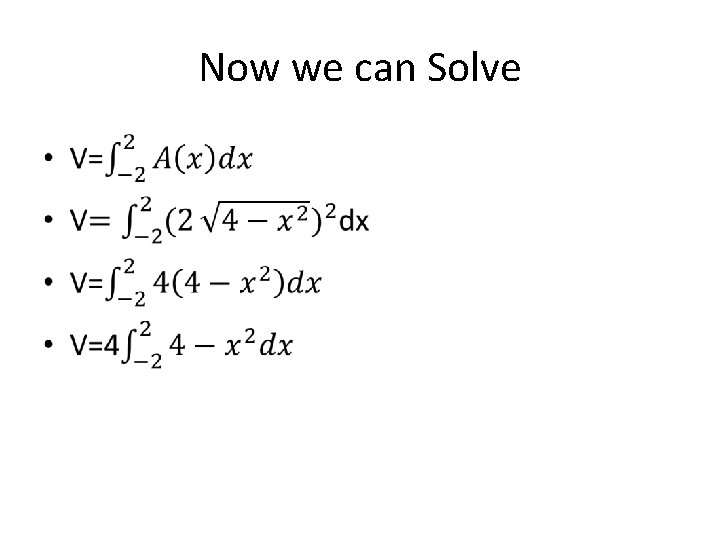
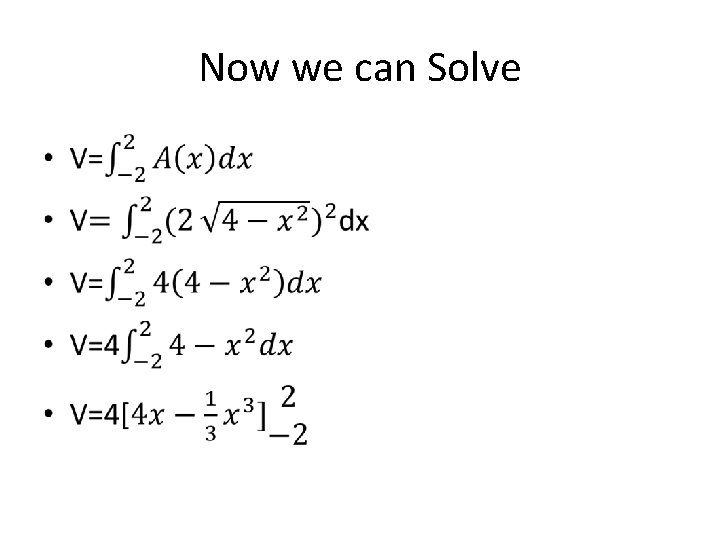
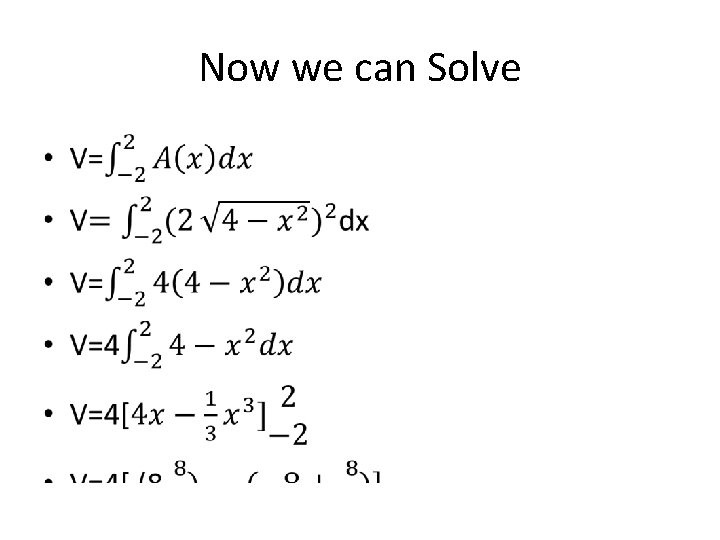
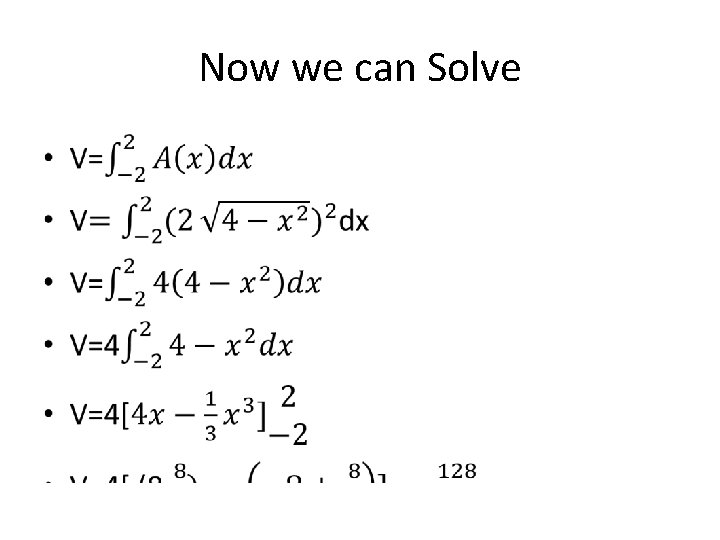





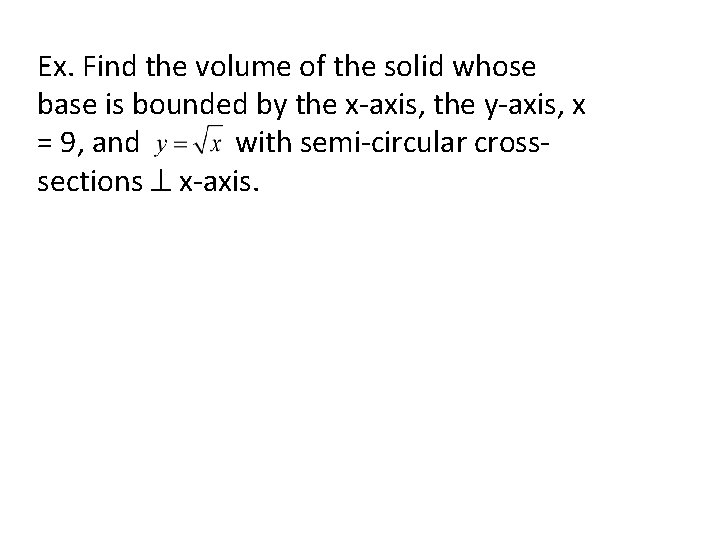

- Slides: 29

Finding Volumes Using Cross Sections

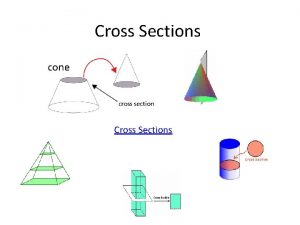
Known Cross Sections Method Volume can be calculated by finding area of known geometric shapes and multiplying by thickness (dx). Here is an example of squares stacked on top of a circular region.

We can find the area of each cross section, then add an infinite number of infinitely thin cross sections. When we multiply by thickness, we have volume.

Examples Cross sections may be rectangles, semicircles or triangles. The base of the solid may be a rectangle, circle, triangle or an irregular shape. Mathematica

Method of Slicing: 1 Sketch the base of the solid (including a typical slice) and a typical cross section. 2 Find a formula for A(x) and multiply by dx for width. 3 Find the limits of integration. Remember these MUST match the thickness of the cross section! 4 Integrate V(x) to find volume.

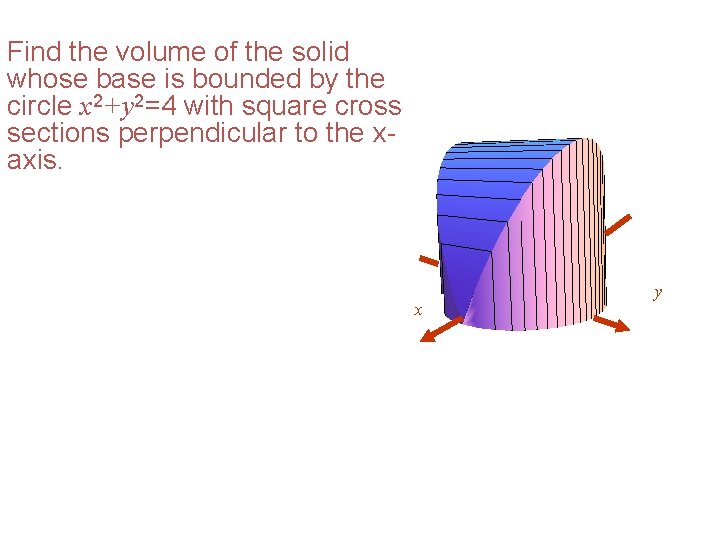
Find the volume of the solid whose base is bounded by the circle x 2+y 2=4 with square cross sections perpendicular to the xaxis. x y

Think about the base of the solid….

Think about the base of the solid…. It is a circle

Think about the base of the solid…. It is a circle

Think about the base of the solid…. It is a circle Think about the area of a square, A=s 2 and how you can write that in terms of the equation you are given for the base of the shape x 2 + y 2 = 4

Think about the base of the solid…. It is a circle Think about the area of a square, A=s 2 and how you can write that in terms of the equation you are given for the base of the shape x 2 + y 2 = 4 The side of the square is going to be 2 y if the squares are perpendicular to the x - axis

Think about the base of the solid…. It is a circle Think about the area of a square, A=s 2 and how you can write that in terms of the equation you are given for the base of the shape x 2 + y 2 = 4 The side of the square is going to be 2 y if the squares are perpendicular to the x – axis The thickness of the square is going to with respect to x

Think about the base of the solid…. It is a circle Think about the area of a square, A=s 2 and how you can write that in terms of the equation you are given for the base of the shape x 2 + y 2 = 4 The side of the square is going to be 2 y if the squares are perpendicular to the x – axis The thickness of the square is going to with respect to x So we need to get our original function in terms of x in order to write our integral

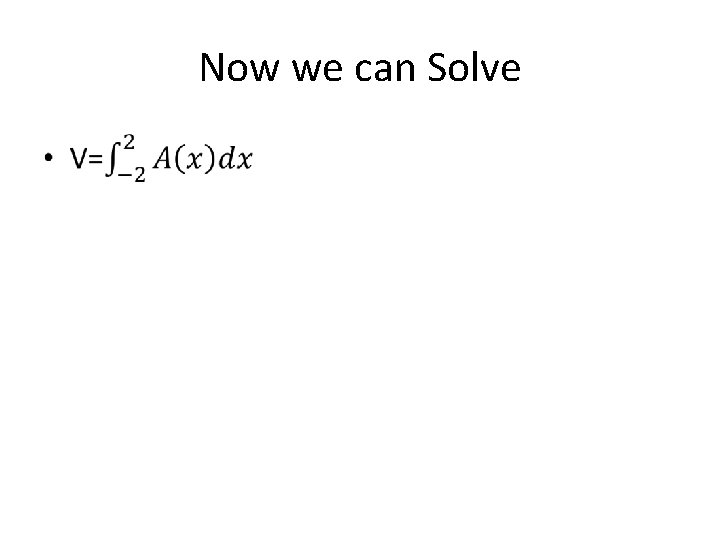
Now we can Solve •
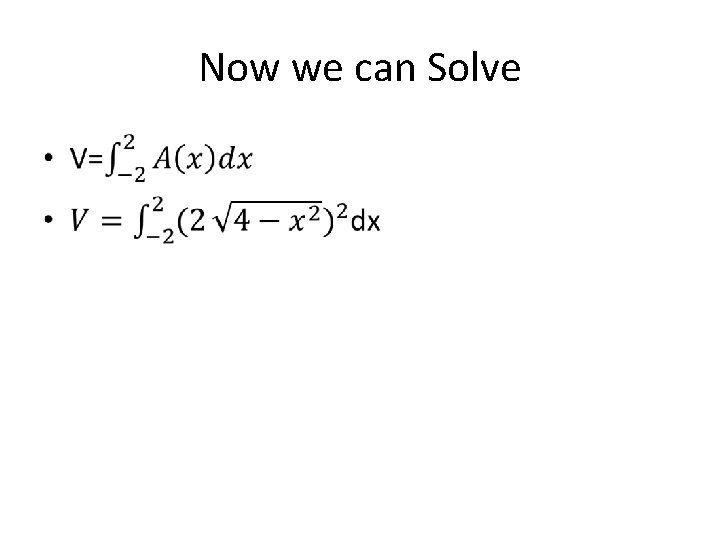
Now we can Solve •
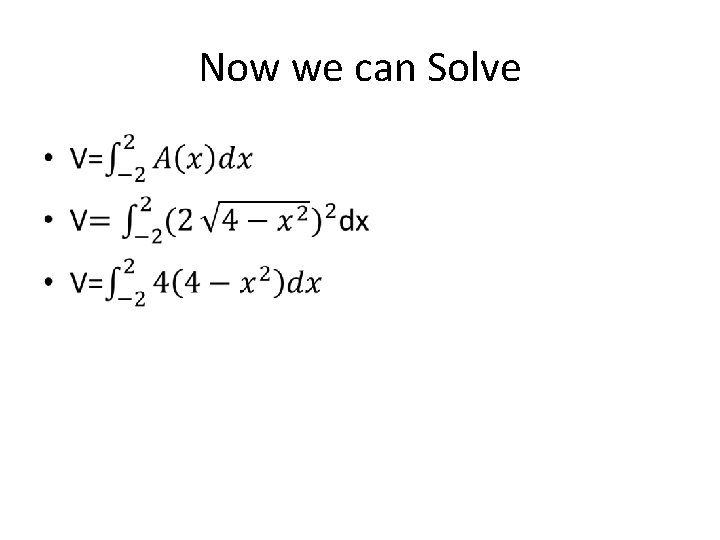
Now we can Solve •
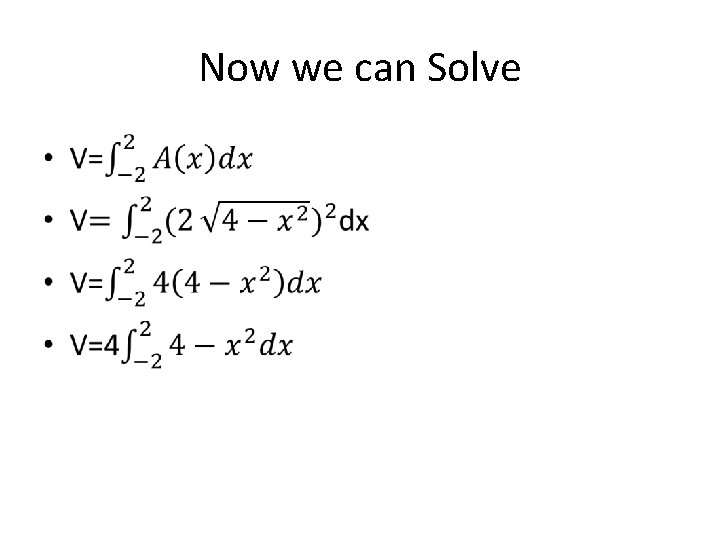
Now we can Solve •
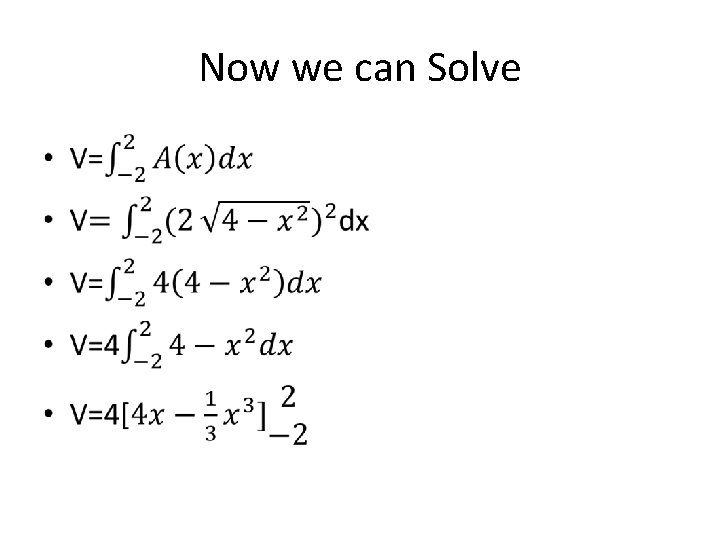
Now we can Solve •
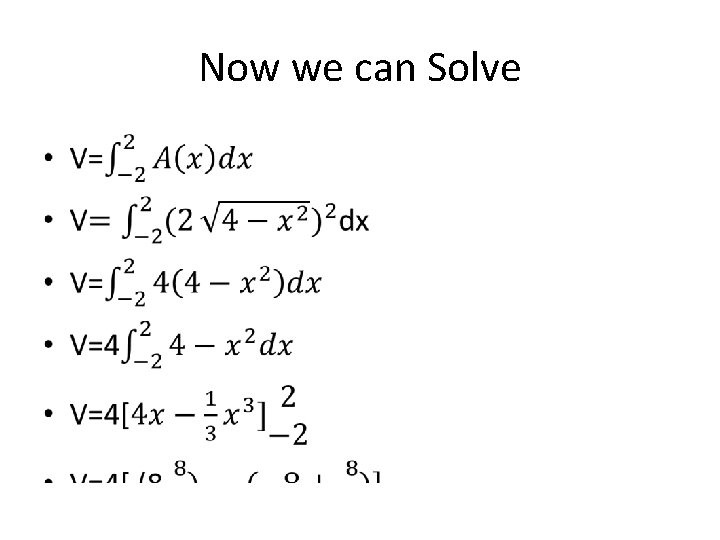
Now we can Solve •
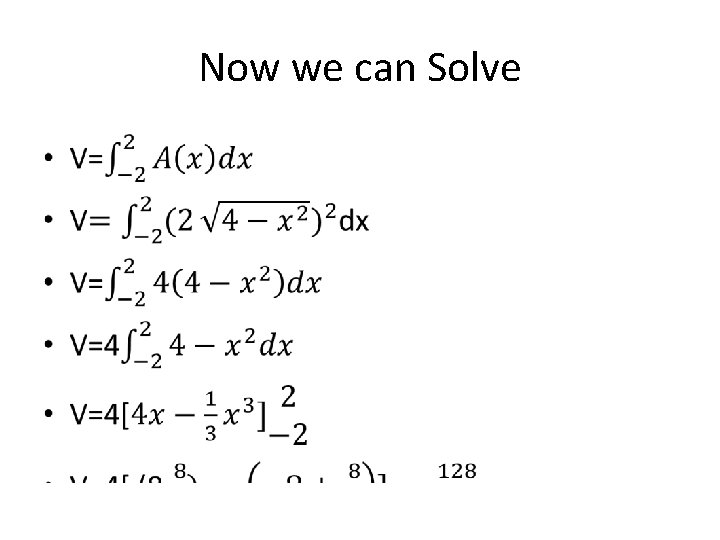
Now we can Solve •

Find the volume of the pyramid: Consider a horizontal slice through the pyramid. 3 The volume of the slice is s 2 dh. If we put zero at the top of the pyramid and 3 3 make down the positive direction, then s=h. 0 h s 3 dh This correlates with the formula:

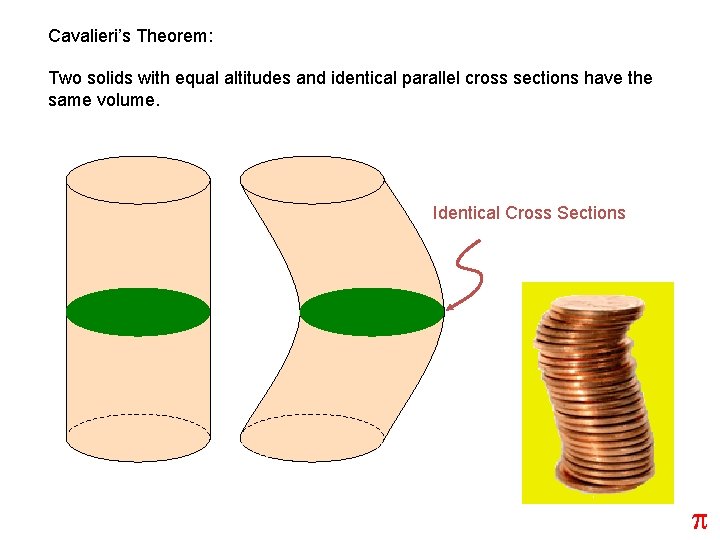
Cavalieri’s Theorem: Two solids with equal altitudes and identical parallel cross sections have the same volume. Identical Cross Sections p

Find the volume of the solid whose base is bounded by the circle x 2+y 2=4 with semicircular cross sections perpendicular to the x-axis x y

Find the volume of the solid whose base is bounded by the circle x 2+y 2=4 with equilateral triangle cross sections perpendicular to the x-axis. x y

Find the volume of the solid formed with the region defined by and as the base and cross sections that are squares perpendicular to the base and the x-axis.

Ex. Find the volume of the solid whose base is a circle of radius 1 in the first quadrant and with square cross-sections x-axis.
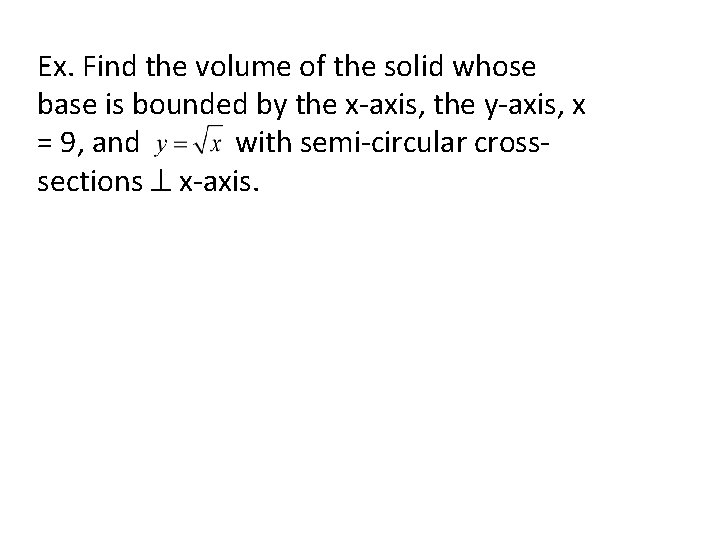
Ex. Find the volume of the solid whose base is bounded by the x-axis, the y-axis, x = 9, and with semi-circular crosssections x-axis.

Find the volume of the solid whose base is a circle of radius 1 centered at the origin and with isosceles right triangles crosssections x-axis.
 How to find volume of a semi circle
How to find volume of a semi circle Volumes using cross sections
Volumes using cross sections Solids with known cross sections
Solids with known cross sections Volumes of solids with known cross sections calculator
Volumes of solids with known cross sections calculator Volumes of known cross sections
Volumes of known cross sections Section 14-3 human molecular genetics
Section 14-3 human molecular genetics Euclid's method
Euclid's method Half ab sin c
Half ab sin c Finding distance with pythagorean theorem
Finding distance with pythagorean theorem Finding and using negotiation power
Finding and using negotiation power Hcf of 3 digit numbers worksheet
Hcf of 3 digit numbers worksheet Hcf from venn diagram
Hcf from venn diagram Cosine rule for obtuse angles
Cosine rule for obtuse angles Method of locating epicenter
Method of locating epicenter Area under a curve by integration
Area under a curve by integration Cutaways and cross sections definition
Cutaways and cross sections definition Cross section slice
Cross section slice Cross-section parallel
Cross-section parallel Space figures and cross sections
Space figures and cross sections Medial lateral distal proximal
Medial lateral distal proximal Wisely using resources to achieve goals is known as
Wisely using resources to achieve goals is known as Practice 10-6 volumes of pyramids and cones answers
Practice 10-6 volumes of pyramids and cones answers Mecanica respiratoria
Mecanica respiratoria Lesson 12-4 volumes of prisms and cylinders
Lesson 12-4 volumes of prisms and cylinders 11-3 reteach volume of pyramids and cones
11-3 reteach volume of pyramids and cones Practice 10-5 volumes of prisms and cylinders
Practice 10-5 volumes of prisms and cylinders Hein
Hein When administering ear drops to adults the pinna is pulled
When administering ear drops to adults the pinna is pulled Avogadro's law relationship
Avogadro's law relationship 12-6 practice surface areas and volumes of spheres answers
12-6 practice surface areas and volumes of spheres answers