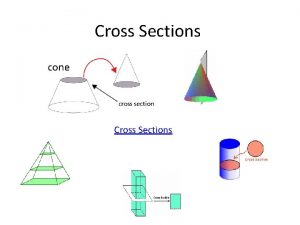
7 3 VOLUMES Solids with Known Cross Sections

7. 3 VOLUMES

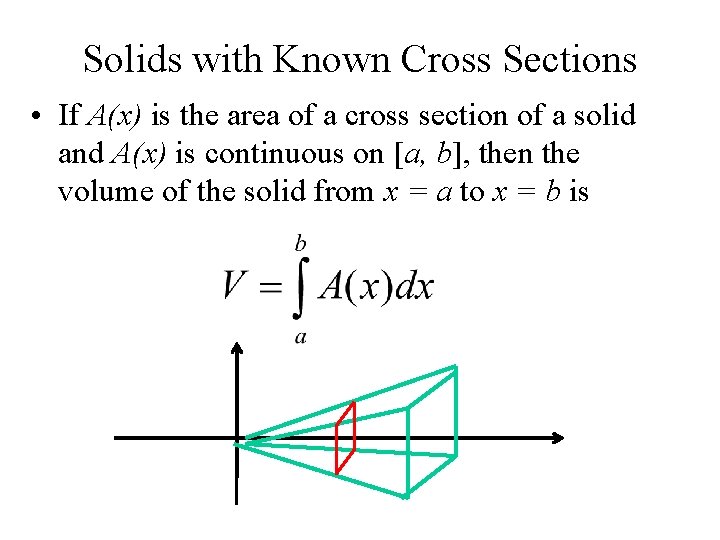
Solids with Known Cross Sections • If A(x) is the area of a cross section of a solid and A(x) is continuous on [a, b], then the volume of the solid from x = a to x = b is

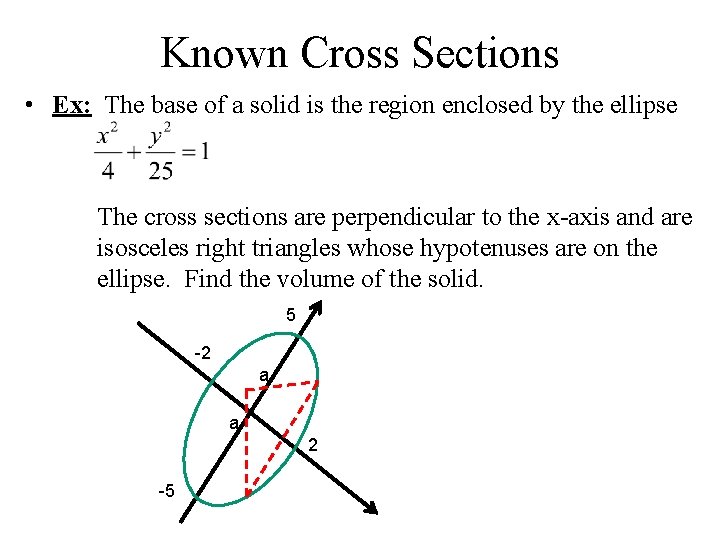
Known Cross Sections • Ex: The base of a solid is the region enclosed by the ellipse The cross sections are perpendicular to the x-axis and are isosceles right triangles whose hypotenuses are on the ellipse. Find the volume of the solid. 5 -2 a a 2 -5

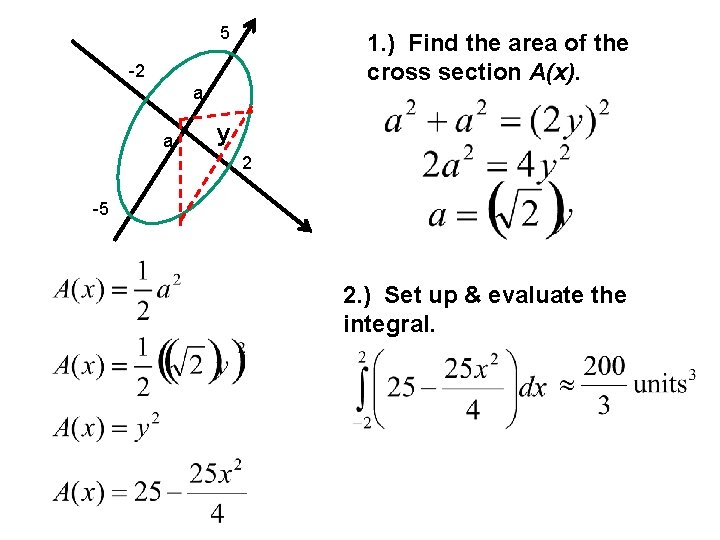
5 1. ) Find the area of the cross section A(x). -2 a a y 2 -5 2. ) Set up & evaluate the integral.

Unknown Cross Sections: DISC METHOD 1 Sketch the solid and a typical cross section. 2 Find a formula for A(x). 3 Find the limits of integration. 4 Integrate A(x) to find volume.

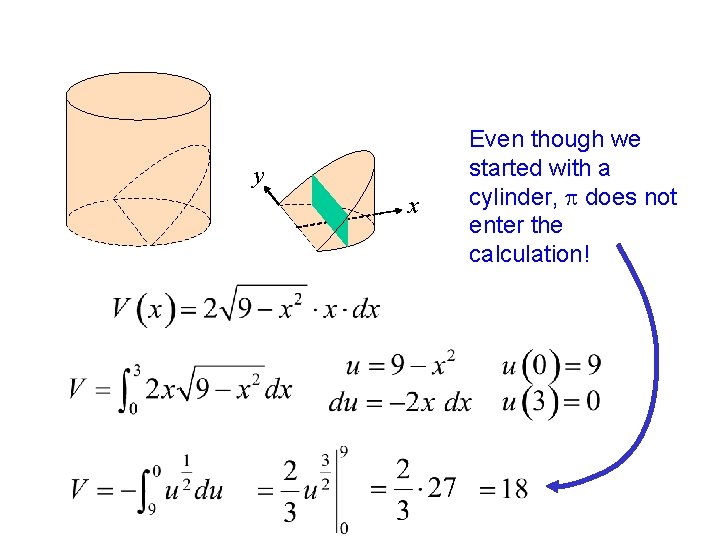
A 45 o wedge is cut from a cylinder of radius 3 as shown. Find the volume of the wedge. You could slice this wedge shape several x ways, but the simplest cross section is a rectangle. y If we let h equal the height of the slice then the volume of the slice is: Since the wedge is cut at a Since 45 o angle: 45 o x h

y x Even though we started with a cylinder, p does not enter the calculation!

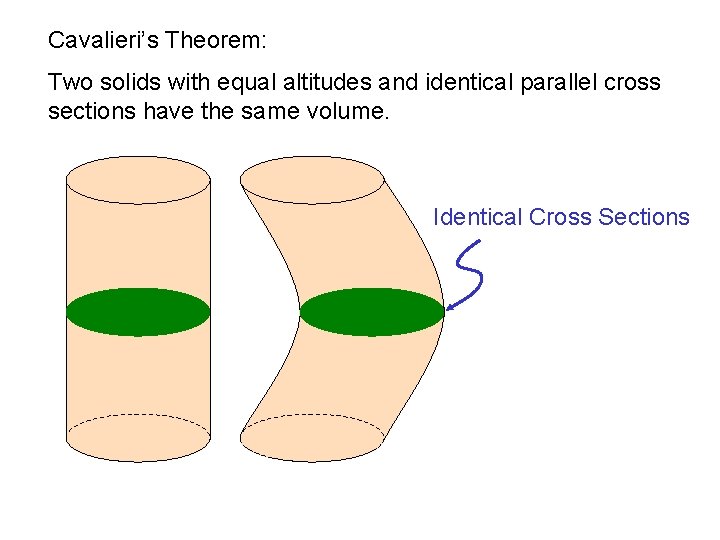
Cavalieri’s Theorem: Two solids with equal altitudes and identical parallel cross sections have the same volume. Identical Cross Sections

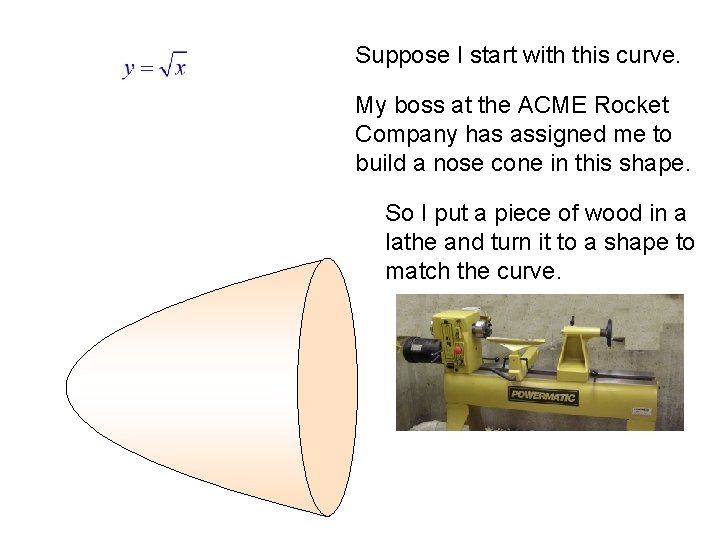
Suppose I start with this curve. My boss at the ACME Rocket Company has assigned me to build a nose cone in this shape. So I put a piece of wood in a lathe and turn it to a shape to match the curve.

How could we find the volume of the cone? One way would be to cut it into a series of thin slices (flat cylinders) and add their volumes. The volume of each flat cylinder (disk) is: In this case: r= the y value of the function thickness = a small change in x = dx

The volume of each flat cylinder (disk) is: If we add the volumes, we get:

This application of the method of slicing is called the disk method. The shape of the slice is a disk, so we use the formula for the area of a circle to find the volume of the disk. If the shape is rotated about the x-axis, then the formula is: A shape rotated about the y-axis would be: Math Demo

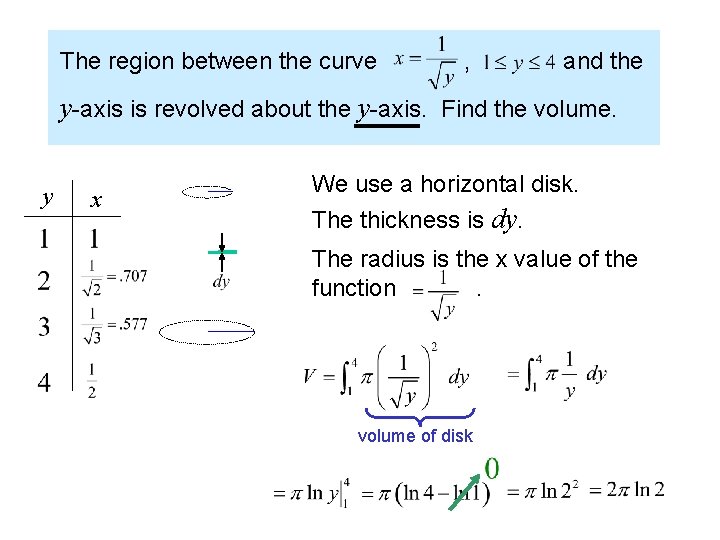
The region between the curve , and the y-axis is revolved about the y-axis. Find the volume. y x We use a horizontal disk. The thickness is dy. The radius is the x value of the function. volume of disk

The natural draft cooling tower shown at left is about 500 feet high and its shape can be approximated by the graph of this equation revolved about the y-axis: The volume can be calculated using the disk method with a horizontal disk.

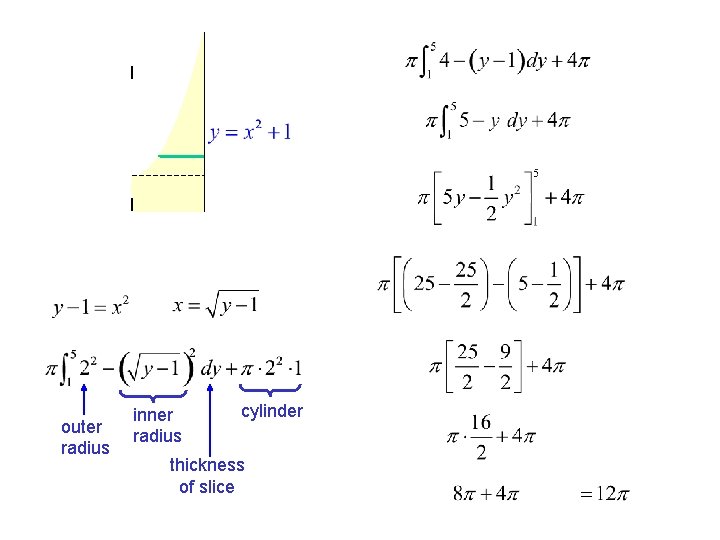
The region bounded by and is revolved about the y-axis. Find the volume. If we use a horizontal slice: The “disk” now has a hole in it, making it a “washer”. The volume of the washer is: outer radius inner radius

This application of the method of slicing is called the washer method. The shape of the slice is a circle with a hole in it, so we subtract the area of the inner circle from the area of the outer circle. The washer method formula is: Math Demo

If the same region is rotated about the line x=2: The outer radius is: r R The inner radius is:

Find the volume of the region bounded by , , and revolved about the yaxis. We can use the washer method if we split it into two parts: outer radius inner radius cylinder thickness Japanese Spider Crab of slice Georgia Aquarium, Atlanta

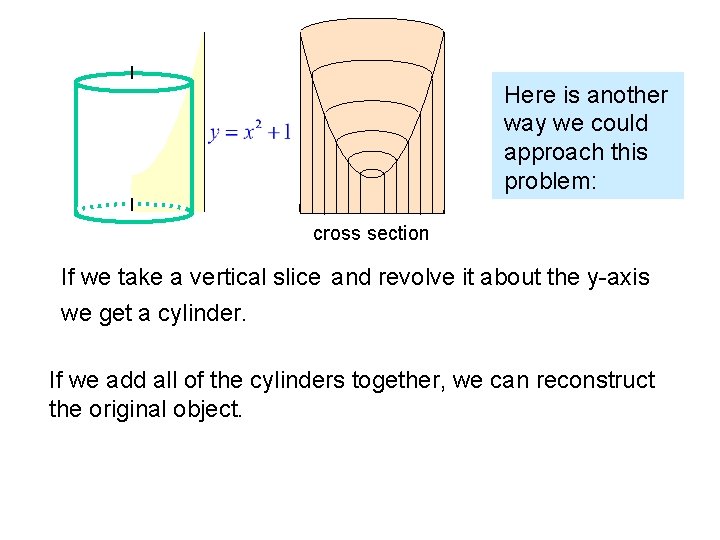
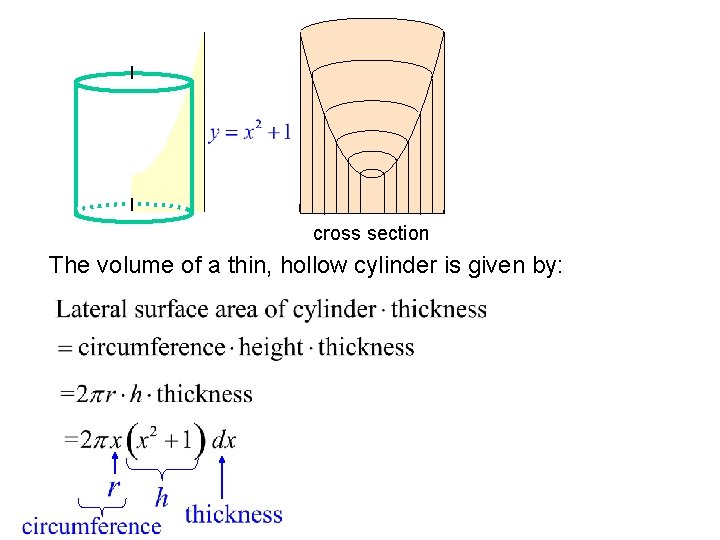
Here is another way we could approach this problem: cross section If we take a vertical slice and revolve it about the y-axis we get a cylinder. If we add all of the cylinders together, we can reconstruct the original object.

cross section The volume of a thin, hollow cylinder is given by: r is the x value of the function. h is the y value of the function. thickness is dx.

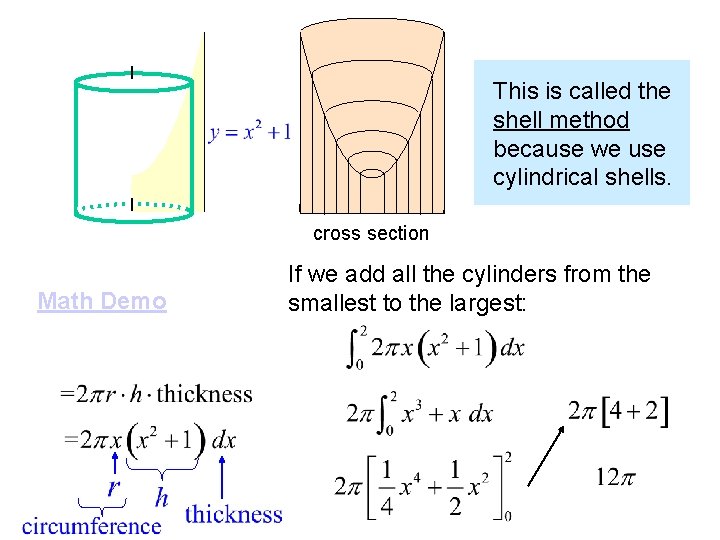
This is called the shell method because we use cylindrical shells. cross section Math Demo If we add all the cylinders from the smallest to the largest:

Find the volume generated when this shape is revolved about the y axis. We can’t solve for x, so we can’t use a horizontal slice directly.

If we take a vertical slice and revolve it about the y-axis we get a cylinder. Shell method:

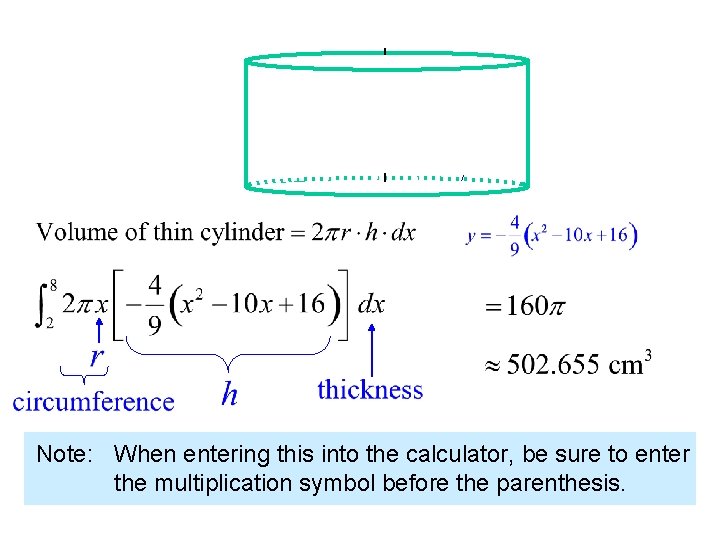
Note: When entering this into the calculator, be sure to enter the multiplication symbol before the parenthesis.

When the strip is parallel to the axis of rotation, use the shell method. When the strip is perpendicular to the axis of rotation, use the washer method.

• To find surface area, we can slice a solid and approximate the surface area of these slices by 2π ● f(x) ● Δs, where Δs is the slant height of the slice. • We will see in Section 7. 4 that Δs can be written as • To find surface area, use (SA will exist if f and f’ are continuous on [a, b]